00:00 Introduction
02:55 Le cas des délais
09:25 Délais réels (1/3)
12:13 Délais réels (2/3)
13:44 Délais réels (3/3)
16:12 L’histoire jusqu’à présent
19:31 ETA : 1 heure à partir de maintenant
22:16 CPRS (récapitulatif) (1/2)
23:44 CPRS (récapitulatif) (2/2)
24:52 Validation croisée (1/2)
27:00 Validation croisée (2/2)
27:40 Lissage des délais (1/2)
31:29 Lissage des délais (2/2)
40:51 Composition du délai (1/2)
44:19 Composition du délai (2/2)
47:52 Délai quasi-saisonnier
54:45 Modèle de délai log-logistique (1/4)
57:03 Modèle de délai log-logistique (2/4)
01:00:08 Modèle de délai log-logistique (3/4)
01:03:22 Modèle de délai log-logistique (4/4)
01:05:12 Modèle de délai incomplet (1/4)
01:08:04 Modèle de délai incomplet (2/4)
01:09:30 Modèle de délai incomplet (3/4)
01:11:38 Modèle de délai incomplet (4/4)
01:14:33 Demande sur le délai (1/3)
01:17:35 Demande sur le délai (2/3)
01:24:49 Demande sur le délai (3/3)
01:28:27 Modularité des techniques prédictives
01:31:22 Conclusion
01:32:52 Prochaine conférence et questions du public
Description
Les délais sont une facette fondamentale de la plupart des situations de supply chain. Les délais peuvent et doivent être prévus tout comme la demande. Les modèles de prévisions probabilistes, dédiés aux délais, peuvent être utilisés. Une série de techniques est présentée pour élaborer des prévisions probabilistes des délais à des fins de supply chain. La combinaison de ces prévisions, délai et demande, constitue la pierre angulaire de la modélisation prédictive en supply chain.
Transcription complète

Bienvenue dans cette série de conférences sur la supply chain. Je suis Joannes Vermorel, et aujourd’hui je vais présenter « Prévision des délais ». Les délais, et plus généralement tous les retards applicables, constituent un aspect fondamental de la supply chain lorsqu’il s’agit d’équilibrer l’offre et la demande. Il faut tenir compte des retards impliqués. Par exemple, considérons la demande pour un jouet. La bonne anticipation du pic saisonnier de la demande avant Noël n’a pas d’importance si les marchandises sont reçues en janvier. Les délais régissent les petits détails de la planification tout autant que la demande.
Les délais varient ; ils varient énormément. C’est un fait, et je vais présenter quelques preuves dans une minute. Cependant, à première vue, cette proposition est déconcertante. Il n’est pas clair pourquoi le délai devrait varier autant dès le départ. Nous avons des processus de fabrication qui peuvent fonctionner avec une tolérance de moins d’un micromètre. De plus, dans le cadre du processus de fabrication, nous pouvons contrôler un effet, par exemple l’application d’une source de lumière, jusqu’à la microseconde près. Si nous pouvons contrôler la transformation de la matière jusqu’au micromètre et à la microseconde près, avec suffisamment de rigueur, nous devrions être capables de maîtriser le flux des demandes avec un degré de précision comparable. Ou peut-être pas.
Cette façon de penser pourrait expliquer pourquoi les délais semblent si sous-estimés dans la littérature sur la supply chain. Les ouvrages sur la supply chain et, par conséquent, les logiciels de supply chain reconnaissent à peine l’existence des délais, se contentant de les introduire comme un paramètre d’entrée pour leur modèle de stocks. Pour cette conférence, il y aura trois objectifs :
Nous voulons comprendre l’importance et la nature des délais. Nous voulons comprendre comment les délais peuvent être prévus, avec un intérêt spécifique pour les modèles probabilistes qui nous permettent d’embrasser l’incertitude. Nous voulons combiner les prévisions de délais avec les prévisions de demande de manière à répondre aux besoins de la supply chain.

Selon la littérature dominante sur la supply chain, les délais ne méritent guère plus qu’une poignée de notes de bas de page. Cette affirmation pourrait sembler être une exagération extravagante, mais j’ai bien peur que ce ne soit pas le cas. Selon Google Scholar, un moteur de recherche spécialisé dans la littérature scientifique, la requête “demand forecasting” pour l’année 2021 renvoie 10 500 articles. Un coup d’œil rapide aux résultats indique qu’en effet, la grande majorité de ces publications traite de la prévision de la demande dans toutes sortes de situations et de marchés. La même requête, également pour l’année 2021, sur Google Scholar pour “lead time forecasting” renvoie 71 résultats. Les résultats pour la requête sur la prévision des délais sont si limités qu’il ne faut que quelques minutes pour parcourir toute une année de recherche.
Il s’avère qu’il n’existe qu’une dizaine d’articles qui traitent véritablement de la prévision des délais. En effet, la plupart des correspondances se trouvent dans des expressions telles que “long lead time forecast” ou “short lead time forecast” qui font référence à une prévision de la demande, et non à une prévision des délais. Il est possible de répéter cet exercice avec “demand prediction” et “lead time prediction” ainsi que d’autres expressions similaires pour d’autres années. Ces variations donnent des résultats similaires. Je laisserai cela comme exercice pour le public.
Ainsi, à titre d’estimation approximative, il existe environ mille fois plus d’articles sur la prévision de la demande que sur la prévision des délais. Les ouvrages sur la supply chain et les logiciels de supply chain suivent le même chemin, reléguant les délais au rang de citoyen de second ordre et à une technicalité insignifiante. Cependant, le personnel de supply chain présenté dans cette série de conférences nous raconte une autre histoire. Ce personnel peut représenter des entreprises fictives, mais il reflète des archétypes de la supply chain. Il nous décrit le genre de situation qui devrait être considérée comme typique. Voyons ce que ce personnel nous dit en ce qui concerne les délais.
Paris est une marque de mode fictive qui exploite son propre réseau de distribution. Paris commande auprès de fournisseurs étrangers, avec des délais longs et parfois supérieurs à six mois. Ces délais ne sont connus qu’imparfaitement, et pourtant la nouvelle collection doit arriver en magasin au moment opportun, tel que défini par l’opération marketing associée à la nouvelle collection. Les délais des fournisseurs nécessitent une anticipation adéquate ; autrement dit, ils requièrent une prévision.
Amsterdam est une entreprise FMCG fictive spécialisée dans la production de fromages, de crèmes et de beurres. Le processus d’affinage du fromage est connu et maîtrisé, mais il varie, avec des déviations de quelques jours. Pourtant, quelques jours correspondent exactement à la durée des promotions intenses déclenchées par les retail chains qui constituent le principal canal de vente d’Amsterdam. Ces délais de fabrication nécessitent une prévision.
Miami est un MRO aviation fictif. MRO signifie maintenance, réparation et révision. Chaque jetliner a besoin de milliers de pièces chaque année pour continuer à voler. Une seule pièce manquante peut immobiliser l’appareil. La durée de réparation d’une pièce réparable, également appelée TAT (turnaround time), définit le moment où la pièce redevient opérationnelle. Pourtant, le TAT varie de quelques jours à plusieurs mois, en fonction de l’ampleur des réparations, qui ne sont pas connues au moment où la pièce est retirée de l’avion. Ces TAT nécessitent une prévision.
San Jose est une entreprise de le e-commerce fictive qui distribue une variété d’articles d’ameublement et d’accessoires. Dans le cadre de son service, San Jose s’engage à fournir une date de livraison pour chaque transaction. Cependant, la livraison elle-même dépend d’entreprises tierces qui sont loin d’être parfaitement fiables. Ainsi, San Jose nécessite une estimation éclairée de la date de livraison pouvant être promise pour chaque transaction. Cette estimation éclairée constitue implicitement une prévision des délais.
Enfin, Stuttgart est une entreprise fictive du secteur aftermarket automobile. Elle exploite des succursales assurant des réparations automobiles. Le prix d’achat le plus bas pour les pièces détachées peut être obtenu auprès des grossistes qui offrent des délais longs et quelque peu irréguliers. Il existe des fournisseurs plus fiables, mais plus chers et plus proches. Choisir le bon fournisseur pour chaque pièce nécessite une analyse comparative appropriée des délais respectifs associés à divers fournisseurs.
Comme nous pouvons le constater, chacun des acteurs de la supply chain présentés jusqu’à présent nécessite l’anticipation d’au moins un délai, et souvent plusieurs. Bien que l’on puisse soutenir que la prévision de la demande requiert plus d’attention et d’efforts que la prévision des délais, au final, les deux sont nécessaires dans presque toutes les situations de supply chain.
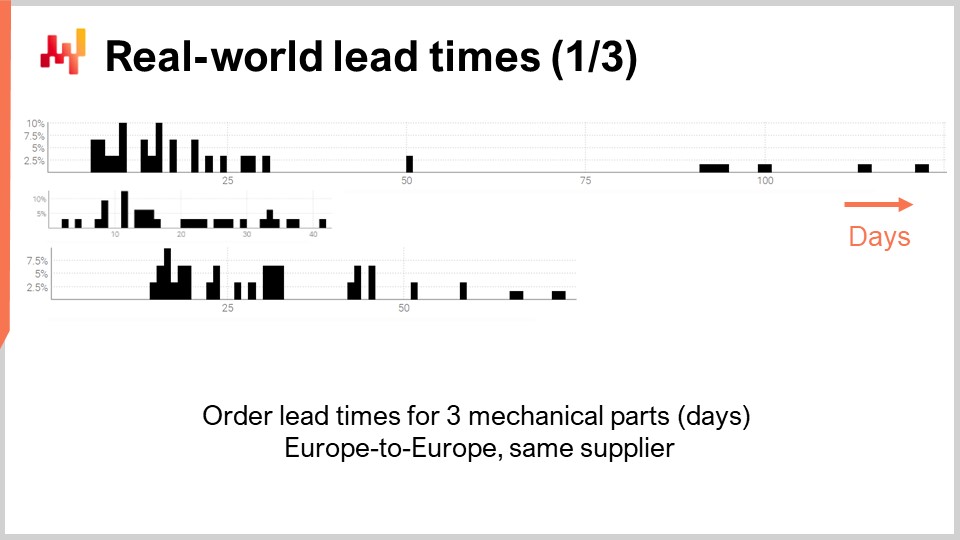
Voyons donc quelques délais réels. À l’écran se trouvent trois histogrammes qui ont été tracés en compilant les délais observés associés à trois pièces mécaniques. Ces pièces sont commandées auprès du même fournisseur situé en Europe de l’Ouest. Les commandes proviennent d’une entreprise également située en Europe de l’Ouest. L’axe des x indique la durée des délais observés exprimée en jours, et l’axe des y indique le nombre d’observations exprimé en pourcentage. Dans la suite, tous les histogrammes adopteront les mêmes conventions, avec l’axe des x associé à des durées exprimées en jours et l’axe des y reflétant la fréquence. À partir de ces trois distributions, nous pouvons déjà formuler quelques observations.
Premièrement, les données sont rares. Nous ne disposons que de quelques dizaines de points de données, et ces observations ont été collectées sur plusieurs années. Cette situation est typique ; si l’entreprise ne commande qu’une fois par mois, il faut presque une décennie pour recueillir plus de 100 observations des délais. Ainsi, quoi que nous fassions en termes de statistiques, cela doit être orienté vers de petits nombres plutôt que vers de grands nombres. En effet, nous aurons rarement le luxe de travailler avec de grands nombres.
Deuxièmement, les délais sont erratiques. Nous avons des observations allant de quelques jours à un trimestre. Bien qu’il soit toujours possible de calculer un délai moyen, se fier à une quelconque valeur moyenne pour l’une de ces pièces serait imprudent. Il est également évident qu’aucune de ces distributions n’est même vaguement normale.
Troisièmement, nous avons trois pièces qui sont quelque peu comparables en taille et en prix, et pourtant les délais varient considérablement. Bien qu’il puisse être tentant de regrouper ces observations pour rendre les données moins rares, il est évidemment imprudent de le faire, car cela reviendrait à mélanger des distributions très dissemblables. Ces distributions n’ont pas la même moyenne, ni la même médiane, ni même le même minimum ou maximum.
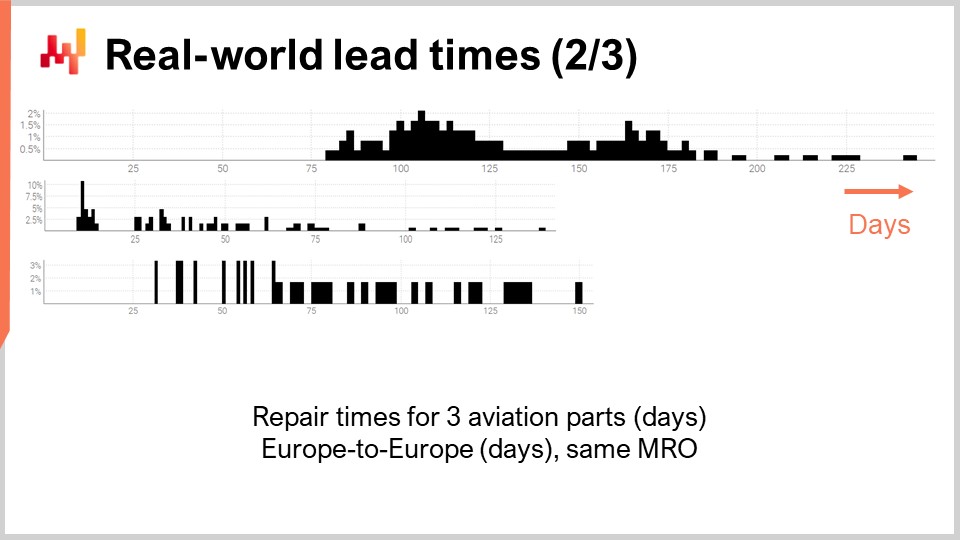
Examinons un second ensemble de délais. Ces durées reflètent le temps nécessaire pour réparer trois pièces d’avion distinctes. La première distribution semble présenter deux modes plus une queue. Lorsqu’une distribution présente deux modes, cela suggère généralement l’existence d’une variable cachée qui explique ces deux modes. Par exemple, il pourrait y avoir deux types distincts d’opérations de réparation, chaque type étant associé à son propre délai. La deuxième distribution semble présenter un mode plus une queue. Ce mode correspond à une durée relativement courte, environ deux semaines. Il pourrait refléter un processus dans lequel la pièce est d’abord inspectée, et parfois celle-ci est jugée opérationnelle sans intervention supplémentaire, d’où un délai bien plus court. La troisième distribution semble être complètement étalée, sans mode ou queue évident. Il pourrait y avoir plusieurs processus de réparation en jeu ici qui se retrouvent regroupés. La rareté des données, avec seulement trois dizaines d’observations, rend difficile d’en dire plus. Nous reviendrons sur cette troisième distribution plus tard dans cette conférence.
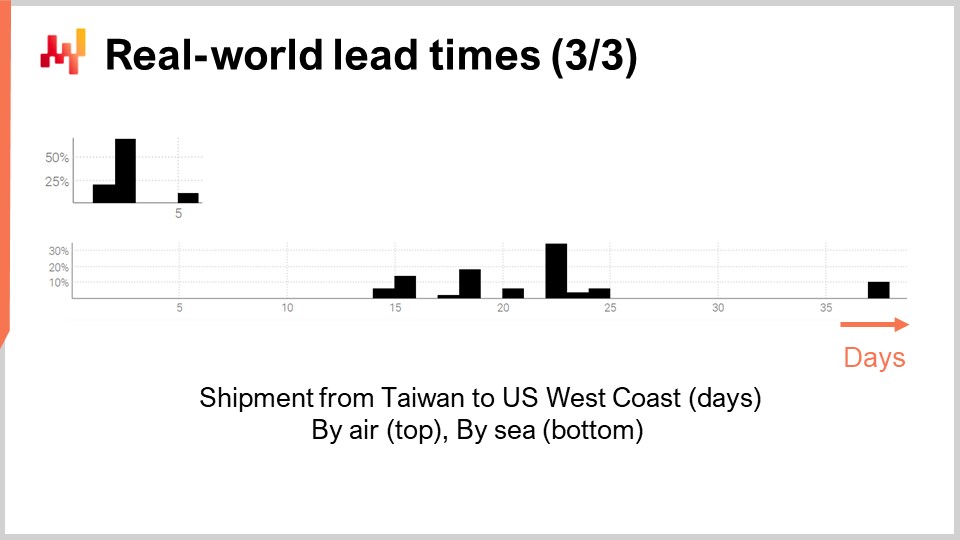
Enfin, examinons deux délais reflétant les retards d’expédition de Taïwan vers la côte ouest des États-Unis, que ce soit par avion ou par mer. Sans surprise, les avions cargos sont plus rapides que les navires de fret. La deuxième distribution semble indiquer que, parfois, une expédition maritime pourrait rater son navire initial et être expédiée avec le navire suivant, doublant presque ainsi le délai. Le même phénomène pourrait se produire avec l’expédition aérienne, bien que les données soient si limitées qu’il ne s’agisse que d’une pure supposition. Notons qu’avoir accès à seulement quelques observations n’est pas inhabituel en ce qui concerne les délais. Ces situations sont fréquentes. Il est important de garder à l’esprit que dans cette conférence, nous recherchons des outils et des instruments qui nous permettent de travailler avec les données de délai dont nous disposons, à savoir quelques observations, et non les données de délai que nous souhaiterions avoir, comme des milliers d’observations. Les courts intervalles dans les deux distributions suggèrent également l’existence d’un schéma cyclique hebdomadaire, bien que la visualisation actuelle de l’histogramme ne soit pas appropriée pour valider cette hypothèse.
De cette brève revue des délais réels, nous pouvons déjà saisir certains des phénomènes sous-jacents en jeu. En effet, les délais sont fortement structurés ; les retards ne se produisent pas sans raison, et ces causes peuvent être identifiées, décomposées et quantifiées. Cependant, les détails de la décomposition des délais ne sont souvent pas enregistrés dans les systèmes informatiques, du moins pas encore. Même lorsqu’une décomposition exhaustive du délai observé est disponible, comme cela peut être le cas dans certaines industries telles que l’aviation, cela n’implique pas que les délais puissent être parfaitement anticipés. Des sous-segments ou phases au sein du délai sont susceptibles de présenter leur propre incertitude irréductible.
Cette série de conférences sur la supply chain présente mes points de vue et mes insights tant sur l’étude que sur la pratique de la supply chain. J’essaie de garder ces conférences quelque peu indépendantes, mais elles prennent plus de sens lorsqu’elles sont regardées en séquence. Le reste de cette conférence dépend d’éléments qui ont été précédemment introduits dans cette série, bien que je fournirai un rappel dans une minute.
Le premier chapitre est une introduction générale au domaine et à l’étude de la supply chain. Il clarifie la perspective qui sous-tend cette série de conférences. Comme vous l’avez peut-être déjà deviné, cette perspective diverge substantiellement de ce qui serait considéré comme la perspective dominante sur la supply chain.
Le deuxième chapitre présente une série de méthodologies. En effet, la supply chain dépasse les méthodologies naïves. Les supply chains sont composées de personnes ayant leurs propres intérêts; il n’existe pas de partie neutre dans la supply chain. Ce chapitre aborde ces complications, y compris mon propre conflit d’intérêts en tant que CEO de Lokad, une entreprise de logiciels d’entreprise qui se spécialise dans le predictive supply chain optimization.
Le troisième chapitre passe en revue une série de “personas” de la supply chain. Ces personas sont des entreprises fictives que nous avons brièvement examinées aujourd’hui, et elles sont destinées à représenter des archétypes de situations de supply chain. Le but de ces personas est de se concentrer exclusivement sur les problèmes, en reportant la présentation des solutions.
Le quatrième chapitre passe en revue les sciences auxiliaires de la supply chain. Ces sciences ne concernent pas la supply chain en soi, mais elles doivent être considérées comme essentielles pour une pratique moderne de la supply chain. Ce chapitre inclut une progression à travers les couches d’abstraction, allant du matériel informatique jusqu’aux questions de cybersécurité.
Le cinquième et actuel chapitre est dédié à la modélisation prédictive. La modélisation prédictive est une perspective plus générale que la prévision; il ne s’agit pas seulement de prévoir la demande. Il s’agit de concevoir des modèles pouvant être utilisés pour estimer et quantifier les facteurs futurs de la supply chain d’intérêt. Aujourd’hui, nous nous penchons sur les délais, mais plus généralement dans la supply chain, tout ce qui n’est pas connu avec un degré raisonnable de certitude mérite une prévision.
Le sixième chapitre explique comment des décisions optimisées peuvent être calculées en tirant parti des modèles prédictifs, et plus spécifiquement, des modèles probabilistes qui ont été introduits dans le cinquième chapitre. Le septième chapitre revient à une perspective largement non technique afin de discuter de l’exécution réelle en entreprise d’une initiative la Supply Chain Quantitative.

Aujourd’hui, nous nous concentrons sur les délais. Nous venons de voir pourquoi les délais sont importants, et nous avons examiné une courte série de délais réels. Ainsi, nous allons aborder des éléments de modélisation des délais. Comme j’adopterai une perspective probabiliste, je vais brièvement réintroduire le Continuous Rank Probability Score (CRPS), une métrique permettant d’évaluer la qualité d’une prévision probabiliste. J’introduirai également cross-validation et une variante de la cross-validation adaptée à notre perspective probabiliste. Munis de ces outils, nous présenterons et évaluerons notre premier modèle probabiliste non naïf pour les délais. Les données sur les délais sont rares, et le premier point à l’ordre du jour est de lisser ces distributions. Les délais peuvent être décomposés en une série de phases intermédiaires. Ainsi, en supposant que certaines données de délais décomposés soient disponibles, nous avons besoin de quelque chose pour recomposer ces délais tout en préservant l’angle probabiliste.
Ensuite, nous allons réintroduire le differentiable programming. Le differentiable programming a déjà été utilisé dans cette série de conférences pour prévoir la demande, mais il peut également être utilisé pour prévoir les délais. Nous le ferons en commençant par un exemple simple destiné à capturer l’impact du Nouvel An chinois sur les délais, un schéma typique observé lors de l’importation de marchandises depuis l’Asie.
Nous poursuivrons ensuite avec un modèle probabiliste paramétrique pour les délais, en tirant parti de la distribution log-logistique. Encore une fois, le differentiable programming sera instrumental pour apprendre les paramètres du modèle. Nous étendrons ensuite ce modèle en considérant des observations de délais incomplètes. En effet, même les bons de commande qui ne sont pas encore finalisés nous fournissent une certaine information sur les délais.
Enfin, nous réunissons une prévision probabiliste des délais et une prévision probabiliste de la demande au sein d’une situation unique de stocks replenishment. Cela sera l’occasion de démontrer pourquoi la modularité est une préoccupation essentielle en matière de modélisation prédictive, plus encore que les détails des modèles eux-mêmes.

Dans la conférence 5.2 sur la prévision probabiliste, nous avons déjà présenté quelques outils pour évaluer la qualité d’une prévision probabiliste. En effet, les métriques de précision habituelles, telles que l’erreur quadratique moyenne ou l’erreur absolue moyenne, ne s’appliquent qu’aux prévisions ponctuelles, et non aux prévisions probabilistes. Pourtant, ce n’est pas parce que nos prévisions deviennent probabilistes que la notion d’exactitude, au sens général, perd de sa pertinence. Nous avons simplement besoin d’un instrument statistique compatible avec la perspective probabiliste.
Parmi ces instruments, il y a le Continuous Rank Probability Score (CRPS). La formule est affichée à l’écran. Le CRPS est une généralisation de la métrique L1, c’est-à-dire de l’erreur absolue, mais pour les distributions de probabilité. La version habituelle du CRPS compare une distribution, nommée F ici, à une observation, nommée X ici. La valeur obtenue grâce à la fonction CRPS est homogène par rapport à l’observation. Par exemple, si X est un délai exprimé en jours, alors la valeur du CRPS est également exprimée en jours.

Le CRPS peut être généralisé pour comparer deux distributions. C’est ce qui est montré à l’écran. Il s’agit simplement d’une variation mineure de la formule précédente. L’essence de cette métrique reste inchangée. Si F est la réelle distribution des délais et F_hat est une estimation de la distribution des délais, alors le CRPS est exprimé en jours. Le CRPS reflète l’ampleur de la différence entre les deux distributions. Il peut également être interprété comme la quantité minimale d’énergie nécessaire pour transporter toute la masse de la première distribution afin qu’elle prenne exactement la forme de la deuxième distribution.
Nous disposons désormais d’un instrument pour comparer deux distributions de probabilité unidimensionnelles. Cela deviendra intéressant dans un instant, lorsque nous présenterons notre premier modèle probabiliste pour les délais.
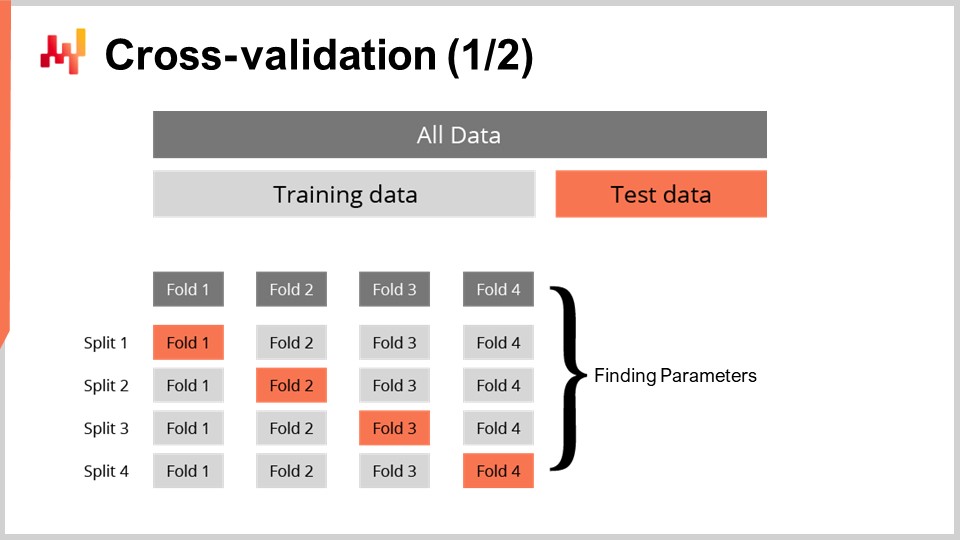
Disposer d’une métrique pour mesurer la qualité d’une prévision probabiliste n’est pas suffisant. La métrique mesure la qualité sur les données dont nous disposons; cependant, ce que nous voulons réellement, c’est être capables d’évaluer la qualité de notre prévision sur des données que nous ne possédons pas. En effet, ce sont les délais futurs qui nous intéressent, et non ceux qui ont déjà été observés dans le passé. Notre capacité à faire en sorte qu’un modèle performe bien sur des données que nous n’avons pas se nomme généralisation. La cross-validation est une technique générale de validation de modèle, précisément destinée à évaluer la capacité d’un modèle à bien généraliser.
Dans sa forme la plus simple, la cross-validation consiste à partitionner les observations en un petit nombre de sous-ensembles. Pour chaque itération, un sous-ensemble est mis de côté et désigné comme le sous-ensemble de test. Le modèle est ensuite généré ou entraîné à partir des autres sous-ensembles de données, appelés sous-ensembles d’entraînement. Après l’entraînement, le modèle est validé sur le sous-ensemble de test. Ce processus est répété un certain nombre de fois, et la qualité moyenne obtenue sur l’ensemble des itérations représente le résultat final de la cross-validation.
La cross-validation est rarement utilisée dans le contexte de la prévision des séries temporelles en raison de la dépendance temporelle entre les observations. En effet, la cross-validation, telle que présentée, suppose que les observations sont indépendantes. Lorsque des séries temporelles sont impliquées, on utilise le backtesting à la place. Le backtesting peut être considéré comme une forme de cross-validation qui prend en compte la dépendance temporelle.
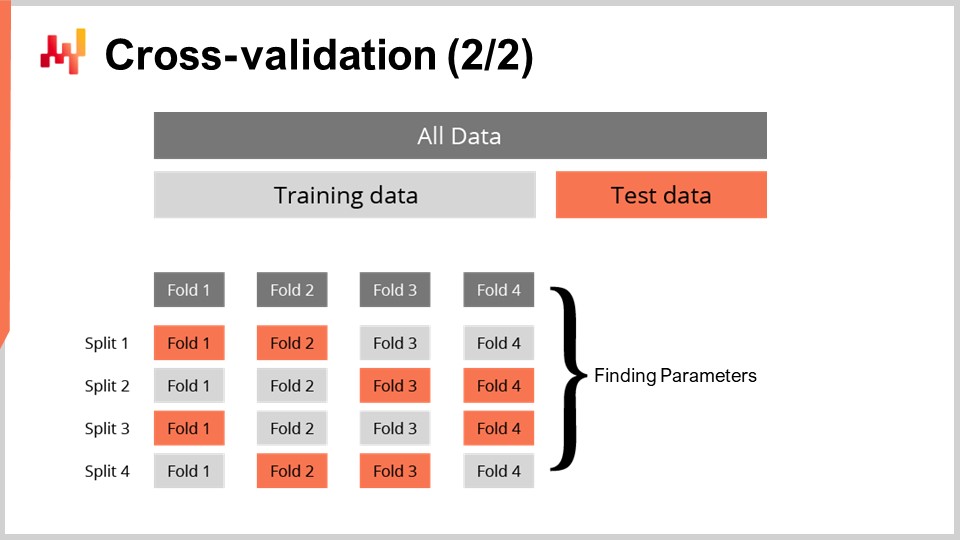
La technique de cross-validation comporte de nombreuses variantes qui reflètent un vaste éventail d’angles potentiels susceptibles d’être abordés. Nous ne passerons pas en revue ces variantes dans le cadre de cette conférence. J’utiliserai une variante spécifique où, à chaque séparation, le sous-ensemble d’entraînement et le sous-ensemble de test ont à peu près la même taille. Cette variante a été introduite pour traiter la validation d’un modèle probabiliste, comme nous le verrons avec un peu de code dans un instant.
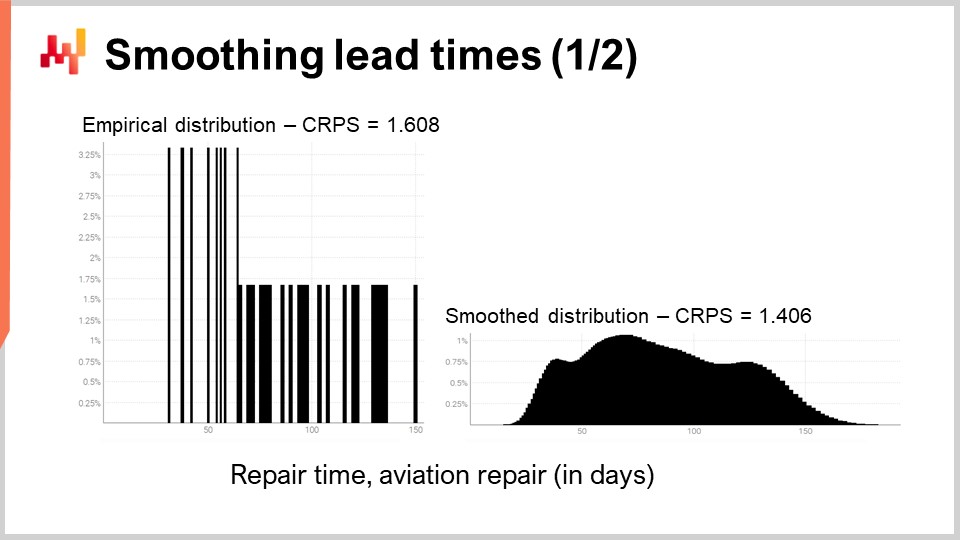
Revisitons l’un des délais réels que nous avons vus précédemment à l’écran. À gauche, l’histogramme est associé aux distributions des temps de réparation aéronautique tierces. Ce sont les mêmes observations que celles déjà vues, et l’histogramme a simplement été étiré verticalement. Ce faisant, les deux histogrammes, à gauche et à droite, partagent la même échelle. Pour l’histogramme de gauche, nous avons environ 30 observations. Ce n’est pas beaucoup, mais c’est déjà plus que ce que nous aurons fréquemment.
L’histogramme de gauche est appelé une distribution empirique. Il s’agit littéralement de l’histogramme brut tel qu’obtenu à partir des observations. L’histogramme comporte un compartiment pour chaque durée exprimée en nombre entier de jours. Pour chaque compartiment, nous comptons le nombre de délais observés. En raison de la rareté des données, la distribution empirique ressemble à un code-barres.
Il y a un problème ici. Si nous avons deux délais observés exactement à 50 jours, est-il logique de dire que la probabilité d’observer soit 49 jours, soit 51 jours, est exactement nulle ? Ce n’est pas le cas. Clairement, il existe un spectre de durées; nous n’avons tout simplement pas assez de points de données pour observer la véritable distribution sous-jacente, qui est très probablement bien plus lisse que cette distribution semblable à un code-barres.
Ainsi, lorsqu’il s’agit de lisser cette distribution, il existe une infinité de manières d’effectuer cette opération de lissage. Certaines méthodes de lissage peuvent sembler efficaces, mais ne sont pas statistiquement fondées. Comme point de départ, nous souhaitons nous assurer qu’un modèle lissé soit plus précis que le modèle empirique. Il s’avère que nous avons déjà présenté deux instruments, le CRPS et la cross-validation, qui nous permettront de le faire.
Dans un instant, les résultats seront affichés. L’erreur CRPS associée à la distribution en code-barres est de 1,6 jour, tandis que l’erreur CRPS associée à la distribution lissée est de 1,4 jour. Ces deux valeurs ont été obtenues grâce à la cross-validation. L’erreur plus faible indique que, au sens du CRPS, la distribution de droite est la plus précise des deux. La différence de 0,2 entre 1,4 et 1,6 n’est pas énorme; cependant, la caractéristique essentielle ici est que nous disposons d’une distribution lissée qui ne laisse pas de manière erratique certaines durées intermédiaires avec une probabilité nulle. Cela est raisonnable, car notre compréhension des réparations nous indique que ces durées se produiraient très probablement si les réparations étaient répétées. Le CRPS ne reflète pas la véritable ampleur de l’amélioration apportée par le lissage de la distribution. Cependant, au moins, la baisse du CRPS confirme que cette transformation est raisonnable d’un point de vue statistique.
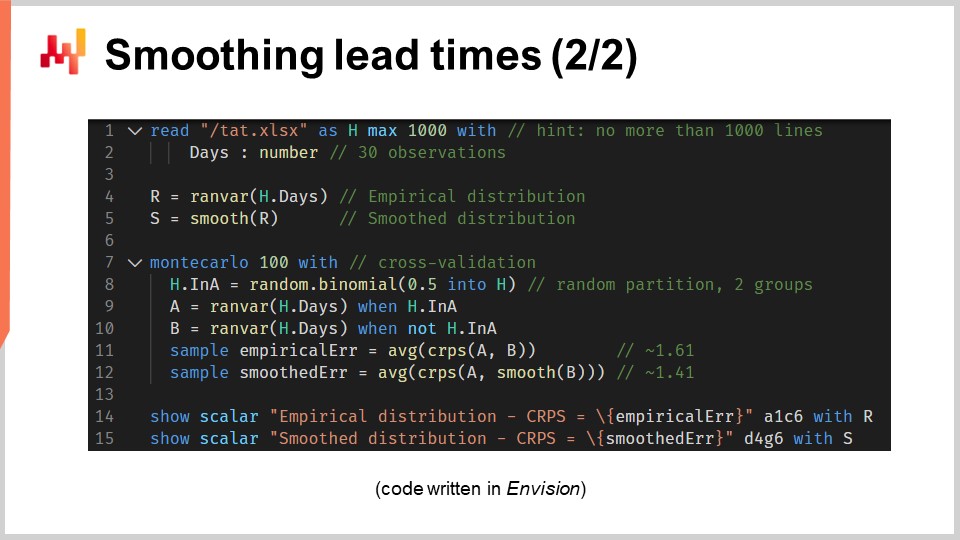
Voyons maintenant le code source qui a produit ces deux modèles et affiché ces deux histogrammes. En tout, cela est réalisé en 12 lignes de code si l’on exclut les lignes blanches. Comme d’habitude dans cette série de conférences, le code est écrit en Envision, le langage de programmation spécifique à Lokad dédié à l’optimisation prédictive des supply chains. Cependant, il n’y a pas de magie; cette logique aurait pu être écrite en Python. Mais pour le type de problèmes que nous abordons dans cette conférence, Envision est plus concis et plus autonome.
Repassons en revue ces 12 lignes de code. Aux lignes 1 et 2, nous lisons un tableur Excel qui comporte une seule colonne de données. Le tableur contient 30 observations. Ces données sont rassemblées dans une table nommée “H” qui possède une seule colonne nommée “days”. À la ligne 4, nous construisons une distribution empirique. La variable “R” a pour type de donnée “ranvar”, et sur le côté droit de l’affectation, la fonction “ranvar” est un agrégateur qui prend des observations en entrée et renvoie l’histogramme représenté avec un type de donnée “ranvar”. En conséquence, le type de donnée “ranvar” est dédié aux distributions entières unidimensionnelles. Nous avons introduit le type de donnée “ranvar” dans une conférence précédente de ce chapitre. Ce type de donnée garantit une empreinte mémoire constante et un temps de calcul constant pour chaque opération. L’inconvénient du “ranvar” en tant que type de donnée est qu’une compression avec perte est impliquée, bien que la perte de données causée par cette compression ait été conçue pour être sans conséquence pour les besoins de la supply chain.
À la ligne 5, nous lissons la distribution avec la fonction intégrée nommée “smooth”. En interne, cette fonction remplace la distribution originale par un mélange de distributions de Poisson. Chaque compartiment de l’histogramme est transformé en une distribution de Poisson ayant pour moyenne la position entière du compartiment, et enfin, le mélange attribue à chaque distribution de Poisson un poids proportionnel à celui du compartiment lui-même. Une autre manière de comprendre ce que fait la fonction “smooth” est de considérer qu’elle équivaut à remplacer chaque observation par une distribution de Poisson dont la moyenne est égale à l’observation elle-même. Toutes ces distributions de Poisson, une par observation, sont ensuite mélangées. Le mélange signifie la moyenne des valeurs respectives des compartiments de l’histogramme. Les variables “ranvar” “R” et “S” ne seront plus utilisées avant les lignes 14 et 15, où elles seront affichées.
À la ligne 7, nous démarrons un bloc Monte Carlo. Ce bloc est une sorte de boucle, et il va être exécuté 100 fois, comme spécifié par les 100 valeurs qui apparaissent juste après le mot-clé Monte Carlo. Le bloc Monte Carlo est destiné à collecter des observations indépendantes générées selon un processus impliquant un certain degré de hasard. Vous vous demandez peut-être pourquoi il existe une construction spécifique Monte Carlo dans Envision au lieu d’utiliser simplement une boucle, comme c’est généralement le cas dans les langages de programmation classiques. Il s’avère qu’avoir une construction dédiée offre des avantages substantiels. Premièrement, cela garantit que les itérations sont véritablement indépendantes, jusqu’aux graines utilisées pour générer le pseudo-aléatoire. Deuxièmement, cela offre une cible explicite pour la distribution automatisée de la charge de travail sur plusieurs cœurs CPU ou même sur plusieurs machines.
À la ligne 8, nous créons un vecteur aléatoire de valeurs booléennes dans la table “H”. Avec cette ligne, nous créons des valeurs aléatoires indépendantes, appelées déviations (true ou false), pour chaque ligne de la table “H”. Comme d’habitude avec Envision, les boucles sont abstraites grâce à la programmation par tableau. Avec ces valeurs booléennes, nous partitionnons la table “H” en deux groupes. Cette répartition aléatoire est utilisée pour le processus de validation croisée.
Aux lignes 9 et 10, nous créons deux “ranvars” nommés “A” et “B”, respectivement. Nous utilisons à nouveau l’agrégateur “ranvar”, mais cette fois-ci, nous appliquons un filtre avec le mot-clé “when” juste après l’appel à l’agrégateur. “A” est généré en utilisant uniquement les lignes où la valeur dans “a” est true ; pour “B”, c’est l’inverse. “B” est généré en utilisant uniquement les lignes où la valeur dans “a” est false.
Aux lignes 11 et 12, nous collectons les chiffres d’intérêt du bloc Monte Carlo. Dans Envision, le mot-clé “sample” ne peut être placé qu’à l’intérieur d’un bloc Monte Carlo. Il est utilisé pour collecter les observations effectuées lors de multiples itérations du processus Monte Carlo. À la ligne 11, nous calculons l’erreur moyenne, exprimée en termes de CRPS, entre deux distributions empiriques : un sous-échantillon issu de l’ensemble original des lead times. Le mot-clé “sample” spécifie que les valeurs sont collectées au cours des itérations Monte Carlo. L’agrégateur “AVG”, qui signifie “average” sur le côté droit de l’assignation, est utilisé pour produire une seule estimation à la fin du bloc.
À la ligne 12, nous faisons quelque chose d’assez similaire à ce qui s’est passé à la ligne 11. Cette fois-ci, toutefois, nous appliquons la fonction “smooth” au “ranvar” “B”. Nous voulons évaluer à quel point la variante lissée se rapproche de la distribution empirique naïve. Il s’avère qu’elle est plus proche, du moins en termes de CRPS, que ses homologues empiriques originaux.
Aux lignes 14 et 15, nous affichons les histogrammes et les valeurs de CRPS. Ces lignes génèrent les figures que nous avons vues dans la diapositive précédente. Ce script nous fournit notre ligne de base pour la qualité de la distribution empirique de notre modèle. En effet, bien que ce modèle, le modèle “barcode”, soit sans doute naïf, il reste un modèle, et de surcroît un modèle probabiliste. Ainsi, ce script nous fournit également un meilleur modèle, du moins au sens du CRPS, grâce à une variante lissée de la distribution empirique originale.
Pour l’instant, selon votre familiarité avec les langages de programmation, cela peut sembler beaucoup à assimiler. Cependant, je tiens à souligner à quel point il est simple de produire une distribution de probabilité raisonnable, même lorsque nous n’avons que quelques observations. Bien que nous ayons 12 lignes de code, seules les lignes 4 et 5 représentent la véritable partie de modélisation de l’exercice. Si nous n’étions intéressés que par la variante lissée, alors le “ranvar” “S” pourrait être écrit en une seule ligne de code. Ainsi, c’est littéralement une ligne de code : d’abord, appliquer une agrégation ranvar, puis appliquer un opérateur de lissage, et nous avons terminé. Le reste n’est que de l’instrumentation et de l’affichage. Avec les outils appropriés, la modélisation probabiliste, que ce soit le lead time ou autre, peut être rendue extrêmement simple. Il n’y a pas de grande mathématique impliquée, ni de grand algorithme, ni de grands morceaux de logiciel. C’est simple et remarquablement ainsi.

Comment obtenir un envoi avec un retard de six mois ? La réponse est évidente : un jour à la fois. Plus sérieusement, les lead times peuvent généralement être décomposés en une série de retards. Par exemple, un supplier lead time peut être décomposé en un délai d’attente lorsque la commande est mise dans une file d’attente, suivi d’un délai de fabrication pendant lequel les marchandises sont produites, et enfin suivi d’un délai de transit lorsque les marchandises sont expédiées. Ainsi, si les lead times peuvent être décomposés, il est également intéressant de pouvoir les recomposer.
Si nous vivions dans un monde hautement déterministe où l’avenir pourrait être anticipé précisément, alors recomposer les lead times ne serait qu’une question d’addition. En revenant à l’exemple que je viens de mentionner, composer le délai de commande serait la somme du délai de file d’attente en jours, du délai de fabrication en jours, et du délai de transit en jours. Pourtant, nous ne vivons pas dans un monde où l’avenir peut être anticipé précisément. Les distributions des lead times réels que nous avons présentées au début de cette conférence soutiennent cette affirmation. Les lead times sont erratiques, et il y a peu de raison de croire que cela changera fondamentalement dans les décennies à venir.
Ainsi, les futurs lead times doivent être appréhendés comme des variables aléatoires. Ces variables aléatoires intègrent et quantifient l’incertitude au lieu de l’ignorer. Plus précisément, cela signifie que chaque composant du lead time doit également être modélisé individuellement comme une variable aléatoire. En revenant à notre exemple, le délai de commande est une variable aléatoire, et il est obtenu comme la somme de trois variables aléatoires respectivement associées au délai de file d’attente, au délai de fabrication et au délai de transit.
La formule pour la somme de deux variables aléatoires indépendantes, unidimensionnelles et à valeurs entières est présentée à l’écran. Cette formule indique simplement que si nous obtenons une durée totale de Z jours, et si nous avons K jours pour la première variable aléatoire X, alors nous devons avoir Z moins K jours pour la seconde variable aléatoire Y. Ce type d’addition est généralement connu en mathématiques sous le nom de convolutions.
Bien qu’il semble y avoir un nombre infini de termes dans cette convolution, en pratique, nous ne nous intéressons qu’à un nombre fini de termes. Premièrement, toutes les durées négatives ont une probabilité nulle ; en effet, des retards négatifs signifieraient voyager dans le temps. Deuxièmement, pour des retards importants, les probabilités deviennent si faibles que, pour des besoins pratiques de supply chain, elles peuvent être approximées de manière fiable par zéro.
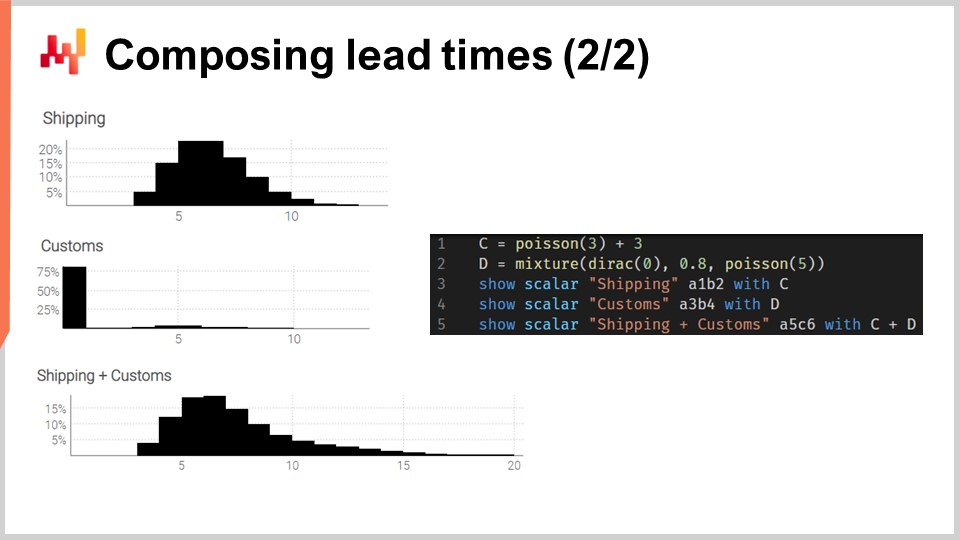
Mettons ces convolutions en pratique. Considérons un transit time qui peut être décomposé en deux phases : un retard d’expédition suivi d’un retard de dédouanement. Nous voulons modéliser ces deux phases avec deux variables aléatoires indépendantes, puis recomposer le transit time en additionnant ces deux variables aléatoires.
À l’écran, les histogrammes à gauche sont produits par le script à droite. À la ligne 1, le retard d’expédition est modélisé comme une convolution d’une distribution de Poisson plus une constante. La fonction Poisson retourne un type de données “ranvar” ; ajouter trois a pour effet de décaler la distribution vers la droite. Le “ranvar” résultant est assigné à la variable “C”. Ce “ranvar” est affiché à la ligne 3. On peut le voir à gauche comme l’histogramme le plus en haut. Nous reconnaissons la forme d’une distribution de Poisson qui a été décalée vers la droite de quelques unités, trois unités dans ce cas. À la ligne 2, le dédouanement est modélisé comme un mélange d’un Dirac à zéro et d’un Poisson à cinq. Le Dirac à zéro se produit quatre-vingt pour cent du temps ; c’est ce que signifie cette constante 0.8. Cela reflète des situations où, la plupart du temps, les marchandises ne sont même pas inspectées par la douane et passent sans retard notable. Alternativement, vingt pour cent du temps, les marchandises sont inspectées par la douane, et le retard est modélisé comme une distribution de Poisson avec une moyenne de cinq. Le ranvar résultant est assigné à une variable nommée D. Ce ranvar est affiché à la ligne 4 et peut être vu à gauche comme l’histogramme du milieu. Cet aspect asymétrique reflète que, la plupart du temps, la douane n’ajoute aucun retard.
Enfin, à la ligne 5, nous calculons C plus D. Cette addition est une convolution, puisque C et D sont tous deux des ranvars, et non des nombres. Il s’agit de la deuxième convolution dans ce script, une convolution ayant déjà eu lieu à la ligne 1. Le ranvar résultant est affiché et est visible à gauche comme le troisième histogramme, le plus bas. Ce troisième histogramme est similaire au premier, sauf que la queue s’étend beaucoup plus à droite. Une fois de plus, nous constatons qu’avec quelques lignes de code, nous pouvons aborder des effets réels non triviaux, tels que les retards de dédouanement à la douane.
Cependant, deux critiques pourraient être formulées à propos de cet exemple. Premièrement, il n’est pas indiqué d’où proviennent les constantes ; en pratique, nous souhaitons apprendre ces constantes à partir des données historiques. Deuxièmement, bien que la distribution de Poisson ait l’avantage de la simplicité, elle pourrait ne pas être une forme très réaliste pour la modélisation des lead times, surtout en considérant des situations de fat-tail. Ainsi, nous allons aborder ces deux points dans l’ordre.
Pour apprendre des paramètres à partir des données, nous allons revisiter un paradigme de programmation que nous avons déjà introduit dans cette série de conférences, à savoir la programmation différentiable. Si vous n’avez pas visionné les conférences précédentes dans ce chapitre, je vous invite à les consulter après la fin de la présente conférence. La programmation différentiable est présentée plus en détail dans ces conférences.
La programmation différentiable est une combinaison de deux techniques : la descente de gradient stochastique et la différentiation automatique. La descente de gradient stochastique est une technique d’optimisation qui ajuste les paramètres, une observation à la fois, dans la direction opposée aux gradients. La différentiation automatique est une technique de compilation, comme dans le compilateur d’un langage de programmation, qui calcule les gradients pour tous les paramètres apparaissant dans un programme général.
Illustrons la programmation différentiable avec un problème de lead time. Cela servira soit de révision, soit d’introduction, selon votre familiarité avec ce paradigme. Nous voulons modéliser l’impact du Nouvel An chinois sur les lead times associés aux importations de Chine. En effet, alors que les usines ferment pendant deux ou trois semaines pour le Nouvel An chinois, les lead times s’allongent. Le Nouvel An chinois est cyclique ; il a lieu chaque année. Toutefois, il n’est pas strictement saisonnier, du moins pas au sens du calendrier grégorien.
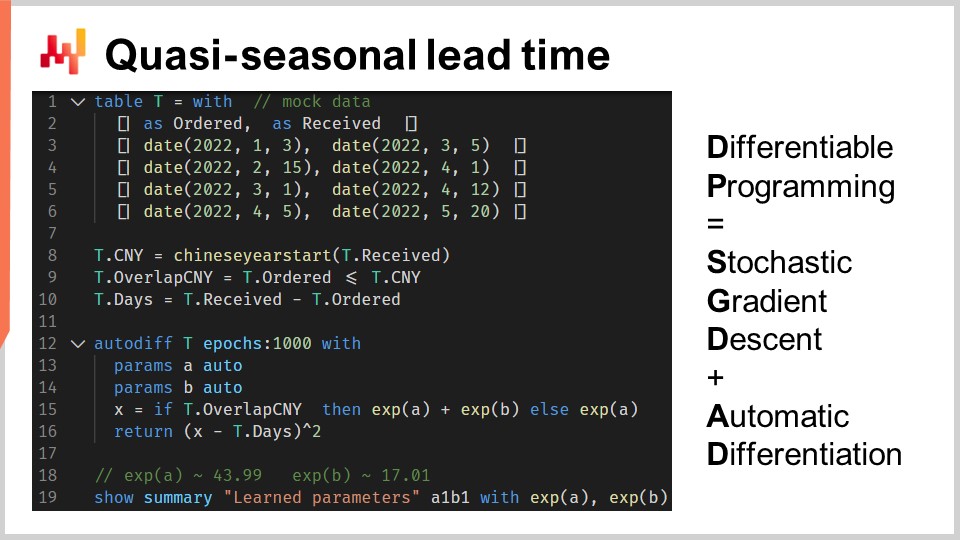
Aux lignes un à six, nous introduisons quelques commandes fictives avec quatre observations, comportant à la fois une date de commande et une date de réception. En pratique, ces données ne seraient pas codées en dur, mais nous chargerions ces données historiques depuis les systèmes de l’entreprise. Aux lignes huit et neuf, nous calculons si le lead time recouvre le Nouvel An chinois ou non. La variable “T.overlap_CNY” est un vecteur booléen ; elle indique si l’observation est impactée par le Nouvel An chinois ou non.
À la ligne 12, nous introduisons un bloc “autodiff”. La table T est utilisée comme table d’observation, et il y a 1000 époques. Cela signifie que chaque observation, donc chaque ligne de la table T, sera visitée mille fois. Une étape de la descente de gradient stochastique correspond à une exécution de la logique à l’intérieur du bloc “autodiff”.
Aux lignes 13 et 14, deux paramètres scalaires sont déclarés. Le bloc “autodiff” apprendra ces paramètres. Le paramètre A reflète le lead time de base sans l’effet du Nouvel An chinois, et le paramètre B reflète le retard supplémentaire associé au Nouvel An chinois. À la ligne 15, nous calculons X, la prédiction de lead time de notre modèle. Il s’agit d’un modèle déterministe, et non probabiliste ; X est une prévision ponctuelle du lead time. La partie droite de l’assignation est simple : si l’observation recouvre le Nouvel An chinois, alors nous renvoyons le lead time de base plus la composante Nouvel An ; sinon, nous renvoyons uniquement le lead time de base. Comme le bloc “autodiff” prend une seule observation à la fois, à la ligne 15, la variable T.overlap_CNY fait référence à une valeur scalaire et non à un vecteur. Cette valeur correspond à la ligne choisie comme ligne d’observation dans la table T.
Les paramètres A et B sont enveloppés dans la fonction exponentielle “exp”, ce qui constitue une petite astuce de programmation différentiable. En effet, l’algorithme qui pilote la descente de gradient stochastique tend à être relativement conservateur en ce qui concerne les variations incrémentales des paramètres. Ainsi, si nous souhaitons apprendre un paramètre positif qui pourrait dépasser, disons, 10, alors envelopper ce paramètre dans un processus exponentiel accélère la convergence.
À la ligne 16, nous renvoyons une erreur quadratique moyenne entre notre prédiction X et la durée observée, exprimée en jours (T.days). Encore une fois, à l’intérieur de ce bloc “autodiff”, T.days est une valeur scalaire et non un vecteur. Comme la table T est utilisée comme table d’observation, la valeur de retour est traitée comme la perte qui est minimisée par la descente de gradient stochastique. La différentiation automatique propage les gradients de la perte vers les paramètres A et B. Enfin, à la ligne 19, nous affichons les deux valeurs que nous avons apprises, respectivement pour A et B, qui représentent le lead time de base et la composante Nouvel An de notre lead time.
Cela conclut notre réintroduction de la programmation différentiable en tant qu’outil polyvalent permettant d’apprendre des patterns statistiques. À partir d’ici, nous reviendrons sur les blocs “autodiff” avec des situations plus élaborées. Cependant, rappelons une fois de plus que, même s’il peut sembler un peu écrasant, rien de vraiment compliqué ne se passe ici. Sans doute, le morceau de code le plus complexe de ce script est l’implémentation sous-jacente de la fonction “ChineseYearStart”, appelée à la ligne huit, qui fait partie de la bibliothèque standard d’Envision. En quelques lignes de code, nous introduisons un modèle avec deux paramètres et apprenons ces paramètres. Là encore, cette simplicité est remarquable.
Les lead times sont fréquemment à queue épaisse ; c’est-à-dire que, lorsqu’un lead time dévie, il dévie énormément. Ainsi, afin de modéliser le lead time, il est intéressant d’adopter des distributions capables de reproduire ces comportements à queue épaisse. La littérature mathématique présente une vaste liste de telles distributions, et pas mal d’entre elles conviendraient à notre objectif. Cependant, passer en revue l’ensemble du panorama mathématique nous prendrait des heures. Notons simplement que la distribution de Poisson n’a pas de queue épaisse. Ainsi, aujourd’hui, je vais choisir la distribution log-logistique, qui se trouve être une distribution à queue épaisse. La justification principale de ce choix est que les équipes de Lokad modélisent les lead times à l’aide de distributions log-logistiques pour plusieurs clients. Elle fonctionne remarquablement bien avec un minimum de complications. Gardons toutefois à l’esprit que la distribution log-logistique n’est en aucun cas une solution miracle, et il existe de nombreuses situations où Lokad modélise différemment les lead times.
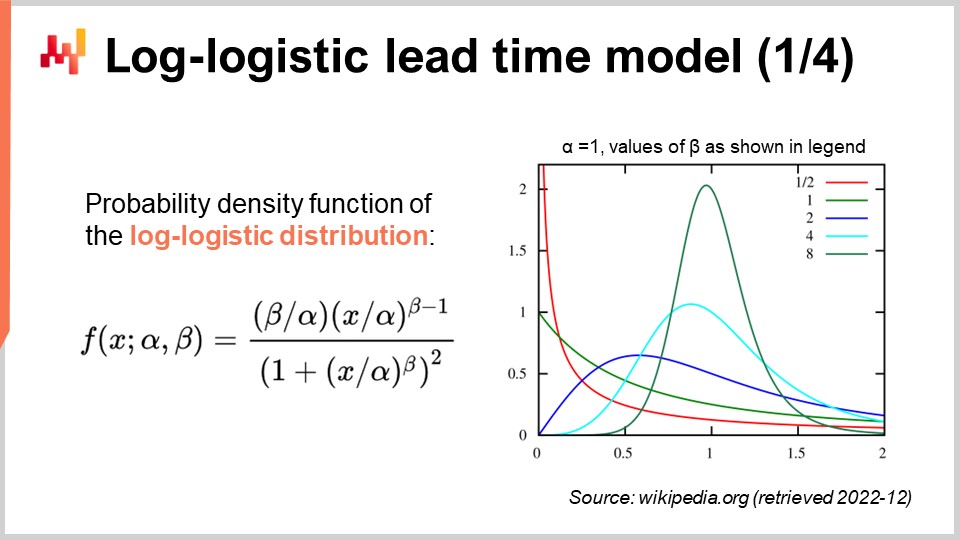
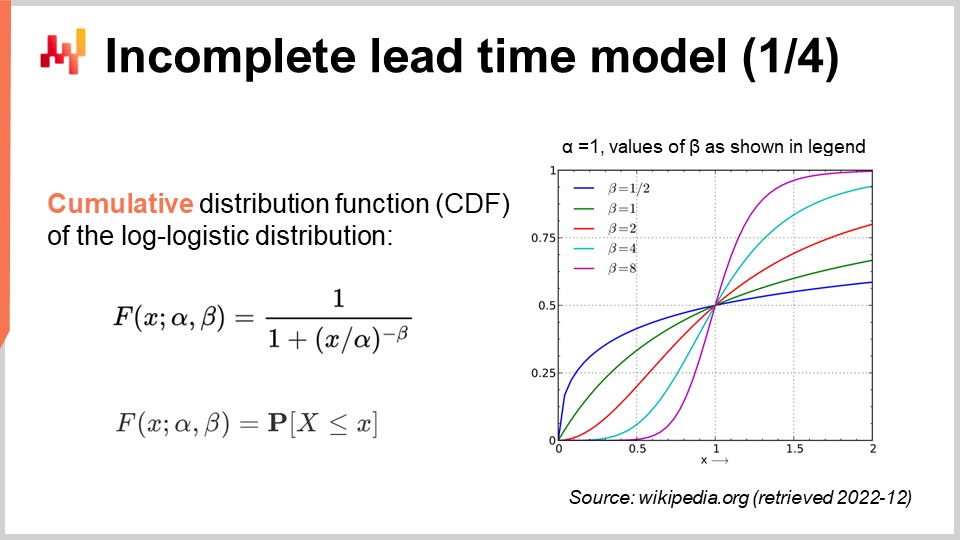
À l’écran, nous avons la fonction de densité de probabilité de la distribution log-logistique. Il s’agit d’une distribution paramétrique qui dépend de deux paramètres, alpha et beta. Le paramètre alpha est la médiane de la distribution, et le paramètre beta détermine la forme de la distribution. À droite, une courte série de formes peut être obtenue grâce à différentes valeurs de beta. Bien que cette formule de densité puisse sembler intimidante, elle relève littéralement du contenu d’un manuel scolaire, tout comme la formule permettant de calculer le volume d’une sphère. Vous pouvez essayer de déchiffrer et de mémoriser cette formule, mais ce n’est même pas nécessaire ; il vous suffit de savoir qu’une formule analytique existe. Une fois que vous savez que la formule existe, la retrouver en ligne prend moins d’une minute.

Notre objectif est de tirer parti de la distribution log-logistique pour élaborer un modèle probabiliste de lead time. Pour ce faire, nous allons minimiser la log-vraisemblance. En effet, lors de la conférence précédente de ce cinquième chapitre, nous avons vu qu’il existe plusieurs métriques appropriées pour la perspective probabiliste. Il y a peu, nous avons revisité le CRPS (Continuous Ranked Probability Score). Ici, nous revisitons la log-vraisemblance, qui adopte une perspective bayésienne.
En résumé, donnée deux paramètres, la distribution log-logistique nous indique la probabilité d’observer chaque donnée telle qu’elle apparaît dans l’ensemble de données empirique. Nous souhaitons apprendre les paramètres qui maximisent cette vraisemblance. Le logarithme, d’où la log-vraisemblance plutôt que la vraisemblance simple, est introduit pour éviter les sous-flux numériques. Les sous-flux numériques surviennent lorsque nous traitons des nombres très petits, très proches de zéro ; ces nombres très petits ne s’accordent pas bien avec la représentation en virgule flottante telle qu’on la retrouve généralement dans le matériel informatique moderne.
Ainsi, pour calculer la log-vraisemblance de la distribution log-logistique, nous appliquons le logarithme à sa fonction de densité de probabilité. L’expression analytique est affichée à l’écran. Cette expression peut être implémentée, et c’est exactement ce qui est fait dans les trois lignes de code ci-dessous.
À la ligne un, la fonction “L4” est présentée. L4 signifie “log-vraisemblance du log-logistic” – oui, il y a beaucoup de L et beaucoup de logs. Cette fonction prend trois arguments : les deux paramètres alpha et beta, ainsi que l’observation x. Cette fonction renvoie le logarithme de la vraisemblance. La fonction L4 est décorée avec le mot-clé “autodiff” ; ce mot-clé indique que cette fonction est destinée à être différentiée automatiquement. Autrement dit, les gradients peuvent rétropropager depuis la valeur de retour de cette fonction jusqu’à ses arguments, les paramètres alpha et beta. Techniquement, le gradient rétro-propage également à travers l’observation x ; cependant, comme nous garderons les observations immuables durant le processus d’apprentissage, les gradients n’auront aucun effet sur les observations. À la ligne trois, nous obtenons la transcription littérale de la formule mathématique juste au-dessus du script.
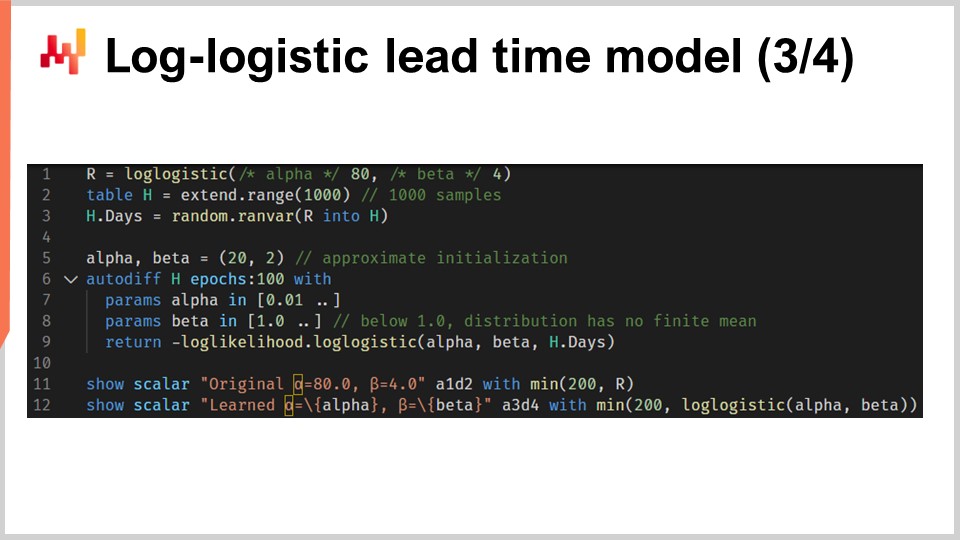
Regroupons maintenant le tout avec un script qui apprend les paramètres d’un modèle probabiliste de lead time basé sur la distribution log-logistique. Aux lignes un et trois, nous générons notre jeu de données d’entraînement factice. Dans des contextes réels, nous utiliserions des données historiques au lieu de générer des données factices. À la ligne un, nous créons un “ranvar” qui représente la distribution originale. Pour l’exercice, nous voulons réapprendre ces paramètres, alpha et beta. La fonction log-logistique fait partie de la bibliothèque standard d’Envision et elle renvoie un “ranvar”. À la ligne deux, nous créons la table “H”, qui contient 1 000 entrées. À la ligne trois, nous tirons 1 000 déviations aussitôt échantillonnées de la distribution originale “R”. Ce vecteur “H.days” représente le jeu de données d’entraînement.
À la ligne six, nous avons un bloc “autodiff” ; c’est là que l’apprentissage a lieu. Aux lignes sept et huit, nous déclarons deux paramètres, alpha et beta, et afin d’éviter des problèmes numériques tels que la division par zéro, des bornes sont appliquées à ces paramètres. Alpha doit rester supérieur à 0,01 et beta supérieur à 1,0. À la ligne neuf, nous renvoyons la perte, qui est l’inverse de la log-vraisemblance. En effet, par convention, les blocs “autodiff” minimisent la fonction de perte, et ainsi nous voulons maximiser la vraisemblance, d’où le signe moins. La fonction “log_likelihood.logistic” fait partie de la bibliothèque standard d’Envision, mais en réalité, ce n’est que la fonction “L4” que nous avons implémentée dans la diapositive précédente. Ainsi, il n’y a pas de magie en jeu ici ; c’est toute la différentiation automatique qui permet au gradient de rétropropager de la perte vers les paramètres alpha et beta.
Aux lignes 11 et 12, la distribution originale et la distribution apprise sont tracées. Les histogrammes sont bornés à 200 ; cette limite rend l’histogramme un peu plus lisible. Nous y reviendrons dans une minute. Au cas où vous vous poseriez des questions sur la performance de la partie “autodiff” de ce script, elle s’exécute en moins de 80 millisecondes sur un seul cœur CPU. La programmation différentiable n’est pas seulement polyvalente ; elle optimise également l’utilisation des ressources informatiques fournies par le matériel moderne.
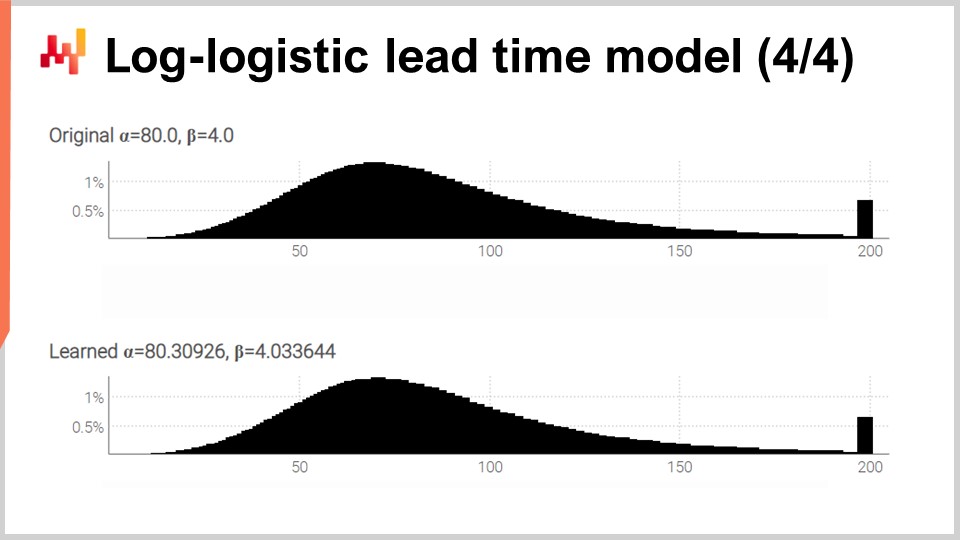
À l’écran, nous voyons les deux histogrammes produits par notre script que nous venons de passer en revue. En haut, la distribution originale avec ses deux paramètres initiaux, alpha et beta, fixés respectivement à 80 et 4. En bas, la distribution apprise avec deux paramètres appris grâce à la programmation différentiable. Ces deux pics à l’extrême droite sont associés aux queues que nous avons tronquées, car elles s’étendent assez loin. D’ailleurs, bien que ce soit rare, il arrive que certaines marchandises soient reçues plus d’un an après avoir été commandées. Ce n’est pas le cas dans tous les secteurs, certainement pas pour les produits laitiers, mais pour les pièces mécaniques ou l’électronique, cela arrive occasionnellement.
Bien que le processus d’apprentissage ne soit pas exact, nous obtenons des résultats dans un écart d’un pour cent par rapport aux valeurs initiales des paramètres. Cela démontre, au moins, que cette maximisation de la log-vraisemblance via la programmation différentiable fonctionne en pratique. La distribution log-logistique peut ou non être appropriée ; cela dépend de la forme de la distribution des lead times à laquelle vous êtes confronté. Toutefois, nous pouvons à peu près choisir n’importe quelle distribution paramétrique alternative. Il suffit d’une expression analytique de la fonction de densité de probabilité. Il existe une vaste gamme de telles distributions. Une fois que vous avez une formule de manuel, une implémentation directe via la programmation différentiable fait généralement le reste.
Les lead times ne sont pas observés uniquement une fois que la transaction est finalisée. Pendant que la transaction est encore en cours, vous savez déjà quelque chose ; vous disposez déjà d’une observation de lead time incomplète. Prenons l’exemple où, il y a 100 jours, vous avez passé une commande. Les marchandises n’ont pas encore été reçues ; cependant, vous savez déjà que le lead time est d’au moins 100 jours. Cette durée de 100 jours représente la limite inférieure d’un lead time qui n’a pas encore été entièrement observé. Ces lead times incomplets sont souvent assez importants. Comme je l’ai mentionné au début de cette conférence, les ensembles de données de lead times sont fréquemment clairsemés. Il n’est pas rare d’avoir un ensemble de données ne comprenant qu’une demi-douzaine d’observations. Dans ces situations, il est important de tirer le meilleur parti de chaque observation, y compris celles qui sont en cours.
Prenons l’exemple suivant : nous avons cinq commandes au total. Trois commandes ont déjà été livrées avec des valeurs de lead time très proches de 30 jours. Cependant, les deux dernières commandes sont en attente depuis respectivement 40 et 50 jours. Selon les trois premières observations, le lead time moyen devrait être d’environ 30 jours. Toutefois, les deux dernières commandes incomplètes contredisent cette hypothèse. Les deux commandes en souffrance à 40 et 50 jours suggèrent un lead time nettement plus long. Ainsi, nous ne devons pas rejeter les dernières commandes simplement parce qu’elles sont incomplètes. Nous devons tirer parti de cette information et mettre à jour notre conviction en faveur de lead times plus longs, peut-être 60 jours.
Revisitons notre modèle probabiliste de lead time, mais cette fois en tenant compte des observations incomplètes. Autrement dit, nous voulons traiter des observations qui sont parfois seulement une limite inférieure pour le lead time final. Pour ce faire, nous pouvons utiliser la fonction de répartition (CDF) de la distribution log-logistique. Cette formule est écrite à l’écran ; encore une fois, il s’agit de matériel de manuel scolaire. La CDF de la distribution log-logistique bénéficie d’une expression analytique simple. Par la suite, je ferai référence à cette technique comme la “conditional probability technique” pour gérer les données censurées.

En nous appuyant sur cette expression analytique de la CDF, nous pouvons revisiter la log-vraisemblance de la distribution log-logistique. Le script affiché présente une implémentation révisée de notre précédente implémentation L4. À la ligne un, nous avons pratiquement la même déclaration de fonction. Cette fonction prend un quatrième argument supplémentaire, une valeur booléenne nommée “is_incomplete” qui indique, comme son nom l’indique, si l’observation est incomplète ou non. Aux lignes deux et trois, si l’observation est complète, nous revenons à la situation précédente avec la distribution log-logistique classique. Ainsi, nous appelons la fonction de log-vraisemblance qui fait partie de la bibliothèque standard. J’aurais pu répéter le code de l’implémentation L4 précédente, mais cette version est plus concise. Aux lignes quatre et cinq, nous exprimons la log-vraisemblance d’observer finalement un lead time supérieur à l’observation incomplète actuelle, “X”. Ceci est réalisé via la CDF et, plus précisément, le logarithme de la CDF.
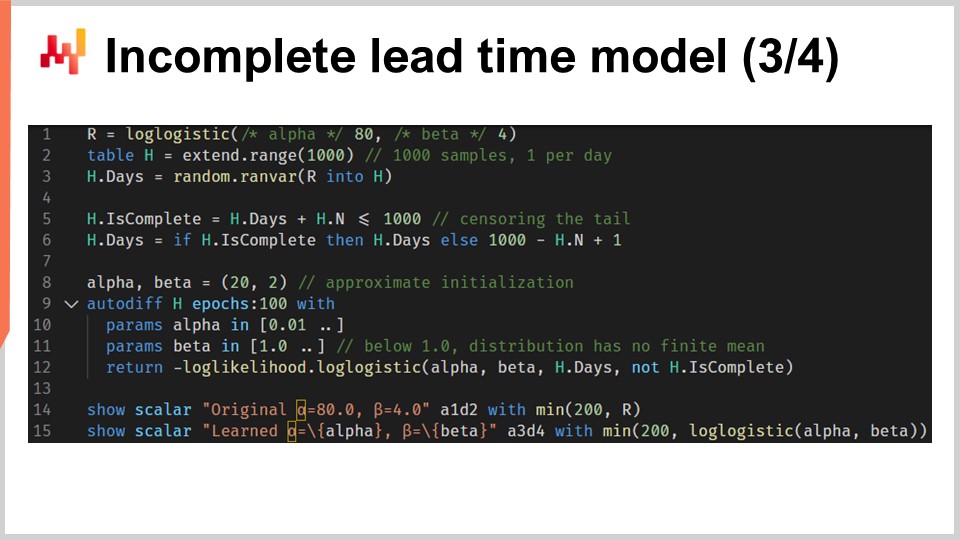
Nous pouvons maintenant répéter notre configuration avec un script qui apprend les paramètres de la distribution log-logistique, mais cette fois en présence de lead times incomplets. Le script affiché est presque identique au précédent. Aux lignes un à trois, nous générons les données ; ces lignes n’ont pas changé. Notons que H.N est un vecteur auto-généré qui est implicitement créé à la ligne deux. Ce vecteur numérote les lignes générées, à partir de un. La version précédente de ce script n’utilisait pas ce vecteur auto-généré, mais désormais, le vecteur H.N apparaît à la fin de la ligne six.
Les lignes cinq et six sont en effet les plus importantes. Ici, nous censurons les lead times. C’est comme si nous faisions une observation de lead time par jour et tronquions les observations trop récentes pour être informées. Cela signifie, par exemple, qu’un lead time de 20 jours initié il y a sept jours apparaît comme un lead time incomplet de sept jours. À la fin de la ligne six, nous avons généré une liste de lead times où certaines des observations récentes (celles qui se termineraient après la date actuelle) sont incomplètes. Le reste du script est inchangé, sauf à la ligne 12, où le vecteur H.is_complete est passé comme quatrième argument à la fonction de log-vraisemblance. Ainsi, nous appelons, à la ligne 12, la fonction de programmation différentiable que nous venons d’introduire il y a une minute.
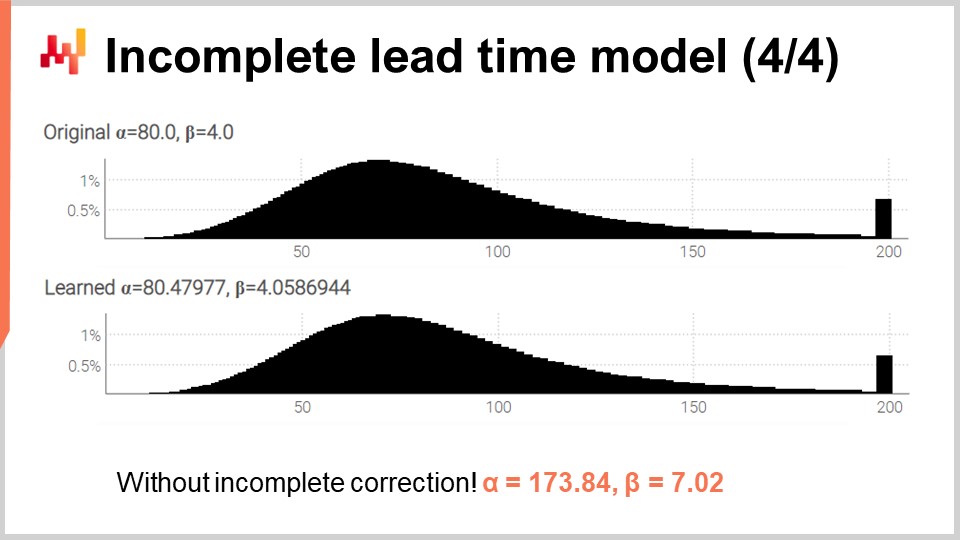
Enfin, à l’écran, les deux histogrammes sont produits par ce script révisé. Les paramètres sont toujours appris avec une grande précision, alors que nous sommes désormais en présence de nombreux lead times incomplets. Pour valider que traiter les temps incomplets n’était pas une complication inutile, j’ai réexécuté le script, mais cette fois avec une variation modifiée utilisant la surcharge à trois arguments de la fonction de log-vraisemblance (celle que nous avons utilisée initialement en supposant que toutes les observations étaient complètes). Pour alpha et beta, nous obtenons les valeurs affichées en bas de l’écran. Comme prévu, ces valeurs ne correspondent pas du tout aux valeurs initiales de alpha et beta.
Dans cette série de conférences, ce n’est pas la première fois qu’une technique est introduite pour traiter des données censurées. Dans la deuxième conférence de ce chapitre, la technique de masquage de la perte a été introduite pour gérer les ruptures de stock. En effet, nous souhaitons généralement prédire la demande future, et non les ventes futures. Les ruptures de stock introduisent un biais à la baisse, car nous ne pouvons pas observer toutes les ventes qui auraient eu lieu si la rupture de stock ne s’était pas produite. La technique de probabilité conditionnelle peut être utilisée pour traiter la demande censurée, comme c’est le cas pour les ruptures de stock. La technique de probabilité conditionnelle est un peu plus complexe que le masquage de perte, donc elle ne devrait probablement pas être utilisée si le masquage de perte est suffisant.
Dans le cas des lead times, la rareté des données est la motivation principale. Nous pouvons disposer de si peu de données qu’il peut être crucial de tirer le meilleur parti de chaque observation, même des observations incomplètes. En effet, la technique de probabilité conditionnelle est plus puissante que le masquage de perte dans la mesure où elle exploite les observations incomplètes au lieu de simplement les écarter. Par exemple, s’il y a une unité en stock et que cette unité est vendue, puis, suggérant une rupture de stock, la technique de probabilité conditionnelle utilise quand même l’information que la demande était supérieure ou égale à une.
Ici, nous obtenons un avantage surprenant de la modélisation probabiliste : elle nous offre une manière élégante de traiter la censure, un effet qui survient dans de nombreuses situations de supply chain. Grâce à la probabilité conditionnelle, nous pouvons éliminer des catégories entières de biais systémiques.
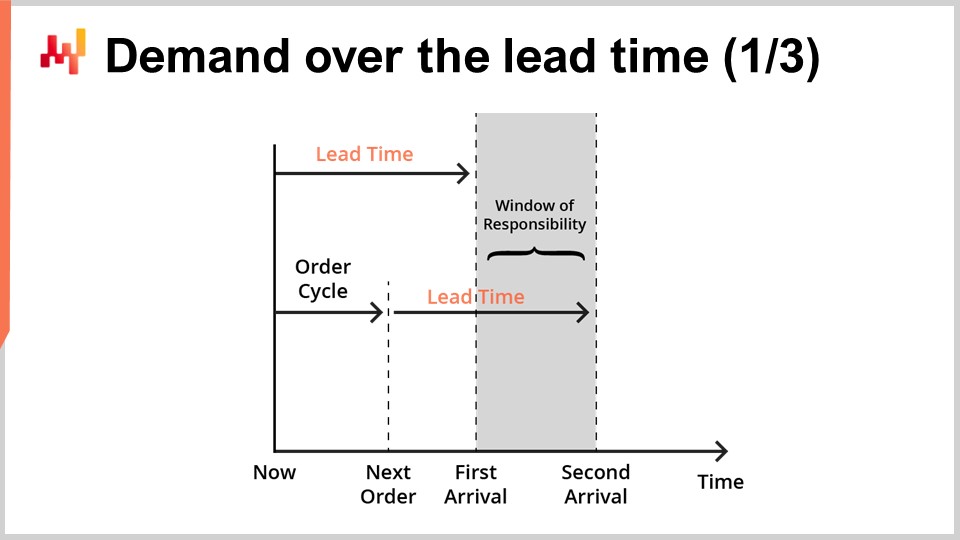
Les prévisions de délai de livraison sont généralement destinées à être combinées avec les prévisions de la demande. En effet, examinons maintenant une situation simple de réapprovisionnement de stocks, comme illustré à l’écran.
Nous desservons un seul produit, et les stocks peuvent être réapprovisionnés en repassant commande auprès d’un seul fournisseur. Nous recherchons une prévision qui appuierait notre décision de repasser commande ou non auprès du fournisseur. Nous pouvons repasser commande dès maintenant, et si nous le faisons, les marchandises arriveront au moment indiqué sous le nom de “first arrival.” Plus tard, nous aurons une autre opportunité de repasser commande. Cette opportunité ultérieure survient à un moment désigné par “next order,” et dans ce cas, les marchandises arriveront au moment indiqué sous le nom de “second arrival.” La période désignée par la “window of responsibility” est celle qui importe pour notre décision de repasser commande.
En effet, quoi que nous décidions de repasser commande, cela n’arrivera pas avant le premier délai de livraison. Ainsi, nous avons déjà perdu le contrôle pour satisfaire la demande pour tout ce qui se passe avant la première arrivée. Ensuite, comme nous aurons une opportunité ultérieure de repasser commande, satisfaire la demande après la deuxième arrivée n’est plus de notre ressort ; cela relève de la responsabilité de la prochaine commande. Par conséquent, repasser commande en ayant l’intention de satisfaire une demande au-delà de la deuxième arrivée doit être reporté jusqu’à la prochaine opportunité.
Pour soutenir la décision de repasser commande, deux facteurs doivent être prévus. Premièrement, nous devons prévoir le stock disponible attendu au moment de la première arrivée. En effet, si, à l’heure de la première arrivée, il reste encore beaucoup de stocks, il n’y a alors aucune raison de repasser commande dès maintenant. Deuxièmement, nous devons prévoir la demande attendue pour la durée de la window of responsibility. Dans une configuration réelle, il faudrait également prévoir la demande au-delà de la window of responsibility afin d’évaluer le carrying cost des marchandises que nous commandons actuellement, puisqu’il pourrait y avoir des excédents qui se prolongent sur des périodes ultérieures. Toutefois, par souci de concision et de timing, nous allons nous concentrer aujourd’hui sur le stock attendu et la demande attendue dans le cadre de la window of responsibility.
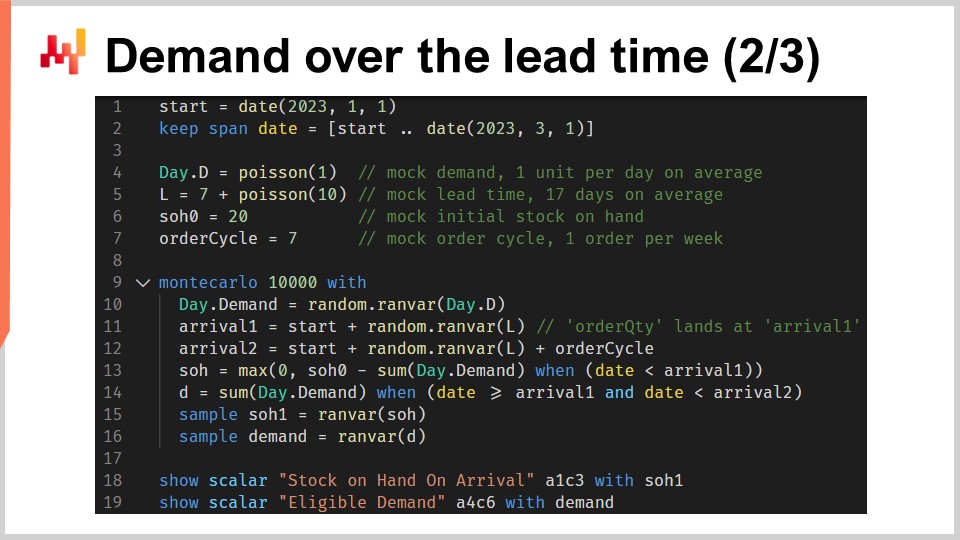
Ce script implémente les facteurs de la window of responsibility ou prévisions dont nous venons de discuter. Il prend en entrée une prévision probabiliste de délai de livraison et une prévision probabiliste de la demande. Il renvoie deux distributions de probabilités, à savoir le stock disponible à l’arrivée et la demande éligible telle que définie par la window of responsibility.
Aux lignes un et deux, nous configurons les chronologies, qui commencent le 1er janvier et se terminent le 1er mars. Dans une configuration de prévision, cette chronologie ne serait pas codée en dur. À la ligne quatre, un modèle probabiliste simpliste de la demande est introduit : une distribution de Poisson répétée jour après jour sur toute la durée de cette chronologie. La demande sera en moyenne d’une unité par jour. J’utilise ici un modèle simpliste pour la demande par souci de clarté. Dans une configuration réelle, nous utiliserions, par exemple, un ESSM (Ensemble State Space Model). Les modèles d’état sont probabilistes, et ils ont été présentés dès la première conférence de ce chapitre.
À la ligne cinq, un autre modèle probabiliste simpliste est introduit. Ce second modèle est destiné aux délais de livraison. Il s’agit d’une distribution de Poisson décalée de sept jours vers la droite. Le décalage est effectué par convolution. À la ligne six, nous définissons le stock initial disponible. À la ligne sept, nous définissons le cycle de commande. Cette valeur, exprimée en jours, caractérise le moment où aura lieu la prochaine commande.
De la ligne 9 à 16, nous avons un bloc Monte Carlo qui représente le cœur de la logique du script. Plus tôt dans cette conférence, nous avions déjà introduit un autre bloc Monte Carlo pour soutenir notre logique de validation croisée. Ici, nous utilisons à nouveau cette construction, mais pour un objectif différent. Nous souhaitons calculer deux variables aléatoires reflétant, respectivement, le stock disponible à l’arrivée et la demande éligible. Cependant, l’algèbre des variables aléatoires n’est pas suffisamment expressive pour effectuer ce calcul. Ainsi, nous utilisons à la place un bloc Monte Carlo.
Dans la troisième conférence de ce chapitre, j’ai souligné qu’il existait une dualité entre la prévision probabiliste et les simulations. Le bloc Monte Carlo illustre parfaitement cette dualité. Nous partons d’une prévision probabiliste, la transformons en simulation, puis convertissons les résultats de la simulation en une autre prévision probabiliste.
Examinons les détails. À la ligne 10, nous générons une trajectoire pour la demande. À la ligne 11, nous générons la date d’arrivée pour la première commande, en supposant que nous commandons aujourd’hui. À la ligne 12, nous générons la date d’arrivée pour la deuxième commande, en supposant que nous repassons commande dans un cycle de commande. À la ligne 13, nous calculons ce qui reste en stocks à la date de la première arrivée. Il s’agit du stock initial moins la demande observée durant le premier délai de livraison. Le “max zéro” indique que le stock ne peut pas devenir négatif. En d’autres termes, nous supposons qu’il n’y a aucun arriéré. Ce postulat de non-arriéré pourrait être modifié. Le cas de l’arriéré est laissé comme exercice pour le public. À titre d’indice, la programmation différentiable peut être utilisée pour évaluer le pourcentage de la demande non satisfaite qui se convertit avec succès en arriérés, en fonction du nombre de jours avant la disponibilité renouvelée des stocks.
Pour revenir au script, à la ligne 14, nous calculons la demande éligible, c’est-à-dire la demande qui se produit pendant la window of responsibility. Aux lignes 15 et 16, nous recueillons deux variables aléatoires d’intérêt via le mot-clé “sample”. Contrairement au premier script Envision de cette conférence, qui traitait de la validation croisée, nous cherchons ici à recueillir des distributions de probabilités issues de ce bloc Monte Carlo, et non simplement des moyennes. Sur les lignes 15 et 16, la variable aléatoire figurant à droite de l’affectation est un agrégateur. À la ligne 15, nous obtenons une variable aléatoire pour le stock disponible à l’arrivée. À la ligne 16, nous obtenons une autre variable aléatoire pour la demande se produisant pendant la window of responsibility.
Aux lignes 18 et 19, ces deux variables aléatoires sont affichées. Prenons maintenant un instant pour faire une pause et reconsidérer l’ensemble du script. Les lignes un à sept sont uniquement dédiées à la configuration des données factices. Les lignes 18 et 19 se contentent d’afficher les résultats. La seule logique effective se situe sur les huit lignes comprises entre les lignes 9 et 16. En fait, toute la logique effective se trouve, en quelque sorte, aux lignes 13 et 14.
En seulement quelques lignes de code, moins de 10 quoi qu’on en dise, nous combinons une prévision probabiliste de délai de livraison avec une prévision probabiliste de la demande afin de constituer une sorte de prévision probabiliste hybride d’une réelle importance pour la supply chain. Notons qu’il n’y a rien ici qui dépende réellement des spécificités de la prévision de délai de livraison ou de celle de la demande. Des modèles simples ont été utilisés, mais des modèles sophistiqués auraient très bien pu être employés à la place. Cela n’aurait rien changé. L’unique exigence est de disposer de deux modèles probabilistes afin de pouvoir générer ces trajectoires.
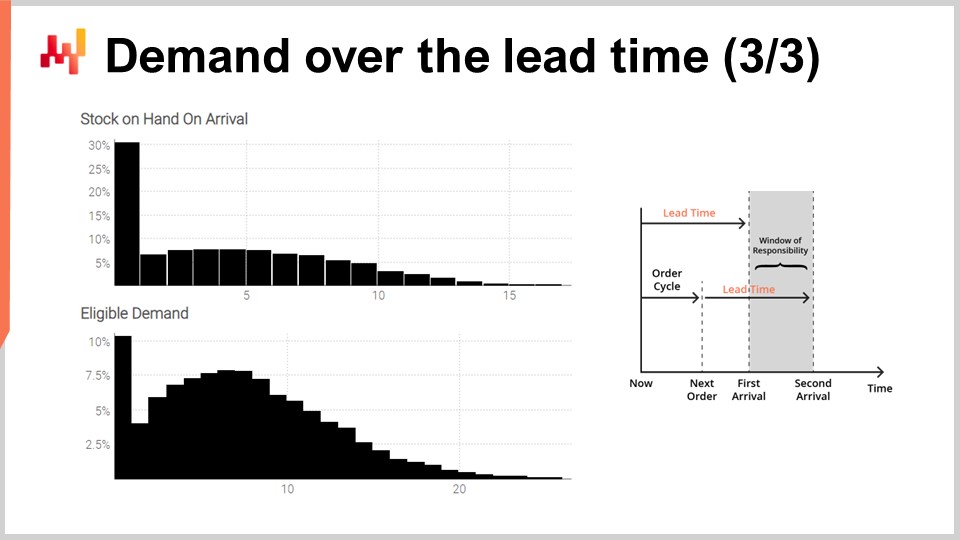
Enfin, à l’écran, les histogrammes produits par le script. L’histogramme supérieur représente le stock disponible à l’arrivée. Il y a environ 30 % de chances de se retrouver avec un stock initial nul. Autrement dit, il y a 30 % de chances qu’une rupture de stock soit survenue le jour précédent la première arrivée. La valeur moyenne du stock pourrait être d’environ cinq unités. Cependant, si nous devions juger cette situation uniquement sur la moyenne, nous interpréterions gravement la situation. Une prévision probabiliste est essentielle pour refléter correctement la situation initiale des stocks.
L’histogramme inférieur représente la demande associée à la window of responsibility. Nous avons environ 10 % de chances d’observer une demande nulle. Ce résultat peut également sembler surprenant. En effet, nous avons débuté cet exercice avec une demande stationnaire selon une loi de Poisson, d’une unité par jour en moyenne. Nous disposons de sept jours entre les commandes. Si ce n’était pas à cause du délai de livraison variable, il y aurait eu moins de 0,1 % de chances d’obtenir une demande nulle sur sept jours. Cependant, le script démontre que cette occurrence est bien plus fréquente. La raison en est qu’une window of responsibility réduite peut survenir si le premier délai de livraison est plus long que d’habitude et si le deuxième délai de livraison est plus court que d’habitude.
Observer une demande nulle pendant la window of responsibility signifie que le stock disponible risque de devenir assez élevé à un moment donné. Selon la situation, cela peut ou non être critique, par exemple si une capacité de stockage limitée existe ou si les stocks sont périssables. Encore une fois, la demande moyenne, probablement d’environ huit, ne fournit pas une vision fiable de la réalité de la demande. Rappelons que nous avons obtenu cette distribution fortement asymétrique à partir d’une demande stationnaire initiale, d’une unité par jour en moyenne. C’est l’effet du délai de livraison variable en action.
Cette configuration simple démontre l’importance des délais de livraison dans les situations de réapprovisionnement de stocks. D’un point de vue supply chain, isoler les prévisions de délai de livraison des prévisions de la demande constitue, au mieux, une abstraction pratique. La demande quotidienne n’est pas ce qui nous intéresse réellement. Ce qui importe véritablement, c’est la composition de la demande avec le délai de livraison. Si d’autres facteurs stochastiques étaient présents, comme des arriérés ou des retours, ces facteurs feraient également partie du modèle.

Le présent chapitre de cette série de conférences est intitulé “Predictive Modeling” au lieu de “Demand Forecasting”, comme ce serait typiquement le cas dans les manuels de supply chain grand public. La raison de ce titre de chapitre devrait être devenue progressivement évidente au fil de la conférence. En effet, d’un point de vue supply chain, nous souhaitons prévoir l’évolution du système de supply chain. La demande est certes un facteur important, mais ce n’est pas le seul. D’autres facteurs variables, comme le délai de livraison, doivent être prévus. Plus important encore, tous ces facteurs doivent, en fin de compte, être prévus ensemble.
En effet, nous devons rassembler ces composantes prédictives pour soutenir un processus de decision-making. Ainsi, l’essentiel n’est pas de chercher un modèle de prévision de la demande ultime. Cette tâche s’avère en grande partie vaine, car la précision supplémentaire sera obtenue de manière contraire aux intérêts de l’entreprise. Plus le modèle est sophistiqué, plus il devient opaque, engendre de bugs et nécessite de ressources informatiques. En règle générale, plus le modèle est sophistiqué, plus il devient difficile de le composer opérationnellement avec un autre modèle. Ce qui importe, c’est d’assembler une collection de techniques prédictives qui peuvent être composées à volonté. Voilà ce qu’englobe la modularité d’un point de vue de la modélisation prédictive. Dans cette conférence, une demi-douzaine de techniques ont été présentées. Ces techniques sont utiles car elles abordent des aspects critiques du monde réel, comme les observations incomplètes. Elles sont également simples ; aucun des exemples de code présentés aujourd’hui n’a dépassé 10 lignes de logique effective. Et surtout, ces techniques sont modulaires, comme des briques Lego. Elles fonctionnent bien ensemble et peuvent être recomposées presque à l’infini.
L’objectif ultime de la modélisation prédictive pour la supply chain, tel qu’il doit être compris, est l’identification de telles techniques. Chaque technique devrait, en soi, offrir l’opportunité de revisiter tout modèle prédictif préexistant afin de le simplifier ou de l’améliorer.

En conclusion, bien que le délai de livraison soit largement ignoré par la communauté académique, il peut et doit être prédit. En passant en revue une courte série de distributions réelles de délais de livraison, nous avons identifié deux défis : premièrement, les délais varient ; deuxièmement, ils sont rares. Ainsi, nous avons introduit des techniques de modélisation appropriées pour traiter des observations de délais de livraison à la fois rares et erratiques.
Ces modèles de délai de livraison sont probabilistes et constituent, dans une large mesure, la continuité des modèles progressivement introduits au fil de ce chapitre. Nous avons également constaté que la perspective probabiliste offre une solution élégante au problème des observations incomplètes, un aspect presque omniprésent dans la supply chain. Ce problème survient chaque fois qu’il y a des ruptures de stocks ou des commandes en attente. Enfin, nous avons vu comment composer une prévision probabiliste de délai de livraison avec une prévision probabiliste de la demande afin de concevoir le modèle prédictif nécessaire pour soutenir un processus de décision ultérieur.

La prochaine conférence aura lieu le 8 mars. Ce sera un mercredi à la même heure, 15h, heure de Paris. La conférence d’aujourd’hui était technique, mais la suivante sera en grande partie non technique, et j’y aborderai le cas du supply chain scientist. En effet, les manuels de supply chain grand public traitent la supply chain comme si les modèles de prévision et d’optimisation apparaissaient et fonctionnaient par magie, en ignorant complètement leur composante “wetware” — c’est-à-dire, les personnes en charge. Ainsi, nous examinerons de plus près les rôles et responsabilités du supply chain scientist, une personne censée piloter l’initiative de la Supply Chain Quantitative.
Maintenant, je vais passer aux questions.
Question: Et si quelqu’un veut conserver ses stocks pour favoriser l’innovation ou pour des raisons autres que le juste-à-temps ou d’autres concepts ?
C’est en effet une question très importante. Le concept est généralement abordé à travers la modélisation économique de la supply chain, que nous appelons techniquement les “economic drivers” dans cette série de conférences. Ce que vous demandez, c’est s’il vaut mieux ne pas servir un client aujourd’hui parce qu’à un moment ultérieur, il y aura l’opportunité de servir la même unité à une autre personne qui revêt une plus grande importance pour une raison ou une autre. En substance, ce que vous affirmez, c’est qu’il y a davantage de valeur à être capturée en servant ultérieurement un autre client, peut-être un client VIP, plutôt qu’en servant un client aujourd’hui.
Cela pourrait être le cas, et cela arrive effectivement. Par exemple, dans l’industrie aéronautique, supposons que vous soyez un fournisseur MRO (Maintenance, Repair, and Overhaul). Vous avez vos clients VIP habituels — les compagnies aériennes que vous servez régulièrement avec des contrats à long terme, et ils sont très importants. Quand cela se produit, vous souhaitez vous assurer de pouvoir toujours servir ces clients. Mais que se passe-t-il si une autre compagnie aérienne vous appelle et demande une seule unité ? Dans ce cas, ce qui se passera, c’est que vous pourrez servir cette personne, mais vous n’avez pas de contrat à long terme avec elle. Donc, ce que vous ferez sera d’ajuster votre prix pour qu’il soit très élevé, garantissant ainsi que vous obteniez suffisamment de valeur pour compenser la potentielle rupture de stock que vous pourriez subir ultérieurement. En résumé, pour cette première question, je crois qu’il ne s’agit pas vraiment de prévision mais plutôt d’une modélisation adéquate des leviers économiques. Si vous voulez préserver des stocks, vous devez générer un modèle — un modèle d’optimisation — dans lequel la réponse rationnelle n’est pas de servir le client qui demande une seule unité pendant que vous avez encore des stocks en réserve.
Soit dit en passant, une autre situation typique se présente lorsque vous vendez des kits. Un kit est un assemblage de nombreuses pièces vendu ensemble, et il vous reste une seule pièce qui ne représente qu’une petite fraction de la valeur totale du kit. Le problème est que si vous vendez cette dernière unité, vous ne pourrez plus assembler votre kit et le vendre à son plein prix. Ainsi, vous pourriez vous retrouver dans une situation où vous préférez conserver l’unité en stock simplement afin de pouvoir vendre le kit ultérieurement, potentiellement avec une certaine incertitude. Mais encore une fois, tout se résume aux leviers économiques, et c’est ainsi que j’aborderais cette situation.
Question : Au cours des dernières années, la plupart des retards de supply chain se sont produits en raison de la guerre ou d’une pandémie, ce qui est très difficile à prévoir car nous n’avions pas connu de telles situations auparavant. Quel est votre avis à ce sujet ?
Selon moi, les délais ont toujours été variables. Je fais partie du monde de la supply chain depuis 2008, et mes parents travaillaient dans la supply chain même 30 ans avant moi. Autant que nous nous en souvenions, les délais ont toujours été erratiques et fluctuants. Il se passe toujours quelque chose, qu’il s’agisse d’une manifestation, d’une guerre ou d’un changement de tarifs. Certes, ces dernières années ont été particulièrement erratiques, mais les délais variaient déjà énormément.
Je suis d’accord pour dire que personne ne peut prétendre être capable de prévoir la prochaine guerre ou la prochaine pandémie. Si l’on pouvait prédire ces événements mathématiquement, les gens ne se lanceraient pas dans des guerres ni n’investiraient dans la supply chain ; ils se contenteraient de jouer en bourse et deviendraient riches en anticipant les mouvements du marché.
Le fond du problème est que ce que vous pouvez faire, c’est planifier l’inattendu. Si vous n’êtes pas confiant quant à l’avenir, vous pouvez en fait augmenter les variations dans vos prévisions. C’est le contraire de chercher à rendre votre prévision plus précise — vous conservez vos attentes moyennes, mais vous amplifiez simplement la queue afin que les décisions que vous prenez sur la base de ces prévisions probabilistes soient plus résilientes face aux variations. Vous avez conçu vos variations attendues pour qu’elles soient plus importantes que ce que vous observez actuellement. En résumé, l’idée que certaines choses soient faciles ou difficiles à prévoir vient d’une perspective de prévision ponctuelle, où l’on voudrait jouer comme s’il était possible d’anticiper précisément l’avenir. Ce n’est pas le cas — il n’existe pas d’anticipation précise de l’avenir. La seule chose que vous puissiez faire est de travailler avec des distributions de probabilité à grande étendue qui manifestent et quantifient votre ignorance du futur.
Au lieu de peaufiner des décisions qui dépendent de l’exécution minutieuse d’un plan exact, vous prenez en compte et planifiez un certain degré de variation, rendant ainsi vos décisions plus robustes face à ces variations. Cependant, cela ne s’applique qu’au type de variation qui n’impacte pas votre supply chain de manière trop brutale. Par exemple, vous pouvez gérer des délais fournisseurs plus longs, mais si votre warehouse a été bombardé, aucune prévision ne pourra vous sauver dans une telle situation.
Question : Pouvons-nous créer ces histogrammes et calculer le CRPS dans Microsoft Excel, par exemple, en utilisant des add-ins Excel comme itsastat ou ceux qui hébergent de nombreuses distributions ?
Oui, vous le pouvez. L’un d’entre nous chez Lokad a en fait réalisé une feuille de calcul Excel qui représente un modèle probabiliste pour une situation de réapprovisionnement de stocks. Le cœur du problème est qu’Excel ne dispose pas d’un type de donnée histogramme natif, donc tout ce que vous avez dans Excel, ce sont des nombres — une cellule, un nombre. Il serait élégant et simple d’avoir une valeur qui soit un histogramme, où vous auriez un histogramme complet contenu dans une seule cellule. Cependant, autant que je sache, cela n’est pas possible dans Excel. Néanmoins, si vous êtes prêt à consacrer environ 100 lignes ou quelque chose du genre pour représenter l’histogramme, même si cela ne sera pas aussi compact et pratique, vous pouvez implémenter une distribution dans Excel et faire de la modélisation probabiliste. Nous posterons le lien vers l’exemple dans la section des commentaires.
Gardez à l’esprit que c’est une entreprise relativement pénible, car Excel n’est pas idéal pour cette tâche. Excel est un langage de programmation, et vous pouvez y faire n’importe quoi, donc vous n’avez même pas besoin d’un add-in pour y parvenir. Cependant, cela sera un peu verbeux, alors ne vous attendez pas à quelque chose de super soigné.
Question : Le lead time peut être décomposé en composantes telles que le temps de commande, le temps de production, le temps de transport, etc. Si l’on souhaite un contrôle plus granulaire sur les délais, comment cette approche évoluerait-elle ?
Tout d’abord, nous devons considérer ce que signifie avoir plus de contrôle sur le délai. Voulez-vous réduire le délai moyen ou diminuer la variabilité du délai ? Fait intéressant, j’ai vu de nombreuses entreprises réussir à réduire le délai moyen, mais au prix d’une variation supplémentaire des délais. En moyenne, le délai est plus court, mais de temps à autre, il est bien plus long.
Dans cette conférence, nous nous lançons dans un exercice de modélisation. En soi, il n’y a pas d’action ; il s’agit simplement d’observer, d’analyser et de prédire. Cependant, si nous pouvons décomposer le délai et analyser la distribution sous-jacente, nous pouvons utiliser la modélisation probabiliste pour évaluer quelles composantes varient le plus et lesquelles ont le négatif le plus significatif sur notre supply chain. Nous pouvons envisager des scénarios du type « et si ? » avec ces informations. Par exemple, prenez une partie de votre délai et demandez-vous : « Et si la queue de ce délai était un peu plus courte, ou si la moyenne était un peu plus courte ? » Vous pouvez alors recomposer l’ensemble, relancer votre modèle prédictif pour l’intégralité de votre supply chain, et commencer à en évaluer l’impact.
Cette approche vous permet de raisonner par parties sur certains phénomènes, y compris les comportements erratiques. Il ne s’agit pas tant d’un changement d’approche que de la continuation de ce que nous avons déjà fait, menant au Chapitre 6, qui traite de l’optimisation des décisions concrètes basées sur ces modèles probabilistes.
Question : Je pense que cela offre l’opportunité de recalculer nos délais dans SAP afin de fournir un échéancier plus réaliste et d’aider à minimiser notre système de pull-in et pull-out. Est-ce possible ?
Avertissement : SAP est un concurrent de Lokad dans le domaine de l’optimisation de la supply chain. Ma réponse initiale est non, SAP ne peut pas faire cela. La réalité est que SAP propose quatre solutions distinctes qui traitent de l’optimisation de la supply chain, et cela dépend de la pile dont on parle. Cependant, toutes ces piles ont en commun une vision centrée sur les prévisions ponctuelles. Tout chez SAP a été conçu sur la prémisse que les prévisions seraient précises.
Oui, SAP dispose de quelques paramètres à ajuster, comme la distribution normale que j’ai mentionnée au début de cette conférence. Cependant, les distributions des délais que nous avons observées n’étaient pas distribuées normalement. À ma connaissance, les configurations SAP grand public pour l’optimisation de la supply chain adoptent une distribution normale pour les délais. Le problème est qu’au fond, le logiciel repose sur une hypothèse mathématique largement erronée. Vous ne pouvez pas compenser une hypothèse largement incorrecte qui se trouve au cœur de votre architecture logicielle en ajustant un paramètre. Peut-être pouvez-vous faire un ingénierie inverse folle et trouver un paramètre qui finirait par générer la bonne décision. Théoriquement, c’est possible, mais en pratique, cela pose tellement de problèmes que la question se pose : pourquoi voudriez-vous vraiment faire cela ?
Pour adopter une perspective probabiliste, vous devez vous engager pleinement, c’est-à-dire que vos prévisions sont probabilistes et que vos modèles d’optimisation utilisent également des modèles probabilistes. Le problème ici est que, même si nous pouvions ajuster la modélisation probabiliste pour obtenir des délais légèrement meilleurs, le reste de la pile SAP retomberait sur des prévisions ponctuelles. Quoi qu’il arrive, nous réduirons ces distributions à des points. L’idée que vous pourriez approximativement remplacer cela par une moyenne est troublante et tout simplement erronée. Ainsi, techniquement, vous pourriez ajuster les délais, mais vous allez rencontrer tellement de problèmes par la suite qu’il pourrait ne pas valoir l’effort.
Question : Il arrive que vous commandiez les mêmes pièces auprès de différents fournisseurs. Ceci est une information importante à prendre en compte dans la prévision des délais. Faites-vous des prévisions de délais par article ou y a-t-il des situations où vous profitez de regrouper des articles en familles ?
C’est une question remarquablement intéressante. Nous avons deux fournisseurs pour le même article. La question sera de savoir quelle est la similitude entre les articles et les fournisseurs. Tout d’abord, il faut examiner la situation. Si l’un des fournisseurs se trouve juste à côté et l’autre à l’autre bout du monde, il est vraiment nécessaire de les considérer séparément. Mais supposons la situation intéressante où les deux fournisseurs sont assez similaires et qu’il s’agit du même article. Faut-il regrouper ces observations ou non ?
Ce qui est intéressant, c’est qu’avec la programmation différentiable, vous pouvez composer un modèle qui attribue un certain poids au fournisseur et un certain poids à l’article, et laisser la magie de l’apprentissage opérer. Il s’agira de déterminer s’il faut accorder plus de poids à la composante liée à l’article dans le délai ou à celle du fournisseur. Il se peut que deux fournisseurs offrant à peu près le même type de produits présentent un biais, l’un étant, en moyenne, un peu plus rapide que l’autre. Mais certains articles prennent indéniablement plus de temps, et ainsi, si vous ne sélectionnez que certains articles, il n’est pas très évident qu’un fournisseur soit plus rapide que l’autre, car cela dépend réellement des articles considérés. Vous disposez probablement de très peu de données si vous désagrégez tout pour chaque fournisseur et chaque article. Ainsi, l’aspect intéressant, et ce que je recommanderais ici, est de concevoir via la programmation différentiable. Nous pourrions même essayer de revisiter cette situation dans une conférence ultérieure, une situation où vous attribuez certains paramètres au niveau de l’article et d’autres au niveau du fournisseur. Ainsi, vous obtiendrez un nombre total de paramètres qui ne sera pas égal au nombre d’articles multiplié par le nombre de fournisseurs, mais plutôt le nombre d’articles plus le nombre de fournisseurs, ou peut-être plus le nombre de fournisseurs multiplié par des catégories, ou quelque chose de similaire. Vous n’explosez pas votre nombre de paramètres ; vous ajoutez simplement un paramètre, un élément qui a une affinité avec le fournisseur, et qui vous permet d’effectuer une sorte de mélange dynamique guidé par vos données historiques.
Question : Je pense que la quantité commandée et les produits commandés ensemble pourraient également influencer le délai au final. Pourriez-vous passer en revue la complexité d’inclure toutes les variables dans ce type de problème ?
Dans le dernier exemple, nous avions deux types de durée : le cycle de commande et le délai lui-même. Le cycle de commande est intéressant car il n’est incertain que dans la mesure où nous n’avons pas encore pris la décision. C’est fondamentalement quelque chose que vous pouvez décider pratiquement à tout moment, donc le cycle de commande est entièrement interne et résulte de votre propre initiative. Ce n’est pas le seul aspect de la supply chain à présenter cela ; les prix le sont de la même manière. Vous avez une demande, vous observez la demande, mais vous pouvez en réalité choisir le prix que vous souhaitez. Certains prix sont évidemment imprudents, mais c’est pareil — ils relèvent de votre propre choix.
Le cycle de commande relève de votre propre initiative. Maintenant, ce que vous dites, c’est qu’il existe une incertitude quant au moment précis du prochain délai de commande, car vous ne savez pas exactement quand vous passerez commande. En effet, vous avez tout à fait raison. Ce qui se passe, c’est que lorsque vous avez la capacité de mettre en œuvre cette modélisation probabiliste, soudainement, comme nous l’avons évoqué dans le sixième chapitre de cette série de conférences, vous ne souhaitez plus dire que le cycle de commande est de sept jours. Au contraire, vous souhaitez adopter une politique de réapprovisionnement qui maximise le retour sur investissement pour votre entreprise. Ainsi, ce que vous pouvez faire, c’est planifier l’avenir de façon à ce que, si vous commandez maintenant, vous puissiez prendre une décision immédiatement, puis appliquer votre politique jour après jour. À un moment donné dans le futur, vous effectuerez une nouvelle commande, et alors vous vous retrouverez dans une sorte de situation de « serpent qui se mord la queue » puisque la meilleure décision de commande pour aujourd’hui dépend de la décision relative à la prochaine commande, celle que vous n’avez pas encore prise. Ce type de problème est connu sous le nom de problème de politique, et c’est un problème de décision séquentielle. En substance, ce que vous souhaitez réellement, c’est élaborer une sorte de politique, un objet mathématique qui régit votre processus de prise de décision.
Le problème de l’optimisation des politiques est assez complexe, et j’ai l’intention de l’aborder dans le sixième chapitre. Mais en fin de compte, si nous revenons à votre question, nous avons deux composantes distinctes. D’une part, la composante qui varie indépendamment de ce que vous faites, c’est-à-dire le délai, qui correspond au délai fournisseur, et d’autre part, le temps de commande, qui est véritablement interne à votre processus et doit être traité comme une question d’optimisation.
Pour conclure ce propos, nous constatons une convergence entre l’optimisation et la modélisation prédictive. En fin de compte, les deux finissent par être presque la même chose, car il existe des interactions entre les décisions que vous prenez et ce qui se passe dans le futur.
C’est tout pour aujourd’hui. N’oubliez pas, le 8 mars, à la même heure, ce sera un mercredi, à 15h. Merci, et à la prochaine fois.


