Generalizzazione (Previsione)
La generalizzazione è la capacità di un algoritmo di generare un modello - sfruttando un dataset - che funzioni bene su dati precedentemente non visti. La generalizzazione è di importanza critica per la supply chain, poiché la maggior parte delle decisioni riflette un’anticipazione del futuro. Nel contesto delle previsioni, i dati non sono osservabili perché il modello predice eventi futuri, che non possono essere osservati. Sebbene siano stati compiuti progressi sostanziali, sia teorici che pratici, sul fronte della generalizzazione dagli anni ‘90, la vera generalizzazione rimane sfuggente. La risoluzione completa del problema della generalizzazione potrebbe non essere molto diversa da quella del problema dell’intelligenza artificiale generale. Inoltre, la supply chain aggiunge una serie di complicazioni spinose alle sfide principali della generalizzazione.
Panoramica di un paradosso
Creare un modello che funzioni perfettamente sui dati a disposizione è semplice: basta memorizzare interamente il dataset e poi utilizzare lo stesso dataset per rispondere a qualsiasi richiesta in merito. Poiché i computer sono abili nel registrare grandi dataset, progettare un tale modello è facile. Tuttavia, di solito risulta inutile1, poiché l’essenza del possedere un modello risiede nel suo potere predittivo oltre ciò che è già stato osservato.
Si presenta un paradosso apparentemente ineluttabile: un buon modello è quello che funziona bene su dati attualmente indisponibili ma, per definizione, se i dati sono indisponibili, l’osservatore non può effettuare la valutazione. Il termine “generalizzazione”, pertanto, si riferisce all’elusiva capacità di certi modelli di mantenere la loro rilevanza e qualità al di là delle osservazioni disponibili al momento della costruzione del modello.
Pur potendo considerarsi la memorizzazione delle osservazioni come una strategia di modellazione inadeguata, qualsiasi strategia alternativa per creare un modello è potenzialmente soggetta allo stesso problema. Non importa quanto bene il modello sembri funzionare sui dati attualmente disponibili, è sempre concepibile che si tratti solo di una questione di caso, o peggio, di un difetto della strategia di modellazione. Ciò che a prima vista potrebbe apparire come un paradosso statistico marginale, in realtà, è una questione di ampia portata.
A titolo di esempio aneddotico, nel 1979 la SEC (Securities and Exchange Commission), l’agenzia statunitense incaricata di regolamentare i mercati finanziari, introdusse la sua famosa Regola 156. Questa regola richiede ai gestori di fondi di informare gli investitori che la performance passata non è indicativa dei risultati futuri. La performance passata è implicitamente il “modello” di cui la SEC avverte di non fidarsi per il suo potere di “generalizzazione”; cioè, la sua capacità di predire qualsiasi cosa sul futuro.
Anche la scienza stessa fatica a definire cosa significhi estrapolare la “verità” al di fuori di un ristretto insieme di osservazioni. Gli scandali della “bad science”, che si sono svolti negli anni 2000 e 2010 attorno al p-hacking, indicano che interi campi di ricerca sono compromessi e non possono essere considerati affidabili2. Pur essendoci casi di frode evidente in cui i dati sperimentali sono stati palesemente manipolati, nella maggior parte dei casi, il nocciolo del problema risiede nei modelli; vale a dire, nel processo intellettuale utilizzato per generalizzare quanto è stato osservato.
Nel suo aspetto più ampio, il problema della generalizzazione è indistinguibile da quello della scienza stessa, ed è quindi difficile quanto replicare l’ampiezza dell’ingegno e del potenziale umano. Tuttavia, l’aspetto più ristretto e statistico del problema della generalizzazione è molto più affrontabile, ed è questa la prospettiva che verrà adottata nelle sezioni successive.
L’emergere di una nuova scienza
La generalizzazione emerse come paradigma statistico all’inizio del XX secolo, principalmente attraverso la lente dell’accuratezza delle previsioni3, che rappresenta un caso speciale strettamente legato alle previsioni di serie temporali. Nei primi anni del 1900, l’emergere di una classe media proprietaria di azioni negli Stati Uniti suscitò un enorme interesse per metodi che aiutassero le persone a garantire ritorni finanziari sui beni negoziati. Indovini e previsori economici si degnarono di estrapolare eventi futuri per un pubblico disposto a pagare con entusiasmo. Si sono fatte e perse fortune, ma tali sforzi hanno offerto ben poco chiarimento sul modo “corretto” di affrontare il problema.
La generalizzazione è rimasta, per lo più, un problema sconcertante per la maggior parte del XX secolo. Non era nemmeno chiaro se appartenesse al regno delle scienze naturali, governato da osservazioni e sperimentazioni, o a quello della filosofia e della matematica, governato dalla logica e dalla coerenza interna.
Il percorso proseguì fino a un momento storico nel 1982, l’anno della prima competizione di previsioni pubblica - colloquialmente nota come la competizione M4. Il principio era semplice: pubblicare un dataset di 1000 serie temporali troncate, lasciare che i partecipanti inviatessero le loro previsioni e, infine, pubblicare il resto del dataset (le code troncate) insieme alle rispettive accuratezze ottenute dai partecipanti. Con questa competizione, la generalizzazione, ancora vista attraverso la lente dell’accuratezza delle previsioni, era entrata nel regno delle scienze naturali. In seguito, le competizioni di previsioni divennero sempre più frequenti.
Alcuni decenni dopo, Kaggle, fondata nel 2010, aggiunse una nuova dimensione a tali competizioni creando una piattaforma dedicata ai problemi di previsione generale (non solo alle serie temporali). A febbraio 20235, la piattaforma ha organizzato 349 competizioni con premi in denaro. Il principio rimane lo stesso della competizione M originale: viene reso disponibile un dataset troncato, i concorrenti inviano le loro risposte ai compiti di previsione assegnati e, infine, vengono rivelate le classifiche insieme alla porzione nascosta del dataset. Le competizioni sono ancora considerate il punto di riferimento per una valutazione corretta dell’errore di generalizzazione dei modelli.
Overfitting e underfitting
Overfitting, come il suo opposto underfitting, è un problema che frequentemente sorge durante la creazione di un modello basato su un dataset fornito, e compromette il potere di generalizzazione del modello. Storicamente6, l’overfitting emerse come il primo ostacolo ben compreso alla generalizzazione.
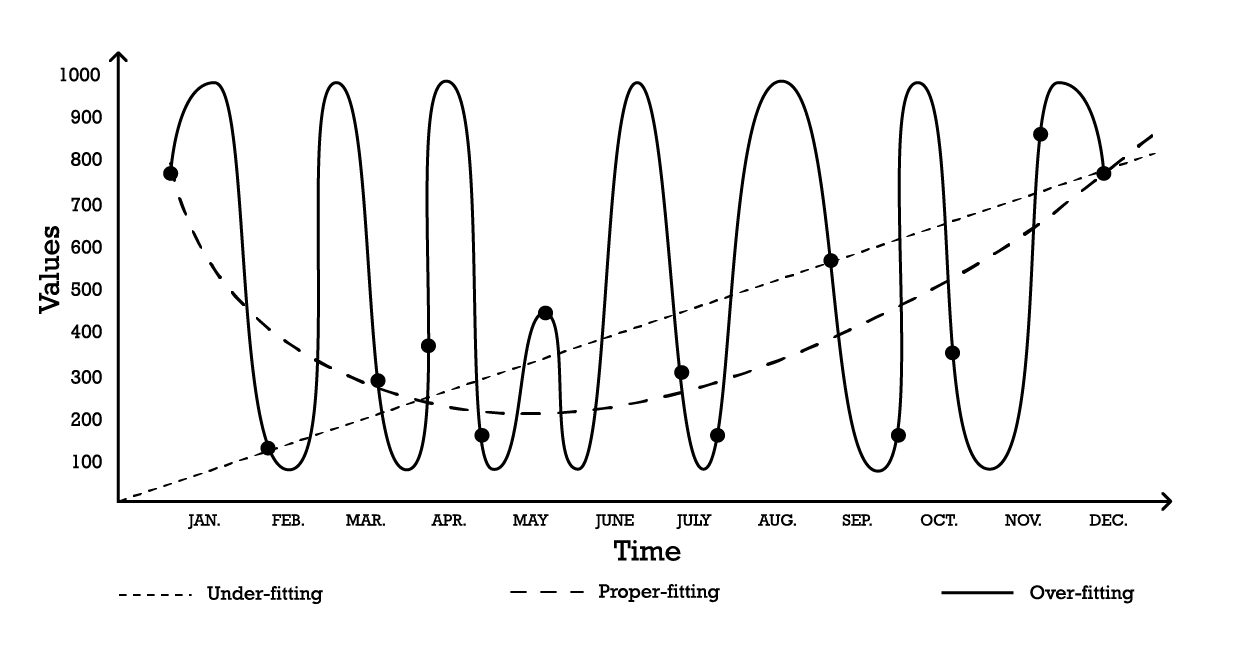
La visualizzazione dell overfitting può essere realizzata utilizzando un semplice problema di modellazione di serie temporali. Ai fini di questo esempio, supponiamo che l’obiettivo sia creare un modello che rifletta una serie di osservazioni storiche. Una delle opzioni più semplici per modellare queste osservazioni è un modello lineare, come illustrato di seguito (vedi Figura 1).

Figura 1: Un grafico composito che raffigura tre diversi tentativi di 'adattare' una serie di osservazioni.
Con due parametri, il modello di “under-fitting” è robusto, ma, come suggerisce il nome, underfits i dati, poiché non riesce chiaramente a cogliere la forma complessiva della distribuzione delle osservazioni. Questo approccio lineare ha un bias elevato ma una varianza bassa. In questo contesto, il bias dovrebbe essere inteso come la limitazione intrinseca della strategia di modellazione nel catturare i dettagli delle osservazioni, mentre la varianza indica la sensibilità a piccole fluttuazioni – possibilmente rumore – delle osservazioni.
Un modello abbastanza complesso potrebbe essere adottato, secondo la curva di “over-fitting” (Figura 1). Questo modello include molti parametri e si adatta esattamente alle osservazioni. Questo approccio ha un bias basso ma una varianza dimostrabilmente elevata. In alternativa, si potrebbe adottare un modello di complessità intermedia, come si vede nella curva di “proper-fitting” (Figura 1). Questo modello include tre parametri, presenta un bias medio e una varianza media. Tra queste tre opzioni, il modello di proper-fitting è invariabilmente quello che offre le migliori prestazioni in termini di generalizzazione.
Queste opzioni di modellazione rappresentano l’essenza del compromesso bias-varianza.7 8 Il compromesso bias-varianza è un principio generale che stabilisce come il bias possa essere ridotto aumentando la varianza. L’errore di generalizzazione viene minimizzato trovando il giusto equilibrio tra la quantità di bias e di varianza.
Storicamente, dall’inizio del XX secolo fino ai primi anni 2010, un modello overfitted veniva definito9 come uno che conteneva più parametri di quanti possano essere giustificati dai dati. Infatti, a prima vista, aggiungere troppe libertà a un modello sembra essere la ricetta perfetta per i problemi di overfitting. Tuttavia, l’emergere del deep learning ha dimostrato che questa intuizione, e la definizione di overfitting, erano fuorvianti. Questo punto verrà rivisitato nella sezione sul deep double-descent.
Validazione incrociata e backtesting
La validazione incrociata è una tecnica di validazione del modello utilizzata per valutare quanto bene un modello riesca a generalizzare al di là del dataset di supporto. Si tratta di un metodo di sottocampionamento che utilizza diverse porzioni dei dati per testare e addestrare un modello in iterazioni differenti. La validazione incrociata è il fondamento delle pratiche predittive moderne, e quasi tutti i partecipanti vincenti ai concorsi di previsione fanno ampio uso di questa tecnica.
Esistono numerose varianti della validazione incrociata. La variante più popolare è la validazione k-fold, in cui il campione originale viene partizionato casualmente in k sottocampioni. Ogni sottocampione viene utilizzato una volta come dati di validazione, mentre il resto – tutti gli altri sottocampioni – viene utilizzato come dati di addestramento.
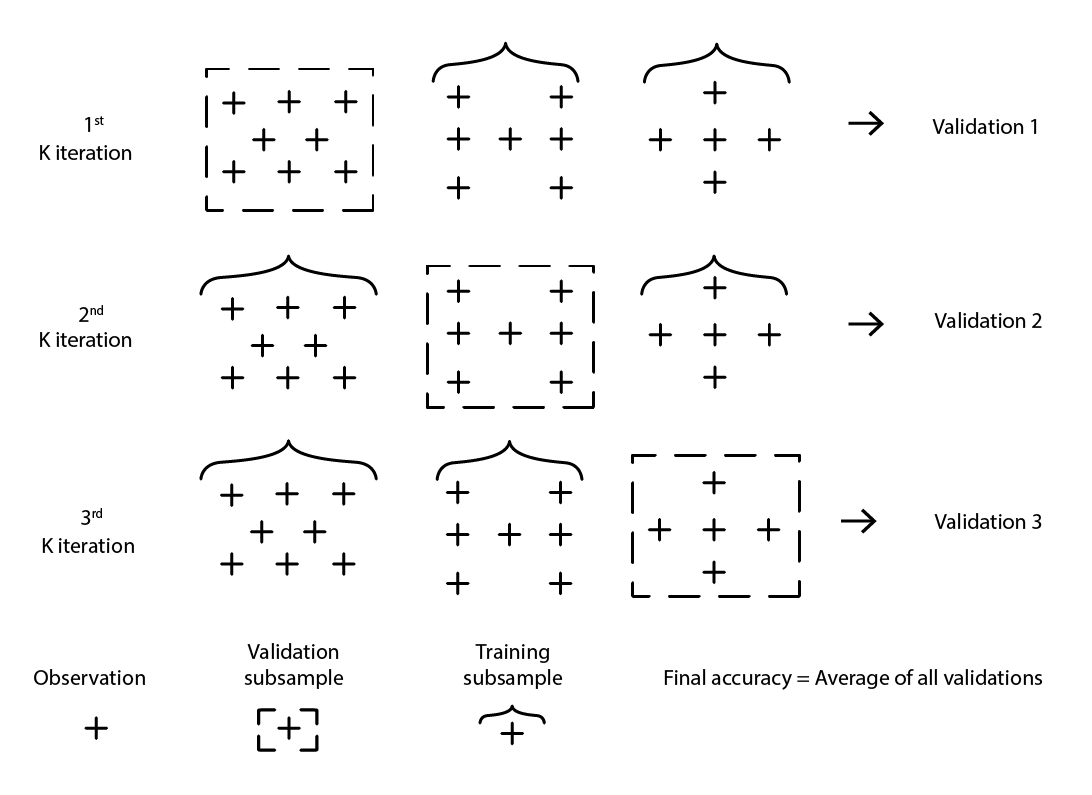
Figura 2: Un esempio di validazione k-fold. Le osservazioni sopra provengono tutte dallo stesso dataset. La tecnica, quindi, costruisce sottocampioni di dati ad uso di validazione e addestramento.
La scelta del valore k, ovvero il numero di sottocampioni, rappresenta un compromesso tra i guadagni statistici marginali e le risorse computazionali richieste. Infatti, con la validazione k-fold, le risorse computazionali crescono linearmente con il valore k, mentre i benefici, in termini di riduzione dell’errore, sperimentano rendimenti decrescenti estremi10. In pratica, selezionare un valore di 10 o 20 per k è solitamente “abbastanza buono”, poiché i guadagni statistici associati a valori più alti non giustificano l’inconveniente aggiuntivo legato al maggiore impiego di risorse computazionali.
La validazione incrociata presume che il dataset possa essere scomposto in una serie di osservazioni indipendenti. Tuttavia, nella supply chain, ciò non è frequentemente il caso, poiché il dataset solitamente riflette dati storicizzati in cui è presente una dipendenza temporale. In presenza del tempo, il sottocampione di addestramento deve essere rigorosamente posto come “precedente” a quello di validazione. In altre parole, il “futuro”, relativo al cutoff del campionamento, non deve trapelare nel sottocampione di validazione.
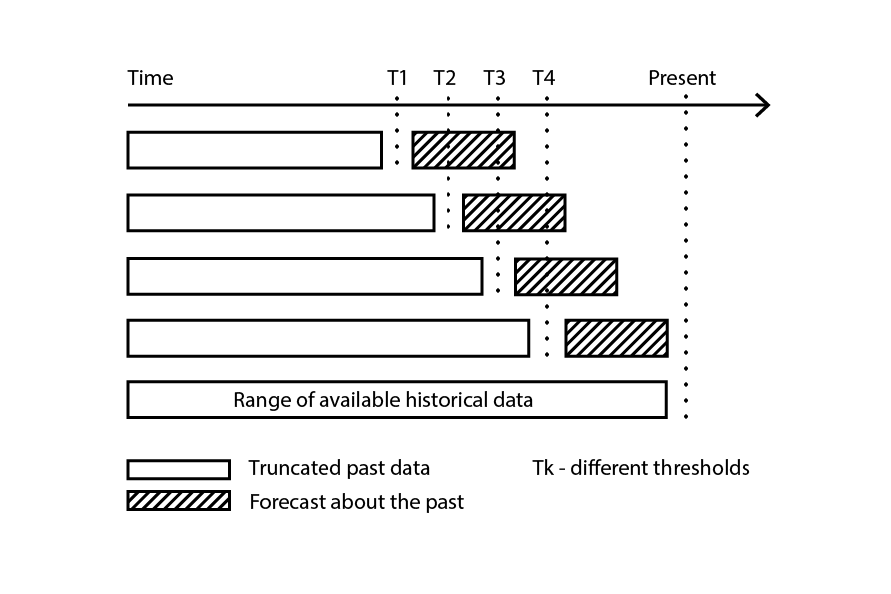
Figura 3: Un esempio di processo di backtesting che costruisce sottocampioni di dati per scopi di validazione e addestramento.
Backtesting rappresenta la variante della validazione incrociata che affronta direttamente la dipendenza temporale. Invece di considerare sottocampioni casuali, i dati di addestramento e di validazione vengono rispettivamente ottenuti tramite un cutoff: le osservazioni antecedenti al cutoff appartengono ai dati di addestramento, mentre quelle successive appartengono ai dati di validazione. Il processo viene iterato scegliendo una serie di cutoff distinti.
Il metodo di campionamento che sta alla base sia della validazione incrociata sia del backtesting è un meccanismo potente per indirizzare lo sforzo di modellazione verso una maggiore generalizzazione. Infatti, è così efficiente che esiste un’intera classe di algoritmi di (machine) learning che abbraccia questo stesso meccanismo alla loro base. I più notevoli sono le random forests e le gradient boosted trees.
Superare la barriera dimensionale
È naturale che, più dati si possiedono, maggiore sia l’informazione da apprendere. Quindi, a parità di condizioni, più dati dovrebbero portare a modelli migliori, o comunque a modelli non peggiori dei loro predecessori. Dopotutto, se più dati peggiorassero il modello, sarebbe sempre possibile ignorarli come ultima risorsa. Tuttavia, a causa dei problemi di overfitting, abbandonare i dati è rimasta la soluzione del minore dei mali fino alla fine degli anni ‘90. Questo era il nocciolo del problema della “barriera dimensionale”. Una situazione al contempo sconcertante e profondamente insoddisfacente. Le scoperte rivoluzionarie degli anni ‘90 abbatterono le barriere dimensionali con intuizioni stupefacenti, sia teoriche che pratiche. Nel processo, tali scoperte riuscirono a sconvolgere – per puro effetto di distrazione – l’intero campo di studio per un decennio, ritardando l’avvento dei suoi successori, principalmente i metodi di deep learning, discussi nella sezione successiva.
Per comprendere meglio ciò che in passato era considerato problematico nell’aver più dati, consideriamo il seguente scenario: un produttore fittizio desidera prevedere il numero di riparazioni non programmate per anno su grandi impianti industriali. Dopo un’attenta analisi del problema, il team di ingegneria ha identificato tre fattori indipendenti che sembrano contribuire ai tassi di guasto. Tuttavia, il contributo rispettivo di ciascun fattore nel tasso complessivo di guasto non è chiaro.
Pertanto, viene introdotto un semplice modello di regressione lineare con 3 variabili di input. Il modello può essere scritto come Y = a1 * X1 + a2 * X2 + a3 * X3, dove
-
Y è l’output del modello lineare (il tasso di guasto che gli ingegneri desiderano prevedere)
-
X1, X2 e X3 sono i tre fattori (tipologie specifiche di carichi di lavoro espressi in ore di funzionamento) che possono contribuire ai guasti
-
a1, a2 e a3 sono i tre parametri del modello che devono essere identificati. Il numero di osservazioni necessario per ottenere stime “abbastanza buone” per i tre parametri dipende in gran parte dal livello di rumore presente nell’osservazione e da cosa si intenda per “abbastanza buono”. Tuttavia, intuitivamente, per adattare tre parametri servirebbero almeno due dozzine di osservazioni anche nelle situazioni più favorevoli. Poiché gli ingegneri riescono a raccogliere 100 osservazioni, riescono a regredire 3 parametri, e il modello risultante sembra “abbastanza buono” da essere di interesse pratico. Il modello non riesce a catturare molti aspetti delle 100 osservazioni, rendendolo un’approssimazione molto grezza, ma quando questo modello viene messo alla prova in altre situazioni attraverso esperimenti mentali, l’intuizione e l’esperienza dicono agli ingegneri che il modello sembra comportarsi in modo ragionevole.
In seguito al loro primo successo, gli ingegneri decidono di approfondire ulteriormente. Questa volta, sfruttano l’intera gamma di sensori elettronici integrati nelle macchine e, attraverso i registri elettronici prodotti da tali sensori, riescono ad aumentare il set di fattori d’ingresso a 10.000. Inizialmente, il dataset era composto da 100 osservazioni, con ciascuna osservazione caratterizzata da 3 numeri. Ora, il dataset è stato ampliato; sono ancora le stesse 100 osservazioni, ma ci sono 10.000 numeri per osservazione.
Tuttavia, mentre gli ingegneri cercano di applicare lo stesso approccio al loro dataset enormemente arricchito, il modello lineare non funziona più. Poiché ci sono 10.000 dimensioni, il modello lineare comporta 10.000 parametri; e le 100 osservazioni sono ben al di sotto del necessario per supportare la regressione di così tanti parametri. Il problema non è che sia impossibile trovare valori di parametri che si adattino, ma esattamente il contrario: è diventato banale trovare insiemi infiniti di parametri che si adattano perfettamente alle osservazioni. Eppure, nessuno di questi modelli “adattati” è di alcun uso pratico. Questi modelli “grandi” si adattano perfettamente alle 100 osservazioni; tuttavia, al di fuori di quelle osservazioni, i modelli diventano insensati.
Gli ingegneri si trovano di fronte alla barriera dimensionale: a quanto pare, il numero di parametri deve rimanere piccolo rispetto alle osservazioni, altrimenti lo sforzo di modellazione crolla. Questo problema è fastidioso poiché il dataset “più grande”, con 10.000 dimensioni anziché 3, è ovviamente più informativo di quello più piccolo. Pertanto, un modello statistico adeguato dovrebbe riuscire a catturare queste informazioni extra invece di diventare disfunzionale quando ne viene a contatto.
A metà degli anni ‘90, una svolta duplice11, sia teorica che sperimentale, ha fatto scalpore nella comunità. La svolta teorica fu la teoria Vapnik–Chervonenkis (VC)12. La teoria VC ha dimostrato che, considerando tipi specifici di modelli, l’errore reale poteva essere limitato superiormente da quella che vagamente equivaleva alla somma dell’errore empirico più il rischio strutturale, una proprietà intrinseca del modello stesso. In questo contesto, “errore reale” è l’errore riscontrato sui dati che non si hanno, mentre “errore empirico” è l’errore riscontrato sui dati che si hanno. Minimizzando la somma dell’errore empirico e del rischio strutturale, l’errore reale poteva essere minimizzato, in quanto era “incastrato”. Ciò rappresentava un risultato sorprendente e, probabilmente, il più grande passo verso la generalizzazione dalla stessa identificazione del problema di overfitting.
Sul fronte sperimentale, furono introdotti i modelli in seguito noti come Support Vector Machines (SVMs) quasi come una derivazione da manuale di ciò che la teoria VC aveva individuato sull’apprendimento. Questi SVM sono diventati i primi modelli di successo in grado di sfruttare in modo soddisfacente i dataset in cui il numero di dimensioni superava il numero di osservazioni.
Inquadrando l’errore reale, un risultato teorico veramente sorprendente, la teoria VC aveva infranto la barriera dimensionale - qualcosa che era rimasto problematico per quasi un secolo. Ha anche aperto la strada a modelli capaci di sfruttare dati ad alta dimensionalità. Eppure, ben presto, gli SVM furono a loro volta superati da modelli alternativi, principalmente metodi ensemble (random forests13 e gradient boosting), che si rivelarono, all’inizio degli anni 2000, alternative superiori14, prevalendo sia sulla generalizzazione che sui requisiti computazionali. Come gli SVM che hanno sostituito, i metodi ensemble beneficiano anche di garanzie teoriche riguardo alla loro capacità di evitare l’overfitting. Tutti questi metodi condividevano la proprietà di essere metodi non parametrici. La barriera dimensionale era stata infranta grazie all’introduzione di modelli che non dovevano introdurre uno o più parametri per ogni dimensione, evitando così un noto percorso verso i problemi dell’overfitting.
Ritornando al problema delle riparazioni non programmate menzionato in precedenza, a differenza dei modelli statistici classici – come la regressione lineare, che crolla di fronte alla barriera dimensionale – i metodi ensemble riuscirebbero a trarre vantaggio dal grande dataset e dalle sue 10.000 dimensioni, nonostante ci siano solo 100 osservazioni. Inoltre, i metodi ensemble eccellerebbero più o meno direttamente dalla scatola. Operativamente, questo fu uno sviluppo notevole, in quanto eliminava la necessità di elaborare meticolosamente i modelli selezionando il set esattamente corretto di dimensioni d’ingresso.
L’impatto sulla comunità in senso lato, sia all’interno che all’esterno del mondo accademico, fu enorme. La maggior parte degli sforzi di ricerca degli inizi degli anni 2000 era dedicata all’esplorazione di questi approcci non parametrici “supportati dalla teoria”. Eppure, i successi svanirono piuttosto rapidamente con il passare degli anni. Infatti, a quasi vent’anni di distanza, i migliori modelli da quella che divenne nota come prospettiva del statistical learning rimangono gli stessi, beneficiando semplicemente di implementazioni più performanti15.
Il deep double-descent
Fino al 2010, il pensiero convenzionale dettava che, per evitare problemi di overfitting, il numero di parametri dovesse rimanere molto inferiore al numero di osservazioni. Infatti, poiché ogni parametro rappresentava implicitamente un grado di libertà, avere tanti parametri quante osservazioni era una ricetta sicura per l’overfitting16. I metodi ensemble aggiravano completamente il problema essendo non parametrici fin dall’inizio. Eppure, questa intuizione critica si è rivelata errata, e in modo spettacolare.
Quello che in seguito divenne noto come approccio del deep learning ha sorpreso quasi tutta la comunità attraverso modelli iperparametrici. Questi sono modelli che non presentano overfitting e contengono molte volte più parametri rispetto alle osservazioni.
La genesi del deep learning è complessa e può essere fatta risalire ai primi tentativi di modellare i processi del cervello, ovvero le reti neurali. Analizzare in dettaglio questa genesi è al di fuori dello scopo della presente trattazione, tuttavia, vale la pena notare che la rivoluzione del deep learning dei primi anni 2010 è iniziata proprio quando il settore ha abbandonato la metafora della rete neurale a favore della mechanical sympathy. Le implementazioni del deep learning hanno sostituito i modelli precedenti con varianti molto più semplici. Questi nuovi modelli hanno sfruttato hardware di calcolo, in particolare le GPU (unità di elaborazione grafica), che si sono dimostrate, in maniera in qualche modo accidentale, ben adatte alle operazioni di algebra lineare che caratterizzano i modelli di deep learning17.
Ci sono voluti quasi altri cinque anni affinché il deep learning fosse ampiamente riconosciuto come una svolta. Una parte consistente della reticenza proveniva dal campo del statistical learning - coincidentemente, quella parte della comunità che aveva rotto con successo la barriera dimensionale due decenni prima. Sebbene le spiegazioni per questa reticenza varino, la apparente contraddizione tra la saggezza convenzionale sull’overfitting e le affermazioni sul deep learning ha certamente contribuito a un livello apprezzabile di iniziale scetticismo riguardo a questa nuova classe di modelli.
La contraddizione rimase in gran parte irrisolta fino al 2019, quando fu identificato il deep double descent18, un fenomeno che caratterizza il comportamento di certe classi di modelli. Per tali modelli, l’aumento del numero di parametri inizialmente degrada l’errore di test (attraverso l’overfitting), fino a quando il numero di parametri diventa sufficientemente grande da invertire la tendenza e migliorare nuovamente l’errore di test. La “seconda discesa” (dell’errore di test) non era un comportamento previsto dalla prospettiva del tradeoff bias-variance.
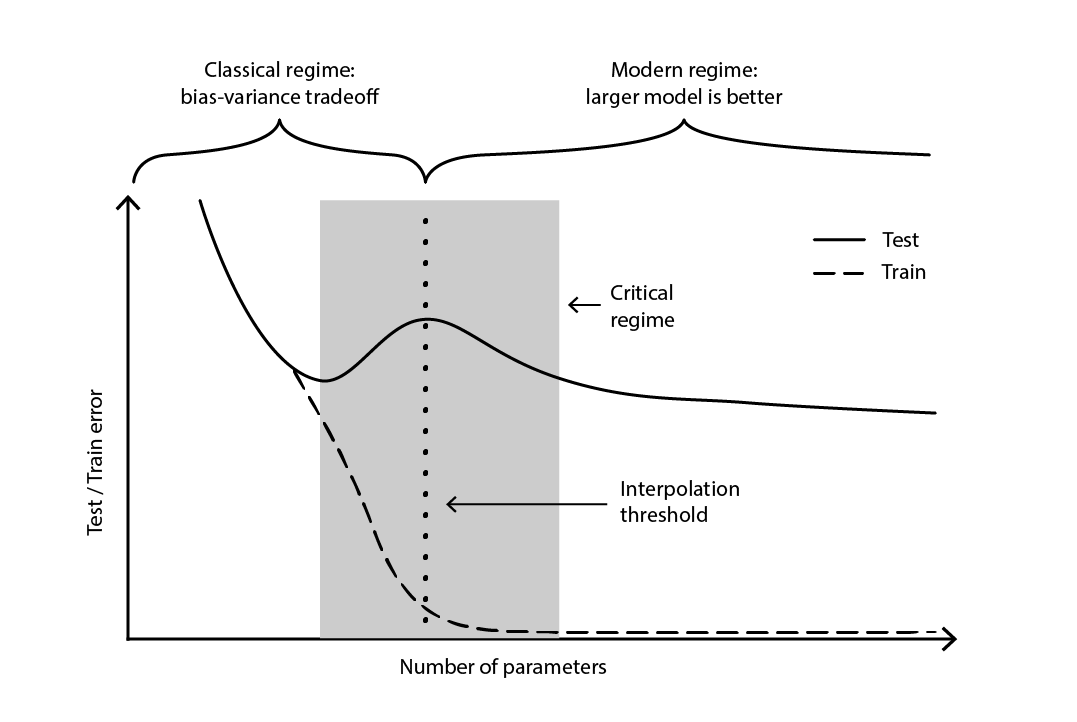
Figura 4. Un deep double descent.
La Figura 4 illustra i due regimi successivi descritti sopra. Il primo regime è il classico compromesso bias-variance che sembra portare a un numero “ottimale” di parametri. Tuttavia, questo minimo si rivela essere un minimo locale. Esiste un secondo regime, osservabile se si continua ad aumentare il numero di parametri, che mostra una convergenza asintotica verso un vero errore di test ottimale per il modello.
Il deep double descent non solo ha conciliato le prospettive statistica e del deep learning, ma ha anche dimostrato che la generalizzazione rimane relativamente poco compresa. Ha provato che le teorie ampiamente diffuse – comuni fino alla fine degli anni 2010 – presentavano una prospettiva distorta sulla generalizzazione. Tuttavia, il deep double descent non fornisce ancora un quadro di riferimento – o qualcosa di equivalente – che possa prevedere le capacità di generalizzazione (o la loro mancanza) dei modelli in base alla loro struttura. Ad oggi, l’approccio rimane decisamente empirico.
Le spine della supply chain
Come ampiamente esposto, la generalizzazione è estremamente difficile, e le supply chain riescono a imprecare la situazione con le loro peculiarità, intensificandola ulteriormente. Innanzitutto, i dati che i professionisti della supply chain cercano potrebbero rimanere per sempre inaccessibili; non solo parzialmente invisibili, ma del tutto non osservabili. In secondo luogo, l’atto stesso di predire potrebbe alterare il futuro, e la validità della predizione, dato che le decisioni sono basate su quelle stesse predizioni. Pertanto, nell’affrontare la generalizzazione in un contesto di supply chain, si dovrebbe utilizzare un approccio a due falde; una basata sulla solidità statistica del modello e l’altra sul ragionamento ad alto livello che lo supporta.
Inoltre, i dati disponibili non sono sempre i dati desiderati. Consideriamo un produttore che vuole prevedere la domanda al fine di decidere le quantità da produrre. Non esistono dati storici sulla “domanda”. Invece, i dati storici delle vendite rappresentano il miglior proxy disponibile per il produttore per riflettere la domanda storica. Tuttavia, le vendite storiche sono distorte da passati stock-outs. Le vendite pari a zero, causate dagli stock-outs, non dovrebbero essere confuse con una domanda pari a zero. Sebbene sia possibile realizzare un modello per rettificare questa storia delle vendite in una sorta di storia della domanda, l’errore di generalizzazione di questo modello è elusivo per sua natura, poiché né il passato né il futuro contengono tali dati. In breve, la “domanda” è un costrutto necessario ma intangibile.
Nel gergo del machine learning, modellare la domanda è un problema di apprendimento non supervisionato in cui l’output del modello non viene mai osservato direttamente. Questo aspetto non supervisionato mette in difficoltà la maggior parte degli algoritmi di apprendimento e la maggior parte delle tecniche di validazione dei modelli – almeno, nella loro forma “naïve”. Inoltre, sminuisce l’idea stessa di prediction competition, intesa qui come un semplice processo in due fasi in cui un dataset originale viene suddiviso in una parte pubblica (training) e una parte privata (validation). La validazione stessa diventa, per necessità, un esercizio di modellazione.
In breve, la previsione creata dal produttore plasmerà, in un modo o nell’altro, il futuro che il produttore vivrà. Una domanda prevista elevata significa che il produttore aumenterà la produzione. Se l’azienda è ben gestita, è probabile che nel processo produttivo si raggiungano economie di scala, abbassando così i costi di produzione. A sua volta, il produttore probabilmente sfrutterà queste nuove economie per abbassare i prezzi, ottenendo così un vantaggio competitivo rispetto ai rivali. Il mercato, alla ricerca dell’opzione a prezzo più basso, potrebbe adottare rapidamente questo produttore come la sua opzione più competitiva, scatenando così un’impennata della domanda ben oltre la previsione iniziale.
Questo fenomeno è noto come profezia che si autoavvera, una previsione che tende a diventare vera in virtù della convinzione influente che i partecipanti ripongono in essa. Una prospettiva non ortodossa, ma non del tutto irragionevole, potrebbe caratterizzare le supply chain come gigantesche macchine autoavveranti alla Rube Goldberg. A livello metodologico, questo intreccio tra osservatore e osservazione complica ulteriormente la situazione, poiché la generalizzazione diventa associata alla cattura dell’intento strategico che sta alla base degli sviluppi della supply chain.
A questo punto, la sfida della generalizzazione, così come si presenta nella supply chain, potrebbe sembrare insormontabile. I fogli di calcolo, che restano ubiquitari nelle supply chain, suggeriscono certamente che questa sia la posizione predefinita, seppur implicita, della maggior parte delle aziende. Un foglio di calcolo è, tuttavia, prima di tutto uno strumento per rimandare la risoluzione del problema a un giudizio umano ad hoc, piuttosto che l’applicazione di un metodo sistematico.
Anche se affidarsi al giudizio umano è invariabilmente la risposta scorretta (di per sé), non è nemmeno una risposta soddisfacente al problema. La presenza degli stock-outs non significa che per la domanda si possa applicare un principio del tipo tutto vale. Certamente, se il produttore ha mantenuto livelli medi di service levels superiori al 90% negli ultimi tre anni, sarebbe altamente improbabile che la domanda (osservata) potesse essere dieci volte superiore alle vendite. Pertanto, è ragionevole aspettarsi che possa essere ingegnerizzato un metodo sistematico per far fronte a tali distorsioni. Allo stesso modo, la profezia che si autoavvera può essere modellata, in particolare attraverso la nozione di policy come intesa dalla teoria dei controlli.
Pertanto, quando si considera una supply chain reale, la generalizzazione richiede un approccio a due gambe. Innanzitutto, il modello deve essere statisticamente solido, nella misura consentita dalle ampie scienze dell’“apprendimento”. Ciò comprende non solo prospettive teoriche come la statistica classica e il statistical learning, ma anche sforzi empirici come il machine learning e le prediction competition. Ritornare alla statistica del XIX secolo non è una proposta ragionevole per una pratica della supply chain del XXI secolo.
Secondo, il modello deve essere supportato da un ragionamento di alto livello. In altre parole, per ogni componente del modello e per ogni fase del processo di modellazione, ci dovrebbe essere una giustificazione che abbia senso dal punto di vista della supply chain. Senza questo ingrediente, il caos operativo19 è quasi garantito, di solito innescato da un’evoluzione della supply chain stessa, del suo ecosistema operativo o del suo paesaggio applicativo sottostante. Infatti, l’intero scopo del ragionamento di alto livello non è far funzionare un modello una volta sola, ma farlo operare in modo sostenibile per diversi anni in un ambiente in continua evoluzione. Questo ragionamento è l’ingrediente non così segreto che aiuta a decidere quando è il momento di rivedere il modello, quando il suo design, qualunque esso sia, non si allinea più con la realtà e/o con gli obiettivi aziendali.
Da lontano, questa proposta potrebbe sembrare vulnerabile alla critica già rivolta ai fogli di calcolo – quella contro il delegare il duro lavoro a un elusivo “giudizio umano”. Sebbene questa proposta rimandi ancora la valutazione del modello al giudizio umano, l’esecuzione del modello è concepita come completamente automatizzata. Pertanto, le operazioni quotidiane sono intese per essere completamente automatizzate, anche se gli sforzi ingegneristici in corso per migliorare ulteriormente le ricette numeriche non lo sono.
Note
-
Esiste una tecnica algoritmica importante chiamata “memoization” che sostituisce precisamente un risultato che potrebbe essere riconcomputato con il suo risultato pre-calcolato, scambiando così più memoria per meno calcolo. Tuttavia, questa tecnica non è rilevante per la presente discussione. ↩︎
-
Why Most Published Research Findings Are False, John P. A. Ioannidis, Agosto 2005 ↩︎
-
Dal punto di vista delle previsioni delle serie temporali, la nozione di generalizzazione viene affrontata tramite il concetto di “accuratezza”. L’accuratezza può essere vista come un caso particolare della “generalizzazione” quando si considerano le serie temporali. ↩︎
-
Makridakis, S.; Andersen, A.; Carbone, R.; Fildes, R.; Hibon, M.; Lewandowski, R.; Newton, J.; Parzen, E.; Winkler, R. (Aprile 1982). “L’accuratezza dei metodi di estrapolazione (serie temporali): Risultati di una competizione di previsione”. Journal of Forecasting. 1 (2): 111–153. doi:10.1002/for.3980010202. ↩︎
-
Kaggle in Numbers, Carl McBride Ellis, recuperato l'8 febbraio 2023, ↩︎
-
L’estratto del 1935 “Forse siamo un po’ antiquati, ma per noi un’analisi a sei variabili basata su tredici osservazioni sembra piuttosto un overfitting”, tratto da “The Quarterly Review of Biology” (settembre 1935, Volume 10, Numero 3, pp. 341 – 377), sembra indicare che il concetto statistico di overfitting era già stato stabilito a quel tempo. ↩︎
-
Grenander, Ulf. On empirical spectral analysis of stochastic processes. Ark. Mat., 1(6):503–531, 08 1952. ↩︎
-
Whittle, P. Tests of Fit in Time Series, Vol. 39, No. 3/4 (dicembre 1952), pp. 309-318] (10 pagine), Oxford University Press ↩︎
-
Everitt B.S., Skrondal A. (2010), Cambridge Dictionary of Statistics, Cambridge University Press. ↩︎
-
I benefici asintotici dell’utilizzo di valori maggiori di k per il k-fold possono essere dedotti dal teorema del limite centrale. Questo spunto suggerisce che, aumentando k, possiamo avvicinarci approssimativamente a 1 / sqrt(k) dall’esaurimento del potenziale di miglioramento offerto dal k-fold in origine. ↩︎
-
Support-vector networks, Corinna Cortes, Vladimir Vapnik, Machine Learning, volume 20, pagine 273–297 (1995) ↩︎
-
La teoria Vapnik-Chervonenkis (VC) non è stata l’unica candidata a formalizzare il significato di “learning”. Il framework PAC (probably approximately correct) di Valiant del 1984 ha aperto la strada agli approcci formali all’apprendimento. Tuttavia, il framework PAC non ha ottenuto l’immensa trazione e i successi operativi che la teoria VC ha riscontrato intorno al millennio. ↩︎
-
Random Forests, Leo Breiman, Machine Learning, volume 45, pagine 5–32 (2001) ↩︎
-
Una delle sfortunate conseguenze del fatto che le Support Vector Machines (SVMs) siano fortemente ispirate da una teoria matematica è che tali modelli mostrano poca “simpatia meccanica” per l’hardware informatico moderno. L’inadeguatezza relativa delle SVM nel processare grandi dataset – inclusi milioni di osservazioni o più – rispetto ad alternative ha segnato il declino di tali metodi. ↩︎
-
XGBoost e LightGBM sono due implementazioni open-source dei metodi ensemble che rimangono ampiamente popolari all’interno dei circoli del machine learning. ↩︎
-
Per ragioni di sintesi, qui si sta procedendo con una certa eccessiva semplificazione. Esiste un intero campo di ricerca dedicato alla “regolarizzazione” dei modelli statistici. In presenza di vincoli di regolarizzazione, il numero di parametri, anche considerando un modello classico come la regressione lineare, può tranquillamente superare il numero delle osservazioni. In presenza di regolarizzazione, nessun valore del parametro rappresenta più un intero grado di libertà, bensì una frazione di esso. Pertanto, sarebbe più corretto parlare del numero di gradi di libertà, anziché del numero di parametri. Poiché queste considerazioni tangenziali non alterano fondamentalmente le idee presentate qui, la versione semplificata sarà sufficiente. ↩︎
-
In realtà, la causalità è inversa. I pionieri del deep learning sono riusciti a reingegnerizzare i loro modelli originali – le reti neurali – in modelli più semplici che si basavano quasi esclusivamente sull’algebra lineare. Lo scopo di questa reingegnerizzazione era proprio quello di rendere possibile l’esecuzione di questi nuovi modelli su hardware informatico che scambiava versatilità con pura potenza, vale a dire le GPU. ↩︎
-
Deep Double Descent: Where Bigger Models and More Data Hurt, Preetum Nakkiran, Gal Kaplun, Yamini Bansal, Tristan Yang, Boaz Barak, Ilya Sutskever, dicembre 2019 ↩︎
-
La stragrande maggioranza delle iniziative di data science nella supply chain fallisce. Le mie osservazioni casuali indicano che l’ignoranza del data scientist su ciò che fa funzionare la supply chain è la causa principale della maggior parte di questi fallimenti. Sebbene sia incredibilmente allettante – per un data scientist appena formato – sfruttare l’ultimo e più brillante pacchetto open-source di machine learning, non tutte le tecniche di modellazione sono altrettanto adatte a supportare un ragionamento di alto livello. Infatti, la maggior parte delle tecniche “mainstream” è decisamente pessima quando si tratta del processo di whiteboxing. ↩︎