00:19 Introduction
04:33 Deux définitions de l’algorithme
08:09 Big-O
13:10 L’histoire jusqu’à présent
15:11 Sciences auxiliaires (récapitulatif)
17:26 Algorithmes modernes
19:36 Surpasser l’optimalité
22:23 Structures de données - 1/4 - Liste
25:50 Structures de données - 2/4 - Arbre
27:39 Structures de données - 3/4 - Graphe
29:55 Structures de données - 4/4 - Table de hachage
31:30 Recettes magiques - 1/2
37:06 Recettes magiques - 2/2
39:17 Compréhensions de tenseurs - 1/3 - La notation ‘Einstein’
42:53 Compréhensions de tenseurs - 2/3 - La percée de l’équipe de Facebook
46:52 Compréhensions de tenseurs - 3/3 - Perspective supply chain
52:20 Techniques méta - 1/3 - Compression
56:11 Techniques méta - 2/3 - Mémorisation
58:44 Techniques méta - 3/3 - Immutabilité
01:03:46 Conclusion
01:06:41 Conférence suivante et questions du public
Description
L’optimisation des supply chains repose sur la résolution de nombreux problèmes numériques. Les algorithmes sont des numerical recipes hautement codifiés destinés à résoudre des problèmes computationnels précis. Des algorithmes supérieurs signifient que des résultats supérieurs peuvent être obtenus avec moins de ressources informatiques. En se concentrant sur les spécificités de supply chain, la performance algorithmique peut être grandement améliorée, parfois de plusieurs ordres de grandeur. Les algorithmes supply chain doivent également adopter la conception des ordinateurs modernes, qui a considérablement évolué au cours des dernières décennies.
Transcription intégrale

Bienvenue dans cette série de conférences sur la supply chain. Je suis Joannes Vermorel, et aujourd’hui je vais présenter “Modern Algorithms for Supply Chain.” Des capacités de calcul supérieures sont essentielles pour obtenir une supply chain performance supérieure. Des prévisions précises, une optimisation plus fine et une optimisation plus fréquente sont toutes souhaitables afin d’atteindre une performance supply chain supérieure. Il existe toujours une méthode numérique supérieure, juste un peu au-delà des ressources de calcul que vous pouvez vous permettre.
Les algorithmes, pour simplifier, font fonctionner les ordinateurs plus rapidement. Ils constituent une branche des mathématiques, et c’est un domaine de recherche très actif. Les progrès dans ce domaine dépassent fréquemment l’avancement du matériel informatique lui-même. L’objectif de cette conférence est de comprendre ce que sont les algorithmes modernes et, plus spécifiquement du point de vue supply chain, comment aborder les problèmes afin de tirer pleinement parti de ces algorithmes modernes pour votre supply chain.

En ce qui concerne les algorithmes, il existe un livre qui est une référence absolue : Introduction to Algorithms, publié pour la première fois en 1990. C’est un livre incontournable. La qualité de la présentation et de l’écriture est tout simplement exceptionnelle. Ce livre s’est vendu à plus d’un demi-million d’exemplaires au cours de ses 20 premières années et a inspiré toute une génération d’écrivains académiques. En fait, la plupart des livres récents sur la supply chain traitant de la théorie de supply chain publiés au cours de la dernière décennie se sont souvent fortement inspirés du style et de la présentation que l’on trouve dans ce livre.
Personnellement, j’ai lu ce livre en 1997, et c’était en fait une traduction française de la toute première édition. Il a eu une influence profonde sur toute ma carrière. Après avoir lu ce livre, je n’ai plus jamais vu les logiciels de la même manière. Un mot de prudence, cependant, est que ce livre adopte une perspective sur le matériel informatique qui prévalait à la fin des années 80 et au début des années 90. Comme nous l’avons vu dans les conférences précédentes de cette série, le matériel informatique a progressé de manière assez spectaculaire au cours des dernières décennies, et ainsi certaines des hypothèses faites dans ce livre semblent relativement dépassées. Par exemple, le livre suppose que les accès mémoires se font en temps constant, quelle que soit la quantité de mémoire que vous souhaitez adresser. Ce n’est plus ainsi que fonctionnent les ordinateurs modernes.
Néanmoins, je pense qu’il existe certaines situations où être simpliste est une proposition raisonnable si, en échange, vous gagnez un degré beaucoup plus élevé de clarté et de simplicité d’exposition. Ce livre excelle dans ce domaine. Bien que je conseille de garder à l’esprit que certaines des hypothèses clés formulées dans ce livre sont dépassées, il reste néanmoins une référence absolue que je recommanderais à l’ensemble du public.

Clarifions le terme « algorithm » pour le public qui n’est peut-être pas très familier avec cette notion. Il existe la définition classique selon laquelle il s’agit d’une séquence finie d’instructions informatiques bien définies. C’est le genre de définition que l’on trouve dans les manuels ou sur Wikipedia. Bien que la définition classique d’un algorithme ait ses mérites, je pense qu’elle laisse à désirer, car elle ne précise pas l’intention associée aux algorithmes. Il ne s’agit pas de n’importe quelle séquence d’instructions qui nous intéresse ; c’est une séquence très spécifique d’instructions informatiques. Ainsi, je propose une définition personnelle du terme algorithme : un algorithme est essentiellement une méthode logicielle de résolution de problèmes, granulée et axée sur la performance.
Décomposons cette définition, voulez-vous ? Tout d’abord, la partie de résolution de problèmes : un algorithme est complètement caractérisé par le problème qu’il s’efforce de résoudre. Sur cet écran, vous pouvez voir le pseudocode de l’algorithme Quicksort, qui est un algorithme populaire et bien connu. Quicksort cherche à résoudre le problème du tri, qui est le suivant : vous avez un tableau contenant des entrées de données, et vous souhaitez un algorithme qui renverra exactement le même tableau, mais avec toutes les entrées triées par ordre croissant. Les algorithmes s’attachent entièrement à un problème spécifique et bien défini.
Le second aspect concerne la manière dont vous jugez qu’un algorithme est meilleur. Un meilleur algorithme est celui qui vous permet de résoudre le même problème avec moins de ressources informatiques, ce qui signifie en pratique plus de rapidité. Enfin, il y a la partie granulaire. Quand nous parlons d’« algorithmes », cela implique l’idée que nous souhaitons examiner des problèmes très élémentaires, modulaires et pouvant être composés indéfiniment pour résoudre des problèmes bien plus compliqués. Voilà en quoi consistent vraiment les algorithmes.
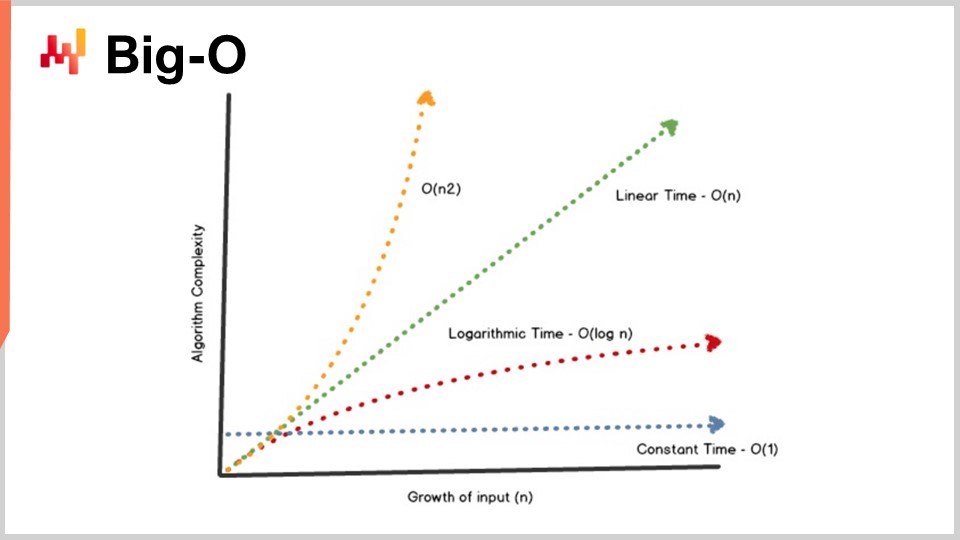
Une réalisation clé de la théorie des algorithmes est de fournir une caractérisation de la performance des algorithmes de manière assez abstraite. Je n’aurai pas le temps aujourd’hui d’approfondir les détails de cette caractérisation et du cadre mathématique. L’idée est que, pour caractériser l’algorithme, nous souhaitons examiner le comportement asymptotique. Nous avons un problème qui dépend d’une ou de plusieurs dimensions goulot d’étranglement clés qui caractérisent le problème. Par exemple, dans le problème de tri que j’ai présenté plus tôt, la dimension caractéristique est généralement le nombre d’éléments à trier. La question est : que se passe-t-il lorsque le tableau d’éléments à trier devient très grand ? Je vais appeler cette dimension caractéristique par le nombre “n” par convention.
Maintenant, j’ai cette notation, la notation Big O, que vous avez peut-être vue lorsque vous travaillez avec des algorithmes. Je vais simplement exposer quelques éléments pour vous donner une intuition de ce qui se passe. D’abord, prenons par exemple un ensemble de données, et nous voulons en extraire un indicateur statistique simple, comme une moyenne. Si je dis que j’ai un algorithme en Big O de 1, cela signifie que je suis capable de fournir une solution à ce problème (calcul de la moyenne) en temps constant, que l’ensemble de données soit petit ou grand. Le temps constant, ou Big O de 1, est une exigence absolue chaque fois que vous souhaitez réaliser quelque chose en temps réel dans le sens de la communication machine à machine. Si vous ne disposez pas de quelque chose en temps constant, il devient très difficile, parfois impossible, d’atteindre des performances en temps réel.
En général, un autre aspect clé des performances est le Big O de N. Le Big O de N signifie que la complexité de l’algorithme est strictement linéaire par rapport à la taille de l’ensemble de données concerné. C’est ce que vous obtenez lorsque vous disposez d’une implémentation efficace capable de résoudre le problème en ne lisant les données qu’une fois ou un nombre fixe de fois. La complexité en Big O de N est généralement uniquement compatible avec une exécution par lots. Si vous souhaitez quelque chose d’en ligne et en temps réel, vous ne pouvez pas avoir un algorithme qui parcourt l’ensemble des données, à moins de savoir que votre ensemble de données a une taille fixe.
Au-delà de la linéarité, on a le Big O de N au carré. Le Big O de N au carré est un cas très intéressant car c’est le point critique de l’explosion de la production. Cela signifie que la complexité croît de façon quadratique par rapport à la taille de l’ensemble de données, ce qui veut dire que si vous avez 10 fois plus de données, vos performances seront 100 fois pires. C’est généralement le genre de performance où vous ne verrez aucun problème lors du prototype parce que vous travaillez avec de petits ensembles de données. Vous ne verrez aucun problème lors de la phase de test car, encore une fois, vous travaillez avec de petits ensembles de données. Dès que vous passez en production, vous avez un logiciel complètement lent. Très fréquemment dans le monde des enterprise software, notamment dans celui des logiciels d’entreprise pour supply chain, la plupart des problèmes de performance abyssaux que vous pouvez observer sur le terrain sont en réalité causés par des algorithmes quadratiques qui n’avaient pas été identifiés. En conséquence, vous observez un comportement quadratique qui est tout simplement super lent. Ce problème n’a pas été identifié dès le départ parce que les ordinateurs modernes sont assez rapides, et N au carré n’est pas si mauvais tant que N reste relativement petit. Cependant, dès que vous traitez avec un ensemble de données à l’échelle de la production, cela fait vraiment mal.
Cette conférence est en réalité la deuxième conférence de mon quatrième chapitre dans cette série de conférences sur la supply chain. Dans le premier chapitre, le prologue, j’ai présenté ma vision de la supply chain à la fois comme domaine d’étude et comme pratique. Ce que nous avons vu, c’est que la supply chain est un vaste ensemble de problèmes épineux, par opposition aux problèmes simples. Les problèmes épineux ne peuvent pas être abordés par des méthodologies naïves parce que l’on retrouve des comportements adverses partout, et donc il faut y consacrer une grande attention méthodologique. La plupart des méthodes naïves échouent de manière assez spectaculaire. C’est exactement ce que j’ai fait dans le deuxième chapitre, qui est entièrement consacré aux méthodologies adaptées à l’étude des supply chains et à l’amélioration de la gestion de la supply chain. Le troisième chapitre, qui n’est pas encore complet, est essentiellement un zoom sur ce que j’appelle le « personnel supply chain », une méthodologie très spécifique qui se concentre sur les problèmes eux-mêmes plutôt que sur les solutions que nous pouvons envisager pour les résoudre. À l’avenir, j’alternerai entre le chapitre trois et le présent chapitre, qui concerne les sciences auxiliaires de supply chain.
Lors de la dernière conférence, nous avons vu que nous pouvions obtenir plus de capacités de calcul pour notre supply chain grâce à un matériel informatique meilleur et plus moderne. Aujourd’hui, nous abordons le problème sous un autre angle – nous recherchons plus de capacités de calcul parce que nous disposons d’un meilleur logiciel. C’est de cela dont traitent les algorithmes.

Un bref récapitulatif : les sciences auxiliaires constituent essentiellement une perspective sur la supply chain elle-même. La conférence d’aujourd’hui ne porte pas strictement sur la supply chain ; elle traite des algorithmes. Cependant, je pense qu’elle revêt une importance fondamentale pour la supply chain. La supply chain n’est pas une île ; les progrès qui peuvent être réalisés dans la supply chain dépendent grandement des avancées déjà accomplies dans d’autres domaines adjacents. Je fais référence à ces domaines comme étant les sciences auxiliaires de supply chain.
Je crois que la situation est très similaire à la relation entre les sciences médicales et la chimie au cours du 19e siècle. Au tout début du 19e siècle, les sciences médicales se souciaient bien peu de la chimie. La chimie était encore le petit nouveau du quartier et n’était pas considérée comme une proposition valable pour un véritable patient. Avance rapide jusqu’au 21e siècle, l’idée que vous puissiez être un excellent médecin tout en ne connaissant rien à la chimie serait jugée complètement absurde. Il est admis qu’être un excellent chimiste ne fait pas de vous un excellent médecin, mais il est généralement convenu que si vous ne connaissez rien à la chimie du corps, il vous est impossible d’être compétent du point de vue des sciences médicales modernes. Mon opinion pour l’avenir est que, durant le 21e siècle, le domaine de la supply chain commencera à considérer le domaine des algorithmes de presque la même manière que les sciences médicales ont commencé à considérer la chimie au 19e siècle.

Les algorithmes constituent un vaste domaine de recherche, une branche des mathématiques, et nous n’effleurerons aujourd’hui que la surface de ce domaine. En particulier, ce domaine a accumulé résultat impressionnant sur résultat impressionnant pendant des décennies. Il peut s’agir d’un domaine de recherche assez théorique, mais cela ne signifie pas que ce n’est que de la théorie. En réalité, c’est un domaine de recherche plutôt théorique, mais il a vu émerger une multitude de découvertes qui ont trouvé leur place en production.
En fait, tout type de smartphone ou d’ordinateur que vous utilisez aujourd’hui utilise littéralement des dizaines de milliers d’algorithmes qui ont été initialement publiés quelque part. Ce palmarès est en réalité bien plus impressionnant par rapport à la théorie supply chain, où la grande majorité des supply chains ne fonctionnent pas encore sur la base des résultats de la théorie supply chain. En ce qui concerne les ordinateurs modernes et les algorithmes modernes, pratiquement tout ce qui touche aux logiciels est entièrement piloté par toutes ces décennies de découvertes issues de la recherche algorithmique. Cela constitue le cœur de pratiquement chaque ordinateur que nous utilisons aujourd’hui.
Pour la conférence d’aujourd’hui, j’ai sélectionné une liste de sujets qui, à mon avis, illustrent parfaitement ce que vous devriez savoir pour aborder le sujet des algorithmes modernes. Tout d’abord, nous discuterons de la manière dont nous pouvons réellement surpasser des algorithmes supposément optimaux, en particulier pour supply chain. Ensuite, nous jetterons un rapide coup d’œil aux structures de données, suivi de recettes magiques, de compression de tenseurs, et enfin, de méta techniques.
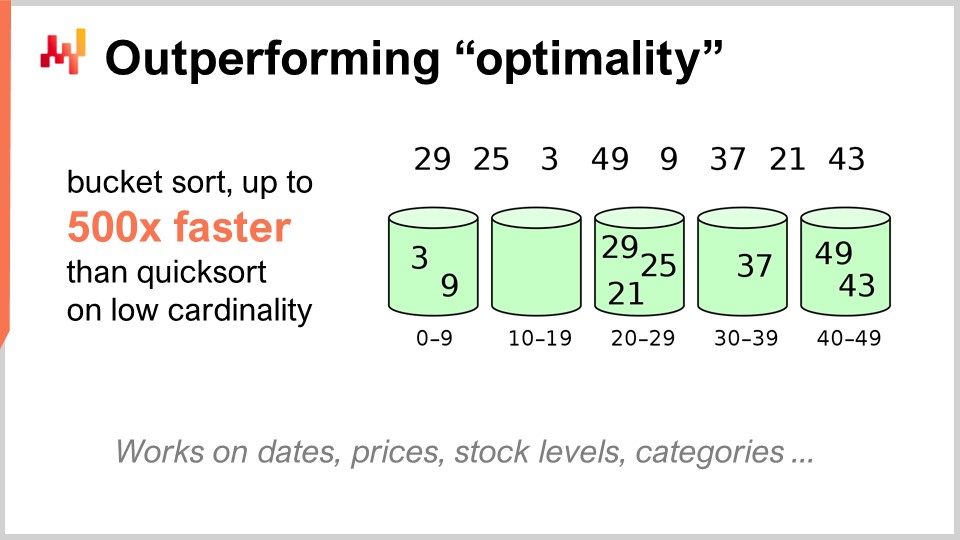
Tout d’abord, je voudrais préciser que lorsque je dis “algorithms for supply chain”, je ne fais pas référence aux algorithmes destinés à résoudre des problèmes spécifiques à la supply chain. La bonne approche consiste à examiner les algorithmes classiques pour des problèmes classiques, puis à revisiter ces problèmes sous un angle supply chain pour voir si nous pouvons réellement faire mieux. La réponse est oui, nous le pouvons.
Par exemple, l’algorithme quicksort, selon la théorie générale des algorithmes, est optimal dans le sens où il est impossible d’introduire un algorithme arbitrairement meilleur que quicksort. Dans ce contexte, quicksort est aussi bon qu’il puisse l’être. Cependant, si nous nous concentrons spécifiquement sur la supply chain, il est possible d’obtenir des accélérations stupéfiantes. En particulier, si l’on considère des problèmes de tri pour lesquels la cardinalité des ensembles de données concernés est faible, comme les dates, les prix, stock levels, ou les catégories, autant d’ensembles de données à faible cardinalité. Ainsi, si vous disposez d’hypothèses supplémentaires, telles qu’une situation de faible cardinalité, alors vous pouvez utiliser le tri par compartiments. En production, il existe de nombreuses situations où vous pouvez obtenir des accélérations absolument monumentales, jusqu’à 500 fois plus rapides que quicksort. Vous pouvez donc être des ordres de grandeur plus rapide que ce qui était supposé optimal, tout simplement parce que vous n’êtes pas dans le cas général, mais dans le cas supply chain. C’est quelque chose de très important, et je crois que c’est là toute l’essence des résultats clés impressionnants que nous pouvons obtenir en tirant parti des algorithmes pour supply chain.
Je pense que cette perspective est erronée pour au moins deux raisons. Premièrement, comme nous l’avons vu, ce n’est pas nécessairement l’algorithme standard qui nous intéresse. Nous avons constaté qu’il existe un algorithme supposément optimal, comme quicksort, mais si vous abordez le même problème sous l’angle supply chain, vous pouvez en réalité obtenir des accélérations massives. Il est donc primordial de bien connaître les algorithmes, ne serait-ce que pour pouvoir revisiter les classiques et obtenir des accélérations massives, simplement parce que vous n’êtes pas dans le cas général, mais dans le cas supply chain.
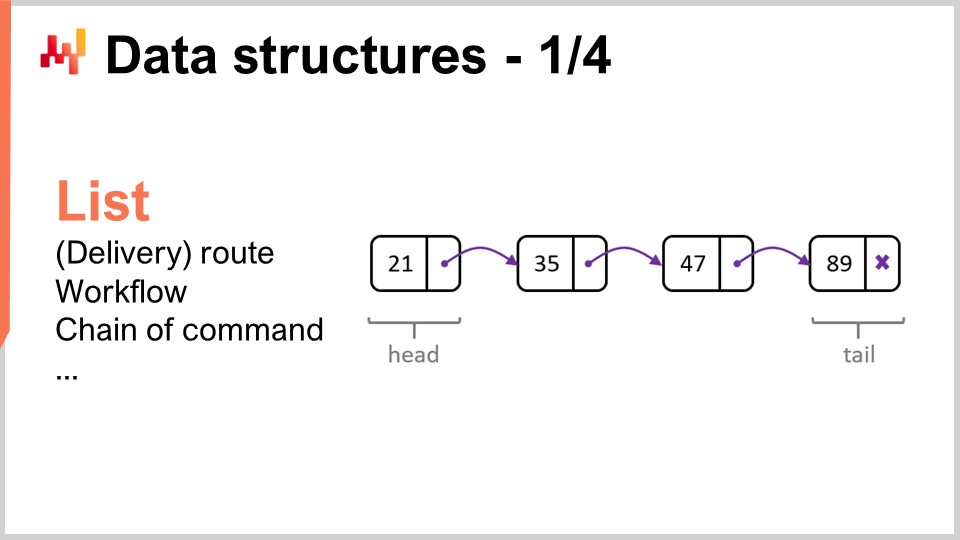
La deuxième raison pour laquelle je pense que cette perspective est erronée est que les algorithmes reposent énormément sur les structures de données. Les structures de données sont des moyens d’organiser l’information afin de pouvoir l’exploiter plus efficacement. Ce qui est intéressant, c’est que toutes ces structures de données forment en quelque sorte un vocabulaire, et y avoir accès est essentiel pour pouvoir décrire des situations supply chain de façon à ce qu’elles se traduisent facilement en logiciel. Si vous partez d’une description en termes simples, vous vous retrouvez généralement avec des éléments extrêmement difficiles à traduire en logiciel. Si vous attendez d’un ingénieur logiciel, qui ne connaît rien à la supply chain, qu’il réalise cette traduction pour vous, cela risque fort de mal tourner. Il est en réalité bien plus simple de connaître ce vocabulaire, afin de pouvoir utiliser directement les termes qui se traduisent aisément pour mettre en œuvre vos idées sous forme de logiciel.
Passons en revue les structures de données les plus populaires et les plus simples. La première serait la liste. Une liste peut être utilisée, par exemple, pour représenter un itinéraire de livraison, c’est-à-dire la séquence des livraisons à effectuer, avec une entrée par livraison. Vous pouvez énumérer l’itinéraire de livraison au fur et à mesure de son déroulement. Une liste peut également représenter un workflow, c’est-à-dire une séquence d’opérations nécessaires à la fabrication d’un certain équipement, ou une chaîne de commandement qui détermine qui est censé prendre certaines décisions.
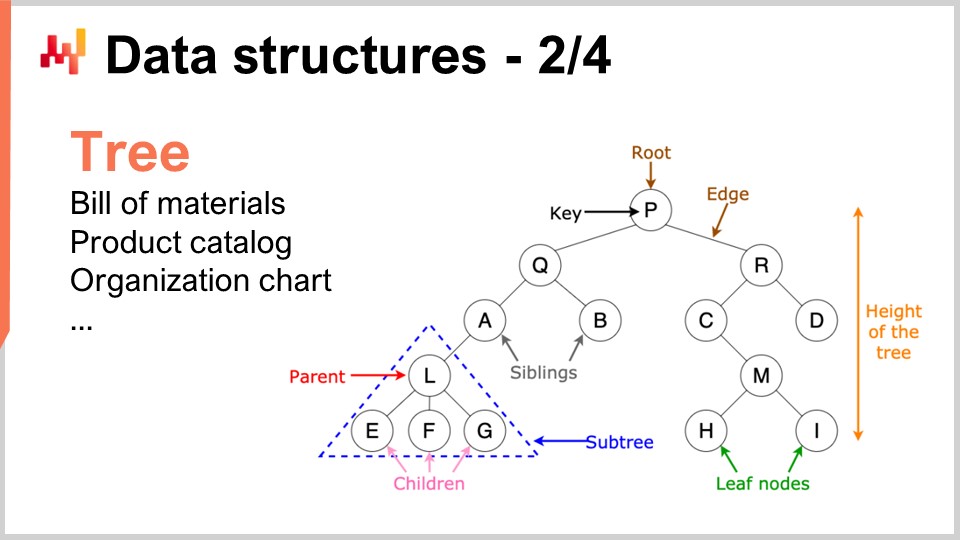
De même, les arbres sont une autre structure de données omniprésente. Au fait, les arbres algorithmiques sont à l’envers, avec la racine en haut et les branches en bas. Les arbres vous permettent de décrire toutes sortes de hiérarchies, et les supply chains possèdent des hiérarchies partout. Par exemple, une nomenclature est un arbre ; vous avez un équipement que vous souhaitez fabriquer, et cet équipement est composé d’ensembles. Chaque ensemble est constitué de sous-ensembles, et chaque sous-ensemble est composé de pièces. Si vous développez complètement la nomenclature, vous obtenez un arbre. De même, un catalogue de produits, où vous avez des familles de produits, des catégories, des produits, des sous-catégories, etc., présente très souvent une architecture de type arbre. Un organigramme, avec le PDG en haut, les cadres au niveau C en dessous, et ainsi de suite, est également représenté par un arbre. La théorie algorithmique vous fournit une multitude d’outils et de méthodes pour traiter les arbres et effectuer des opérations efficacement sur ceux-ci. Chaque fois que vous pouvez représenter des données sous forme d’arbre, vous disposez d’un véritable arsenal de méthodes mathématiques pour travailler efficacement avec ces arbres. C’est pourquoi cela revêt un grand intérêt.
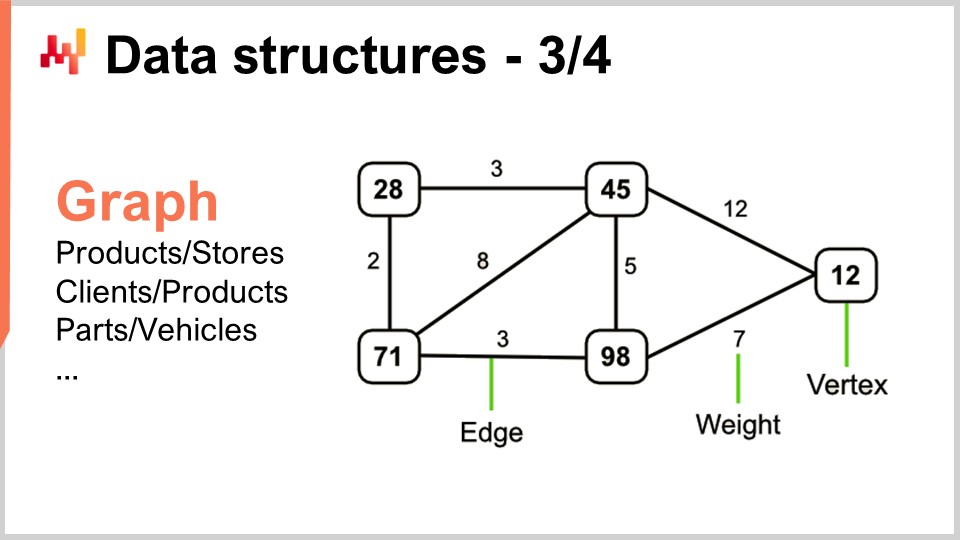
Maintenant, les graphes vous permettent de décrire toutes sortes de réseaux. Au fait, un graphe, dans le sens mathématique, est un ensemble de sommets et un ensemble d’arêtes, ces dernières reliant deux sommets entre eux. Le terme “graph” peut être un peu trompeur car il n’a rien à voir avec les graphiques. Un graphe est simplement un objet mathématique, et non un dessin ou quoi que ce soit de graphique. Une fois que vous saurez comment repérer des graphes, vous verrez que les supply chains en regorgent.
Quelques exemples : Un assortiment dans un réseau de distribution, qui est fondamentalement un graphe bipartite, relie les produits et les magasins. Si vous disposez d’un programme de fidélité dans lequel vous enregistrez quel client a acheté quel produit au fil du temps, vous obtenez un autre graphe bipartite reliant clients et produits. Dans l’après-vente automobile, où vous devez exécuter des réparations, vous devez généralement utiliser une matrice de compatibilité qui vous indique la liste des pièces ayant une compatibilité mécanique avec le véhicule concerné. Cette matrice de compatibilité est essentiellement un graphe. Il existe une quantité énorme de littérature sur toutes sortes d’algorithmes permettant de travailler avec les graphes, ce qui rend particulièrement intéressant de pouvoir caractériser un problème comme reposant sur une structure de graphe, puisque toutes les méthodes connues dans la littérature deviennent alors immédiatement disponibles.
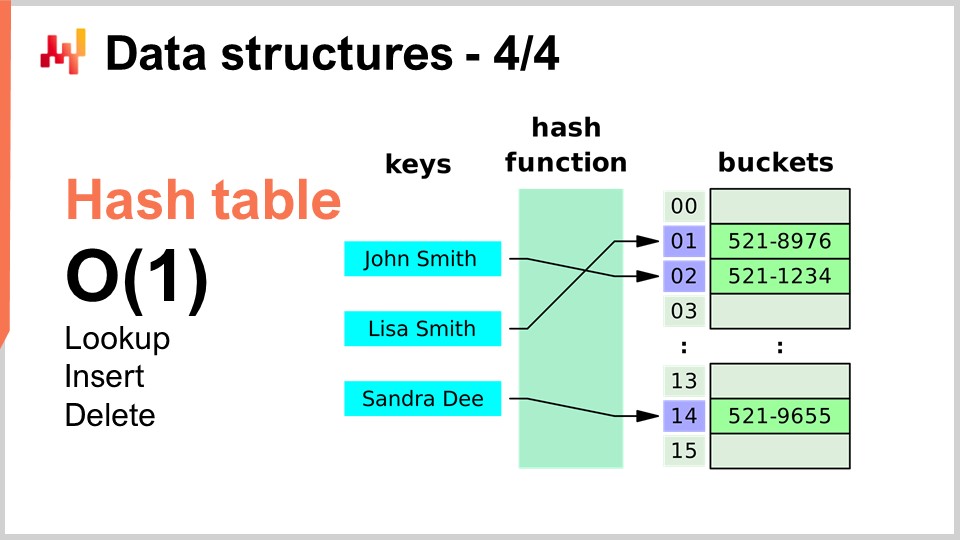
Enfin, la dernière structure de données que je vais aborder aujourd’hui est la table de hachage. La table de hachage est en quelque sorte le couteau suisse des algorithmes. Ce n’est pas nouveau ; aucune des structures de données que j’ai présentées n’est récente en soi. La table de hachage est probablement la plus récente du lot, datant des années 1950, donc elle n’est pas récente. Néanmoins, la table de hachage est une structure de données incroyablement utile. C’est un conteneur qui stocke des paires de clés et de valeurs. L’idée est qu’avec ce conteneur, vous pouvez stocker une grande quantité de données, et il vous offre des performances en O(1) pour la recherche, l’insertion et la suppression. Vous disposez d’un conteneur dans lequel vous pouvez, en temps constant, ajouter des données, vérifier si des données sont présentes (en regardant la clé) et potentiellement supprimer des données. C’est très intéressant et utile. Les tables de hachage se trouvent littéralement partout et sont largement utilisées dans d’autres algorithmes.
Une chose que je soulignerai, et que nous reverrons plus tard, est que la performance d’une table de hachage dépend fortement de la performance de la fonction de hachage que vous utilisez.

Passons maintenant aux recettes magiques, et nous allons complètement changer de perspective. Les nombres magiques sont fondamentalement un anti-pattern. Lors de la conférence précédente, celle sur la connaissance négative pour supply chain, nous avons discuté du fait que les anti-patterns commencent généralement avec une bonne intention pour finir par provoquer des conséquences inattendues qui annulent les bénéfices supposément apportés par la solution. Les nombres magiques sont un anti-pattern de programmation bien connu. Cet anti-pattern consiste à écrire du code truffé de constantes qui semblent surgir de nulle part, rendant votre logiciel très difficile à maintenir. Lorsqu’on se retrouve avec une multitude de constantes, il est difficile de comprendre pourquoi ces contraintes existent et comment elles ont été choisies.
En général, lorsque vous voyez des nombres magiques dans un programme, il vaut mieux isoler toutes ces constantes dans un endroit où elles sont plus faciles à gérer. Cependant, il existe des situations où un choix judicieux de constantes fait quelque chose de complètement inattendu, et vous obtenez des avantages quasi-magiques, totalement imprévus, en utilisant des nombres qui semblent être tombés du ciel. C’est précisément de cela qu’il s’agit dans le très court algorithme que je présente ici.
Dans la supply chain, très fréquemment, nous souhaitons pouvoir réaliser une sorte de simulation. Les simulations ou processus de Monte Carlo sont l’un des leviers de base que vous pouvez utiliser dans une myriade de situations supply chain. Cependant, la performance de votre simulation dépend énormément de votre capacité à générer des nombres aléatoires. Pour générer des simulations, il faut généralement un certain degré d’aléa, et donc, vous avez besoin d’un algorithme pour produire ce hasard. Du point de vue des ordinateurs, il s’agit typiquement de pseudohasard – ce n’est pas du vrai hasard, c’est simplement quelque chose qui ressemble à des nombres aléatoires et possède les attributs statistiques des nombres aléatoires, sans pour autant être réellement aléatoire.
La question se pose alors : avec quelle efficacité pouvez-vous générer des nombres aléatoires ? Il se trouve qu’il existe un algorithme appelé “Shift”, publié en 2003 par George Marsaglia, qui est particulièrement impressionnant. Cet algorithme génère des nombres aléatoires de très haute qualité, créant une permutation complète de 2 à la puissance 64 moins 1 bits. Il va parcourir toutes les combinaisons 64 bits, moins une, en considérant zéro comme point fixe. Il réalise cela essentiellement en six opérations : trois décalages binaires et trois opérations XOR (ou exclusif), qui sont des opérations au niveau des bits. Les décalages sont eux aussi des opérations sur les bits.
Ce que nous voyons, c’est qu’il y a trois nombres magiques au cœur de tout cela : 13, 7 et 17. Soit dit en passant, tous ces nombres sont des nombres premiers ; ce n’est pas un hasard. Il se trouve que si vous choisissez ces constantes très spécifiques, vous obtenez un excellent générateur de nombres aléatoires qui se révèle être super rapide. Quand je dis super rapide, j’entends que vous pouvez littéralement générer 10 mégaoctets par seconde de nombres aléatoires. C’est absolument énorme. Si nous revenons à la conférence précédente, nous pouvons voir pourquoi cet algorithme est également si efficace. Non seulement nous disposons d’un total de six instructions qui se traduisent directement par des instructions supportées nativement par le matériel informatique sous-jacent, comme le processeur, mais de plus, il n’y a aucune branche conditionnelle. Il n’y a aucun test, ce qui signifie que cet algorithme, une fois exécuté, exploitera au maximum la capacité de pipeline du processeur, puisqu’il n’y a pas de branchement. Nous pouvons littéralement exploiter au maximum la profonde capacité de pipeline que possèdent les processeurs modernes. C’est très intéressant.
La question est la suivante : pourrions-nous choisir d’autres nombres pour faire fonctionner cet algorithme ? La réponse est non. Il n’existe que quelques dizaines, voire environ une centaine, de combinaisons de nombres qui fonctionneraient réellement, et toutes les autres vous donneront un générateur de nombres de très mauvaise qualité. C’est là que réside le côté magique. Vous voyez, c’est une tendance récente dans le développement algorithmique de trouver quelque chose de complètement inattendu, où l’on découvre une constante semi-magique qui procure des avantages totalement imprévus en mélangeant des opérations binaires tout à fait inattendues. La génération de nombres aléatoires est d’une importance cruciale pour supply chain.

Mais, comme je le disais, les tables de hachage se trouvent partout, et il est également très intéressant de disposer d’une fonction de hachage générique ultra performante. Existe-t-elle ? Oui. Cela fait des décennies que des classes entières de fonctions de hachage sont disponibles, mais en 2019, un autre algorithme a été publié qui offre des performances record. C’est celui que vous pouvez voir à l’écran, “WyHash” de Wang Yi. Essentiellement, vous constatez que la structure est très similaire à celle de l’algorithme XORShift. C’est un algorithme sans branche, comme XORShift, et qui utilise également l’opération XOR. L’algorithme utilise six instructions : quatre opérations XOR et deux opérations Multiply-No-Flags.
Multiply-No-Flags est tout simplement la multiplication classique entre deux entiers 64 bits, et par conséquent, vous obtenez les 64 bits de poids fort et les 64 bits de poids faible. C’est une véritable instruction disponible dans les processeurs modernes, implémentée au niveau matériel, de sorte qu’elle compte comme une seule instruction informatique. Nous en avons deux. Encore une fois, nous avons trois nombres magiques, exprimés en notation hexadécimale. Soit dit en passant, ceux-ci sont des nombres premiers, de nouveau, complètement semi-magiques. Si vous appliquez cet algorithme, vous obtenez une fonction de hachage non cryptographique absolument excellente, qui fonctionne presque à la vitesse de memcpy. Elle est très rapide et revêt un intérêt primordial.

Maintenant, passons à quelque chose de complètement différent. Le succès du deep learning et de bien d’autres méthodes modernes d’apprentissage automatique repose sur quelques idées algorithmiques clés sur des problèmes qui peuvent être massivement accélérés grâce à du matériel de calcul dédié. C’est ce dont j’ai parlé dans mon cours précédent lorsque j’évoquais les processeurs comportant des instructions super-scalaires et, pour en savoir plus, les GPUs et même les TPUs. Revisitions cette idée pour voir comment tout cela a émergé de manière plutôt chaotique. Cependant, je crois que les idées pertinentes se sont cristallisées ces dernières années. Pour comprendre où nous en sommes aujourd’hui, nous devons revenir à la notation d’Einstein, qui fut introduite il y a un peu plus d’un siècle par Albert Einstein dans l’un de ses articles. L’intuition est simple : vous avez une expression y qui est une somme, pour i allant de 1 à 3, de c_y multiplié par x_y. Nous avons des expressions écrites de cette manière, et l’intuition de la notation d’Einstein consiste à dire que, dans ce genre de situation, nous devrions l’écrire en omettant entièrement la sommation. En termes de programmation, la sommation correspondrait à une boucle for. L’idée est de l’omettre complètement et d’affirmer que, par convention, nous effectuons la somme sur tous les indices de la variable i qui ont du sens.
Cette intuition simple apporte deux résultats très surprenants mais positifs. Le premier est la correction par conception. Lorsque nous écrivons explicitement la somme, nous prenons le risque de ne pas utiliser les bons indices, ce qui peut entraîner des erreurs d’indice hors limites dans le logiciel. En supprimant la sommation explicite et en affirmant que, par définition, nous utiliserons toutes les positions d’indice valides, nous obtenons une approche correcte par conception. Cela à lui seul est d’un intérêt primordial et est lié à la programmation par tableaux, un paradigme de programmation que j’ai brièvement évoqué dans l’un de mes cours précédents.
La deuxième idée, qui est plus récente et d’un grand intérêt de nos jours, est que si vous pouvez formuler votre problème sous une forme où la notation d’Einstein s’applique, votre problème peut bénéficier, en pratique, d’une accélération matérielle massive. C’est un élément révolutionnaire.

Pour comprendre pourquoi, il existe un article très intéressant intitulé “Tensor Comprehensions” publié en 2018 par l’équipe de recherche de Facebook. Ils y ont introduit la notion de tensor comprehensions. Tout d’abord, laissez-moi définir ces deux mots. Dans le domaine de l’informatique, un tenseur est essentiellement une matrice multidimensionnelle (en physique, les tenseurs sont complètement différents). Une valeur scalaire est un tenseur de dimension zéro, un vecteur est un tenseur de dimension un, une matrice est un tenseur de dimension deux, et l’on peut avoir des tenseurs avec des dimensions encore supérieures. Les tenseurs sont des objets auxquels sont attachées des propriétés similaires à celles des tableaux.
La comprehension est quelque chose d’un peu similaire à une algèbre regroupant les quatre opérations de base – addition, soustraction, multiplication et division – ainsi que d’autres opérations. Elle est plus étendue que l’algèbre arithmétique classique ; c’est pourquoi ils ont choisi d’utiliser une tensor comprehension plutôt qu’une tensor algebra. Elle est plus exhaustive, mais pas aussi expressive qu’un véritable langage de programmation complet. Lorsqu’on dispose d’une comprehension, elle est plus restrictive qu’un langage de programmation complet où l’on pourrait faire tout ce que l’on veut.
Le principe est que si vous regardez la fonction MV (def MV), c’est fondamentalement une fonction, et MV signifie matrix-vector. Dans ce cas, il s’agit d’une multiplication matrix-vector, et cette fonction effectue essentiellement une multiplication entre la matrice A et le vecteur X. Nous voyons dans cette définition que la notation d’Einstein est utilisée : nous écrivons C_i = A_ik * X_k. Quelles valeurs devons-nous choisir pour i et k ? La réponse est : toutes les combinaisons valides pour ces variables qui servent d’indices. Nous prenons toutes les valeurs d’indices valides, effectuons la somme, et en pratique, cela nous donne une multiplication matrix-vector.
En bas de l’écran, vous pouvez voir la même méthode MV réécrite avec des boucles for, en spécifiant explicitement les plages de valeurs. La réalisation clé de l’équipe de recherche de Facebook est que, chaque fois que vous pouvez écrire un programme avec cette syntaxe de tensor comprehension, ils ont développé un compilateur qui vous permet de bénéficier d’une accélération matérielle poussée grâce aux GPUs. Essentiellement, ils vous permettent d’accélérer n’importe quel programme que vous pouvez écrire avec cette syntaxe de tensor comprehension. Chaque fois que vous pouvez rédiger un programme sous cette forme, vous bénéficierez d’une accélération matérielle massive, et nous parlons ici de quelque chose qui sera deux ordres de grandeur plus rapide qu’un processeur classique. C’est un résultat stupéfiant en soi.

Voyons maintenant ce que nous pouvons faire d’un point de vue supply chain avec cette approche. Un intérêt clé pour la pratique moderne de la supply chain est le probabilistic forecasting. Le probabilistic forecasting, dont j’ai parlé dans un cours précédent, repose sur l’idée que vous n’obtiendrez pas une prévision ponctuelle, mais plutôt que vous anticiperez toutes les différentes probabilités pour une variable d’intérêt. Prenons, par exemple, une prévision de lead time. Vous souhaitez prévoir votre lead time et obtenir une prévision probabiliste de ce lead time.
Supposons maintenant que votre lead time puisse être décomposé en lead time de fabrication et lead time de transport. En réalité, vous disposez très probablement d’une prévision probabiliste pour le lead time de fabrication, qui sera une variable aléatoire discrète vous indiquant la probabilité d’observer un délai d’un jour, deux jours, trois jours, quatre jours, etc. Vous pouvez l’envisager comme un grand histogramme qui vous indique les probabilités d’observer cette durée pour le lead time de fabrication. Ensuite, vous aurez un processus similaire pour le lead time de transport, avec une autre variable aléatoire discrète fournissant une prévision probabiliste.
Maintenant, vous souhaitez calculer le lead time total. Si les lead times prévus étaient des nombres, vous feriez simplement une addition. Cependant, ces deux lead times prévus ne sont pas des nombres ; ce sont des distributions de probabilité. Ainsi, nous devons combiner ces deux distributions pour obtenir une troisième distribution, qui est celle du lead time total. Il s’avère que si nous faisons l’hypothèse que les deux lead times – le lead time de fabrication et celui de transport – sont indépendants, l’opération que nous pouvons réaliser pour sommer ces variables aléatoires n’est autre qu’une convolution unidimensionnelle. Cela peut paraître complexe, mais ce n’est en réalité pas si compliqué. Ce que j’ai implémenté, et ce que vous pouvez voir à l’écran, est l’implémentation d’une convolution unidimensionnelle entre un vecteur représentant l’histogramme des probabilités du lead time de fabrication (A) et l’histogramme associé aux probabilités du lead time de transport (B). Le résultat est le temps total, qui est la somme de ces lead times probabilistes. Si vous utilisez la notation de tensor comprehension, cela peut s’exprimer en un algorithme très compact, sur une seule ligne.
Maintenant, si nous revenons à la notation Big O que j’ai introduite plus tôt dans ce cours, nous voyons que nous avons fondamentalement un algorithme quadratique. C’est du Big O de N^2, avec N représentant la taille caractéristique des tableaux pour A et B. Comme je l’ai mentionné, des performances quadratiques constituent un point sensible dans les problèmes de prévision. Alors, que pouvons-nous faire pour remédier à ce problème ? D’abord, nous devons considérer qu’il s’agit d’un problème supply chain, et nous pouvons utiliser à notre avantage la loi des petits nombres. Comme nous l’avons évoqué dans le cours précédent, les supply chains concernent principalement de petits nombres. Si nous examinons les lead times, nous pouvons raisonnablement supposer que ces lead times seront inférieurs, disons, à 400 jours. Ce qui représente déjà une période assez longue pour cet histogramme de probabilité.
Il nous reste donc un Big O de N^2, mais avec N inférieur à 400. 400 peut être assez grand, car 400 multiplié par 400 fait 160 000. C’est un nombre significatif, et n’oubliez pas que l’addition dans cette distribution de probabilité est une opération très basique. Dès que nous commençons à faire du probabilistic forecasting, nous voudrons combiner nos prévisions de diverses manières, et il est fort probable que nous réalisions des millions de ces convolutions, car fondamentalement, ces convolutions ne sont rien d’autre qu’une addition glorifiée dans le domaine des variables aléatoires. Ainsi, même si nous avons contraint N à être inférieur à 400, il est d’un grand intérêt d’intégrer l’accélération matérielle, et c’est précisément ce que nous pouvons obtenir avec le tensor comprehension.
Le point clé à retenir est que dès que vous pouvez écrire cet algorithme, vous devez exploiter vos connaissances des concepts de supply chain pour clarifier les hypothèses applicables, puis utiliser les outils dont vous disposez pour obtenir une accélération matérielle.

Discutons maintenant des meta techniques. Les meta techniques suscitent un grand intérêt car elles peuvent être superposées aux algorithmes existants et, ainsi, si vous disposez d’un algorithme, il y a une chance que vous puissiez utiliser l’une de ces meta techniques pour améliorer ses performances. La première idée clé est la compression, tout simplement parce que des données plus légères signifient un traitement plus rapide. Comme nous l’avons vu dans le cours précédent, nous n’avons pas un accès mémoire uniforme. Si vous souhaitez accéder à davantage de données, vous devez avoir recours à différents types de mémoire physique, et à mesure que la mémoire augmente, vous vous retrouvez avec des types de mémoire beaucoup moins performants. Le cache L1 à l’intérieur du processeur est très petit, environ 64 kilo-octets, mais il est très rapide. La RAM, ou mémoire principale, est plusieurs centaines de fois plus lente que ce petit cache, mais vous pouvez en avoir littéralement un téraoctet. Il est donc essentiel de veiller à ce que vos données soient aussi compactes que possible, car cela permettra presque inévitablement d’accélérer vos algorithmes. Il existe une série d’astuces à cet égard.
Tout d’abord, vous pouvez nettoyer et organiser vos données. Cela relève du domaine des logiciels d’entreprise. Lorsque vous avez un algorithme qui s’exécute sur des données, il y a souvent beaucoup de données inutilisées qui ne contribuent pas à la solution recherchée. Il est essentiel de s’assurer que les données d’intérêt ne se retrouvent pas mêlées à celles que l’on ignore.
La deuxième idée est le bit packing. Il existe de nombreuses situations où vous pouvez intégrer certains indicateurs à l’intérieur d’autres éléments, comme des pointeurs. Vous pouvez disposer d’un pointeur 64 bits, mais il est très rare que vous ayez réellement besoin de toute l’étendue d’une adresse sur 64 bits. Vous pouvez sacrifier quelques bits de votre pointeur pour y insérer quelques indicateurs, ce qui vous permet de réduire la taille de vos données avec presque aucune perte de performance.
De plus, vous pouvez ajuster votre précision. Avez-vous vraiment besoin de 64 bits de précision en virgule flottante dans la supply chain ? Il est très rare que vous ayez effectivement besoin de cette précision. Habituellement, 32 bits de précision suffisent, et il existe même de nombreuses situations où 16 bits sont suffisants. Vous pourriez penser que réduire la précision n’est pas significatif, mais souvent, lorsque vous pouvez diviser la taille des données par un facteur de deux, vous n’accélérez pas simplement votre algorithme d’un facteur 2 ; vous l’accélérez littéralement d’un facteur 10. Le packing des données procure des bénéfices complètement non linéaires en termes de rapidité d’exécution.
Enfin, il y a le codage par entropie, qui est essentiellement une forme de compression. Cependant, vous ne souhaitez pas nécessairement utiliser des algorithmes offrant une efficacité de compression comparable, par exemple, à celle de l’algorithme utilisé pour une archive ZIP. Vous recherchez quelque chose d’un peu moins performant en termes de compression mais beaucoup plus rapide en exécution.
La compression repose fondamentalement sur l’idée que vous pouvez échanger un peu d’utilisation supplémentaire du CPU afin de réduire la pression sur la mémoire, et dans presque toutes les situations, c’est l’astuce qui importe.
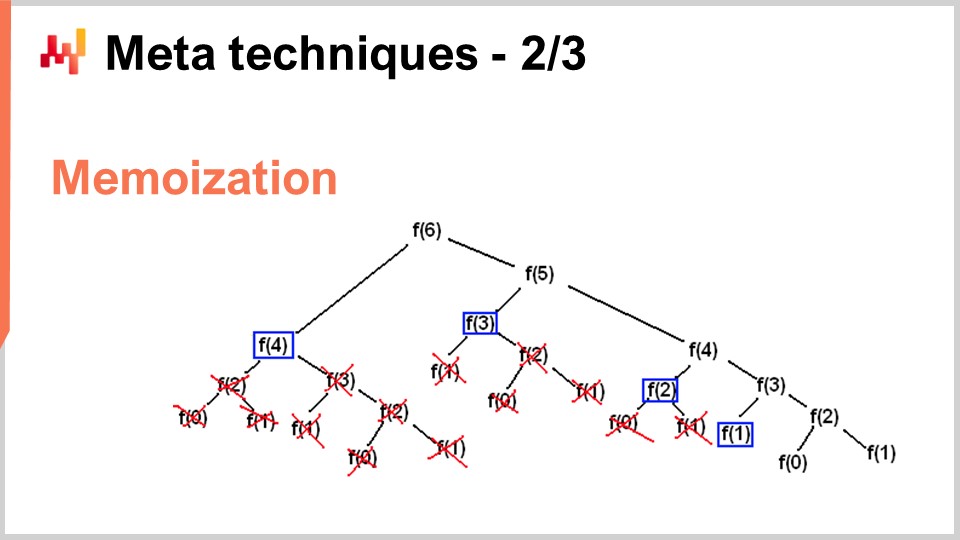
Cependant, il existe des situations où vous souhaitez faire exactement le contraire – échanger de la mémoire pour réduire considérablement votre consommation de CPU. C’est précisément ce que vous faites avec l’astuce de la mémoïsation. La mémoïsation repose sur l’idée fondamentale que si une fonction est appelée de nombreuses fois durant l’exécution de votre solution et que cette même fonction est appelée avec exactement les mêmes paramètres, il n’est pas nécessaire de la recalculer. Vous pouvez enregistrer le résultat, le mettre de côté (par exemple, dans une table de hachage), et lorsque vous appelez à nouveau la même fonction, vous pourrez vérifier si la table de hachage contient déjà une clé associée aux entrées ou si elle contient déjà le résultat parce qu’il a été pré-calculé. Si la fonction que vous mémorisez est très coûteuse, vous pouvez obtenir une accélération massive. Ce qui devient particulièrement intéressant, c’est lorsque vous commencez à utiliser la mémoïsation non pas avec la mémoire principale – comme nous l’avons vu dans le cours précédent, la DRAM est très chère –, mais lorsque vous commencez à stocker vos résultats sur disque ou sur SSD, qui sont peu coûteux et abondants. L’idée est que vous pouvez utiliser des SSD en échange d’une réduction de la charge sur le CPU, ce qui est, en quelque sorte, exactement l’inverse de la compression que je viens de décrire.
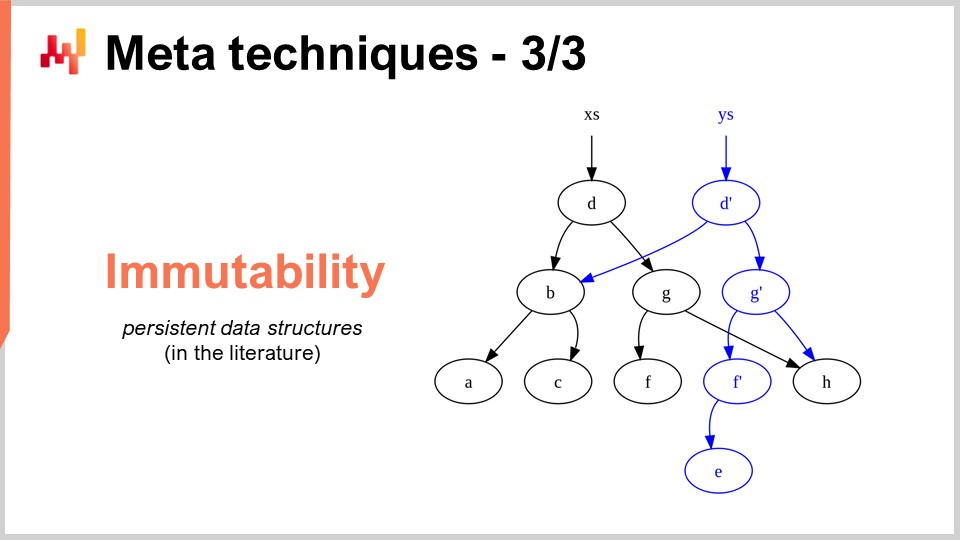
La dernière meta-technique est l’immutabilité. Les structures de données immuables sont fondamentalement des structures qui ne sont jamais modifiées. L’idée est que les changements s’ajoutent par couches. Par exemple, avec une table de hachage immutable, lorsque vous ajoutez un élément, ce que vous renvoyez est une nouvelle table de hachage qui contient tout ce qui était dans l’ancienne table plus le nouvel élément. La manière naïve de procéder serait de copier intégralement la structure de données et de renvoyer la copie complète ; cependant, cela est très inefficace. L’astuce avec les structures de données immuables est que, lorsque vous modifiez la structure, vous renvoyez une nouvelle structure qui implémente uniquement la modification, tout en réutilisant toutes les parties de l’ancienne structure qui n’ont pas été touchées.
Presque toutes les structures de données classiques, telles que les listes, les arbres, les graphes et les tables de hachage, ont leurs homologues immuables. Dans de nombreuses situations, il est très intéressant de les utiliser. D’ailleurs, il existe des langages de programmation modernes qui ont fait le choix complet de l’immutabilité, comme Clojure, par exemple, pour ceux d’entre vous qui connaissent ce langage.
Pourquoi est-ce d’un grand intérêt ? D’abord, parce que cela simplifie massivement la parallélisation des algorithmes. Comme nous l’avons vu dans le cours précédent, il n’est pas possible de trouver un processeur fonctionnant à 100 GHz pour les processeurs d’ordinateurs de bureau généraux. Ce que l’on trouve cependant, c’est une machine avec 50 cœurs, chaque cœur fonctionnant à 2 GHz. Si vous voulez tirer parti de ces nombreux cœurs, vous devez paralléliser votre exécution, ce qui expose alors votre parallélisation à de très désagréables bugs appelés conditions de course. Il devient très difficile de comprendre si l’algorithme que vous avez écrit est correct ou non, car vous pourriez avoir plusieurs processeurs qui, en même temps, essaient d’écrire sur la même zone mémoire de l’ordinateur.
Cependant, si vous avez des structures de données immuables, cela n’arrive jamais par conception, simplement parce qu’une fois qu’une structure de données est créée, elle ne changera jamais — seule une nouvelle structure de données apparaîtra. Ainsi, vous pouvez obtenir une accélération massive des performances grâce à la voie immuable, tout simplement parce que vous pouvez implémenter plus facilement des versions parallèles de vos algorithmes. Gardez à l’esprit que, généralement, le goulot d’étranglement dans l’implémentation d’une accélération algorithmique est le temps nécessaire à l’implémentation des algorithmes eux-mêmes. Si vous disposez de quelque chose qui, par conception, vous permet d’appliquer un principe de concurrence sans crainte, vous pouvez déployer des accélérations algorithmiques beaucoup plus rapidement, avec moins de ressources en termes de nombre de programmeurs impliqués. Un autre avantage important des structures de données immuables est qu’elles facilitent grandement le débogage. Lorsque vous modifiez de manière destructive une structure de données et que vous rencontrez un bug, il peut être très difficile de comprendre comment vous en êtes arrivé là. Avec un débogueur, il peut être particulièrement pénible de localiser le problème. L’aspect intéressant des structures de données immuables est que les modifications ne sont pas destructives, ce qui vous permet de voir la version précédente de votre structure de données et de mieux comprendre comment vous êtes arrivé au point où vous observez un comportement incorrect.

Pour conclure, de meilleurs algorithmes peuvent donner l’impression de super-pouvoirs. Avec de meilleurs algorithmes, vous tirez davantage parti du même matériel informatique, et ces bénéfices sont indéfinis. C’est un effort ponctuel, et ensuite vous bénéficiez d’un avantage indéfini parce que vous avez accès à des capacités de calcul supérieures, en considérant la même quantité de ressources informatiques dédiées à un problème de supply chain donné. Je crois que cette perspective offre des opportunités d’améliorations massives dans la gestion de la supply chain.
Si nous regardons un domaine complètement différent, comme les jeux vidéo, ils ont établi leurs propres traditions et découvertes algorithmiques dédiées à l’expérience de jeu. Les graphismes époustouflants que vous découvrez avec les jeux vidéo modernes sont le produit d’une communauté qui a passé des décennies à repenser l’ensemble de la pile algorithmique pour maximiser la qualité de l’expérience de jeu. La perspective dans le gaming n’est pas d’avoir un modèle 3D correct d’un point de vue physique ou scientifique, mais de maximiser la qualité perçue en termes d’expérience graphique pour le joueur, et ils ont affiné des algorithmes pour obtenir des résultats stupéfiants.
Je crois que ce type de travail n’en est qu’à ses débuts pour les supply chains. Les logiciels d’entreprise de supply chain sont bloqués et, de mon point de vue, nous n’exploitons même pas 1 % de ce que le matériel informatique moderne peut faire pour nous. La plupart des opportunités se trouvent à l’avenir et peuvent être saisies grâce aux algorithmes, non seulement les algorithmes de supply chain comme les algorithmes de routage de véhicules, mais également en revisitant les algorithmes classiques d’une perspective supply chain pour obtenir des accélérations massives en cours de route.

Maintenant, je vais regarder les questions.
Question: Vous avez parlé des spécificités de la supply chain, comme les petits nombres. Lorsque nous savons à l’avance que nous avons de petits nombres dans nos décisions potentielles, quelle simplification cela entraîne-t-il ? Par exemple, lorsque nous savons que nous pouvons commander un ou deux containers au maximum, pouvez-vous donner des exemples concrets de la manière dont cela influencerait le niveau de granularité des prévisions holistiques qui seront utilisées pour calculer la fonction de récompense des stocks ?
Tout d’abord, tout ce que j’ai présenté aujourd’hui est en production chez Lokad. Toutes ces idées, d’une manière ou d’une autre, sont très applicables à la supply chain parce qu’elles sont en production chez Lokad. Vous devez réaliser que ce que vous obtenez avec les logiciels modernes n’est pas optimisé pour tirer le meilleur parti du matériel informatique. Pensez simplement qu’ainsi que je l’ai présenté dans mon dernier cours, nous disposons aujourd’hui d’ordinateurs mille fois plus performants que ceux que nous avions il y a quelques décennies. Fonctionnent-ils mille fois plus vite ? Non. Peuvent-ils résoudre des problèmes fabuleusement plus complexes que ceux d’il y a quelques décennies ? Non. Ne sous-estimez donc pas le fait qu’il existe d’énormes potentiels d’amélioration.
Le tri par seaux que j’ai présenté dans ce cours est un exemple simple. Vous avez des opérations de tri partout dans la supply chain, et à ma connaissance, il est très rare qu’un logiciel d’entreprise profite d’algorithmes spécialisés qui correspondent parfaitement aux situations de la supply chain. Maintenant, lorsque nous savons que nous avons un ou deux containers, en tirons-nous parti chez Lokad ? Oui, nous le faisons tout le temps, et il existe une multitude d’astuces pouvant être mises en œuvre à ce niveau.
Les astuces se situent généralement à un niveau inférieur, et les bénéfices se répercuteront sur l’ensemble de la solution. Il faut penser à décomposer les problèmes de remplissage de containers en toutes leurs sous-parties. Vous pouvez tirer profit de l’application des idées et des astuces que j’ai présentées aujourd’hui à un niveau inférieur.
Par exemple, quelle précision numérique est nécessaire si nous parlons de containers ? Peut-être que des nombres sur 16 bits avec seulement 16 bits de précision pourraient suffire. Cela rend les données plus petites. Combien de produits distincts commandons-nous ? Peut-être que nous ne commandons que quelques milliers de produits distincts, ce qui nous permet d’utiliser le tri par seaux. La distribution de probabilité est à un niveau inférieur, plus restreint, donc en théorie, nous avons des histogrammes qui peuvent aller de zéro unité, à une unité, trois unités, jusqu’à l’infini, mais allons-nous jusqu’à l’infini ? Non, nous ne le faisons pas. Peut-être pouvons-nous faire des hypothèses intelligentes sur le fait qu’il est très rare de rencontrer un histogramme dépassant 1 000 unités. Dans ce cas, nous pouvons faire des approximations. Nous n’avons pas forcément besoin d’une précision de 2 unités si nous traitons un container contenant 1 000 unités. Nous pouvons faire des approximations et utiliser un histogramme avec des seaux plus grands, et ce genre de choses. Ce n’est pas tant, je dirais, l’introduction de principes algorithmiques comme la compréhension de tenseurs, qui sont incroyables parce qu’ils simplifient tout de manière très élégante. Cependant, la plupart des accélérations algorithmiques se traduisent finalement par un algorithme plus rapide mais légèrement plus compliqué. Ce n’est pas nécessairement plus simple, car généralement, l’algorithme le plus simple est aussi un peu inefficace. Un algorithme plus approprié pour un cas donné peut être un peu plus long à écrire et plus complexe, mais au final, il s’exécutera plus rapidement. Ce n’est pas toujours le cas, comme nous l’avons vu avec les recettes magiques, mais ce que je voulais montrer, c’est que nous devons revisiter les éléments de base fondamentaux de ce que nous faisons pour réellement construire des logiciels d’entreprise.
Question: Dans quelle mesure ces idées sont-elles mises en œuvre chez les fournisseurs dERP, les systèmes APS, et les best of breeds comme GTA ?
Le point intéressant est que ces idées sont, fondamentalement, pour la plupart, complètement incompatibles avec les logiciels transactionnels. La plupart des logiciels d’entreprise sont construits autour d’un noyau qui est une base de données transactionnelle, et tout est canalisé par cette base de données. Cette dernière n’est pas spécifique à la supply chain ; c’est une base de données générique censée être capable de gérer toutes les situations possibles auxquelles vous pouvez penser, de la finance à l’informatique scientifique, en passant par les dossiers médicaux, et plus encore.
Le problème est que si le logiciel que vous examinez a une base de données transactionnelle à son cœur, alors les idées que j’ai proposées ne peuvent pas être mises en œuvre par conception. C’est un peu la fin du jeu. Si vous regardez les jeux vidéo, combien de jeux vidéo sont construits au-dessus d’une base de données transactionnelle ? La réponse est zéro. Pourquoi ? Parce que vous ne pouvez pas obtenir de bonnes performances graphiques en vous appuyant sur une base de données transactionnelle. Vous ne pouvez pas réaliser des graphismes informatiques dans une base de données transactionnelle.
Une base de données transactionnelle est très appréciable ; elle offre la transactionnalité, mais elle vous enferme dans un univers où presque toutes les accélérations algorithmiques auxquelles vous pourriez penser ne peuvent tout simplement pas s’appliquer. Je crois que lorsque nous commençons à penser aux APS, il n’y a rien d’avancé dans ces systèmes. Ils sont bloqués dans le passé depuis des décennies, et ce blocage est dû au fait qu’au cœur de leur conception, ils reposent entièrement sur une base de données transactionnelle qui les empêche d’appliquer les idées apparues dans le domaine des algorithmes au cours des quatre dernières décennies.
Voilà l’essence même du problème dans le domaine des logiciels d’entreprise. Les décisions de conception que vous prenez dès le premier mois de la conception de votre produit vous hanteront pendant des décennies, essentiellement jusqu’à la fin des temps. Vous ne pouvez pas améliorer votre produit une fois que vous avez opté pour une conception spécifique ; vous y êtes condamné. Tout comme vous ne pouvez pas simplement reconfigurer une voiture pour qu’elle devienne électrique, si vous voulez une très bonne voiture électrique, vous devez repenser entièrement la voiture autour de l’idée que le moteur de propulsion sera électrique. Il ne s’agit pas simplement de changer le moteur et de dire, “Voici une voiture électrique.” Ça ne fonctionne pas comme cela. C’est l’un de ces principes de conception fondamentaux où, une fois que vous vous êtes engagé à produire une voiture électrique, vous devez repenser tout ce qui entoure le moteur pour que ce soit adéquat. Malheureusement, les ERP et APS, qui sont très centrés sur la base de données, ne peuvent tout simplement pas utiliser ces idées, j’en ai bien peur. Il est toujours possible d’avoir une bulle isolée où vous bénéficiez de ces astuces, mais ce sera un add-on rajouté ; cela n’atteindra jamais le cœur du système.
En ce qui concerne les capacités impressionnantes de Blue Yonder, merci de faire preuve de compréhension, car Lokad est un concurrent direct de Blue Yonder, et il m’est difficile de rester complètement impartial. Sur le marché des logiciels d’entreprise, il faut formuler des affirmations ridiculement audacieuses pour rester compétitif. Je ne suis pas convaincu qu’il y ait une quelconque substance dans ces affirmations. Je remets en question l’idée que quiconque sur ce marché possède quelque chose qui pourrait être qualifié d’impressionnant.
Si vous voulez voir quelque chose d’époustouflant et d’ultra-impressionnant, regardez la dernière démo de l’Unreal Engine ou des algorithmes spécialisés pour les jeux vidéo. Considérez les graphismes sur le matériel de prochaine génération de la PlayStation 5 ; ils sont absolument stupéfiants. Avons-nous quelque chose dans le même ordre de prouesses technologiques dans le domaine des logiciels d’entreprise ? En ce qui concerne Lokad, j’ai une opinion extrêmement biaisée, mais de manière plus générale, je vois un océan de personnes qui tentent d’exploiter au maximum les bases de données relationnelles depuis des décennies. Parfois, ils introduisent d’autres types de bases de données, comme les bases de données graphe, mais cela passe complètement à côté des idées que j’ai présentées. Cela n’apporte rien de substantiel pour offrir de la valeur au monde de la supply chain.
Le message clé ici pour le public est qu’il s’agit d’une question de conception. Nous devons nous assurer que les décisions initiales qui ont guidé la conception de votre logiciel d’entreprise ne sont pas du genre à, par conception, empêcher l’utilisation de ce type de techniques dès le départ.
Le prochain cours aura lieu dans trois semaines, mercredi à 15 h, heure de Paris. Ce sera le 13 juin, et nous reviendrons sur le troisième chapitre, qui porte sur le personnel de la supply chain, des traits de personnalité surprenants et des entreprises fictives. La prochaine fois, nous parlerons de fromage. À bientôt !


