Prévision probabilistique pour Supply Chain - Lecture 5.2

00:01 Introduction
02:18 La prévision moderne
06:37 Passer en mode postal probabilistique
11:58 L’histoire jusqu’à présent
15:10 Plan probable pour aujourd’hui
17:18 Bestiaire des prédictions
28:10 Métriques - CRPS - 1/2
33:21 Métriques - CRPS - 2/2
37:20 Métriques - Monge-Kantorovich
42:07 Métriques - vraisemblance - 1/3
47:23 Métriques - vraisemblance - 2/3
51:45 Métriques - vraisemblance - 3/3
55:03 Distributions 1D - 1/4
01:01:13 Distributions 1D - 2/4
01:06:43 Distributions 1D - 3/4
01:15:39 Distributions 1D - 4/4
01:18:24 Générateurs - 1/3
01:24:00 Générateurs - 2/3
01:29:23 Générateurs - 3/3
01:37:56 Veuillez patienter pendant que nous vous ignorons
01:40:39 Conclusion
01:43:50 Prochaine conférence et questions du public

Description

Une prévision est dite probabilistique, plutôt que déterministe, si elle contient un ensemble de probabilités associées à toutes les issues futures possibles, plutôt que de désigner une issue particulière comme “la” prévision. Les prévisions probabilistiques sont importantes chaque fois que l’incertitude est irréductible, ce qui est presque toujours le cas lorsqu’il s’agit de systèmes complexes. Pour les supply chain, les prévisions probabilistiques sont essentielles pour produire des décisions robustes face à des conditions futures incertaines.

Transcription complète

Bienvenue dans cette série de conférences sur la supply chain. Je suis Joannes Vermorel, et aujourd’hui je vais présenter « Prévision probabilistique pour Supply Chain ». La prévision probabilistique est l’un des changements de paradigme les plus importants, sinon le plus important, en plus d’un siècle de science de la prévision statistique. Pourtant, au niveau technique, il s’agit principalement de la même chose. Si nous examinons des modèles de prévision probabilistique ou leurs alternatives non probabilistiques, ce sont les mêmes statistiques, les mêmes probabilités. La prévision probabilistique reflète un changement dans notre façon de concevoir la prévision elle-même. Le plus grand changement apporté par la prévision probabilistique à la supply chain ne se trouve pas dans la science de la prévision. Le plus grand changement se trouve dans la manière dont les supply chain sont exploitées et optimisées en présence de modèles prédictifs.

L’objectif de la conférence d’aujourd’hui est de présenter une introduction technique en douceur à la prévision probabilistique. À la fin de cette conférence, vous devriez être en mesure de comprendre de quoi il s’agit, comment différencier les prévisions probabilistiques des prévisions non probabilistiques, comment évaluer la qualité d’une prévision probabilistique, et même être capable de concevoir votre propre modèle de prévision probabilistique d’entrée de gamme. Aujourd’hui, je ne traiterai pas de l’exploitation des prévisions probabilistiques à des fins de prise de décision dans le contexte des supply chain. L’accent est exclusivement mis sur l’établissement des fondations de la prévision probabilistique. L’amélioration des processus de prise de décision dans la supply chain via des prévisions probabilistiques sera abordée dans la prochaine conférence.

Pour comprendre l’importance des prévisions probabilistiques, il est nécessaire d’apporter un peu de contexte historique. La forme moderne de la prévision, la prévision statistique, par opposition à la divination, est apparue au tout début du 20e siècle. La prévision a émergé dans un contexte scientifique plus large où les sciences dures, quelques disciplines très réussies telles que la cinétique, l’électromagnétisme et la chimie, ont pu obtenir des résultats apparemment d’une précision arbitraire. Ces résultats ont été obtenus grâce à ce qui s’apparente essentiellement à un effort de plusieurs siècles, qui peut être retracé, par exemple, jusqu’à Galileo Galilei, dans le développement de technologies supérieures qui auraient permis des formes de mesure plus performantes. Des mesures plus précises, à leur tour, favoriseraient un développement scientifique ultérieur en permettant aux scientifiques de tester et de mettre à l’épreuve leurs théories et leurs prédictions de manière encore plus précise.

Dans ce contexte plus large où certaines sciences ont rencontré un succès incroyable, le domaine naissant de la prévision au début du 20e siècle s’est donné pour mission de reproduire essentiellement ce que ces sciences dures avaient accompli dans le domaine de l’économie. Par exemple, si l’on considère des pionniers tels que Roger Babson, l’un des pères de la prévision économique moderne, il a fondé une entreprise de prévision économique couronnée de succès aux États-Unis au début du 20e siècle. La devise de l’entreprise était littéralement : “For every action, there is an equal and opposite reaction.” La vision de Babson était de transposer le succès de la physique newtonienne dans le domaine de l’économie et, en fin de compte, d’obtenir des résultats tout aussi précis.

Cependant, après plus d’un siècle de prévisions académiques statistiques, dans lesquelles opèrent les supply chain, l’idée d’atteindre des résultats d’une précision arbitraire, ce qui se traduit en termes de prévision par l’obtention de prévisions arbitrairement précises, reste aussi insaisissable qu’elle ne l’était il y a plus d’un siècle. Depuis quelques décennies, des voix dans le monde plus large de la supply chain ont exprimé des préoccupations quant au fait que ces prévisions ne deviendraient jamais suffisamment précises. Un mouvement, tel que le lean manufacturing, parmi d’autres, a été un ardent défenseur de la réduction drastique de la dépendance des supply chain à l’égard de ces prévisions peu fiables. C’est ce dont parle le just-in-time : si vous pouvez fabriquer et fournir exactement ce dont le marché a besoin au moment opportun, alors tout à coup, vous n’avez plus besoin d’une prévision fiable et précise.

Dans ce contexte, la prévision probabilistique constitue une réhabilitation de la prévision, mais avec des ambitions bien plus modestes. La prévision probabilistique part de l’idée qu’il existe une incertitude irréductible quant à l’avenir. Tous les futurs sont possibles, mais ils ne le sont pas tous de manière égale, et l’objectif de la prévision probabilistique est d’évaluer de manière comparative la probabilité respective de tous ces futurs alternatifs, et non de réduire tous les futurs possibles à un seul futur.

La perspective newtonienne sur les prévisions économiques statistiques a essentiellement échoué. L’opinion au sein de notre communauté selon laquelle il serait un jour possible d’atteindre des prévisions d’une précision arbitraire a largement disparu. Pourtant, de façon étonnante, presque tous les logiciels de supply chain et une grande partie des pratiques supply chain grand public reposent en réalité sur l’hypothèse que de telles prévisions seront finalement disponibles.

Par exemple, le Sales and Operations Planning (S&OP) repose sur l’idée qu’une vision unifiée et quantifiée de l’entreprise peut être obtenue si toutes les parties prenantes se réunissent et collaborent à l’élaboration d’une prévision. De même, l’open-to-buy est également essentiellement une méthode fondée sur l’idée qu’il est possible de construire des prévisions top-down d’une précision arbitraire dans le cadre d’un processus budgétaire hiérarchique. De plus, même si l’on considère de nombreux outils très courants en matière de prévision et de planification dans le domaine des supply chain, tels que la business intelligence et les spreadsheets, ces outils sont largement conçus pour une prévision ponctuelle de séries temporelles. Essentiellement, l’idée est de pouvoir prolonger vos données historiques dans le futur, avec un point par période d’intérêt. Ces outils, par conception, présentent une énorme friction lorsqu’il s’agit même de comprendre le type de calculs impliqué dans une prévision probabilistique, où il n’y a pas un seul futur, mais tous les futurs possibles.

En effet, la prévision probabilistique ne consiste pas à orner une prévision classique d’une forme d’incertitude. La prévision probabilistique ne consiste pas non plus à établir une liste restreinte de scénarios, chaque scénario constituant une prévision classique en soi. Les méthodes supply chain grand public ne fonctionnent généralement pas avec des prévisions probabilistiques car, au fond, elles reposent implicitement ou explicitement sur l’idée qu’il existe une sorte de prévision de référence, autour de laquelle tout pivote. En revanche, la prévision probabilistique est l’évaluation numérique frontale de tous les futurs possibles.

Naturellement, nous sommes limités par la quantité de ressources informatiques dont nous disposons, ainsi lorsque je dis “tous les futurs possibles”, en pratique, nous ne considérerons qu’un nombre fini de futurs. Cependant, compte tenu de la puissance de traitement moderne dont nous disposons, le nombre de futurs que nous pouvons réellement envisager se compte en millions. C’est là que la business intelligence et les spreadsheets peinent. Ils ne sont pas conçus pour le type de calculs impliqués dans la gestion des prévisions probabilistiques. C’est un problème de conception logicielle. Vous voyez, un spreadsheet a accès aux mêmes ordinateurs et à la même puissance de traitement, mais si le logiciel n’est pas conçu de manière adéquate, certaines tâches peuvent être incroyablement difficiles à réaliser, même si vous disposez d’une immense puissance de traitement.

Ainsi, du point de vue de la supply chain, le plus grand défi pour adopter la prévision probabilistique est de renoncer à des décennies d’outils et de pratiques enracinés dans un objectif très ambitieux, mais que je crois erroné, à savoir qu’il serait possible d’obtenir des prévisions d’une précision arbitraire. Je tiens à souligner immédiatement qu’il serait extrêmement erroné de considérer la prévision probabilistique comme un moyen d’obtenir des prévisions plus précises. Ce n’est pas le cas. Les prévisions probabilistiques ne sont pas plus précises et ne peuvent pas être utilisées comme substitut direct aux prévisions classiques et grand public. La supériorité des prévisions probabilistiques réside dans les manières dont elles peuvent être exploitées pour des fins supply chain, en particulier pour la prise de décision dans le contexte des supply chain. Cependant, notre objectif aujourd’hui est simplement de comprendre de quoi traitent ces prévisions probabilistiques, et leur exploitation viendra dans la prochaine conférence.

Cette conférence fait partie d’une série de conférences sur la supply chain. J’essaie de maintenir ces conférences suffisamment indépendantes les unes des autres. Cependant, nous arrivons à un point où il sera vraiment utile pour le public que ces conférences soient visionnées en séquence, car je ferai fréquemment référence à ce qui a été présenté dans les conférences précédentes.

Ainsi, cette conférence est la troisième du cinquième chapitre, qui est dédié au predictive modeling. Dans le tout premier chapitre de cette série, j’ai présenté mes points de vue sur les supply chain en tant que domaine d’étude et en tant que pratique. Dans le deuxième chapitre, j’ai présenté les méthodologies. En effet, la plupart des situations de supply chain sont de nature conflictuelle, et ces situations tendent à faire échouer les méthodologies naïves. Nous devons disposer de méthodologies adéquates si nous voulons réussir, même modestement, dans le domaine des supply chain.

Le troisième chapitre était consacré à la parcimonie en supply chain, avec un focus exclusif sur le problème et la nature même du défi auquel nous sommes confrontés dans diverses situations couvertes par les supply chain. L’idée derrière la parcimonie en supply chain est d’ignorer complètement tous les aspects liés à la solution, car nous voulons uniquement examiner le problème avant de choisir la solution que nous souhaitons utiliser pour y répondre.

Dans le quatrième chapitre, j’ai passé en revue un large éventail de sciences auxiliaires. Ces sciences ne concernent pas la supply chain en tant que telle ; ce sont d’autres domaines de recherche qui sont adjacents ou complémentaires. Cependant, je crois qu’une maîtrise de base de ces sciences auxiliaires est indispensable pour la pratique moderne des supply chain.

Enfin, dans le cinquième chapitre, nous abordons les techniques qui nous permettent de quantifier et d’évaluer l’avenir, notamment pour formuler des affirmations à propos du futur. En effet, tout ce que nous faisons en supply chain reflète, dans une certaine mesure, une anticipation de l’avenir. Si nous pouvons anticiper l’avenir de manière plus efficace, alors nous serons capables de prendre de meilleures décisions. C’est de cela qu’il s’agit dans ce cinquième chapitre : obtenir des aperçus quantifiables et améliorés de l’avenir. Dans ce chapitre, les prévisions probabilistiques représentent une voie pivot dans notre approche pour appréhender le futur.

Le reste de cette conférence est divisé en quatre sections de longueur inégale. Tout d’abord, nous allons passer en revue les types de prévisions les plus courants, au-delà de la prévision classique. Je vais préciser ce que j’entends par prévision classique dans un instant. En effet, trop peu de personnes dans les cercles supply chain réalisent qu’il existe de nombreuses options. La prévision probabilistique doit elle-même être comprise comme une couverture englobant un ensemble assez diversifié d’outils et de techniques.

Ensuite, nous présenterons des métriques pour évaluer la qualité des prévisions probabilistiques. Quoi qu’il en soit, une prévision probabilistique bien conçue vous dira toujours, “Eh bien, il y avait une probabilité pour que cela se produise.” La question devient alors : comment distinguer une bonne prévision probabilistique d’une mauvaise ? C’est là que ces métriques entrent en jeu. Il existe des métriques spécialisées entièrement dédiées à la situation de la prévision probabilistique.

Troisièmement, nous examinerons en profondeur les distributions unidimensionnelles. Elles représentent le type de distribution le plus simple et, bien qu’elles présentent des limites évidentes, elles constituent également le point d’entrée le plus accessible dans le domaine de la prévision probabilistique.

Quatrièmement, nous aborderons brièvement les générateurs, souvent appelés méthodes Monte Carlo. En effet, il existe une dualité entre les générateurs et les estimateurs de densité de probabilité, et ces méthodes Monte Carlo nous offriront une voie pour aborder des problèmes de dimensions supérieures et des formes de prévision probabilistique.

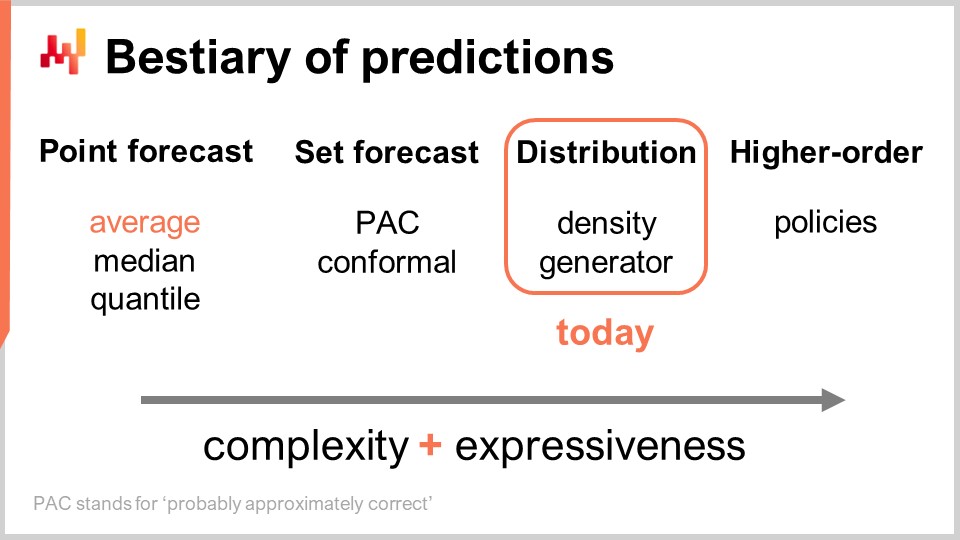
Il existe plusieurs types de prévisions, et cet aspect ne doit pas être confondu avec le fait qu’il existe plusieurs types de modèles de prévision. Lorsque les modèles n’appartiennent pas au même type ou à la même classe de prévisions, ils ne résolvent même pas les mêmes problèmes. Le type de prévision le plus courant est la prévision ponctuelle. Par exemple, si je dis que demain les ventes totales en euros dans un magasin seront de 10 000 euros pour l’agrégat des ventes totales de la journée, je fais une prévision ponctuelle de ce qui se passera dans ce magasin demain. Si je répète cet exercice et commence à construire une prévision des séries temporelles en faisant une déclaration pour le jour de demain, puis une autre déclaration pour le jour d’après demain, j’aurai plusieurs points de données. Cependant, tout cela reste une prévision ponctuelle parce qu’en essence, nous choisissons notre problème en sélectionnant un certain niveau d’agrégation et, à ce niveau, nos prévisions nous fournissent un chiffre unique censé être la réponse.

Maintenant, au sein du type de prévision ponctuelle, il existe plusieurs sous-types de prévisions selon la métrique optimisée. La métrique la plus couramment utilisée est probablement l’erreur quadratique, ainsi nous avons une erreur quadratique moyenne qui vous donne la prévision moyenne. D’ailleurs, cela tend à être la prévision la plus utilisée car c’est la seule prévision qui est au moins quelque peu additive. Aucune prévision n’est jamais entièrement additive ; elle s’accompagne toujours de nombreuses réserves. Cependant, certaines prévisions sont plus additives que d’autres, et clairement, les prévisions moyennes tendent à être les plus additives de toutes. Si vous voulez obtenir une prévision moyenne, ce que vous avez essentiellement est une prévision ponctuelle optimisée selon l’erreur quadratique moyenne. Si vous utilisez une autre métrique, comme l’erreur absolue, et l’optimisez en fonction de celle-ci, ce que vous obtiendrez sera une prévision médiane. Si vous utilisez la pinball loss function que nous avons introduite dès la toute première conférence de ce cinquième chapitre dans cette série de conférences sur la supply chain, ce que vous obtiendrez sera une quantile forecast. D’ailleurs, comme nous pouvons le constater aujourd’hui, je classe les prévisions quantiles simplement comme un autre type de prévision ponctuelle. En effet, avec une prévision quantile, vous obtenez essentiellement une seule estimation. Cette estimation peut comporter un biais, ce qui est voulu. C’est de cela qu’il s’agit avec les quantiles, mais néanmoins, à mon avis, cela qualifie bel et bien de prévision ponctuelle puisque la forme de la prévision se réduit à un seul point.

Maintenant, il existe la prévision par ensemble, qui renvoie un ensemble de points au lieu d’un seul point. Il existe une variation selon la manière dont vous construisez cet ensemble. Si nous examinons une prévision PAC — PAC signifiant Probably Approximately Correct — c’est essentiellement un cadre introduit par Valiant il y a environ deux décennies, et il stipule que l’ensemble, c’est-à-dire votre prédiction, comporte une certaine probabilité que le résultat observé se situe dans cet ensemble prédéfini. L’ensemble que vous produisez réunit en fait tous les points se trouvant dans une région caractérisée par une distance maximale à un point de référence. D’une certaine manière, la perspective PAC sur la prévision relève déjà d’une prévision par ensemble car le résultat n’est plus un point unique. Cependant, nous disposons toujours d’un point de référence, d’un résultat central, et d’une distance maximale par rapport à ce point central. Nous affirmons simplement qu’il existe une probabilité spécifiée selon laquelle le résultat sera finalement observé dans notre ensemble de prédiction.

L’approche PAC peut être généralisée par l’approche conforme. La prédiction conforme stipule : “Voici un ensemble, et je vous dis qu’il existe cette probabilité donnée que le résultat se situe dans cet ensemble.” Là où la prédiction conforme généralise l’approche PAC, c’est que les prédictions conformes ne sont plus attachées à un point de référence et à la distance par rapport à ce point. Vous pouvez modeler cet ensemble comme bon vous semble, tout en restant dans le paradigme de la prévision par ensemble.

Le futur peut être représenté de manière encore plus granulaire et complexe : la prévision de distribution. La prévision de distribution vous fournit une fonction qui associe tous les résultats possibles à leurs densités de probabilité locales respectives. D’une certaine manière, nous commençons par la prévision ponctuelle, où la prévision se limite à un point. Puis nous passons à la prévision par ensemble, où la prévision est constituée d’un ensemble de points. Enfin, la prévision de distribution est techniquement une fonction ou quelque chose qui en est une généralisation. D’ailleurs, quand j’emploie le terme “distribution” dans cette conférence, il se réfère implicitement à une distribution de probabilités. Les prévisions de distribution représentent quelque chose de bien plus riche et complexe qu’un simple ensemble, et ce sera le sujet de notre discussion aujourd’hui.

Il existe deux manières courantes d’aborder les distributions : l’approche par densité et l’approche génératrice. Lorsque je parle de “densité”, cela se réfère essentiellement à l’estimation locale des densités de probabilité. L’approche génératrice implique un processus génératif de Monte Carlo qui produit des résultats, appelés déviations, censées refléter la même densité de probabilité locale. Ce sont les deux approches principales pour traiter les prévisions de distribution.

Au-delà de la distribution, nous avons des constructions d’ordre supérieur. Cela peut être un peu compliqué à comprendre, mais mon propos ici, même si nous n’abordons pas les constructions d’ordre supérieur aujourd’hui, est simplement d’indiquer que la prévision probabiliste, lorsqu’elle se focalise sur la génération de distributions, n’est pas la finalité ; ce n’est qu’une étape, et il y a bien plus encore. Les constructions d’ordre supérieur sont importantes si nous voulons un jour obtenir des réponses satisfaisantes à des situations simples.

Pour comprendre ce que sont les constructions d’ordre supérieur, considérons un simple magasin de détail doté d’une politique de remise pour les produits approchant de leur date de péremption. Évidemment, le magasin ne souhaite pas avoir de stocks morts, de sorte qu’une remise automatique est appliquée lorsque les produits sont très proches de leur date de péremption. La demande que ce magasin générerait dépend fortement de cette politique. Ainsi, la prévision que nous souhaiterions obtenir — qui pourrait être une distribution représentant les probabilités de tous les résultats possibles — devrait être fonction de cette politique. Cependant, cette politique est un objet mathématique ; c’est une fonction. Ce que nous souhaiterions obtenir n’est pas une prévision probabiliste mais quelque chose de plus méta : une construction d’ordre supérieur qui, étant donnée une politique, peut générer la distribution résultante.

D’un point de vue supply chain, passer d’un type de prévision à un autre nous procure bien plus d’informations. Cela ne doit pas être confondu avec une meilleure précision de la prévision ; il s’agit d’accéder à un type d’information complètement différent, un peu comme passer d’une vision en noir et blanc à la capacité subite de percevoir les couleurs, au lieu de simplement obtenir une résolution supplémentaire. En termes d’outils, les tableurs et outils de business intelligence sont quelque peu adaptés à la gestion des prévisions ponctuelles. Selon le type de prévision par ensemble que vous envisagez, ils peuvent suffire, mais vous sollicitez déjà leurs capacités de conception à l’extrême. Ils ne sont pas vraiment conçus pour gérer tout type de prévision par ensemble sophistiquée, au-delà de l’évidente qui consiste simplement à définir une plage de valeurs minimales et maximales dans la zone des valeurs attendues. Nous verrons qu’essentiellement, si nous voulons espérer travailler avec des prévisions de distribution ou même des constructions d’ordre supérieur, nous aurons besoin d’un autre type d’outillage, bien que cela devienne plus clair dans un instant.

Pour démarrer avec les prévisions probabilistes, essayons de caractériser ce qui fait une bonne prévision probabiliste. En effet, quoi qu’il arrive, une prévision probabiliste vous indiquera que, quel que soit le résultat observé, il y avait une certaine probabilité pour que cela se produise. Alors, dans ces conditions, comment différencier une bonne prévision probabiliste d’une mauvaise ? Ce n’est certainement pas parce qu’elle est probabiliste que soudainement tous les modèles de prévision deviennent bons.

C’est exactement de cela qu’il est question dans les métriques dédiées à la prévision probabiliste, et le Continuous Ranked Probability Score (CRPS) est la generalization de l’erreur absolue pour les prévisions probabilistes unidimensionnelles. Je suis absolument désolé pour ce nom épouvantable – le CRPS. Je n’ai pas inventé cette terminologie ; elle m’a été transmise. La formule du CRPS est affichée à l’écran. Essentiellement, la fonction F est la fonction de distribution cumulative ; c’est la prévision probabiliste réalisée. Le point x est l’observation effective, et la valeur du CRPS est calculée en comparant votre prévision probabiliste et l’unique observation que vous venez d’effectuer.

Nous pouvons constater qu’essentiellement, le point se transforme lui-même en une prévision quasi-probabiliste via la fonction échelon de Heaviside. Introduire la fonction échelon de Heaviside revient simplement à transformer le point que nous venons d’observer en une distribution de Dirac, c’est-à-dire une distribution qui concentre toute la masse de probabilité sur un résultat unique. Ensuite, vient une intégrale, et en essence, le CRPS effectue une sorte d’appariement de formes. Nous mettons en correspondance la forme de la fonction de distribution cumulative (FDC) avec celle d’une autre FDC, celle associée au Dirac correspondant au point observé.

Du point de vue d’une prévision ponctuelle, le CRPS est déroutant non seulement à cause de sa formule compliquée, mais également parce que cette métrique prend deux arguments qui n’ont pas le même type. L’un de ces arguments est une distribution, et l’autre n’est qu’un seul point de données. Ainsi, nous faisons face à une asymétrie qui n’existe pas avec la plupart des autres métriques de prévision ponctuelle, telles que l’erreur absolue et l’erreur quadratique moyenne. Dans le CRPS, nous comparons essentiellement un point à une distribution.

Si nous voulons comprendre davantage ce que nous calculons avec le CRPS, une observation intéressante est que le CRPS possède la même unité que l’observation. Par exemple, si x est exprimé en euros, et que la valeur du CRPS entre F et x est également homogène avec l’unité euro, c’est pourquoi je dis que le CRPS est une généralisation de l’erreur absolue. D’ailleurs, si vous réduisez votre prévision probabiliste à un Dirac, le CRPS vous donne une valeur équivalente à l’erreur absolue.

Bien que le CRPS puisse paraître assez intimidant et complexe, son implémentation est en réalité raisonnablement simple. À l’écran se trouve un petit script Envision qui illustre comment le CRPS peut être utilisé d’un point de vue langagier. Envision est un langage de programmation spécifique au domaine, dédié à l’optimisation prédictive des supply chains, développé par Lokad. Dans ces conférences, j’utilise Envision par souci de clarté et de concision. Toutefois, notez bien qu’il n’y a rien d’unique à Envision ; les mêmes résultats pourraient être obtenus dans n’importe quel langage de programmation, que ce soit Python, Java, JavaScript, C#, F# ou un autre. Mon propos est qu’il faudrait simplement écrire plus de lignes de code, c’est pourquoi je reste avec Envision. Tous les extraits de code présentés ici dans cette conférence et, d’ailleurs, dans les précédentes, sont autonomes et complets. Techniquement, vous pourriez copier et coller ce code et il s’exécuterait. Il n’y a aucun module impliqué, aucun code caché, et aucun environnement à configurer.

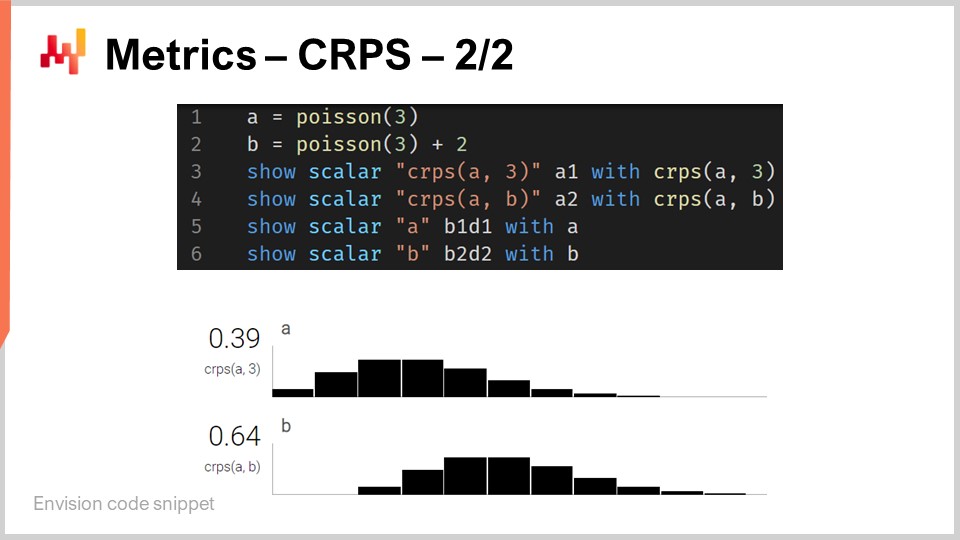
Revenons donc à l’extrait de code. Aux lignes un et deux, nous définissons des distributions unidimensionnelles. Je reviendrai sur le fonctionnement de ces distributions unidimensionnelles dans Envision, mais nous avons ici deux distributions : l’une est une distribution de Poisson, qui est une distribution discrète unidimensionnelle, et la deuxième, à la ligne deux, est la même distribution de Poisson mais décalée de deux unités vers la droite. C’est ce que signifie le “+2”. À la ligne trois, nous calculons la distance CRPS entre une distribution et la valeur 3, qui est un nombre. Ici, nous relevons cette asymétrie en termes de types de données dont je parlais. Ensuite, les résultats s’affichent en bas, comme vous pouvez le constater.

À la ligne quatre, nous calculons le CRPS entre la distribution A et la distribution B. Bien que la définition classique du CRPS se situe entre une distribution et un seul point, il est tout à fait aisé de généraliser cette définition à une paire de distributions. Il suffit de reprendre la même formule du CRPS et de remplacer la fonction échelon de Heaviside par la fonction de distribution cumulative de la seconde distribution. Les instructions “show” des lignes trois à six aboutissent à l’affichage que vous pouvez voir en bas de l’écran, qui est littéralement une capture d’écran.

Nous constatons ainsi que l’utilisation du CRPS n’est ni plus difficile ni plus compliquée que l’utilisation de toute fonction spéciale, comme la fonction cosinus. Évidemment, cela peut s’avérer un peu contraignant si vous devez réimplémenter le cosinus vous-même, mais, dans l’ensemble, il n’y a rien de particulièrement compliqué avec le CRPS. Passons maintenant à la suite.

Le problème de Monge-Kantorovich nous éclaire sur la manière d’aborder le processus d’appariement de formes impliqué dans le CRPS mais en dimensions supérieures. Rappelez-vous que le CRPS est en réalité confiné à la dimension un. L’appariement de formes est, en concept, quelque chose qui pourrait être généralisé à un nombre quelconque de dimensions, et le problème de Monge-Kantorovich est très intéressant, d’autant plus qu’à la base, il s’agit en fait d’un problème de supply chain.

Le problème de Monge-Kantorovich, initialement sans lien avec la prévision probabiliste, a été introduit par le scientifique français Gaspard Monge dans un mémoire de 1781 intitulé “Mémoire sur la théorie des déblais et des remblais”, que l’on pourrait approximativement traduire par “Mémoire sur la théorie du déplacement de la terre”. Une manière de comprendre le problème de Monge-Kantorovich est d’imaginer une situation où nous disposons d’une liste de mines, désignée par M à l’écran, et d’une liste d’usines, désignée par F. Les mines extraient du minerai, et les usines en consomment. Ce que nous voulons, c’est construire un plan de transport, T, qui associe l’ensemble du minerai produit par les mines à la consommation requise par les usines.

Monge définissait le capital C comme le coût nécessaire pour transporter tout le minerai des mines vers les usines. Le coût correspond à la somme nécessaire pour déplacer tout le minerai de chaque mine vers chaque usine, mais il existe évidemment des méthodes de transport très inefficaces. Ainsi, lorsque nous évoquons un coût spécifique, nous entendons que ce coût reflète le plan de transport optimal. Ce capital C représente le meilleur coût réalisable en tenant compte du plan de transport optimal.

Il s’agit essentiellement d’un problème de supply chain qui a été étudié de manière approfondie au fil des siècles. Dans la formulation complète du problème, il existe des contraintes sur T. Par souci de concision, je n’ai pas affiché toutes les contraintes à l’écran. Il y a, par exemple, une contrainte selon laquelle le plan de transport ne doit pas dépasser la capacité de production de chaque mine, et chaque usine doit être entièrement satisfaite, en recevant une allocation correspondant à ses exigences. Il y a beaucoup de contraintes, mais comme elles sont assez verbeuses, je ne les ai pas incluses à l’écran.

Maintenant, bien que le problème de transport soit intéressant en lui-même, si nous commençons à interpréter la liste des mines et la liste des usines comme deux distributions de probabilité, nous disposons d’un moyen de transformer une métrique ponctuelle en une métrique distributive. C’est un aperçu clé du couplage de formes en dimensions supérieures à travers la perspective de Monge-Kantorovich. Un autre terme pour cette perspective est la métrique de Wasserstein, bien qu’elle concerne principalement le cas non discret, qui est de moindre intérêt pour nous.

La perspective de Monge-Kantorovich nous permet de transformer une métrique ponctuelle, capable de calculer la différence entre deux nombres ou deux vecteurs de nombres, en une métrique qui s’applique aux distributions de probabilité opérant dans le même espace. C’est un mécanisme très puissant. Cependant, le problème de Monge-Kantorovich est difficile à résoudre et nécessite une puissance de traitement considérable. Pour le reste de la conférence, je me contenterai de techniques plus simples à mettre en œuvre et à exécuter.

La perspective bayésienne consiste à examiner une série d’observations du point de vue d’une croyance a priori. La perspective bayésienne est généralement comprise en opposition à la perspective fréquentiste, qui estime la fréquence des résultats sur la base des observations réelles. L’idée est que la perspective fréquentiste ne s’accompagne pas de croyances a priori. Ainsi, la perspective bayésienne nous donne un outil connu sous le nom de vraisemblance pour évaluer le degré de surprise en considérant les observations et un modèle donné. Le modèle, qui est essentiellement un modèle de prévision probabiliste, est la formalisation de nos croyances a priori. La perspective bayésienne nous donne un moyen d’évaluer un ensemble de données par rapport à un modèle de prévision probabiliste. Pour comprendre comment cela est fait, nous devons commencer par la vraisemblance pour un seul point de donnée. La vraisemblance, lorsqu’on a une observation x, est la probabilité d’observer x selon le modèle. Ici, on suppose que le modèle est entièrement caractérisé par theta, les paramètres du modèle. La perspective bayésienne suppose généralement que le modèle a une forme paramétrique, et theta est le vecteur complet de tous les paramètres du modèle.

Lorsque nous disons theta, nous supposons implicitement que nous disposons d’une caractérisation complète du modèle probabiliste, qui nous donne une densité de probabilité locale pour tous les points. Ainsi, la vraisemblance est la probabilité d’observer ce point de donnée. Lorsque nous avons la vraisemblance pour le modèle theta, c’est la probabilité conjointe d’observer tous les points de données de l’ensemble. Nous supposons que ces points sont indépendants, de sorte que la vraisemblance est un produit de probabilités.

Si nous avons des milliers d’observations, la vraisemblance, en tant que produit de milliers de valeurs inférieures à un, est susceptible d’être numériquement infiniment petite. Une valeur infiniment petite est généralement difficile à représenter avec la manière dont les nombres à virgule flottante sont représentés dans les ordinateurs. Au lieu de travailler directement avec la vraisemblance, qui est un nombre infiniment petit, nous avons tendance à utiliser la log-vraisemblance. La log-vraisemblance est simplement le logarithme de la vraisemblance, qui a l’incroyable propriété de transformer la multiplication en addition.

La log-vraisemblance du modèle theta est la somme du logarithme de toutes les vraisemblances individuelles pour chacun des points de données, comme le montre la dernière ligne d’équation à l’écran. La vraisemblance est une métrique qui nous donne une qualité d’ajustement pour une prévision probabiliste donnée. Elle nous indique la probabilité que le modèle ait généré l’ensemble de données que nous finissons par observer. Si nous avons deux prévisions probabilistes en compétition, et si nous mettons de côté tous les autres problèmes d’ajustement un instant, nous devrions choisir le modèle qui nous donne la vraisemblance la plus élevée ou la log-vraisemblance la plus élevée, car plus c’est élevé, mieux c’est.

La vraisemblance est très intéressante car elle peut fonctionner en haute dimension sans complications, contrairement à la méthode de Monge-Kantorovich. Tant que nous disposons d’un modèle qui nous offre une densité de probabilité locale, nous pouvons utiliser la vraisemblance, ou plus précisément, la log-vraisemblance comme métrique.

De plus, dès que nous disposons d’une métrique pouvant représenter la qualité d’ajustement, cela signifie que nous pouvons optimiser en fonction de cette métrique même. Il suffit d’un modèle avec au moins un degré de liberté, ce qui signifie fondamentalement au moins un paramètre. Si nous optimisons ce modèle par rapport à la vraisemblance, notre métrique d’ajustement, nous obtiendrons, espérons-le, un modèle entraîné dans lequel nous avons appris à produire au moins une prévision probabiliste correcte. C’est exactement ce qui est fait ici à l’écran.

Aux lignes un et deux, nous générons un jeu de données simulé. Nous créons une table avec 2 000 lignes, puis à la ligne deux, nous générons 2 000 déviations, nos observations issues d’une distribution de Poisson avec une moyenne de deux. Ainsi, nous avons nos 2 000 observations. À la ligne trois, nous démarrons un bloc autodiff, qui fait partie du paradigme de programmation différentiable. Ce bloc exécutera une descente de gradient stochastique et itérera de nombreuses fois sur toutes les observations de la table d’observations. Ici, la table d’observations est la table T.

À la ligne quatre, nous déclarons le paramètre unique du modèle, appelé lambda. Nous indiquons que ce paramètre doit être exclusivement positif. Ce paramètre est ce que nous essaierons de redécouvrir grâce à la descente de gradient stochastique. À la ligne cinq, nous définissons la fonction de perte, qui est simplement l’opposé de la log-vraisemblance. Nous voulons maximiser la vraisemblance, mais le bloc autodiff tente de minimiser la perte. Ainsi, si nous voulons maximiser la log-vraisemblance, nous devons ajouter ce signe négatif devant la log-vraisemblance, ce que nous avons exactement fait.

Le paramètre lambda appris est affiché à la ligne six. Sans surprise, la valeur trouvée est très proche de la valeur deux, car nous avons commencé avec une distribution de Poisson ayant une moyenne de deux. Nous avons créé un modèle de prévision probabiliste qui est également paramétrique et de la même forme, une distribution de Poisson. Nous voulions redécouvrir le paramètre unique de la distribution de Poisson, et c’est exactement ce que nous avons obtenu. Nous obtenons un modèle qui se situe à environ un pour cent de l’estimation initiale.

Nous venons d’apprendre notre premier modèle de prévision probabiliste, et tout cela a essentiellement nécessité trois lignes de code. C’est évidemment un modèle très simple ; néanmoins, cela montre qu’il n’y a rien d’intrinsèquement compliqué dans la prévision probabiliste. Ce n’est pas votre prévision au sens classique du carré moyen, mais mis à part cela, avec les bons outils comme la programmation différentiable, ce n’est pas plus compliqué qu’une prévision ponctuelle classique.

La fonction log_likelihood.poisson que nous avons utilisée précédemment fait partie de la bibliothèque standard d’Envision. Cependant, il n’y a aucune magie impliquée. Regardons comment cette fonction est réellement implémentée dans les coulisses. Les deux premières lignes en haut nous donnent l’implémentation de la log-vraisemblance de la distribution de Poisson. Une distribution de Poisson est entièrement caractérisée par son unique paramètre, lambda, et la fonction de log-vraisemblance ne prend que deux arguments : le paramètre qui caractérise entièrement la distribution de Poisson et l’observation réelle. La formule que j’ai écrite est littéralement tirée d’un manuel. C’est ce que vous obtenez lorsque vous implémentez la formule du manuel qui caractérise la distribution de Poisson. Il n’y a rien de sophistiqué ici.

Faites attention au fait que cette fonction est marquée avec le mot-clé autodiff. Comme nous l’avons vu dans la conférence précédente, le mot-clé autodiff garantit que la différentiation automatique peut se propager correctement à travers cette fonction. La log-vraisemblance de la distribution de Poisson utilise également une autre fonction spéciale, log_gamma. La fonction log_gamma est le logarithme de la fonction gamma, qui est la généralisation de la fonction factorielle aux nombres complexes. Ici, nous n’avons besoin que de la généralisation de la fonction factorielle aux nombres réels positifs.

L’implémentation de la fonction log_gamma est légèrement verbeuse, mais c’est encore du matériel de manuel. Elle utilise une approximation par fraction continue pour la fonction log_gamma. L’astuce ici est que nous avons la différentiation automatique qui fonctionne pour nous jusque-là. Nous commençons avec le bloc autodiff, appelant la fonction log_likelihood.poisson, qui est implémentée comme une fonction autodiff. Cette fonction, à son tour, appelle la fonction log_gamma, également implémentée avec le marqueur autodiff. Essentiellement, nous sommes capables de produire nos méthodes de prévision probabilistes en trois lignes de code parce que nous disposons d’une bibliothèque standard bien conçue qui a été implémentée, en prêtant attention à la différentiation automatique.

Passons maintenant au cas particulier des distributions discrètes unidimensionnelles. Ces distributions se retrouvent partout dans une supply chain et représentent notre point d’entrée dans la prévision probabiliste. Par exemple, si nous voulons prévoir les délais d’approvisionnement avec une granularité quotidienne, nous pouvons dire qu’il y a une certaine probabilité d’avoir un délai d’un jour, une autre probabilité d’avoir un délai de deux jours, trois jours, et ainsi de suite. Tout cela se constitue en un histogramme de probabilités pour les délais d’approvisionnement. De même, si nous examinons la demande pour un SKU donné un jour donné, nous pouvons dire qu’il y a une probabilité d’observer zéro unité de demande, une unité de demande, deux unités de demande, et ainsi de suite.

Si nous regroupons toutes ces probabilités, nous obtenons un histogramme qui les représente. De même, si nous pensons au niveau de stocks d’un SKU, nous pourrions être intéressés à évaluer combien de stocks resteront pour ce SKU à la fin de la saison. Nous pouvons utiliser une prévision probabiliste pour déterminer la probabilité d’avoir zéro unité en stock à la fin de la saison, une unité en stock, deux unités, et ainsi de suite. Toutes ces situations correspondent à un schéma qui se représente à travers un histogramme avec des compartiments associés à chaque résultat discret du phénomène d’intérêt.

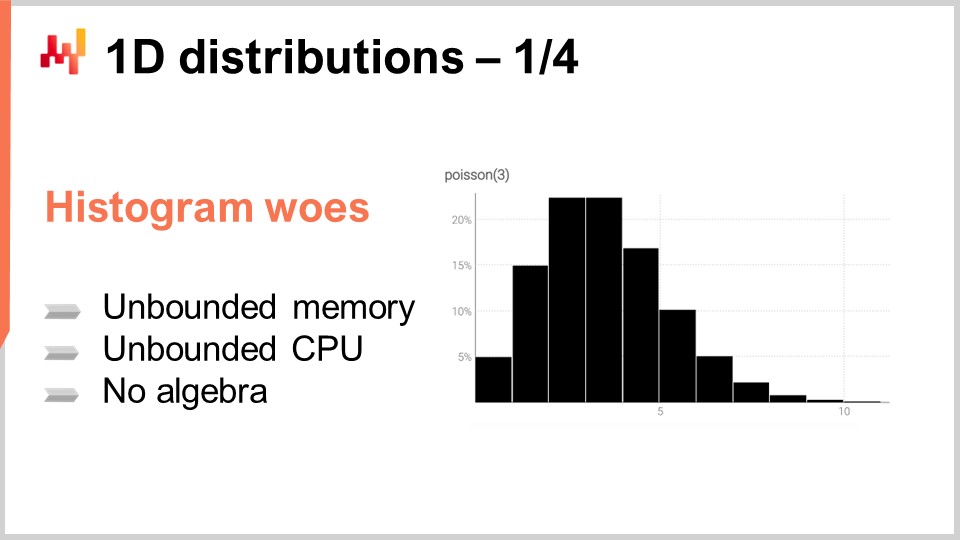
L’histogramme est la manière canonique de représenter une distribution discrète unidimensionnelle. Chaque compartiment est associé à la masse de probabilité pour le résultat discret. Cependant, en mettant de côté l’utilisation en visualisation de données, les histogrammes sont quelque peu décevants. En effet, travailler avec des histogrammes est un peu laborieux si nous voulons faire autre chose que visualiser ces distributions de probabilité. Nous avons essentiellement deux catégories de problèmes avec les histogrammes : le premier problème est lié aux ressources informatiques, et la deuxième catégorie de problèmes est liée à l’expressivité en programmation des histogrammes.

En termes de ressources informatiques, nous devons considérer que la quantité de mémoire nécessaire à un histogramme est fondamentalement illimitée. Vous pouvez considérer un histogramme comme un tableau qui s’agrandit autant que nécessaire. Lorsqu’il s’agit d’un seul histogramme, même exceptionnellement grand du point de vue de la supply chain, la quantité de mémoire requise n’est pas un problème pour un ordinateur moderne. Le problème survient lorsque vous avez non pas un seul histogramme, mais des millions d’histogrammes pour des millions de SKUs dans un contexte de supply chain. Si chaque histogramme peut devenir assez grand, la gestion de ces histogrammes peut devenir un défi, surtout si l’on considère que les ordinateurs modernes tendent à offrir un accès mémoire non uniforme.

Inversement, la quantité de CPU nécessaire pour traiter ces histogrammes est également illimitée. Bien que les opérations sur les histogrammes soient principalement linéaires, le temps de traitement augmente avec la croissance de la mémoire en raison de l’accès mémoire non uniforme. Par conséquent, il existe un intérêt significatif à imposer des limites strictes sur la quantité de mémoire et de CPU requise.

Le second problème avec les histogrammes est l’absence d’algèbre qui leur soit associée. Bien que vous puissiez effectuer une addition ou une multiplication compartiment par compartiment lorsque vous considérez deux histogrammes, cela ne donnera pas un résultat cohérent lorsqu’on interprète l’histogramme comme une représentation d’une variable aléatoire. Par exemple, si vous prenez deux histogrammes et effectuez une multiplication point par point, vous obtenez un histogramme qui n’a même pas une masse de un. Ce n’est pas une opération valide du point de vue d’une algèbre des variables aléatoires. Vous ne pouvez pas vraiment additionner ou multiplier des histogrammes, de sorte que vous êtes limité dans ce que vous pouvez en faire.

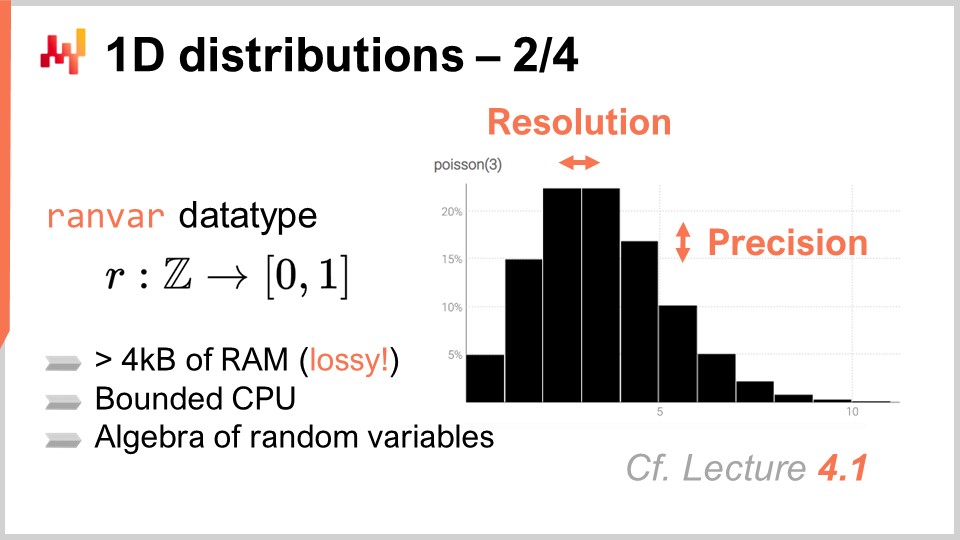
Chez Lokad, l’approche que nous avons trouvée la plus pratique pour traiter ces distributions discrètes unidimensionnelles omniprésentes est d’introduire un type de données dédié. Le public connaît probablement les types de données courants présents dans la plupart des langages de programmation, tels que les entiers, les nombres à virgule flottante et les chaînes de caractères. Ce sont les types de données primitifs typiques que l’on retrouve partout. Cependant, rien ne vous empêche d’introduire des types de données plus spécialisés, particulièrement adaptés à nos exigences depuis une perspective de supply chain. C’est exactement ce que Lokad a fait avec le type de données ranvar.

Le type de données ranvar est dédié aux distributions discrètes unidimensionnelles, et le nom est une abréviation de variable aléatoire. Techniquement, du point de vue formel, le ranvar est une fonction de Z (l’ensemble de tous les entiers, positifs et négatifs) vers des probabilités, qui sont des nombres compris entre zéro et un. La masse totale de Z est toujours égale à un, puisqu’elle représente des distributions de probabilité.

D’un point de vue purement mathématique, certains pourraient soutenir que la quantité d’informations pouvant être intégrées dans une telle fonction peut devenir arbitrairement grande. Cela est vrai ; cependant, la réalité est que, du point de vue de la supply chain, il existe une limite très claire quant à la quantité d’informations pertinentes pouvant être contenues dans un seul ranvar. Bien qu’il soit théoriquement possible de concevoir une distribution de probabilité nécessitant des mégaoctets pour être représentée, aucune distribution de ce type n’existe qui soit pertinente pour les besoins de la supply chain.

Il est possible de concevoir une borne supérieure de 4 kilobytes pour le type de données ranvar. En limitant la mémoire que ce ranvar peut utiliser, nous obtenons également une borne supérieure au niveau du CPU pour toutes les opérations, ce qui est très important. Au lieu d’avoir une limite naïve plafonnant les compartiments à 1,000, Lokad introduit un schéma de compression avec le type de données ranvar. Cette compression est essentiellement une représentation avec perte des données originales, perdant en résolution et en précision. Cependant, l’idée est de concevoir un schéma de compression qui fournisse une représentation suffisamment précise des histogrammes, de sorte que le degré d’approximation introduit soit négligeable du point de vue de la supply chain.

La fine print de l’algorithme de compression impliqué avec le type de données ranvar dépasse le cadre de cette conférence. Cependant, il s’agit d’un algorithme de compression très simple qui est d’ordres de grandeur plus simple que les types d’algorithmes de compression utilisés pour les images sur votre ordinateur. En outre, en limitant la mémoire que ce ranvar peut utiliser, nous obtenons également une borne supérieure au niveau du CPU pour toutes les opérations, ce qui est très important. Enfin, avec le type de données ranvar, le point le plus important est que nous obtenons une algèbre de variables qui nous permet de manipuler ces types de données et de faire tout ce que nous voulons faire avec des types de données primitifs, c’est-à-dire disposer de toutes sortes de primitives pour les combiner de manière à répondre à nos exigences.

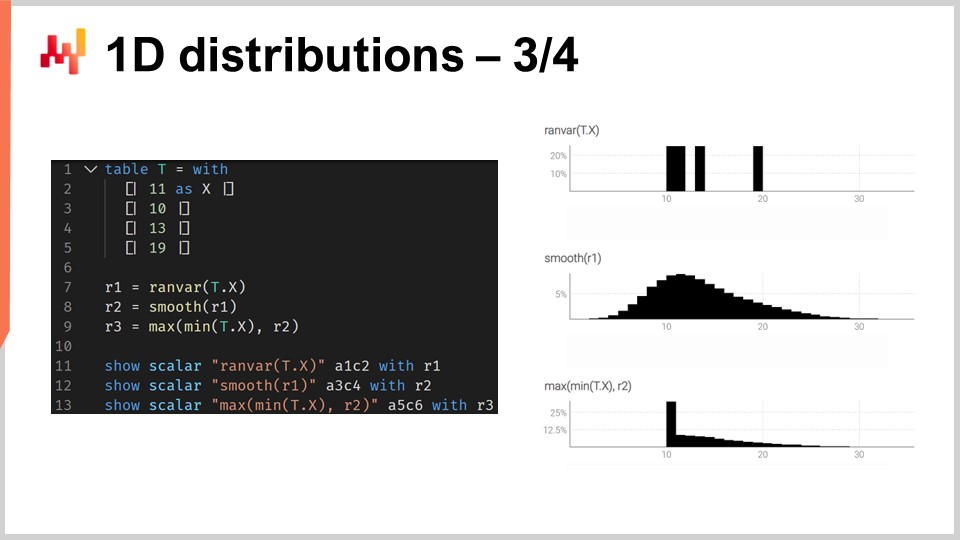
Pour illustrer ce que signifie travailler avec des ranvars, considérons une situation de prévision des délais, plus précisément, une prévision probabiliste d’un délai. À l’écran se trouve un court script Envision qui montre comment construire une telle prévision probabiliste. Aux lignes 1-5, nous introduisons la table T qui contient les quatre délais de variation, avec des valeurs de 11 jours, 10 jours, 13 jours et 90 jours. Bien que quatre observations soient très peu, il est malheureusement très courant d’avoir un nombre de points de données très limité en ce qui concerne les observations de délais. En effet, si nous considérons un fournisseur étranger qui reçoit deux bons de commande par an, il faut alors deux ans pour collecter ces quatre points de données. Ainsi, il est important de disposer de techniques capables de fonctionner même avec un ensemble d’observations incroyablement limité.

À la ligne 7, nous créons un ranvar en agrégant directement les quatre observations. Ici, le terme “ranvar” qui apparaît à la ligne 7 est en fait un agrégateur qui prend une série de nombres en entrée et renvoie une seule valeur du type de données ranvar. Le résultat est affiché en haut à droite de l’écran, ce qui correspond à un ranvar empirique.

Cependant, ce ranvar empirique n’est pas une représentation réaliste de la distribution réelle. Par exemple, bien que nous puissions observer un délai de 11 jours et un délai de 13 jours, il semble irréaliste de ne pas pouvoir observer un délai de 12 jours. Si nous interprétons ce ranvar comme une prévision probabiliste, il indiquerait que la probabilité d’observer un délai de 12 jours est nulle, ce qui semble incorrect. Il s’agit évidemment d’un problème de surapprentissage.

Pour remédier à cette situation, à la ligne 8, nous lissons le ranvar original en appelant la fonction “smooth”. La fonction smooth remplace essentiellement le ranvar original par un mélange de distributions. Pour chaque compartiment de la distribution originale, nous le remplaçons par une distribution de Poisson dont la moyenne est centrée sur le compartiment, pondérée selon la probabilité respective des compartiments. Grâce à la distribution lissée, nous obtenons l’histogramme affiché au centre à droite de l’écran. Cela a déjà l’air beaucoup mieux ; nous n’avons plus d’écarts bizarres et nous n’avons plus de probabilité nulle au milieu. De plus, en regardant la probabilité d’observer un délai de 12 jours, ce modèle nous donne une probabilité non nulle, ce qui paraît bien plus raisonnable. Il nous donne également une probabilité non nulle d’aller au-delà de 20 jours, et compte tenu du fait que nous avons eu quatre points de données et avons déjà observé un délai de 19 jours, l’idée qu’un délai aussi élevé que 20 jours soit possible paraît très raisonnable. Ainsi, avec cette prévision probabiliste, nous disposons d’une répartition convenable qui représente une probabilité non nulle pour ces événements, ce qui est très bien.

Cependant, à gauche, nous avons quelque chose d’un peu étrange. Alors qu’il est acceptable que cette distribution de probabilité s’étende vers la droite, il en va autrement pour la gauche. Si nous considérons que les délais observés résultaient des temps de transport, étant donné qu’il faut neuf jours pour que le camion arrive, il semble peu probable d’observer un délai de trois jours. À cet égard, le modèle est assez irréaliste.

Ainsi, à la ligne 9, nous introduisons un ranvar conditionnellement ajusté en précisant qu’il doit être supérieur au plus petit délai jamais observé. Nous utilisons “min_of(T, x)” qui prend la plus petite valeur parmi les nombres de la table T, puis nous utilisons “max” pour effectuer le maximum entre une distribution et un nombre. Le résultat doit être supérieur à cette valeur. Le ranvar ajusté est affiché à droite, tout en bas, et nous voyons ici notre prévision finale du délai. Cette dernière ressemble à une prévision probabiliste très raisonnable du délai, considérant que nous disposons d’un ensemble de données incroyablement limité avec seulement quatre points de données. Nous ne pouvons pas dire qu’il s’agit d’une excellente prévision probabiliste ; cependant, j’affirmerais qu’il s’agit d’une prévision de niveau production, et ce genre de techniques fonctionnerait bien en production, contrairement à une prévision moyenne par point qui sous-estimerait largement le risque de délais variables.

La beauté des prévisions probabilistes réside dans le fait que, bien qu’elles puissent être très rudimentaires, elles offrent déjà un certain potentiel d’atténuation pour des décisions mal informées qui résulteraient de l’application naïve d’une prévision moyenne basée sur les données observées.

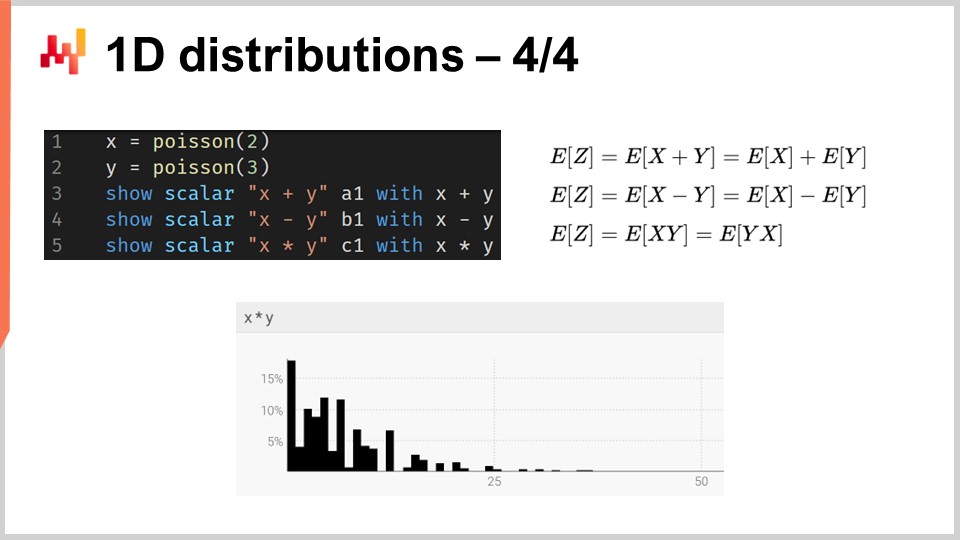
De manière plus générale, les ranvars supportent une large gamme d’opérations : il est possible d’additionner, de soustraire et de multiplier des ranvars, tout comme il est possible d’additionner, de soustraire et de multiplier des entiers. En interne, parce que nous traitons avec des variables aléatoires discrètes en termes de sémantique, toutes ces opérations sont implémentées comme des convolutions. À l’écran, l’histogramme affiché en bas est obtenu par la multiplication de deux distributions de Poisson, respectivement de moyenne deux et trois. Dans la supply chain, la multiplication de variables aléatoires est appelée une convolution directe. Dans le contexte de la supply chain, la multiplication de deux variables aléatoires permet de représenter, par exemple, les résultats que vous pouvez obtenir lorsque les clients recherchent les mêmes produits mais avec des multiplicateurs variables. Supposons que nous ayons une librairie qui sert deux cohortes de clients. D’un côté, nous avons la première cohorte composée d’étudiants, qui achètent une unité lorsqu’ils entrent dans le magasin. Dans cette librairie illustrative, nous avons une deuxième cohorte composée de professeurs, qui achètent 20 livres lorsqu’ils entrent dans le magasin.

D’un point de vue de modélisation, nous pourrions disposer d’une prévision probabiliste qui représente les taux d’arrivée dans la librairie, que ce soit pour les étudiants ou pour les professeurs. Cela nous donnerait la probabilité d’observer zéro client pour la journée, un client, deux clients, etc., révélant la distribution de probabilité d’observer un certain nombre de clients pour une journée donnée. La deuxième variable vous donnerait les probabilités respectives d’acheter une unité (pour les étudiants) par rapport à acheter 20 (pour les professeurs). Pour obtenir une représentation de la demande, nous multiplierions simplement ces deux variables aléatoires, ce qui donnerait un histogramme apparemment erratique qui reflète les multiplicateurs présents dans les schémas de consommation de vos cohortes.

Les générateurs Monte Carlo, ou simplement générateurs, représentent une approche alternative à la prévision probabiliste. Au lieu de présenter une distribution qui nous donne la densité de probabilité locale, nous pouvons présenter un générateur qui, comme son nom l’indique, produit des résultats censés suivre implicitement les mêmes distributions de probabilité locales. Il existe une dualité entre les générateurs et les densités de probabilité, ce qui signifie que les deux sont essentiellement deux facettes d’une même perspective.

Si vous disposez d’un générateur, il est toujours possible de moyenner les résultats obtenus par ce générateur afin de reconstituer des estimations des densités de probabilité locales. Inversement, si vous disposez de densités de probabilité locales, il est toujours possible de tirer des déviations selon cette distribution. Fondamentalement, ces deux approches ne sont que des manières différentes d’envisager la même nature probabiliste ou stochastique du phénomène que nous essayons de modéliser.

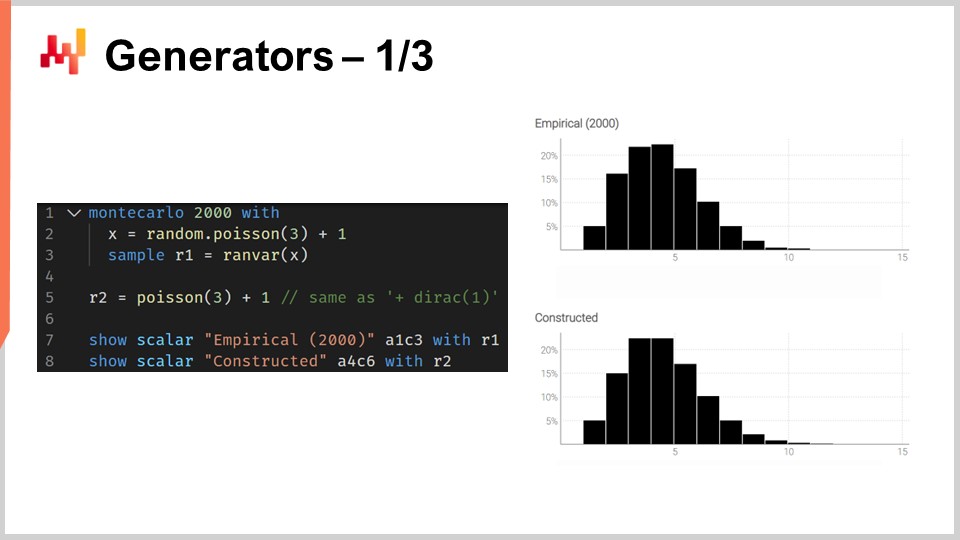
Le script à l’écran illustre cette dualité. À la ligne un, nous introduisons un bloc Monte Carlo, qui sera itéré par le système, tout comme les blocs d’auto-différentiation sont itérés à travers de nombreuses étapes de descente de gradient stochastique. Le bloc Monte Carlo sera exécuté 2,000 fois, et à partir de ce bloc, nous recueillerons 2,000 déviations.

À la ligne deux, nous tirons une déviation d’une distribution de Poisson de moyenne trois, puis ajoutons un à la déviation. Essentiellement, nous obtenons un nombre aléatoire à partir de cette distribution de Poisson puis ajoutons un. À la ligne trois, nous collectons cette déviation dans L1, qui sert d’accumulateur pour l’agrégateur ranvar. Il s’agit du même agrégateur que celui que nous avons introduit précédemment pour notre exemple de délai. Ici, nous rassemblons toutes ces observations dans L1, ce qui nous donne une distribution unidimensionnelle obtenue par un processus Monte Carlo. À la ligne cinq, nous construisons exactement la même distribution discrète unidimensionnelle, mais cette fois, nous le faisons avec l’algèbre des variables aléatoires. Ainsi, nous utilisons simplement Poisson moins trois et ajoutons un. À la ligne cinq, il n’y a pas de processus Monte Carlo en cours ; il s’agit purement de probabilités discrètes et de convolutions.

Lorsque nous comparons visuellement les deux distributions aux lignes sept et huit, nous constatons qu’elles sont presque identiques. Je dis “presque” parce que, bien que nous utilisions 2,000 itérations, ce qui est beaucoup, ce n’est pas infini. Les écarts entre les probabilités exactes obtenues avec le ranvar et les probabilités approximatives obtenues avec le processus Monte Carlo sont encore perceptibles, bien que pas importants.

Les générateurs sont parfois appelés simulateurs, mais ne vous méprenez pas, ils sont la même chose. Chaque fois que vous avez un simulateur, vous avez un processus génératif qui sous-tend implicitement un processus de prévision probabiliste. Chaque fois qu’un simulateur ou un générateur est impliqué, la question qui devrait vous venir à l’esprit est : quelle est la précision de cette simulation ? Elle n’est pas précise par conception, tout comme il est tout à fait possible d’avoir des prévisions complètement inexactes, qu’elles soient probabilistes ou non. Il est très facile d’obtenir une simulation complètement inexacte.

Grâce aux générateurs, nous voyons que les simulations ne sont qu’une manière d’aborder la perspective de la prévision probabiliste, mais cela relève plus d’un détail technique. Cela ne change rien au fait qu’en fin de compte, vous souhaitez disposer de quelque chose qui soit une représentation fidèle du système que vous essayez de caractériser avec votre prévision, qu’elle soit probabiliste ou non.

L’approche générative n’est pas seulement très utile, comme nous le verrons avec un exemple spécifique dans une minute, mais elle est également conceptuellement plus facile à comprendre, du moins légèrement, comparée à l’approche avec les densités de probabilité. Cependant, l’approche Monte Carlo n’est pas non plus exempte de subtilités techniques. Il y a quelques éléments nécessaires si vous souhaitez rendre cette approche viable dans un contexte de production pour une véritable supply chain du monde réel.

Premièrement, les générateurs doivent être rapides. Monte Carlo est toujours un trade-off entre le nombre d’itérations que vous souhaiteriez avoir et le nombre d’itérations que vous pouvez vous permettre, en fonction des ressources informatiques disponibles. Oui, les ordinateurs modernes disposent de beaucoup de puissance de calcul, mais les processus Monte Carlo peuvent être incroyablement gourmands en ressources. Vous voulez quelque chose qui soit, par défaut, super rapide. Si nous revenons aux ingrédients introduits dans la deuxième conférence du quatrième chapitre, nous disposons de fonctions très rapides comme ExhaustShift ou WhiteHash qui sont essentielles à la construction des primitives qui vous permettent de générer des générateurs aléatoires élémentaires ultra-rapides. Vous en avez besoin, sinon, vous allez rencontrer des difficultés. Deuxièmement, vous devez distribuer votre exécution. L’implémentation naïve d’un programme Monte Carlo consiste simplement à avoir une boucle qui s’itère séquentiellement. Cependant, si vous n’utilisez qu’un seul CPU pour répondre à vos exigences Monte Carlo, en essence, vous revenez à la puissance de calcul qui caractérisait les ordinateurs il y a deux décennies. Ce point a été abordé dans la toute première conférence du quatrième chapitre. Au cours des deux dernières décennies, les ordinateurs sont devenus plus puissants, mais principalement en ajoutant des CPU et des degrés de parallélisation. Ainsi, vous devez adopter une perspective distribuée pour vos générateurs.

Enfin, l’exécution doit être déterministe. Qu’est-ce que cela signifie ? Cela signifie que si le même code est exécuté deux fois, il doit donner exactement les mêmes résultats. Cela peut sembler contre-intuitif car nous traitons avec des méthodes aléatoires. Néanmoins, le besoin de déterminisme s’est fait sentir très rapidement. Cela a été découvert de manière douloureuse dans les années 90 lorsque la finance a commencé à utiliser des générateurs Monte Carlo pour leur tarification. La finance s’était tournée vers la prévision probabiliste il y a bien longtemps et faisait un usage intensif des générateurs Monte Carlo. L’une des choses qu’ils ont apprises est que sans déterminisme, il devient presque impossible de reproduire les conditions qui ont généré un bug ou un crash. Du point de vue de la supply chain, des erreurs dans les calculs des bons de commande peuvent s’avérer incroyablement coûteuses.

Si vous souhaitez atteindre un certain degré de préparation à la production pour le logiciel qui régit votre supply chain, vous devez disposer de cette propriété déterministe chaque fois que vous traitez avec Monte Carlo. Sachez que de nombreuses solutions open-source proviennent du milieu académique et ne se préoccupent pas du tout de la préparation à la production. Assurez-vous que lorsque vous traitez avec Monte Carlo, votre processus soit, par défaut, ultra-rapide, distribué par conception et déterministe, afin que vous ayez la possibilité de diagnostiquer les bugs qui apparaîtront inévitablement au fil du temps dans votre environnement de production.

Nous avons vu une situation où un générateur a été introduit pour répliquer ce qui était autrement réalisé avec un ranvar. En règle générale, chaque fois que vous pouvez vous contenter de simples densités de probabilité avec des variables aléatoires sans impliquer Monte Carlo, c’est préférable. Vous obtenez des résultats plus précis, et vous n’avez pas à vous soucier de la stabilité numérique, qui est toujours un peu délicate avec Monte Carlo. Cependant, l’expressivité de l’algèbre des variables aléatoires est limitée, et c’est là que Monte Carlo brille vraiment. Ces générateurs sont plus expressifs car ils vous permettent d’appréhender des situations qui ne peuvent être abordées avec seulement une algèbre des variables aléatoires.

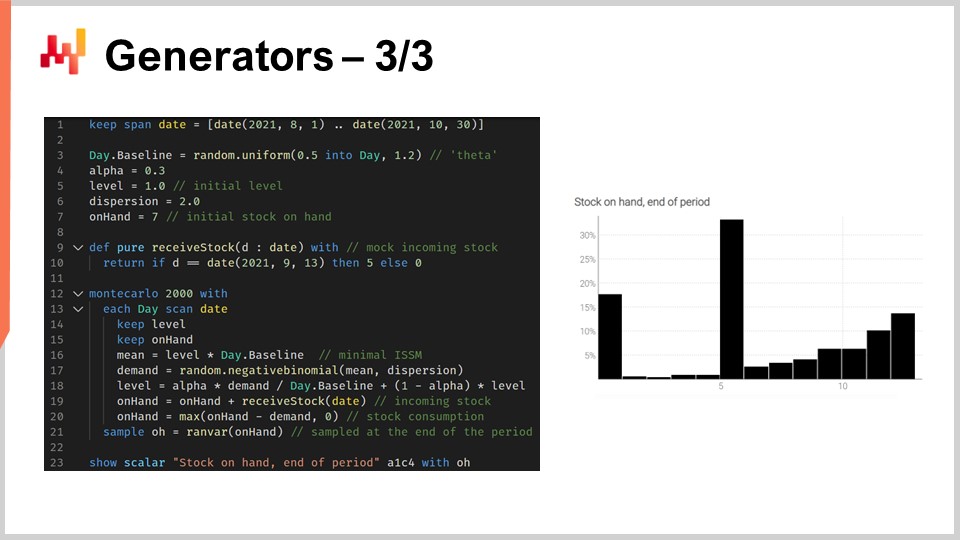
Illustrons cela avec une situation de supply chain. Considérons un SKU unique avec un niveau initial de stocks, une prévision probabiliste pour la demande, et une période d’intérêt s’étalant sur trois mois, avec un arrivage en cours de période. Nous partons du principe que la demande est soit satisfaite immédiatement à partir des stocks disponibles, soit perdue définitivement. Nous souhaitons connaître le niveau de stocks attendu à la fin de la période pour le SKU, car cela nous aidera à déterminer le risque encouru en termes de stocks morts.

La situation est traître car elle a été conçue de manière à offrir une troisième possibilité pour qu’une rupture de stock se produise en plein milieu de la période. L’approche naïve consisterait à prendre le niveau initial de stocks, la distribution de la demande pour l’ensemble de la période, et à soustraire la demande de ce niveau, ce qui donnerait le stock restant. Toutefois, cela ne prend pas en compte le fait que nous pourrions perdre une partie non négligeable de la demande si nous subissons une rupture de stock alors que le replenishment attendu n’est pas encore arrivé. Une telle approche naïve sous-estimerait la quantité de stocks que nous aurons à la fin de la période et surestimerait la demande qui serait satisfaite.

Le script présenté modélise l’occurrence des ruptures de stock afin que nous disposions d’un estimateur correct du niveau de stocks pour ce SKU à la fin de la période. De la ligne 1 à la ligne 10, nous définissons les données fictives qui caractérisent notre modèle. Les lignes 3 à 6 contiennent les paramètres pour le modèle ISSM. Nous avons déjà vu le modèle ICSM dans la toute première conférence de ce cinquième chapitre. Essentiellement, ce modèle génère une trajectoire de demande avec un point de données par jour. La période d’intérêt est définie dans la table des jours, et nous disposons des paramètres pour cette trajectoire dès le début.

Dans les conférences précédentes, nous avons présenté le modèle AICSM ainsi que les méthodes requises, via la programmation différentiable, pour apprendre ces paramètres. Aujourd’hui, nous utilisons le modèle en supposant avoir appris tout ce qu’il fallait apprendre. À la ligne 7, nous définissons le stock initial disponible, qui serait typiquement obtenu à partir de l’ERP ou du WMS. Aux lignes 9 et 10, nous définissons la quantité et la date pour le replenishment. Ces points de données seraient typiquement obtenus sous forme d’un délai d’arrivée estimé, communiqué par le fournisseur et enregistré dans l’ERP. Nous supposons que la date de livraison est parfaitement connue ; cependant, il serait aisé de remplacer cette date unique par une prévision probabiliste du délai.

De la ligne 12 à la ligne 21, nous avons le modèle ISSM qui génère la trajectoire de demande. Nous sommes dans une boucle Monte Carlo, et pour chaque itération, nous parcourons chaque jour de la période d’intérêt. L’itération des jours commence à la ligne 13. Nous disposons de la mécanique ESSM, mais aux lignes 19 et 20, nous mettons à jour la variable représentant le stock disponible. Cette variable ne fait pas partie intégrante du modèle ISSM ; c’est un élément supplémentaire. À la ligne 19, nous indiquons que le stock disponible est égal au stock d’hier plus l’arrivage, qui sera nul pour la plupart des jours et de cinq unités le 13 septembre. Ensuite, à la ligne 20, nous mettons à jour le stock disponible en indiquant qu’un certain nombre d’unités est consommé par la demande du jour, et nous utilisons max 0 pour signifier que le niveau de stocks ne peut pas devenir négatif.

Enfin, nous recueillons le stock final disponible à la ligne 21, et à la ligne 23, ce stock final est affiché. Voici l’histogramme que vous voyez à droite de l’écran. Nous observons ici une distribution à la forme très irrégulière. Cette forme ne peut être obtenue par l’algèbre des variables aléatoires. Les générateurs sont incroyablement expressifs ; cependant, il ne faut pas confondre leur expressivité avec leur précision. Bien que ces générateurs soient extrêmement expressifs, il est difficile d’évaluer la précision d’un tel dispositif. Ne vous méprenez pas, chaque fois qu’un générateur ou simulateur est utilisé, il s’agit d’une prévision probabiliste, et les simulations peuvent être dramatiquement inexactes, tout comme toute prévision, probabiliste ou non.

La conférence a déjà été longue, et pourtant il y a de nombreux sujets que je n’ai même pas abordés aujourd’hui. La prise de décision, par exemple, si tous les futurs sont possibles, comment décider quoi que ce soit ? Je n’ai pas répondu à cette question, mais elle sera abordée dans la prochaine conférence.

Les dimensions supérieures sont également importantes à considérer. La distribution unidimensionnelle constitue un point de départ, mais une supply chain a besoin de plus. Par exemple, si nous rencontrons une rupture de stock pour un SKU donné, nous pouvons observer une cannibalisation, où les clients se tournent naturellement vers un substitut. Nous aimerions modéliser cela, même de manière sommaire.

Les constructions d’ordre supérieur jouent également un rôle. Comme je l’ai dit, prévoir la demande n’est pas comme prédire les mouvements des planètes. Nous constatons des effets auto-prédictifs partout. À un moment donné, nous voulons prendre en compte et intégrer nos politiques de tarification et de replenishment de stocks. Pour ce faire, nous avons besoin de constructions d’ordre supérieur, ce qui signifie que, donnée une politique, vous obtenez une prévision probabiliste du résultat, mais vous devez injecter la politique à l’intérieur de ces constructions.

De plus, maîtriser les prévisions probabilistes implique de nombreuses méthodes numériques et une expertise sectorielle pour savoir quelles distributions sont les plus susceptibles de s’adapter correctement à certaines situations. Dans cette série de conférences, nous présenterons davantage d’exemples par la suite.

Enfin, il y a le défi du changement. La prévision probabiliste représente un départ radical par rapport aux pratiques conventionnelles de la supply chain. Souvent, les aspects techniques liés aux prévisions probabilistes ne constituent qu’une petite partie du défi. La partie difficile consiste à réinventer l’organisation elle-même, afin qu’elle puisse commencer à utiliser ces prévisions probabilistes au lieu de se fier aux prévisions ponctuelles, qui relèvent essentiellement d’un souhait irréaliste. Tous ces éléments seront abordés dans de futures conférences, mais cela prendra du temps car il y a beaucoup de terrain à couvrir.

En conclusion, les prévisions probabilistes représentent un départ radical par rapport à la perspective des prévisions ponctuelles, où l’on s’attend à un consensus quant à un unique futur censé se réaliser. La prévision probabiliste repose sur l’observation que l’incertitude de l’avenir est irréductible. Un siècle de science de la prévision a démontré que toutes les tentatives visant à obtenir des prévisions même proches de l’exactitude ont échoué. Ainsi, nous nous retrouvons face à de nombreux futurs indéfinis. Cependant, les prévisions probabilistes nous fournissent les techniques et outils pour quantifier et évaluer ces futurs. La prévision probabiliste est une avancée significative. Il a fallu presque un siècle pour accepter l’idée que la prévision économique n’était pas comparable à l’astronomie. Alors que nous pouvons prédire avec une grande précision la position exacte d’une planète dans un siècle, nous n’avons aucun espoir d’obtenir quelque chose de remotement équivalent dans le domaine des supply chain. L’idée de disposer d’une prévision unique pour gouverner toutes les situations ne reviendra tout simplement pas. Pourtant, de nombreuses entreprises s’accrochent encore à l’espoir qu’à un moment donné, la seule prévision vraiment précise sera réalisée. Après un siècle de tentatives, il s’agit essentiellement d’un vœu pieux.

Avec les ordinateurs modernes, cette perspective d’un avenir unique n’est pas la seule envisageable. Nous avons des alternatives. La prévision probabiliste existe depuis les années 90, soit il y a trois décennies. Chez Lokad, nous utilisons la prévision probabiliste pour piloter les supply chains en production depuis plus d’une décennie. Ce n’est peut-être pas encore la norme, mais c’est loin d’être de la science-fiction. Cela fait réalité pour de nombreuses entreprises dans la finance depuis trois décennies et dans le monde de la supply chain depuis une décennie.

Bien que les prévisions probabilistes puissent sembler intimidantes et très techniques, avec les bons outils, il suffit de quelques lignes de code. Il n’y a rien de particulièrement difficile ou complexe à propos de la prévision probabiliste, du moins pas en comparaison avec d’autres types de prévisions. Le plus grand défi en matière de prévision probabiliste est d’abandonner le confort associé à l’illusion que l’avenir est parfaitement sous contrôle. L’avenir n’est pas parfaitement maîtrisé et ne le sera jamais, et tout bien réfléchi, c’est probablement pour le mieux.

Cela conclut la conférence d’aujourd’hui. La prochaine fois, le 6 avril, je présenterai la prise de décision dans la distribution des stocks en retail, et nous verrons comment les prévisions probabilistes présentées aujourd’hui peuvent être mises à profit pour orienter une décision de supply chain basique, à savoir le réapprovisionnement des stocks dans un réseau de retail. La conférence aura lieu le même jour de la semaine, mercredi, à la même heure, 15 heures, et ce sera le premier mercredi d’avril.

Question: Peut-on optimiser la résolution sur la précision par rapport au volume de RAM pour Envision?

Oui, absolument, bien que ce ne soit pas dans Envision lui-même. C’est un choix que nous avons fait dans la conception d’Envision. Mon approche concernant les Supply Chain Scientist est de les libérer des détails techniques de bas niveau. Les 4 kilo-octets d’Envision représentent beaucoup d’espace, permettant une représentation précise de votre situation de supply chain. Ainsi, l’approximation que vous perdez en termes de résolution et de précision est sans conséquence.

Il est vrai que, lorsqu’il s’agit de concevoir votre algorithme de compression, il existe de nombreux compromis à considérer. Par exemple, les compartiments très proches de zéro nécessitent une résolution parfaite. Si vous souhaitez obtenir la probabilité d’observer zéro unité de demande, vous ne voulez pas que votre approximation regroupe les compartiments pour une demande de zéro, une unité et deux unités. Cependant, si vous examinez les compartiments pour la probabilité d’observer 1 000 unités de demande, regrouper 1 000 et 1 001 unités est probablement acceptable. Ainsi, il existe de nombreuses astuces pour développer un algorithme de compression qui corresponde réellement aux exigences de la supply chain. Cela est d’un ordre de grandeur bien plus simple comparé à ce qui se passe pour la compression d’images. Selon moi, un outil correctement conçu permettrait essentiellement d’abstraire le problème pour les [Supply Chain Scientist]. Ceci est trop bas niveau, et il n’est pas nécessaire de micro-optimiser dans la plupart des cas. Si vous êtes Walmart et que vous disposez non pas d'1 million de SKUs mais de plusieurs centaines de millions, alors la micro-optimisation pourrait avoir un sens. Toutefois, à moins de parler de supply chains extrêmement grandes, je pense que vous pouvez avoir quelque chose de suffisamment bon pour que la perte de performance due à l’optimisation incomplète soit principalement sans conséquence.

Question: Quelles sont les considérations pratiques à prendre en compte d’un point de vue supply chain lors de l’optimisation de ces paramètres?

En ce qui concerne la prévision probabiliste dans la supply chain, disposer d’une précision de plus d’une partie sur 100 000 est généralement sans conséquence, tout simplement parce que vous n’avez jamais suffisamment de données pour obtenir une précision dans l’estimation de vos probabilités plus granulaire qu’une partie sur 100 000.

Question: Quel secteur industriel bénéficie le plus de l’approche de prévision probabiliste?

La réponse courte est la suivante : plus vos schémas sont erratiques et irréguliers, plus les bénéfices sont importants. Si vous avez une demande intermittente, vous en tirez de grands avantages ; si votre demande est erratique, vous en bénéficiez largement ; si vos délais varient considérablement et que des chocs erratiques frappent vos supply chains, vous en bénéficiez le plus. À l’extrême opposé, prenons, par exemple, la supply chain de la distribution d’eau : la consommation d’eau est extrêmement régulière et ne présente presque jamais de gros chocs – seulement de micros chocs au maximum. C’est le genre de problème qui ne bénéficie pas de l’approche probabiliste. L’idée est qu’il existe quelques situations où les prévisions ponctuelles classiques fournissent des estimations très précises. Si vous êtes dans une situation où vos prévisions pour tous vos produits affichent une erreur de moins de cinq pour cent à l’horizon, alors vous n’avez pas besoin de prévisions probabilistes ; vous êtes dans un contexte où une prévision réellement précise fonctionne. Cependant, si, comme de nombreuses entreprises, vous constatez une précision très faible dans vos prévisions, avec une divergence de 30 % ou plus, alors vous bénéficierez grandement de la prévision probabiliste. Au passage, lorsque je parle d’une erreur de prévision de 30 %, je fais toujours référence à la prévision la plus désagrégée. De nombreuses entreprises vous diront que leurs prévisions sont précises à 5 %, mais si vous tout agrégez, cela peut donner une perception très trompeuse de leur précision. La précision de vos prévisions n’a d’importance qu’au niveau le plus désagrégé, généralement au niveau des SKUs et sur une base journalière, car ce sont ces niveaux qui fondent vos décisions. Si, à ce niveau, vous pouvez obtenir des prévisions avec une précision de 5 %, alors vous n’avez pas besoin de prévisions probabilistes. Cependant, si vous observez des imprécisions à deux chiffres en pourcentage, alors vous bénéficierez énormément de la prévision probabiliste.

Question: Étant donné que les délais peuvent être saisonniers, décomposeriez-vous les prévisions de délai en plusieurs prévisions, chacune pour une saison distincte, afin d’éviter une distribution multimodale?

C’est une bonne question. L’idée ici est que vous construiriez typiquement un modèle paramétrique pour vos délais qui inclut un profil de saisonnalité. Traiter la saisonnalité pour les délais n’est fondamentalement pas très différent de traiter toute autre cyclicité, comme nous l’avons fait dans le cours précédent pour la demande. La façon typique n’est pas de construire plusieurs modèles, car comme vous l’avez correctement souligné, si vous avez plusieurs modèles, vous observerez toutes sortes de sauts bizarres en passant d’une modalité à l’autre. Il est généralement préférable d’avoir un seul modèle intégrant un profil de saisonnalité. Ce serait comme une décomposition paramétrique où vous disposez d’un vecteur qui vous donne l’effet hebdomadaire impactant le délai à une certaine semaine de l’année. Peut-être aurons-nous le temps, dans un cours ultérieur, de donner un exemple plus détaillé à ce sujet.

Question: La prévision probabiliste est-elle une bonne approche quand on veut prévoir une demande intermittente ?

Absolument. En fait, je pense que lorsqu’on a une demande intermittente, la prévision probabiliste n’est pas seulement une bonne méthode, mais la prévision ponctuelle classique devient carrément insensée. Avec la prévision classique, vous auriez généralement du mal à gérer tous ces zéros. Que faire de ces zéros ? Vous obtenez une valeur très faible et fractionnée, ce qui n’a pas vraiment de sens. Avec une demande intermittente, la question à laquelle vous voulez vraiment répondre est : est-ce que mes stocks sont suffisamment importants pour faire face à ces pics de demande qui surviennent de temps en temps ? Si vous utilisez une prévision moyenne, vous ne le saurez jamais.

Pour revenir à l’exemple de la librairie, si vous dites que dans une semaine donnée vous observez en moyenne une unité de demande par jour, combien de livres devez-vous conserver dans votre librairie pour offrir un taux de service élevé ? Supposons que la librairie soit approvisionnée chaque jour. Si les seules personnes que vous servez sont des étudiants, alors, avec en moyenne une unité de demande chaque jour, disposer de trois livres en stock se traduira par un taux de service très élevé. Cependant, si de temps à autre un professeur vient et demande 20 livres d’un coup, alors votre taux de service, avec seulement trois livres en magasin, sera épouvantable car vous ne pourrez jamais satisfaire la demande des professeurs. C’est typiquement le cas avec une demande intermittente – il ne s’agit pas seulement du fait que la demande est intermittente, mais aussi que certains pics de demande peuvent varier considérablement en termes d’ampleur. C’est là que la prévision probabiliste brille vraiment, car elle peut capturer la structure fine de la demande au lieu de la regrouper en moyennes qui font perdre tous ces détails.

Question: Si nous remplaçons le délai par une distribution, le pic représenté par une courbe en cloche lisse sur la première diapositive du générateur sera-t-il toujours présent ?

Dans une certaine mesure, plus vous introduisez d’aléa, plus les choses ont tendance à se disperser. Sur la première diapositive concernant le générateur, nous devrions exécuter l’expérience avec divers réglages pour voir ce que cela donne. L’idée est que lorsque nous voulons remplacer le délai par une distribution, c’est parce que nous avons une compréhension du problème qui nous indique que le délai varie. Si nous faisons une confiance absolue à notre fournisseur et qu’il a toujours été incroyablement fiable, alors il est parfaitement acceptable de dire que l’ETA (heure estimée d’arrivée) est ce qu’il est et constitue une estimation quasi parfaite de la réalité. Cependant, si nous avons constaté par le passé que les fournisseurs étaient parfois erratiques ou ne respectaient pas les délais, il est alors préférable de remplacer le délai par une distribution.

Introduire une distribution pour remplacer le délai ne lisse pas nécessairement les résultats finaux ; cela dépend de ce que vous observez. Par exemple, si vous considérez le cas le plus extrême de sur-stockage, un délai variable peut même exacerber le risque de stocks morts. Pourquoi cela ? Si vous avez un produit très saisonnier et un délai variable, et que le produit arrive après la fin de la saison, vous vous retrouvez avec un produit hors saison, ce qui magnifie le risque d’avoir des stocks morts à la fin de la saison. C’est donc délicat. Le fait de transformer une variable en son équivalent probabiliste ne lisse pas naturellement ce que vous allez observer ; parfois, cela peut même rendre la distribution plus pointue. La réponse est donc : ça dépend.

Excellent, je pense que c’est tout pour aujourd’hui. À la prochaine.