Continuous Ranked Probability Score (CRPS)

learn menu
Originariamente scritto da Joannes Vermorel, giugno 2016.
Aggiornato da Alexey Tikhonov, maggio 2024.

Le previsioni probabilistiche assegnano una probabilità a ogni possibile futuro. Tuttavia, tutte le previsioni probabilistiche non sono altrettanto accurate e sono necessarie metriche per valutare l’accuratezza rispettiva di diverse previsioni probabilistiche. Semplici metriche di accuratezza come MAE (Mean Absolute Error) o MAPE (Mean Absolute Percentage Error) non sono direttamente applicabili alle previsioni probabilistiche. Il Continuous Ranked Probability Score (CRPS) generalizza il MAE al caso delle previsioni probabilistiche. Insieme all’entropia incrociata, il CPRS è una delle metriche di accuratezza più utilizzate in cui sono coinvolte previsioni probabilistiche.

Panoramica

Il CRPS viene spesso utilizzato per valutare l’accuratezza rispettiva di due modelli di previsione probabilistica. In particolare, questa metrica può essere combinata con un processo di backtesting al fine di stabilizzare la valutazione dell’accuratezza sfruttando multiple misurazioni sullo stesso set di dati.

Questa metrica differisce notevolmente da metriche più semplici come il MAE a causa della sua espressione asimmetrica: mentre le previsioni sono probabilistiche, le osservazioni sono deterministiche. A differenza della funzione di perdita pinball, il CPRS non si concentra su un punto specifico della distribuzione di probabilità, ma considera l’intera distribuzione delle previsioni.

Definizione formale

Sia $${X}$$ una variabile casuale.

Sia $${F}$$ la funzione di distribuzione cumulativa (CDF) di $${X}$$, tale che $${F(y)=\mathbf{P}\left[X \leq y\right]}$$.

Sia $${x}$$ l’osservazione e $${F}$$ la CDF associata a una previsione probabilistica empirica.

Il CRPS tra $${x}$$ e $${F}$$ è definito come:

$$\qquad \qquad \qquad \qquad{CRPS(F, x) = \int_{-\infty}^{\infty}\Big(F(y)- 𝟙(y - x)\Big)^2dy} \qquad \qquad \qquad \qquad \qquad \qquad \tag{1}$$

dove $${𝟙}$$ è la funzione gradino di Heaviside e indica una funzione gradino lungo la retta reale che assume:

  • il valore di 1 se l’argomento reale è positivo o zero,
  • il valore di 0 altrimenti.

Il CRPS è espresso nella stessa unità della variabile osservata (ad esempio, se la domanda di un prodotto è stata prevista in unità, il CRPS sarà espresso anche in unità).

Il CRPS generalizza l’errore assoluto medio (MAE). Infatti, si riduce al MAE se la previsione è deterministica. Questo punto è illustrato nel grafico D di seguito.

Proprietà note

Gneiting e Raftery (2004) mostrano che il continuous ranked probability score può essere scritto in modo equivalente come:

$$\qquad \qquad \qquad \qquad {CRPS(F,x) = \mathbf{E}\Big[|X-x|\Big]-\frac{1}{2}\mathbf{E}\Big[|X-X^*|\Big]} \qquad \qquad \qquad \qquad \qquad \qquad \tag{2}$$

dove

  • $${X}$$ e $${X^*}$$ sono copie indipendenti di una variabile casuale lineare,
  • $${X}$$ è la variabile casuale associata alla funzione di distribuzione cumulativa $${F}$$,
  • $${\mathbf{E}[X]}$$ è il valore atteso di $${X}$$.

Valutazione numerica

Da un punto di vista numerico, un modo semplice per calcolare il CPRS consiste nel suddividere l’integrale originale in due integrali su confini ben scelti per semplificare la funzione gradino di Heaviside, ottenendo:

$$\qquad \qquad \qquad \qquad{CRPS(F, x) = \int_{-\infty}^x F(y)^2dy + \int_x^{\infty}\Big(F(y)- 1\Big)^2dy} \qquad \qquad \qquad \qquad \qquad \tag{3}$$

In pratica, poiché $$F$$ è una distribuzione empirica ottenuta attraverso un modello di previsione, la corrispondente variabile casuale $${X}$$ ha un supporto compatto, il che significa che ci sono solo un numero finito di punti in cui $${\mathbf{P}[X = x] \gt 0}$$. Inoltre, tutti i valori di $$x$$ sono numeri discreti. Pertanto, gli integrali possono essere trasformati in somme finite discrete come illustrato dalla formula seguente e dal grafico B nella sezione successiva.

$$\qquad \qquad \qquad \qquad{CRPS(F, x) = \sum_{k=0}^x F(y_k)^2 + \sum_{x+1}^{n} (F(y_k) - 1)^2} \qquad \qquad \qquad \qquad \qquad \qquad \tag{4}$$

Nella formula (4) un indice $$n$$ indica l’ultimo elemento della coda destra di una distribuzione di probabilità (ad esempio, il valore di domanda più alto con probabilità non nulla).

Infine, poiché il calcolo del CRPS viene effettuato per un singolo punto nel tempo, per calcolare il CRPS su un determinato periodo di valutazione di interesse (ad esempio, per la finestra di responsabilità, che è la somma del tempo di approvvigionamento del fornitore e del periodo di riordino) dovremmo calcolare una media dei valori di CRPS corrispondenti calcolati per quel periodo.

$$\qquad \qquad \qquad \qquad \qquad \qquad {CRPS = \frac{1}{T} \sum_{t=1}^{T} CRPS_t} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \tag{5}$$

Intuizione visiva

Per illustrare il calcolo del CRPS, considera il seguente esempio (consulta i grafici qui sotto):

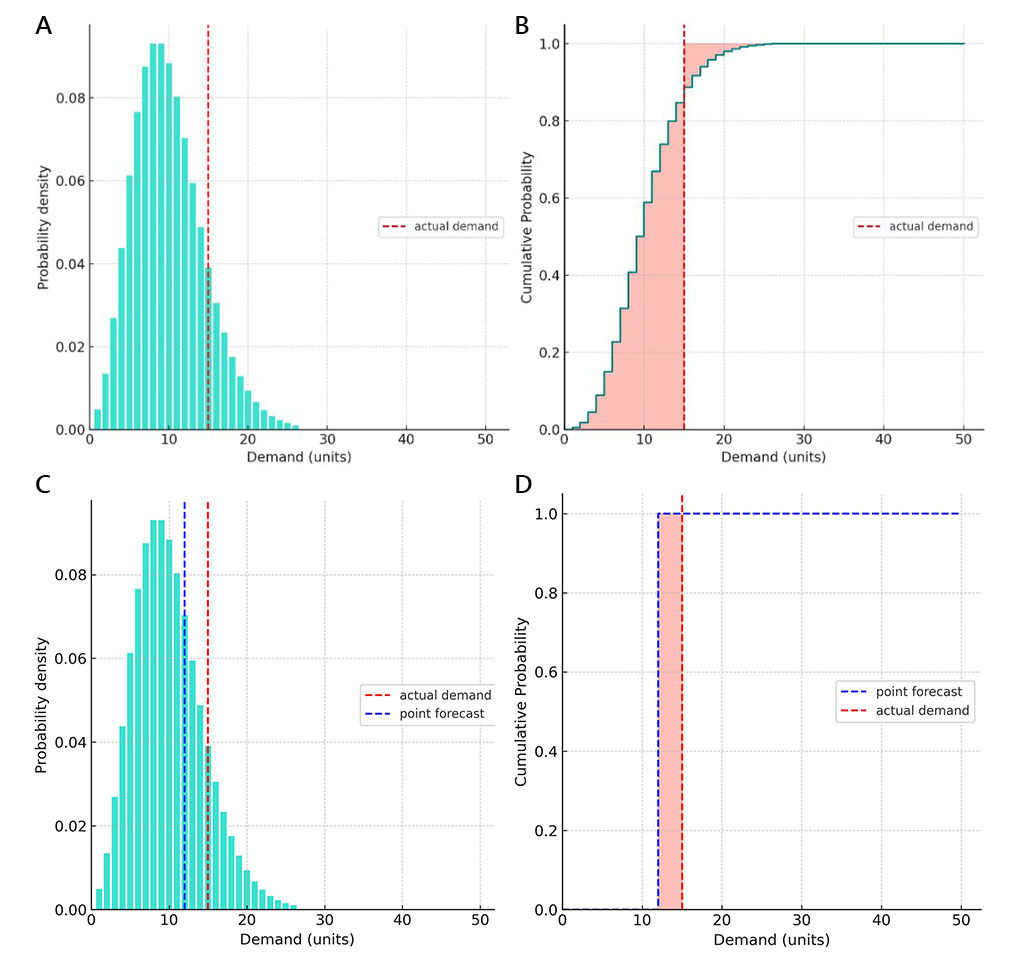
A: Inizialmente, abbiamo costruito una previsione di domanda probabilistica utilizzando una distribuzione binomiale negativa e troncando le code con probabilità inferiori allo 0,1% (che rappresentano eventi estremamente improbabili, come quelli che si verificano una volta ogni tre anni circa). I valori di domanda previsti con probabilità non nulla si estendevano nell’intervallo da 1 a 26 unità. Successivamente, si è scoperto che la domanda effettiva era di 15 unità (come indicato dalla linea tratteggiata rossa verticale).

B: Abbiamo calcolato il CRPS secondo la quarta formula sopra (vedi “Valutazione numerica”). Il valore di CRPS risultante rappresenta la somma di due aree riempite con il colore rosso chiaro.

C: Stesso grafico del grafico A, ma con una previsione puntuale aggiunta per confronto.

D: Il calcolo del CRPS applicato alla previsione puntuale dimostra che quando il CRPS viene applicato a una previsione puntuale, il risultato è una misura di accuratezza MAE. Infatti, le previsioni puntuali sono forme banali di previsioni probabilistiche in cui assegniamo implicitamente una probabilità del 100% a un singolo valore. Quindi, un grafico di probabilità cumulativa per il CRPS sarà rappresentato da due funzioni a gradino: una per le previsioni puntuali e una per la domanda effettiva. Ciò significa che a seconda delle posizioni relative della previsione puntuale rispetto al valore effettivo, una delle due somme nella formula del CRPS (4) diventerà zero: la prima somma per le sovrastime e la seconda somma per le sottostime.

Un grafico che illustra la previsione probabilistica e la metrica CRPS per valutarne l'accuratezza.
A: Previsione probabilistica. B: CRPS. C: Previsione probabilistica vs. previsione puntuale. D: Il CRPS della previsione puntuale è MAE.

Per l’esempio fornito attraverso questi 4 grafici, i valori di CRPS risultanti per la previsione probabilistica e per la previsione puntuale sono rispettivamente 3,32 e 3. Guardando i numeri, si potrebbe concludere che la previsione puntuale è più accurata perché la sua metrica di accuratezza è più piccola (migliore) rispetto a quella della previsione probabilistica. Tuttavia, questa conclusione è errata.

Nell’esempio sopra abbiamo considerato solo un valore di domanda effettiva, tuttavia quando la previsione probabilistica viene appresa utilizzando dati storici, le probabilità vengono regolate in base alle frequenze di occorrenza dei valori di domanda rispettivi (considerando i valori disponibili nel dataset di apprendimento). Se vengono scelti in modo appropriato, il valore medio di CRPS per il dataset di test sarà confrontabile con quello per il dataset di addestramento/validazione poiché la previsione rappresenterà adeguatamente le frequenze di occorrenza dei diversi valori di domanda nei dati di test.

Il grafico sottostante dimostra la superiorità delle previsioni probabilistiche rispetto alle previsioni puntuali.

Un grafico che illustra come CRPS cambia a seconda dei valori effettivi sia per le previsioni probabilistiche che per le previsioni puntuali.

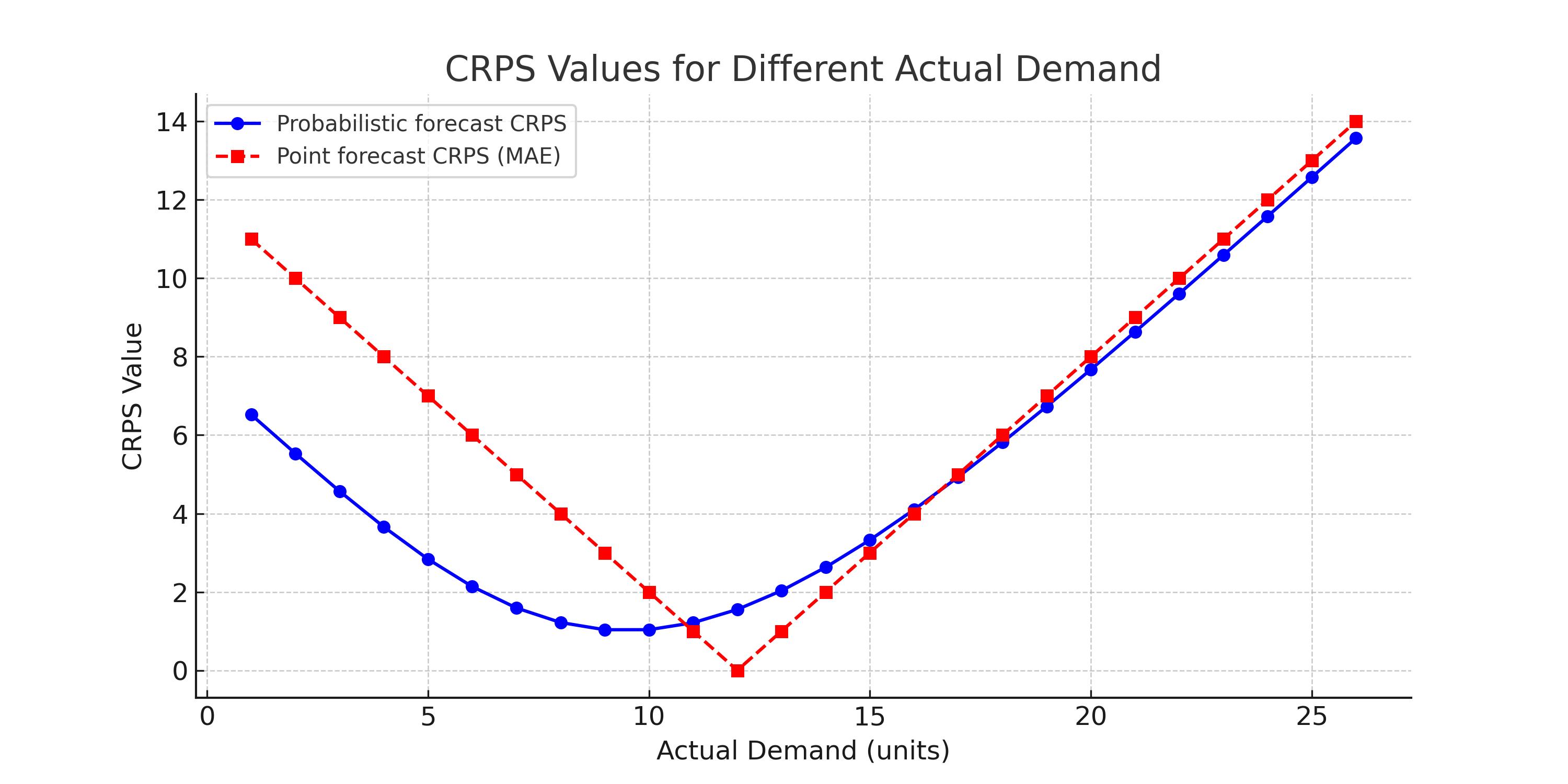
Notare come CRPS cambi in modo fluido a seconda dei diversi valori effettivi. Inoltre, notare che, a parte una piccola regione (dove la previsione puntuale è molto vicina all’effettiva), in tutte le altre aree il CRPS per le previsioni probabilistiche è inferiore a quello della previsione puntuale.

Se avessimo più previsioni puntuali diverse, questa osservazione sarebbe comunque valida. Bisognerebbe spostare mentalmente la curva rossa a sinistra o a destra a seconda della previsione puntuale, ma la superiorità della previsione probabilistica sarebbe comunque valida.

Riferimenti

Gneiting, T. e Raftery, A. E. (2004). Strictly proper scoring rules, prediction, and estimation. Technical Report no. 463, Department of Statistics, University of Washington, Seattle, Washington, USA.