不足と在庫、予測の精度が重要
需要予測は在庫最適化の基礎です。しかし、以下の間の正確な関係は:
は時に若干不明瞭です。そこで、状況を明確にしてみましょう.
不足は費用がかかる: 顧客の満足度が低下し、再来店の可能性が下がり、顧客獲得に投じた資金が無駄になり、間接的な売上も失われる可能性があります, …
しかし在庫コストも費用がかかります: 在庫が増えれば運転資金が多く必要となり、製品の陳腐化や倉庫費用が増加します;過剰在庫は広告費増加や販売単価の低下を招きます, …
したがって、顧客サービスは在庫量と品切れの量との間の財務的トレードオフとなります.
ここでは小売業の状況を前提としていますが、ほぼ同様の論理は製造業にも当てはまります.
現時点では、予測精度がどのように影響するのかはまだ不明です。特に、一部の企業では、そもそも予測が作成されていないように見えるかもしれません。例としては、単にmin-maxの再発注ポリシーを実施しており、需要予測が行われていない場合などです.
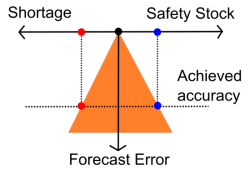
実際、会社内で誰も明示的に需要予測を行っていなくても、在庫は暗黙のうちに需要予測精度を持っているのです(上記の図では、制約を表すオレンジの三角形となっています)。実際、少々複雑ではあるものの、stock-keeping-unit-sku-定義における安全在庫水準と品切れ頻度をもって暗黙の予測精度を算出することが可能です.
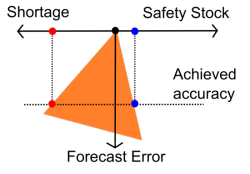
取引のバランス調整を、サービスレベル側に有利にしたとしても、在庫の削減側に有利にしたとしても、結果的に一方のコストが別のコストに置き換わるだけで、暗黙の予測精度が向上するわけではありません(右側の図では、制約が削減されるのではなく回転しています)。仮に需要予測がプロセスによって隠されていたとしても、その予測が誤っている場合、企業が財務的損失を被るのを防ぐことはできません.
もし在庫ポリシーに対する分析が十分であれば、不足と在庫のトレードオフを調整してももたらされる改善効果は僅かなものと予想されます(しかし、マージンが薄い場合には、依然として大きな節約につながる可能性があります).
等式の両面を改善するためには、より良い需要予測が必要です.
左側のグラフィックに、精度向上の影響が示されています。以前の状況と比較すると、予測精度の向上により、品切れ頻度と安全在庫量の両方を削減できることがわかります.
理論上、需要予測誤差を1%(相対値)削減することで、品切れ頻度を1%(相対値)削減するか、あるいは安全在庫量を1%(相対値)削減できると概ね述べています.
実際には, 追加精度によってもたらされる改善を完全に活用するには、たとえば自社サプライヤーが提供するサービスレベルのような障壁が存在するかもしれません。しかし保守的な見方をすれば、1%の追加精度は0.5%の品切れ削減または0.5%の安全在庫削減につながると推定できます.
その後、改善された精度を維持しながら、不足と在庫のトレードオフを再調整することが可能です.
読者コメント (6)
こんにちは、Benhard さん, 多くの安全在庫計算式は需要予測の分散に依存していますが、この値を算出するのが難しいため、一般的な経験則として、需要予測の分散を過去の実績データの分散で置き換える方法が用いられます。しかし、これはあくまで近似です. したがって、需要予測誤差を安全在庫計算に組み込みたい場合は、過去の分散に用いる「sigma」係数を、需要予測そのものの期待分散に置き換えてください. お役に立てば幸いです。
Joannes Vermorel (7 years ago)
こんにちは、Joannes さん, この記事は非常に興味深いと感じています。私は需要履歴ではなく需要予測に基づく在庫ポリシーの策定に取り組んでいます。ほとんどのウェブサイトでは、過去データの分散を基に在庫ポリシーを決定する方法が紹介されています。では、どうすれば需要予測誤差を安全在庫の計算式に組み込むことができるのでしょうか. 私の質問が上記の話題から逸れている場合は申し訳ありません。どんな助言でもありがたいです. ありがとう、Jo. ben
Benhard Adolf (7 years ago)
実際のところ、重要なのは三角形そのものではなく、その両側の辺(右と左)です。直感的には、主要な角度は変えられない定数であるため、片方の辺を動かせばもう片方も動いてしまいます。形状は三角形のように見えますが、実際には2つの辺と1つの角度だけが重要です。
Joannes Vermorel (8 years ago)
親愛なる Joannes さん, あなたの説明は非常に明快ですが、オレンジの三角形が理解できません。これは制約を表しています。しかし、図ではそれがよく分かりません。もう少し説明を加えていただけますか。ありがとうございます
Piet Buyck (8 years ago)
こんにちは Achyut さん、古典的な安全在庫モデルでは、通常、需要が正規分布(ガウス分布)に従うと仮定します。正規分布は平均と分散という2つのパラメータで定義されます。特定のサービスレベルに対して、安全在庫(すなわち平均需要を上回る追加在庫)の量は分散に線形に比例します。したがって、この理想モデルでは、分散(すなわち需要予測誤差)を1%削減すれば、安全在庫も1%削減されます。その後、同じ安全在庫量を維持しながら品切れ頻度を削減するという点はさらに複雑であり、これだけでもブログ記事を書く必要があるでしょう。時間が取れたときに、また改めて取り上げたいと思います。
Joannes Vermorel (8 years ago)
こんにちは、Joannes さん, この記事はとても有用です。ただ、本記事で述べられている点の一つについて、もう少し明確な説明が欲しいです。あなたは「理論上、需要予測誤差を1%(相対値)削減することで、品切れ頻度を1%(相対値)削減するか、安全在庫量を1%(相対値)削減できる」と述べましたが、その根拠となる概念について詳しく説明していただけますか?より良い需要予測が在庫レベルを削減することになるのは理解していますが、その効果を定量化するのが難しいと感じています. 事前に感謝します
Achyut Koushik A (8 years ago)


