00:18 はじめに
02:18 背景
12:08 なぜ最適化するのか? 1/2 Holt-Wintersによる予測
17:32 なぜ最適化するのか? 2/2 - 車両経路問題
20:49 これまでの経緯
22:21 補助科学(復習)
23:45 問題と解決策(復習)
27:12 数学的最適化
28:09 凸性
34:42 確率性
42:10 多目的
46:01 ソルバー設計
50:46 ディープ(ラーニング)レッスン
01:10:35 数学的最適化
01:10:58 “本物の"プログラミング
01:12:40 局所探索
01:19:10 確率的勾配降下法
01:26:09 自動微分
01:31:54 微分可能プログラミング (2018年頃)
01:35:36 結論
01:37:44 今後の講義と聴衆からの質問
説明
数学的最適化 は数学的関数を最小化するプロセスです。近代のほとんどすべての統計学的学習手法 ― すなわち、供給チェーンの視点 を採用した場合の予測も ― は、その核心において数学的最適化に依拠しています。さらに、一度予測が確立されると、最も有利な意思決定の特定も根本的には数学的最適化に依存します。サプライチェーンの問題はしばしば多数の変数を含み、通常は確率的な性質を持っています。数学的最適化は現代のサプライチェーン実践の礎となるものです。
完全なトランスクリプト

このサプライチェーン講義シリーズへようこそ。私はジョアンネス・ヴェルモレルです。本日は「サプライチェーンのための数学的最適化」について発表いたします。数学的最適化とは、与えられた問題に対して最良の解を見出すための、明確に定義され、形式化された計算可能な手法です。すべての予測問題は数学的最適化問題と見なすことができます。また、サプライチェーン内外のすべての意思決定状況も数学的最適化問題とみなせます。実際、数学的最適化の視点は現代の世界観に深く根ざしており、与えられた狭い枠の外で「最適化する」という動詞を定義することは非常に困難になっています。
さて、数学的最適化に関する科学文献は膨大であり、それを支えるソフトウェアエコシステムもまた広範です。残念ながら、その多くはサプライチェーンにおいてはあまり有用でもなく、関連性も高いとは言えません。この講義の目的は二重です。第一に、サプライチェーンの観点から価値があり実用的な成果を得るために、数学的最適化にどのように取り組むかを理解すること。そして第二に、この広大な分野の中から最も価値ある要素を見出すことです。

数学的最適化の形式的定義はシンプルです。通常、損失関数と呼ばれる関数を考え、この関数は実数値を返し、単に数値を生成します。求めるべきは、その損失関数を最小化する最良の値を示す入力(X0)の特定です。これが典型的な数学的最適化のパラダイムであり、一見すると単純ですが、この一般的な視点についてはさまざまな議論が可能です。
応用数学的最適化の観点から見ると、この分野は主にオペレーショナル・リサーチという名称の下で発展しました。具体的には、20世紀の1940年代から1970年代後半にかけて行われた古典的オペレーショナル・リサーチを指します。古典的オペレーショナル・リサーチは数学的最適化と比較して実際のビジネス問題に深く関心を寄せていました。一方で数学的最適化は最適化問題の一般的な形態に注目し、問題がビジネス上の重要性を持つかどうかにはあまり関心がありません。実際、古典的オペレーショナル・リサーチは本質的には最適化を行っていましたが、あらゆる問題ではなく、ビジネス上重要と認識された問題にのみ焦点を当てていました。
興味深いことに、我々はオペレーショナル・リサーチから数学的最適化への移行を、20世紀初頭に経済活動の将来レベルの一般的な予測に関心を持って登場した予測分野から、すなわち時系列予測から機械学習への移行とほぼ同じ方法で経験しました。この分野は、より広範な問題に対する予測に注目する機械学習によって本質的に取って代わられました。つまり、予測から機械学習への移行と同様に、オペレーショナル・リサーチから数学的最適化への移行もおおまかに同じ変遷をたどったと言えます。さて、古典的オペレーショナル・リサーチの時代が70年代後半まで続いたと言ったとき、私は非常に具体的な日付を念頭に置いていました。1979年2月、ラッセル・アッコフは「The Future of Operational Research is Past」という衝撃的な論文を発表しました。この論文を理解するためには、ラッセル・アッコフがオペレーショナル・リサーチの創始者の一人であることを理解する必要があります。
彼がこの論文を発表したとき、彼はもはや若者ではなく60歳でした。アッコフは1919年生まれで、彼のキャリアのほとんどをオペレーショナル・リサーチの仕事に費やしてきました。論文発表時、彼はオペレーショナル・リサーチが失敗に終わったと基本的に主張しました。結果が出なかっただけでなく、その業界への関心も低下しており、90年代末には20年前と比べてこの分野への関心が薄れていました。
興味深いのは、その原因が当時のコンピューターが今日のものよりも遥かに性能が低かったという事実に全く起因しない点です。この問題は処理能力の制限に関係がありません。70年代末の当時、コンピューターは現代に比べ非常に控えめな性能でしたが、それでも合理的な時間内に何百万もの算術演算を行うことができました。つまり、問題は処理能力の制限に起因するものではないのです。
ちなみに、この論文は非常に読み応えがあります。ぜひ皆さんにもご一読いただきたいと思います。お気に入りの検索エンジンで容易に見つけることができるでしょう。この論文は非常に分かりやすく、よく書かれています。アッコフがこの論文で指摘した問題は40年経った今でも依然として強く響いており、多くの点で現代のサプライチェーンを悩ませる問題を予見していると言えます。
では、問題は何でしょうか? 問題は、ある関数を取り最適化するというこのパラダイムにおいて、最適化プロセスが良い、あるいは最適な解を見出すと証明できたとしても、実際に最適化している損失関数がビジネスにとっていかに有意義であるかをどう証明するかにあります。つまり、ある問題や関数を最適化できると言った場合、その最適化対象が実際には幻想に過ぎない可能性があるということです。最適化しようとしている対象が、実際に最適化すべきビジネスの現実とは全く関係がないとしたらどうなるのでしょうか?
ここに問題の核心があり、初期の試みがほぼすべて失敗した理由にもなっています。なぜなら、ビジネスの利益を表すはずの何らかの数学的表現を作り出しても、結果として得られるのは文字通り数学的な幻想に過ぎなかったからです。これこそがラッセル・アッコフがこの論文で指摘していることであり、彼は長い間この手法を実践してきた結果、本質的には何の成果も生み出していないと認識しているのです。彼は自身の論文で、この分野は失敗に終わったという見解を示し、診断を行いましたが、解決策についてはほとんど示しませんでした。非常に興味深いことに、創始者の一人であり尊敬され認知された研究者が、この研究分野全体が行き詰まりであると言っているのです。彼は残りの長い人生を、ビジネス最適化における定量的視点から完全に定性的視点へと移行するために費やすことになりました。彼は人生の最後の30年を定性的手法に注力し、その転換点以降の後半生でも非常に興味深い業績を残すことになるのです。
さて、この講義シリーズにおいては、ラッセル・アッコフがオペレーショナル・リサーチについて提起した問題は今日でも非常に有効ですが、我々はどのように対処すべきでしょうか。実際、私は既にアッコフが指摘した最大の問題点に取り組み始めており、当時彼やその仲間たちが解決策を持っていなかったように、問題の診断はできても解決策は示されていませんでした。この講義シリーズで私が提案する解決策は、オペレーショナル・リサーチの視点に内在する根深い方法論的問題に対する、方法論的なアプローチなのです。
私が提案する方法は基本的に二つに分かれます。一方はサプライチェーン担当者へのアプローチ、もう一方は数学的最適化を補完する実験的最適化と呼ばれる手法です。また、ビジネス上の関心や関連性を強調するオペレーショナル・リサーチとは異なり、今日私が問題に取り組む方法はオペレーショナル・リサーチの視点ではなく、数学的最適化の視点からアプローチしています。私は、サプライチェーンにおける数学的最適化には本質的な根本性はなく、あくまで基礎的な関心事であり、目的そのものではなく手段であると述べています。これが違いの所在です。この点は非常に単純かもしれませんが、実際に予測レベルの成果を達成する上では極めて重要なのです。

さて、そもそもなぜ最適化を行いたいのでしょうか? ほとんどの予測アルゴリズムは、その核心に数学的最適化問題を抱えています。画面に表示されているのは、ごく古典的な乗法的 Holt-Winters 時系列予測アルゴリズムです。このアルゴリズムは主に歴史的意義を持つものであり、現代のサプライチェーンで実際に利用することは推奨しません。しかし、シンプルさのために、これは非常に単純なパラメトリック手法であり、画面全体に収まるほど簡潔です。冗長ではありません。
画面に表示されるすべての変数は単なる数値であり、ベクトルは含まれていません。基本的に、Y(t) があなたの推定値、すなわち時系列予測です。この画面ではH期間先を予測しており、Hは予測の地平線のようなものです。そして、実際には時系列であるY(t)に取り組んでいると考えることができます。これを週次あるいは月次の集計売上データと考えることも可能です。このモデルは基本的に3つの構成要素からなります。Ltはレベル(各期間ごとに一つのレベルがあります)、Btはトレンド、そしてStは季節成分です。Holt-Wintersモデルを学ぶ場合、パラメータはalpha、beta、gammaの3つがあります。これらのパラメータは基本的に0から1の間の数値です。つまり、3つのパラメータすべてが0から1の数値であり、Holt-Wintersアルゴリズムを適用するということは、これら3つのパラメータの適切な値を特定することを意味するのです。アイデアは、これらのパラメータ(alpha、beta、gamma)が、あなたが予測のために指定した誤差を最小化する場合に最適となるということです。この画面では、非常に古典的な平均二乗誤差が示されています。
数学的最適化の要点は、alpha、beta、gammaの適切なパラメータ値を特定する手法を考案することにあります。では、何ができるでしょうか? 最も簡単で単純な方法はグリッドサーチのような方法です。グリッドサーチはすべての値を探索するという考え方に基づいています。これらは小数であるため、値は無限に存在するので、実際には解像度、たとえば0.1刻みを採用し、0.1ずつ増加させて探索するのです。0から1の範囲に3つの変数があるため、0.1刻みでは約1,000回の反復で最適な値を見つけることになります。
しかし、この解像度はかなり粗いです。0.1刻みではパラメータのスケールに対して約10%の解像度しか得られません。そこで、0.01刻みにすればはるかに良く、1%の解像度が得られます。しかし、その場合、組み合わせの数は急激に増加します。1,000通りの組み合わせが100万通りに増え、これがグリッドサーチの問題点、すなわち非常に短時間で組み合わせの壁に突き当たり、選択肢が膨大になるという問題です。
数学的最適化とは、与えられた計算資源を投入して、より効率的な成果(コストパフォーマンス)を得るためのアルゴリズムを考案することです。単なる総当たり探索よりもはるかに優れた解が得られるでしょうか? 答えは、はい、絶対に可能です。
では、より少ない計算資源でより良い解を得るためには何ができるでしょうか? まず、何らかの勾配法を用いることが考えられます。Holt-Wintersの全式は、極小の例外的な除算を除いて完全に微分可能です。つまり、この全式は損失関数を含め完全に微分可能であり、勾配を利用して探索を導くというアプローチが可能です。
もう一つのアプローチとして、実際のサプライチェーンにおいては膨大な時系列データが存在するかもしれません。ですから、各時系列を個別に扱う代わりに、最初の1,000の時系列についてグリッドサーチを行い、投資後にα、β、γの良い組み合わせを特定し、残りの時系列についてはこの候補リストから最適な解を選ぶという方法が考えられます。
ご覧のとおり、単なるグリッドサーチアプローチを超えて大幅に改善するための単純なアイデアは数多く存在し、数学的最適化の本質やあらゆる意思決定問題も、通常は数学的最適化問題として捉えることができます。
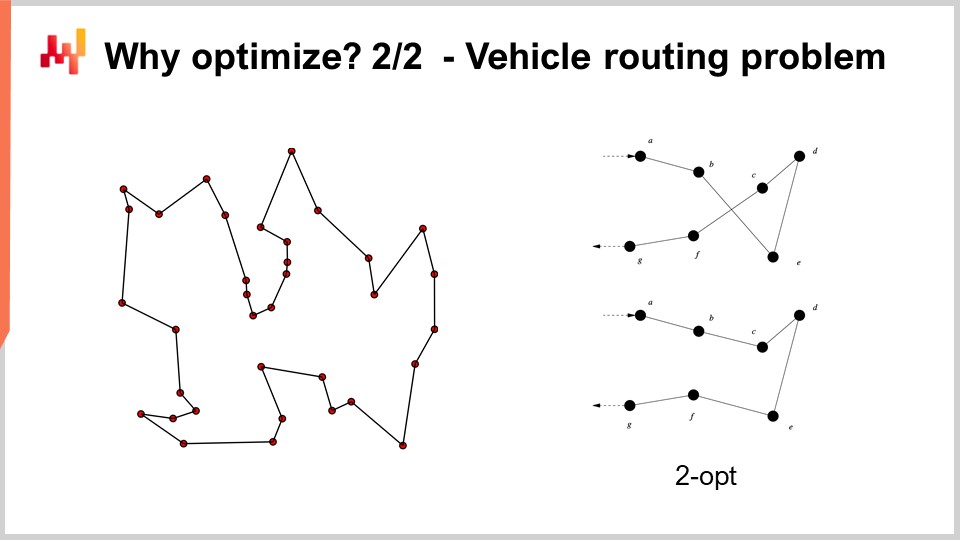
例えば、画面に表示されている車両ルーティング問題は数学的最適化問題とみなすことができます。これは、ポイントのリストを選ぶ問題です。問題の形式的な定式化は、そのバリエーションが多く、あまり有益な洞察をもたらさないため記載しませんでした。しかし、考え方としては、「ポイントがあり、各ポイントに単なるスコアとしての疑似ランクを割り当て、その疑似ランクで全てのポイントを昇順に並べれば、それがルートになる」という風に捉えることができます。アルゴリズムの目的は、最良のルートをもたらす疑似ランクの値を特定することです。
さて、この問題では、グリッドサーチがまったく選択肢にすらならないことが分かります。数十のポイントがあり、すべての組み合わせを試すとその数はあまりにも膨大になってしまいます。また、勾配法も役立たないでしょう。少なくとも、その有用性が明確ではなく、問題自体が非常に離散的であるため、この種の問題に対する明確な勾配降下法は存在しません。
しかし、この種の問題に取り組むためには、文献で明らかにされた非常に強力なヒューリスティックが存在することが判明しています。例えば、1958年にCroesによって発表されたtwo-optヒューリスティックは、非常にシンプルな手法を提供します。まずランダムなルートから始め、そのルートが自己交差するたびに、その交差を取り除くために順列操作を行います。つまり、ランダムなルートから始め、最初に観察された交差を取り除く操作を行い、その後そのプロセスを繰り返します。交差がなくなるまでヒューリスティックを繰り返すと、この非常にシンプルな手法から実際に非常に良い解が得られるのです。真の数学的意味で最適解ではないかもしれません―必ずしも完璧な解ではありませんが、比較的少ない計算資源で非常に良い解を得ることができます。
しかし、two-optヒューリスティックの問題点は、非常に優れた手法である一方で、この特定の問題に極めて特化している点にあります。数学的最適化において真に興味深いのは、特定の一つの問題にしか使えないヒューリスティックではなく、広範な問題群に適用可能な手法を見出すことです。つまり、非常に一般的な手法が求められるのです。
さて、これまでの講義シリーズの流れを振り返ります。本講義は一連の講義の一部であり、現在の章はサプライチェーンの補助科学に捧げられています。第一章では、サプライチェーンを学問分野としても実践としてもどう捉えるかについての私見を提示しました。第二章は方法論に特化し、特に本講義に最も関連する実験的最適化という方法論を紹介しました。これは、数十年前にRussell Ackoffが指摘した非常に重要な問題に対処する鍵となるものです。第三章は完全にサプライチェーンの人材に捧げられています。本講義では、解と問題を混同するのではなく、解決すべき問題そのものを特定することに焦点を当てています。そして第四章では、サプライチェーンのすべての補助科学を検証します。ハードウェアという最も低いレベルから始まり、アルゴリズム、そして数学的最適化へと段階的に進んでいく流れがあります。このシリーズ全体で、抽象化のレベルを順次高めています。

補助科学を簡単に振り返ると、これらはサプライチェーン自体に対する新たな視点を提供します。現在の講義はサプライチェーンそのものについてではなく、むしろサプライチェーンの補助科学の一分野についてです。この視点は、古典的なオペレーショナルリサーチ―それ自体が目的とされる―と、目的の手段に過ぎない数学的最適化との間に大きな違いをもたらします。少なくともサプライチェーンに関しては、数学的最適化はビジネスの具体性を気にせず、数学的最適化とサプライチェーンの関係は、化学と医学の関係に似ています。現代の視点からは、優秀な医師になるために卓越した化学者である必要はありませんが、化学について全く知らないと主張する医師は疑わしく思われるでしょう。

数学的最適化は、問題が既知であることを前提としています。問題の妥当性を問うのではなく、与えられた問題に対して最適化を最大限に活用することに注力するのです。ある意味、それは顕微鏡のようなもので、非常に強力ですが焦点は極めて狭いのです。オペレーショナルリサーチの未来について議論に戻ると、もし顕微鏡の向きを誤れば、興味深いが最終的には無関係な知的課題に気を取られてしまう危険性があるのです。
だからこそ、数学的最適化は実験的最適化と併用される必要があるのです。前回の講義で扱った実験的最適化は、現実世界からのフィードバックを基に、問題そのもののより良いバージョンへと反復的に進化させるプロセスです。実験的最適化は、解ではなく問題を変異させるプロセスであり、反復を通じて良い問題へと収束させるのです。これが問題の核心であり、当時Russell Ackoffやその仲間たちが解決策を持たなかった理由です。彼らは与えられた問題を最適化するツールは持っていましたが、問題が良い状態になるまで変異させるツールは持っていなかったのです。象牙の塔内で記述できる数学的問題を、現実世界からのフィードバックなしで扱えば、それは幻想に過ぎません。実験的最適化プロセスを始める際の出発点はただの幻想であり、それを機能させるには現実世界からのフィードバックが必要です。要は、数学的最適化と実験的最適化を行き来しながら、各段階で数学的最適化ツールを用い、計算資源とエンジニアリング労力の両方を最小限に抑えながら、次の問題バージョンへと反復的に改善していくのです。

この講義では、まず数学的最適化の視点に対する理解を深めます。形式的な定義は一見単純ですが、サプライチェーンに実用的な関連性を持たせるためには注意すべき複雑な点も存在します。その後、サプライチェーンの視点から見た数学的最適化の最先端を担う二大クラスのソルバーについて探求していきます。
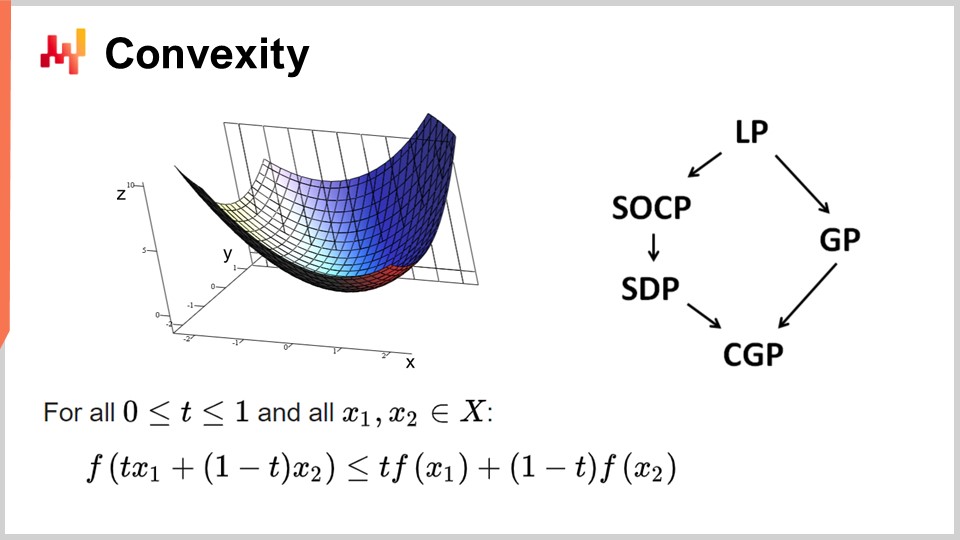
まず、凸性と数学的最適化の初期の研究について議論しましょう。オペレーショナルリサーチは当初、凸形状の損失関数に焦点を当てていました。ある関数が凸であるとは、特定の性質を満たすことを意味します。直感的には、関数上の任意の二点を直線で結んだとき、その直線が常に二点間の関数の値より上に位置する場合、その関数は凸であるといえます。
凸性は、真の数学的最適化―すなわち理論的な証明が可能な最適化―を実現するための鍵です。直感的には、凸関数を持つ場合、任意の点(候補解)において、周囲を見渡せば常に降下可能な方向が存在することを意味します。開始地点に関わらず降下でき、降下することは常に好ましい動きです。降下が不可能となるのは、本質的に最適点のみです。ここでは単純化していますが、解が一意でなかったり存在しない場合といった例外もあります。しかし、いくつかの例外を除けば、凸関数においてこれ以上最適化できないのは最適点だけです。それ以外では常に降下が可能であり、降下は良い選択です。
凸関数に関する研究は膨大であり、これまでにさまざまなプログラミングパラダイムが登場しました。LPは線形計画法を意味し、他には二次円錐計画法、幾何学的プログラミング(多項式を扱う)、半正定値計画法(正の固有値を持つ行列を対象とする)、および幾何学的円錐計画法などがあります。これらのフレームワークは、構造化された凸問題を扱うという共通点があり、損失関数だけでなく、適用可能な解を制限する制約条件においても凸性が保たれています。
これらのフレームワークは非常に高い関心を集め、膨大な科学文献が生み出されました。しかし、その印象的な名称にもかかわらず、これらのパラダイムは表現力に乏しいのです。単純な問題でさえ、これらのフレームワークの能力を超えてしまいます。例えば、1960年代の基本的な予測モデルであるホルト・ウィンタース法のパラメータ最適化は、これらのフレームワークが対応できる範囲を既に超えています。同様に、車両ルーティング問題や巡回セールスマン問題という単純な問題も、これらのフレームワークの限界を超えています。
だからこそ、冒頭で述べたように、膨大な文献が存在するにもかかわらず、実用性のあるものは非常に少ないのです。降下が不可能となるのは、本質的には最適点だけです。ここでは単純化していますが、解が一意でない場合や全く解が存在しない場合といった例外もあります。しかし、いくつかの例外を除けば、凸関数でこれ以上最適化できないのは最適点のみです。それ以外では常に降下が可能であり、降下は良い戦略です。
凸関数に関する研究は膨大であり、これまでにさまざまなプログラミングパラダイムが登場しました。LPは線形計画法を指し、他には二次円錐計画法、幾何学的プログラミング(多項式を扱う)、半正定値計画法(正の固有値を持つ行列を対象とする)、および幾何学的円錐計画法などがあります。これらのフレームワークはすべて、構造化された凸問題を扱うという共通点を持ち、損失関数だけでなく、適用可能な解を限定する制約においても凸性が保たれています。
これらのフレームワークは非常に高い関心を集め、膨大な学術文献が生み出されました。しかし、その印象的な名称にもかかわらず、これらのパラダイムは表現力に非常に乏しいのです。単純な問題でさえ、これらのフレームワークの能力を超えてしまいます。例えば、1960年代の基本的な予測モデルであるホルト・ウィンタース法のパラメータ最適化は、これらのフレームワークが対応できる範囲を既に超えています。同様に、車両ルーティング問題や巡回セールスマン問題のような簡単な問題も、これらのフレームワークの限界を超えています。
だからこそ、冒頭で述べたように、膨大な文献が存在するにもかかわらず、実用性はほとんどありません。その一因は、純粋な数学的最適化ソルバーに誤った関心が向けられていたことにあります。これらのソルバーは数学的観点からは非常に興味深く、数学的証明を生み出すことができますが、実際にはおもちゃの問題や架空の問題にしか適用できません。現実世界に適用すれば失敗し、過去数十年、この分野ではほとんど進展がありません。サプライチェーンに関しては、いくつかのニッチを除いて、これらのソルバーが役立つことはほとんどありません。

古典的なオペレーショナルリサーチの時代に完全に無視されていたもう一つの側面は、ランダム性です。ランダム性、すなわち確率的性質は、全く異なる2つの観点から極めて重要です。第一の観点は、ソルバー自体においてランダム性をどのように扱うかという点です。現代では、最先端のソルバーは内部で確率過程を広範に活用しており、これは完全に決定論的なプロセスを採用する場合とは一線を画しています。ここで述べているのは、数学的最適化技術を実装するソフトウェアの一部の内部動作のことです。
すべての最先端ソルバーが確率過程を広範に活用する理由は、現代のコンピュータハードウェアの仕組みに起因します。解を探索する際に、ランダム性の代わりに過去の試行結果を記憶すると、同じループに陥る可能性があります。記憶する必要があれば、その分メモリを消費してしまいます。大量のメモリアクセスが必要になるため、ランダム性を導入することは、ランダムなメモリアクセスの必要性を大幅に軽減する一つの方法となるのです。
プロセスを確率的にすることで、最適化すべき問題に対してこれまでテスト済みか未テストの解のデータベースを参照する必要がなくなります。多少ランダムに行いますが、完全にランダムというわけではありません。これは、ほぼすべての現代ソルバーにとって重要な要素です。確率的プロセスを採用すると、一見直感に反して、確率的なソルバーであっても結果はかなり決定論的になり得るのです。これを理解するには、一連のふるいの類推を考えてみてください。ふるいは本質的に物理的な確率過程であり、ランダムな動きを加えながら選別が行われます。プロセス自体は完全に確率的であっても、その結果は完全に決定論的で予測可能なのです。最終的には、根本的にランダムなプロセスであっても、ふるいの選別によって得られる結果は明確に予測できるものとなります。これが、よく設計された確率的ソルバーで実際に起こる現象であり、現代ソルバーの重要な要素の一つです。
ランダム性に関して直交するもう一つの側面は、問題自体が確率的であるという性質です。これは、古典的なオペレーショナルリサーチの時代にはほとんど見られなかった点であり、損失関数がノイズを含んでおり、その測定値がある程度のノイズを伴うという考えです。サプライチェーンにおいては、ほぼ常にこの状況が当てはまります。なぜなら、サプライチェーンでは意思決定を下すたびに、何らかの将来の事象を予測しているからです。もし何かを購入することを決めるなら、それは将来的にその商品が必要になると予測しているからです。未来は定まっていないため、未来についての洞察は得られても、その洞察は決して完璧ではありません。今すぐ製品を生産する決断をする場合も、将来的にその製品に需要が生じると期待しているからです。今日という意思決定の質は、将来の不確実な条件に依存しており、結果としてサプライチェーンにおけるどの意思決定も、制御不可能な将来条件に応じて変動する損失関数を伴います。このような将来の事象を扱うためのランダム性は解消不可能であり、私たちが根本的に確率的な問題に取り組んでいることを示しているのです。
しかし、古典的な数学的ソルバーに目を向けると、この側面が完全に欠落していることが分かり、これは大きな問題です。つまり、我々が直面する問題を理解すらできないソルバーの種類が存在するということです。なぜなら、興味のある問題、すなわち数学的最適化を適用したい問題は、確率的な性質を持っているからです。ここで言うのは、損失関数に含まれるノイズのことです。
確率的な問題がある場合、サンプリングを通してそれを決定論的な問題に変換できるという反論もあります。もしノイズのある損失関数を1万回評価すれば、ほぼ決定論的な損失関数を得ることができるでしょう。しかし、このアプローチは最適化プロセスに1万倍のオーバーヘッドを導入するため、非常に非効率的です。数学的最適化の観点は、限られた計算資源で最良の結果を得ることに焦点が当たっており、無限の計算資源を投入して問題を解決することではありません。たとえその資源がかなり多くても、我々は有限の計算資源で対処しなければならないのです。したがって、後にソルバーを検討する際には、決定論的なアプローチに頼るのではなく、確率的な問題を本来の形で捉えられるソルバーを持つことが最も重要であることを念頭に置く必要があります。
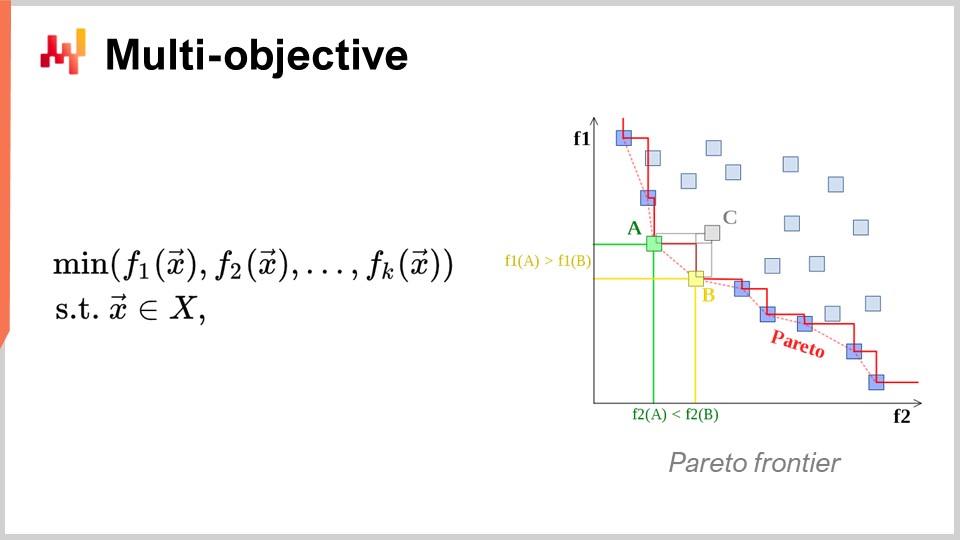
もう一つの極めて重要な観点は、多目的最適化です。数学的最適化問題を素朴に表現すると、損失関数は本質的に一つの値であり、最小化すべきものは一つであると言いました。しかし、もし値のベクトルがあり、全てのベクトル(f1、f2、f3 など)の辞書順で最も低い点を与える解を求める場合はどうでしょうか?
なぜこれがサプライチェーンの視点からも重要なのでしょうか? 実際、多目的の視点を採用すれば、すべての制約をひとつの専用の損失関数として表現することが可能になるからです。まず、制約違反の回数を数える関数を持つことができます。なぜサプライチェーンには制約が存在するのでしょうか? それは、あらゆる場所に制約があるからです。例えば、発注を行う場合、商品の到着時にそれを保管するための十分なスペースが倉庫にあることを確認しなければなりません。つまり、保管スペースや生産能力などの制約が存在します。各制約を個別に扱うソルバーを用いる代わりに、制約を一つの目的の一部として表現できるソルバーを使用する方が興味深いのです。単に制約違反の数を数え、それをゼロに最小化しようとするのです。
この考え方がサプライチェーンにとって非常に重要なのは、サプライチェーンが直面する最適化問題が、暗号パズルのような性質のものではないからです。つまり、解があればそれで良いというか、解からほんの少し外れれば何も得られないというような極端にタイトな組み合わせ問題ではありません。サプライチェーンでは、いわゆる実行可能解―すなわち全ての制約を満たす解―を得ることは通常、非常に容易です。制約を満たす解を一つ見つけること自体は大した労力ではありません。大きな難関は、制約を満たすすべての解の中から、ビジネスにとって最も有利なものを見つけ出すことにあるのです。ここが非常に困難な点です。制約違反がない解を見つけることはごく単純ですが、例えば携帯電話内部の部品配置など、工業デザインのための数学的最適化では、問題が非常に厳しい制約条件に縛られており、たった一つの制約を無視しても許されるような余裕はありません。それほど厳格な組み合わせ問題では、制約を最優先事項として扱わなければなりません。しかし、サプライチェーン問題の大部分においては、そこまでの厳格さは必要ないと私は考えます。したがって、多目的最適化に自然に対応できる技術が再び非常に重要になるのです。
さて、ソルバーの設計についてもう少し詳しく議論しましょう。非常に広範な問題群に対して解を生成するソフトウェアをどのように設計するかという高レベルの視点から、特に注目すべき設計上の側面が二つあります。まず一つ目は、ホワイトボックスかブラックボックスかという視点です。ブラックボックスの考え方では、任意のプログラムを処理できるため、損失関数も任意のプログラムでよいとし、中身は気にせず完全なブラックボックスとして扱います。必要なのは、「プログラムを評価して候補解の値を得る」ということだけです。一方、ホワイトボックスアプローチは、損失関数自体に観察可能で活用可能な構造がある点を強調します。つまり、損失関数の内部を確認できるのです。ちなみに、数スライド前に凸性について議論した際、あのモデルや純粋な数学的ソルバーは実際にホワイトボックスアプローチであり、問題の内部が見えるだけでなく、セミデフィニットプログラミングのように非常に狭い形状の厳格な構造を持っている極端な例でした。しかし、数学的枠組みほど厳格でなくても、ホワイトボックスの一部として、例えば勾配のような指標を利用することができるのです。損失関数の勾配は非常に重要で、たとえ凸問題でなくとも、単純な勾配降下法が良い結果を保証しない場合でも、どの方向に進むべきかを示してくれます。経験則として、ソルバーをホワイトボックス化できれば、ブラックボックスソルバーに比べて桁違いに高性能なソルバーが実現できるでしょう。
次に、オフラインソルバーとオンラインソルバーという二つ目の側面について説明します。オフラインソルバーは通常バッチ処理で動作し、問題を取り込んで実行し、完了するまで待つ必要があります。ソルバーが完了した時点で、最良の解または特定された最良の解を提供します。対して、オンラインソルバーはベストエフォートのアプローチで動作します。まずまず通用する解を見つけ、その後、時間の経過とともにまた投入する計算資源に応じて、より良い解に向けた反復を行います。オンラインソルバーで問題に取り組む最大の利点は、プロセスをいつでも一時停止して初期の候補解を得られるという点にあります。さらに、そのプロセスを再開することさえ可能です。古典的な数学的ソルバーは通常、プロセスの終了まで待つ必要があるバッチソルバーなのです。
残念ながら、サプライチェーンの現場での運用は、これまでの講義でも触れたように非常に波乱に満ちたものになることがあります。通常なら数学的最適化プロセスを例えば3時間かけて実行できる状況でも、ITの不具合、現実の問題、またはサプライチェーン上の緊急事態が発生する場合があります。そのような場合、通常3時間かかる作業が5分で中断され、たとえ質が悪くとも何らかの答えを提供してくれることは、まさに命の恩人と言えるでしょう。軍隊には「最悪の計画は計画がないことである」という格言があるように、全くの無策よりも粗雑な計画でもある方が良いのです。これこそが、オンラインソルバーが提供する価値なのです。これらが、今後の議論で念頭に置くべき主要な設計要素です。
さて、数学的最適化へのアプローチに関するこの講義の第一部を締めくくるために、ディープラーニングの講義内容を見てみましょう。ディープラーニングは機械学習の分野において完全な革命をもたらしました。しかし、本質的には、ディープラーニングもまた数学的最適化問題を内包しているのです。私は、ディープラーニングが数学的最適化そのものに革命をもたらし、最適化問題に対する我々の見方を根本的に変えたと信じています。ディープラーニングは、数学的最適化の最新のあり方を再定義したのです。
今日、最大規模のディープラーニングモデルは1兆(すなわち1,000億)以上のパラメータを扱っています。これを比喩的に言えば、ほとんどの数学的ソルバーは1,000変数すら扱うのに苦労し、いくら多くの計算ハードウェアを投入しても、通常は数万変数程度で限界に達してしまいます。それに対し、ディープラーニングは大量の計算資源を用いて成果を上げており、実現可能です。実際、1兆を超えるパラメータを持つディープラーニングモデルが実運用され、そのすべてのパラメータが最適化されているということは、数学的最適化プロセスが1兆パラメータにまでスケール可能であることを意味しており、これは古典的な最適化のアプローチで見たパフォーマンスとは全く異なるものです。
さらに興味深いのは、碁やチェスのような完全に決定論的で、非統計的、離散的かつ組み合わせ的な問題ですら、最も効率的に解かれているのは、完全に確率的かつ統計的な手法であるという点です。これは、一見すると離散的な最適化問題とみなされる碁やチェスが、今日では完全に確率的・統計的な手法で最も効率的に解決されているという事実に、科学界が20年前に抱いていた直感とは正反対の結果となっています。
それでは、ディープラーニングによって明らかにされた数学的最適化に関する理解を振り返ってみましょう。まず最初に、次元の呪いという概念を徹底的に再検討する必要があります。私はこの概念が大部分において誤っていると考えており、ディープラーニングは、最適化問題の難しさを考える上でこの概念が必ずしも正しくないことを示しています。数学的な問題のクラスを見ていくと、ある問題は完全に解くのが極めて困難であると数学的に証明できる場合があるのです。例えば、NP困難な問題について耳にしたことがあるでしょう。問題に次元を追加するごとに解くのが指数関数的に難しくなり、各次元が問題をより困難にし、累積的な障壁が生じると証明できます。限られた計算資源で問題を完璧に解くことはどのアルゴリズムにも期待できないのです。しかし、ディープラーニングは、この見方自体が大部分で誤っていたことを示したのです。
まず、問題の表現的複雑性と本質的複雑性を区別する必要があります。これら二つの概念を例を挙げて明確にしましょう。最初に示した時系列予測の例を見てみます。例えば、3年間の日次集計された売上履歴があるとします。つまり、約1,000日の日次の時間ベクトルがあり、これが問題の表現となるのです。
さて、もしこの表現を1秒単位の時系列表現に切り替えるとどうなるでしょうか? これは同じ売上履歴ですが、日次集計の代わりに1秒単位で集計して表現するということです。1日には86,400秒あるため、問題の表現のサイズと次元は86,000倍にまで膨れ上がることになります。
しかし、本質的な次元について考えると、売上履歴が存在することや、日次集計から1秒集計に変えること自体が、問題の複雑性、もしくは次元的複雑性を1,000倍に増加させるわけではありません。おそらく、1秒単位に集計すると、時系列データは非常に希薄になり、ほとんどの区間がゼロになるでしょう。つまり、問題が持つ本質的な次元性が10万倍に増加するわけではないのです。ディープラーニングは、多次元の表現があるからと言って、問題自体が本質的に困難になるわけではないことを明らかにしているのです。
次元性に関連するもう一つの視点として、ある問題がNP完全であると証明できたとしても(例えば、旅行セールスマン問題―この講義の冒頭で示された車両経路問題の簡略版)、旅行セールスマン問題自体は厳密にはNP困難問題として知られています。つまり、一般的な場合に最適解を見つけようとすると、地図上に地点を追加するたびに指数関数的な計算コストがかかる問題なのです。しかし実際には、two-optヒューリスティックが示すように、これらの問題は非常に少ない計算資源で優れた解を得ることができるため、数学的証明が一部の問題が非常に難しいと示しても、それが必ずしも近似解が悪いということを意味しません。近似解で十分であれば、その近似が非常に優れている場合もあり、時には近似と呼ばれるものではなく最適解が得られる場合もあるのです。ただし、その最適性を証明できないだけです。これは、問題を近似できるかどうかについて何も示しておらず、次元の呪いに悩まされるとされる問題の多くが、実は注目すべき次元がそれほど高くないため、解決は意外と簡単であることを示しています。ディープラーニングは、多くの非常に困難だと考えられていた問題が、実際にはそれほど難しくなかったことを成功裏に実証しました。
第二の重要な洞察は局所最小値です。数学的最適化やオペレーショナルリサーチに取り組む大多数の研究者は、局所最小値が存在しない凸関数を用いてきました。長い間、凸関数以外に取り組む人々は、いかにして局所最小値に陥らないかを模索してきました。その多くの努力はメタヒューリスティクスのような手法に向けられてきました。しかし、ディープラーニングは新たな理解をもたらしました―すなわち、局所最小値を気にする必要はない、ということです。この理解は、ディープラーニングコミュニティから生まれた最近の研究に起因しています。
もし次元が非常に高ければ、問題の次元が増加するにつれて局所最小値は消失することが示せます。低次元の問題では局所最小値は非常に頻繁に現れますが、問題の次元を数百あるいは数千に増やすと、統計的には局所最小値が現れる可能性は信じられないほど低くなります。ましてや、次元が何百万に達すれば、局所最小値は完全に消えてしまいます。
高次元を敵と考えるのではなく、問題の次元をあえて膨張させ、局所最小値が全く存在しないほどに明快な降下を実現できたらどうでしょうか? 実際、これこそがディープラーニングコミュニティや1兆パラメータを持つモデルで行われているアプローチです。この方法は、勾配降下法によって前進する非常に明快な方法を提供します。
本質的に、ディープラーニングコミュニティは、下降の質や最終的な収束性の証明が重要ではなく、重要なのは降下速度であることを示しました。つまり、非常に優れた解に向かって迅速に反復と降下を繰り返すことが求められます。もしより速い降下プロセスがあれば、最終的に最適化の面でより遠くへ進むことができるのです。これらの洞察は、20年前までの数学的最適化における一般的な理解に反するものです。
ディープラーニングから学ぶべき他の教訓も豊富に存在します。その一つがハードウェアシンパシーです。円錐計画法や幾何学的プログラミングのような数学的ソルバーは、計算ハードウェアではなく数学的直感を優先するため、もしハードウェアに反するソルバーを設計してしまうと、どんなに数学が優れていても、計算ハードウェアの効率的な利用ができず、結果として非常に非効率になる可能性が高いのです。
ディープラーニングコミュニティの主要な洞察の一つは、計算ハードウェアと上手く協調し、それを積極的に活用するソルバーを設計すべきだということです。これが、私が「現代コンピュータによるサプライチェーンのための補助科学」という一連の講義を始めた理由でもあります。持っているハードウェアとその最善の利用方法を理解することは非常に重要です。このハードウェアシンパシーこそが、たとえそれに大規模なコンピュータクラスターやスーパーコンピュータが必要だとしても、1兆パラメータを持つモデルを実現する方法なのです。
ディープラーニングからのもう一つの教訓は、代理関数(サロゲート関数)の利用です。従来、数学的ソルバーは問題自体をそのまま最適化しようとしていましたが、ディープラーニングは場合によっては代理関数を用いたほうが良いことを示しました。例えば、予測においては、ディープラーニングモデルは平均二乗誤差の代わりにクロスエントロピーを誤差指標として用いることが非常に多いのです。実際のところ、実世界でクロスエントロピーを誤差指標として重視する人はほとんどおらず、その挙動はむしろ奇妙です。
では、なぜ人々はクロスエントロピーを使用するのでしょうか? それは非常に急峻な勾配を提供するからです。ディープラーニングが示したように、重要なのは降下速度です。急峻な勾配があれば、非常に速く下降できます。「もし平均二乗誤差を最適化したいのであれば、なぜクロスエントロピーを使うのか? 対象がそもそも異なるではないか」と異議を唱える人もいるでしょう。しかし実際には、クロスエントロピーを最適化すれば非常に急峻な勾配が得られ、最終的に平均二乗誤差で評価しても、ほとんどの場合、より良い解が得られるのです。ここでは説明を単純化しています。代理関数の考え方は、真の問題は絶対的なものではなく、最終的な解の有効性を評価するための制御手段に過ぎないというものです。これは、ソルバーが進行中に使用するものでは必ずしもありません。これは、ここ数十年に渡って人気を博してきた数学的ソルバーの考え方とは全く逆です。
最後に、パラダイムに基づいて作業することの重要性があります。数学的最適化では、エンジニアリングの労働分業が暗黙のうちに存在します。数学的ソルバーに付随する暗黙の分業とは、ソルバーの設計を担当する数学エンジニアと、問題を数学的ソルバーが処理しやすい形に表現する問題エンジニアに分かれて作業するというものです。この分業は広く行われ、問題エンジニアには問題をできる限り簡潔かつ純粋な形で表現させ、ソルバーに処理を任せるという考え方がありました。
しかし、ディープラーニングはこの見方が極めて非効率的であることを示しました。この恣意的な分業は、最適化問題に取り組む上で最善の方法ではありません。結果として、数学エンジニアが担当する最適化問題が、あまりにも困難な状況に陥ってしまうのです。はるかに良い方法は、問題エンジニアが一層努力して問題を再構築し、数学的最適化器がより効果的に最適化できるようにすることです。
ディープラーニングは、ソルバーの上に問題をフレーム化するための一連のレシピに関するものであり、これにより最適化器の力を最大限に引き出せるのです。ディープラーニングコミュニティでの多くの発展は、TensorFlow、PyTorch、MXNetなど既存のソルバーのパラダイム内で効果を発揮する、学習に優れたレシピの構築に集中しています。結論として、問題エンジニア、あるいはサプライチェーンの用語で言えばサプライチェーン・サイエンティストと協働することが本当に重要なのです。

さて、今回の講義の中で最も価値ある文献の要素に関する、第二部かつ最後のセクションに進みましょう。ここでは、ローカルサーチと微分可能プログラミングという、二大ソルバー群を取り上げます。

まず、「プログラミング」という用語について改めて考えてみましょう。この言葉は非常に重要です。なぜなら、サプライチェーンの観点から、私たちは直面している問題、または直面していると考える問題を明確に表現したいからです。問題を、例えば円錐などの半ば馬鹿げた数学的仮説に無理やり合わせた、低解像度なものにしてしまいたくはありません。本当に求めているのは、本物のプログラミング・パラダイムにアクセスできることなのです。
覚えておいてください。線形計画法、二次円錐計画法、幾何学的プログラミングなどの数学的ソルバーはすべて、「プログラミング」というキーワードを伴って登場しました。しかし、過去数十年で、私たちがプログラミング・パラダイムに求めるものは劇的に進化しました。現代では、ループ、分岐、場合によってはメモリアロケーションなどを含む、ほぼ任意のプログラムを扱えるものが求められるのです。限られたおもちゃのようなバージョンではなく、できるだけ実際のプログラムに近いものが望まれます。サプライチェーンにおいては、全く正確に間違っているよりも、おおむね正しい方が良いのです。

一般的な最適化に対処するため、まずローカルサーチから始めましょう。ローカルサーチは、一見単純な数学的最適化手法です。その擬似コードでは、ランダムな解(ビットの集まりとして表現される)から始め、解をランダムに初期化し、その周辺を探索するためにビットをランダムに反転させます。そして、もしこのランダム探索によってより良い解が見つかれば、それが新たな基準解となります。
この驚くほど強力なアプローチは、文字通りどんなプログラムに対してもブラックボックスとして機能し、既知のどんな解からも再出発することが可能です。この手法をさらに改善する方法は数多く存在します。一つは微分計算であり、これは微分可能計算と混同してはならない概念です。微分計算とは、ある解でプログラムを実行した後に一ビットだけ反転させ、プログラム全体を再実行することなく、差分実行を行うという考え方です。もちろん、その効果は問題の構造に大きく依存します。プロセスを高速化する一つの方法は、操作中のブラックボックスプログラムに関する追加情報を利用するのではなく、プログラム自体を高速化することであり、依然として主にブラックボックスとして扱うというものです。
ローカルサーチを改善するための他のアプローチも存在します。実行するムーブの質を向上させることが可能です。最も基本的な戦略は、kフリップスと呼ばれ、k個のビットを反転させる方法で、kはごく少数(数個から十数程度)です。単にビットを反転させるだけでなく、問題エンジニアに対して、解に適用するべき変異の種類を指示させることもできます。例えば、問題に何らかの順列操作を適用したいと表明することができるのです。こうした賢明なムーブは、問題における特定の制約の充足をしばしば維持し、ローカルサーチの収束を促進します。
ローカルサーチをさらに向上させる別の方法は、探索空間を完全にランダムに探るのではなく、正しい方向を学習し、最も有望な反転箇所を特定することです。最近のいくつかの論文では、ローカルサーチの上に小さなディープラーニングモジュールを組み込み、ジェネレーターとして機能させる試みが示されています。しかし、このアプローチは、機械学習プロセスによって導入されるオーバーヘッドが計算資源面でプラスの効果を生むことを保証する必要があるため、エンジニアリング上の難点が存在します。
その他にもよく知られたヒューリスティクスは存在し、現代のローカルサーチエンジンの実装に必要な要素を非常に包括的に知りたい場合は、「LocalSolver: A Black-Box Local-Search Solver for 0-1 Programs」という論文を読むとよいでしょう。LocalSolverを運営する企業は、同名の製品も提供しています。この論文では、プロダクショングレードのソルバー内部で何が起こっているのか、エンジニアリングの視点から解説されています。彼らは、より良い結果を得るためにマルチスタートとシミュレーテッドアニーリングを利用しています。
ローカルサーチに関して付け加えるべき注意点の一つは、確率的な問題に対しては、自然な形ではうまく対処できないということです。確率的な問題では、「より良い解が見つかった」と単に宣言して即座にその解を最良解と決定するのは容易ではなく、さらに複雑な工夫が必要なのです。

さて、次に本日議論する第二のソルバー群、すなわち微分可能プログラミングに移りましょう。しかしその前に、微分可能プログラミングを理解するためには、確率的勾配降下法を理解する必要があります。確率的勾配降下法は、反復的かつ勾配に基づく最適化手法であり、1950年代初頭に開拓された一連の技法として登場しました。したがって、その歴史はほぼ70年に及びます。それは約6十年にわたりニッチな存在であり、ディープラーニングの進展によってその真の潜在能力と威力が遂に認識されたのです。
確率的勾配降下法は、損失関数が複数の構成要素に加法的に分解できると仮定しています。式中、Q(W)は損失関数を表し、それが一連の部分関数Qiに分解されます。これは、多くの学習問題が、複数の事例に基づいて予測を学習するという見方ができるため、非常に重要な仮定です。つまり、損失関数は、データセット全体における平均誤差と、各データポイントにおける局所誤差として分解できるのです。同様に、多くのサプライチェーンの問題も、このように加法的に分解することが可能です。例えば、サプライチェーンネットワークを各SKUごとのパフォーマンスに分解し、それぞれに損失関数を付与することができます。そして、最終的に最適化したい真の損失関数は、その総和となるのです。
この分解が整えば、学習問題にとって非常に自然な方法で、確率的勾配降下法 (SGD) のプロセスを反復できます。パラメータベクトル W は非常に大規模な系列になる可能性があり、最新のディープラーニングモデルでは1兆個のパラメータを有しています。考え方は、プロセスの各ステップで、少量の勾配を適用してパラメータを更新することです。イータ(η)は学習率であり、通常は0と1の間の小さな数値、しばしば約0.01です。Q のナブラは、部分損失関数 Qi の勾配を表します。驚くべきことに、このプロセスは非常にうまく機能します。
確率的勾配降下法は、次の i 要素をランダムに選ぶため「確率的」と呼ばれます。データセット内を飛び回りながら、各ステップでパラメータにごく僅かな勾配を適用するのがその本質です。
この手法は約60年間、比較的ニッチであり、広くコミュニティからも無視され続けました。なぜなら、確率的勾配降下法が全く機能するとは驚くべきことであったからです。これは、損失関数のノイズと、損失関数自体にアクセスする計算コストとの間で優れたトレードオフを提供するからです。全データセットに対して損失関数を評価する代わり、確率的勾配降下法では1つのデータポイントごとに少量の勾配を適用できます。この評価は断片的かつノイジーですが、そのノイズが非常に高速であるため問題ありません。全データセットを処理する場合に比べ、はるかに多くの微小でノイジーな最適化を実行できるのです。
驚くべきことに、導入されたノイズは勾配降下法を助けます。高次元空間での問題の一つは、局所的な最小値がほとんど存在しなくなることですが、依然として勾配が非常に小さく、下降方向が定まらない広大なプラトーに直面する場合があります。ノイズは、より急峻でノイジーな勾配をもたらし、下降を助けます。
勾配降下法の興味深い点は、それ自体が確率的プロセスでありながら、確率的な問題にも追加の変更なしで対応できることです。もし Qi がノイズを含む確率的関数で、評価するたびに結果がランダムに変わる場合でも、アルゴリズムの一行も変える必要はありません。確率的勾配降下法は、サプライチェーンの目的に完全に適合するパラダイムを提供するため、極めて重要です。

第2の疑問は、勾配はどこから来るのかということです。プログラムがあり、単に部分損失関数の勾配を求めるだけですが、この勾配はどこから得られるのでしょうか?任意のプログラムに対して、どのようにして勾配を計算できるのでしょうか?実は、以前から発見されていた非常にエレガントでミニマルな技法―自動微分―があるのです。
自動微分は1960年代に登場し、時と共に洗練されました。前向きモード(1964年に発見)と逆向きモード(1980年に発見)の2種類が存在します。自動微分は、一種のコンパイル技法と見なすことができ、損失関数を表すプログラムを持っていると、そのプログラムを再コンパイルして第2のプログラムを生成し、第2のプログラムの出力が損失関数ではなく、損失関数の計算に関与する全パラメータの勾配になるのです。
さらに、自動微分は初期プログラムと基本的に同一の計算複雑性を持つ第2のプログラムを提供します。つまり、勾配を計算するための第2のプログラムを作成できるだけでなく、その計算性能も初期プログラムとほぼ同じです。計算コストでは定数倍の増加に過ぎません。しかし実際には、第2のプログラムは初期プログラムと全く同じメモリ特性を持つわけではありません。細かな点は本講義の範囲を超えていますが、質問の際に議論できるでしょう。基本的に、逆向きと呼ばれる第2のプログラムはより多くのメモリを必要とし、場合によっては初期プログラムよりもはるかに多くのメモリを消費することがあります。より多くのメモリは計算性能に問題を引き起こすため、一様なメモリアクセスが保証されるわけではありません。
自動微分がどのようなものかを少し説明すると、前述のように前向きモードと逆向きモードの2種類があります。学習やサプライチェーン最適化の観点からは、逆向きモードのみが関心の対象です。画面に表示されているのは、完全に作り話の損失関数 F です。2つの入力値 X1 と X2 に対して関数を計算するために行われる一連の算術的または基本的な演算の前向きトレースが見え、これにより最終値を計算するための全ての基本ステップが示されます。
基本的な各ステップ―多くは乗算や加算などの単純な算術演算―に対して、逆向きモードは同じステップを逆順に実行するプログラムです。前向きの演算値の代わりに、逆向きでは随伴が得られます。各算術演算に対して、その逆の対応物が存在し、前向き演算から逆の対応物への遷移は非常に単純です。
複雑に見えるかもしれませんが、前向き実行と逆向き実行があり、逆向き実行は各操作に対して適用される基本的な変換に過ぎません。逆向き処理の最後に勾配が得られます。自動微分は複雑に見えるかもしれませんが、実際はそうではありません。私たちが最初に実装したプロトタイプは100行にも満たないコードで、非常にシンプルで実質的には低コストなトランスパイル技法でした。
ここで興味深いのは、我々が非常に強力な最適化手法である確率的勾配降下法を有しているという点です。これは驚くほどスケーラブルで、オンラインで利用でき、手書きでも問題なく、確率的な問題をネイティブに扱えます。残された唯一の課題は勾配の取得方法であり、自動微分を用いることで、ほぼ定数のオーバーヘッドで任意のプログラムに対する勾配を得ることが可能になります。最終的に得られるのは、微分可能なプログラミングです。
興味深いことに、微分可能なプログラミングは確率的勾配降下法と自動微分の組み合わせです。これら2つの技法は数十年前から存在していましたが、FacebookのAI責任者 Yann LeCun が2018年初頭からこの概念について発信し始めたことで、注目を浴びるようになりました。LeCun がこの概念を発明したわけではありませんが、その普及に大きく貢献したのです。
例えば、ディープラーニングコミュニティは当初、自動微分ではなくバックプロパゲーションを使用していました。ニューラルネットワークに詳しい方ならご存知の通り、バックプロパゲーションは自動微分よりもはるかに複雑なプロセスであり、実装も桁違いに困難です。あらゆる面で自動微分が優れているといえます。この洞察により、ディープラーニングコミュニティはディープラーニングにおける学習の構成要素を洗練させ、数学的最適化と各種学習技法を組み合わせる中で、微分可能なプログラミングが非学習部分を明確に分離する概念として生まれました。
トランスフォーマーモデルなどの最新のディープラーニング技法は、その下地として微分可能なプログラミング環境が動作していることを前提としています。これにより、研究者はその上に構築される学習側面に専念できるのです。微分可能なプログラミングはディープラーニングの基盤であると同時に、統計的予測のようなサプライチェーン学習プロセスの支援にも非常に関連性があります。
ディープラーニングと同様、この問題は2つの部分に分けられます。すなわち、基盤層としての微分可能なプログラミングと、その上に構築される最適化または学習技法です。ディープラーニングコミュニティは、トランスフォーマーのような微分可能なプログラミングに適したアーキテクチャを特定することを目指しています。同様に、最適化目的に適したアーキテクチャを見極める必要があり、これは囲碁やチェスのような高度に組合せ的な環境での学習手法にも応用されてきました。後の講義では、サプライチェーン特有の最適化に有効な技法について議論します。

さて、ここで締めくくりに移りましょう。サプライチェーンに関する文献や、そのほとんどのソフトウェア実装は、数学的最適化に関して非常に混乱しているのが現状です。この側面は通常、適切に識別されておらず、その結果、実務家、研究者、さらにはエンタープライズソフトウェア企業で働くソフトウェアエンジニアですら、数学的最適化の要素を雑然とした数値レシピに混ぜ合わせてしまいます。これは大きな問題であり、数学的最適化の性質を持つ一要素が十分に認識されていないため、人々が文献にあるものを理解できず、しばしば粗雑なグリッドサーチや性急なヒューリスティックに頼った結果、予測不可能で一貫性のないパフォーマンスに終始してしまうのです。講義の締めくくりとして、今後サプライチェーンの数値手法または解析機能を謳うソフトウェアに出会った際は、数学的最適化の観点から何が行われているのか、何が実施されているのかを必ず問い直す必要があります。もし、提供者がこの視点について明瞭な説明をしていなければ、それはあなたが図の左側にいる可能性が高く、その場所は決して望ましいものではありません。
さて、次に質問を見てみましょう。

質問: オペレーションにおいて、計算手法への移行は必須のスキルであり、運用担当の役割は陳腐化するのか、それとも逆なのでしょうか?
まず、いくつか明確にしておきたいことがあります。こうした懸念をCIOに押し付けるのは誤りだと考えています。CIOは既に、計算資源、低レベルのトランザクションシステム、ネットワークの信頼性、サイバーセキュリティといった、ソフトウェア基盤の層を管理する責任があり、供給連鎖に実際の価値をもたらすために何が必要かを理解することは求められていません。
問題は、多くの企業でコンピュータに関する知識が極端に不足しているため、CIOがあらゆる事柄の頼りの存在になってしまうことです。実際、CIOは基盤層を担当すべきであり、各専門家が利用可能な計算資源やソフトウェアツールを使って各自のニーズに対処すべきなのです。
運用担当の役割が陳腐化するという点については、もしあなたの役割が一日中Excelのスプレッドシートを手作業でチェックすることであれば、その役割は確実に陳腐化するでしょう。これは1979年にラッセル・アコフが論文を発表して以来知られている問題です。問題の本質は、この意思決定手法が未来のものではないと認識されていたにもかかわらず、長い間現状が維持され続けた点にあります。企業は実験的プロセスを理解する必要があるのです。
あなたは資本主義的な付加価値を提供する必要があり、これはサプライチェーン向けソフトウェア製品のプロダクト指向デリバリーについての私の以前の講義に戻るものです。要点は、あなたが会社にどのような資本主義的付加価値を提供するかということです。もし何も提供できなければ、あなたは会社が将来目指すべき姿に属していない可能性が高いのです。
質問: Excelソルバーを使ってMRMSC値を最小化し、alpha、beta、gammaの最適な値を求めるというのはどうでしょうか?
この質問はホルト・ウィンタース法の場合に関連があると思います。グリッドサーチで実際に解が見つかるのです。しかし、このExcelソルバーでは一体何が行われているのでしょうか?それは勾配降下法なのでしょうか、それとも別の手法なのでしょうか?もしExcelの線形ソルバーのことを指しているのであれば、問題は線形ではないため、Excelは何もできません。もしExcel内の他のソルバーやアドインを指しているなら、動作はするかもしれませんが、これは非常に古い視点です。確率的な考え方を取り入れておらず、得られる予測は非確率的なもので、時代遅れのアプローチとなります。
Excelが使えないというわけではありませんが、問題はExcelでどのようなプログラミング機能が解放されるかにあります。専用アドインを追加すれば、Excelで確率的勾配降下法を実行することは可能かもしれません。Excelは任意のプログラムを上乗せしてプラグインできるため、理論上はExcelで微分可能なプログラミングを行うことも可能です。しかし、Excelでそれを実践するのは良い考えではありません。なぜなら、サプライチェーン向け製品指向のソフトウェアデリバリ―の概念に立ち返り、Excelで何が問題となっているのか―すなわちプログラミングモデルと、チームでの長期的な作業維持が可能かどうか―を理解する必要があるからです。
質問: 最適化問題は通常、車両ルーティングや予測に偏っています。では、サプライチェーン全体の最適化はどうでしょうか?個々の領域を別々に見るよりも、コスト削減につながるのではないでしょうか?
完全に同意します。サプライチェーン最適化の呪いとは、部分問題に対して局所最適化を行うと、全体のサプライチェーンの問題を解決するのではなく、問題を先送りにしてしまう可能性が非常に高くなるという点にあります。完全に同意します。そして、より複雑な問題に取り組むときは、たとえばreplenishment戦略と組み合わせた車両ルーティング問題のようなハイブリッドな問題に直面することになります。問題は、制約されずに済むよう非常に汎用的なソルバーが必要であるということです。もし非常に汎用的なソルバーがあれば、車両ルーティングにのみ有効なtwo-optのようなスマートなヒューリスティックスに依存するのではなく、より汎用的なメカニズムを持たなければなりません。
この全体論的な視点に移行するためには、次元の呪いを恐れてはいけません。20年前、人々はこれらの問題はすでに極めて困難であり、巡回セールスマン問題のようなNP完全問題だと言っていたため、さらに別の問題と絡め合わせた、より難しい問題を解決しようとするのは無謀だと考えられていました。しかし答えはイエスです。そうする能力が必要であり、多くの絡み合い交錯した問題の統合が、最終的な解決策となるからです。
確かに、これらの問題を個別に解決しようとする考え方は、全体を一括して解決する方法に比べればるかに弱いものです。間違いなく正確であるよりも、概ね正しい方が良いのです。局所的にマイクロ最適化して他の場所で問題を生む高度な局所最適化手法を用いるより、サプライチェーン全体を一つのシステム、ひいては一つのブロックとして扱う非常に弱いソルバーを用いた方がはるかに良い結果が得られます。システム全体の真の最適化は、必ずしも各部分で最適化されるものではないため、会社全体やサプライチェーン全体の利益のために最適化すれば、他の側面も考慮することから局所的には最適にならないのは当然のことです。
質問: 最適化の演習を実施した後、いつscenarioを再検討すべきでしょうか? 新たな制約が突然現れる可能性があるという前提からの質問です。 答えは、最適化は頻繁に再検討すべきだということです。これは、このシリーズの第2講義で私が提示したサプライチェーン科学者の役割そのものです。サプライチェーン科学者は、必要に応じて最適化を何度も見直します。たとえば、スエズ運河を巨大な船が塞ぐといった予期せぬ新しい制約が現れた場合でも、サプライチェーンにおけるこのdisruptionに対処しなければなりません。さもなければ、導入したシステムは誤った条件下で動作し、意味不明な結果を生み出すでしょう。たとえ緊急事態でなくても、会社に最大のリターンをもたらす可能性が高い角度を検討するために時間を投資すべきです。これは根本的に研究開発のプロセスであり、システムは構築され稼働しているものの、改善の余地を見出すための応用研究プロセスなのです。サプライチェーン科学者として、終日数値手法を試しても既存の結果以上の効果が得られない日もあれば、小さな微調整で非常に幸運に数百万の節約につながる日もあります。不規則なプロセスですが、平均すると成果は非常に大きく得られます。
質問: 線形計画法、整数計画法、混合計画法、さらにはウエーバーや商品のコストに関する場合以外で、最適化問題のユースケースは何でしょうか?
私は逆にこう問いたいです。サプライチェーンの問題において、線形計画法がどこに適用可能だと思われますか? サプライチェーンの問題が線形であるケースは事実上存在しません。私の反論は、これらのフレームワークが非常に単純すぎて、玩具問題すらも扱えないという点にあります。前述したように、線形計画法のような数学的フレームワークでは、古く低次元なパラメトリック予測モデルの厳しい冬の最適化のような玩具問題にさえ対処できません。巡回セールスマン問題やその他ほとんどの問題にさえも対応することができないのです。
整数計画法や混合整数計画法は、いくつかの変数を整数とするという一般的な表現に過ぎません。とはいえ、これらのプログラミングフレームワークがサプライチェーン問題に必要な表現力には程遠い、玩具のような数学的枠組みであるという事実は変わりません。
最適化問題のユースケースについて尋ねるなら、サプライチェーンのpersonasに関する私の全講義をご覧になることをお勧めします。私たちはすでにサプライチェーン・ペルソナのシリーズを展開しており、数学的最適化を通じてアプローチできる問題を山ほどリストアップしています。これらの講義では、パリ、マイアミ、アムステルダム、さらにはワールドシリーズなどが取り上げられており、今後も更に増えていく予定です。適切な数学的最適化の視点で取り組むべき問題は多数存在しますが、そのすべての問題を、これらの数学的フレームワークが生み出す極めて厳格で奇妙な制約内に収めることはできません。改めて言えば、これらの数学的フレームワークは主に凸性に依存しており、サプライチェーンにとっては最適な視点とは言えません。私たちが扱うほとんどの問題は非凸であるため、非凸であるからといって解が得られないわけではありません。結局のところ数学的証明がなくても、上司や会社は意思決定の根拠として証明を求めるのではなく、利益を上げる判断ができるかどうかを重視するのです。生産、補充、価格設定、品揃えなどにおいて正しい決定が下せるかどうかが重要なのです。
質問: 学習アルゴリズムのデータは、学習支援のためにどのくらいの期間保存されるべきでしょうか?
そうですね、今日のデータストレージが非常に安価であることを考えると、なぜ永遠に保存しないのでしょうか?データストレージは信じられないほど安いのです。たとえば、スーパーマーケットに行けば、1テラバイトのハードドライブが60ドル前後で売られているのが分かるでしょう。つまり、非常に低コストなのです。
もちろん、データに個人情報が含まれている場合、そのデータを保持することが負債となるという別の懸念もあります。しかし、サプライチェーンの観点からは、そもそも個人情報を保持する必要はありません。クレジットカード番号や顧客の名前を保存する必要はなく、必要なのは顧客識別子などのみです。すべての個人情報を削除すれば、どのくらいの期間保持するかという問いには、永遠に保存すればよいということになります。
サプライチェーンにおける一つの要点は、データが限られているということです。画像認識などのディープラーニングの問題のように、ウェブ上のすべての画像を処理してほぼ無限のデータベースにアクセスできるわけではありません。サプライチェーンでは常にデータは限られており、たとえば将来の需要を予測する場合、過去10年以上のデータが次の四半期の需要予測に統計的に有意である産業は非常に少ないのです。それでも、データを捨ててしまってから後で不足していると気付くより、必要に応じてデータを切り詰めるほうが常に簡単です。ですから、私の提案は、すべてのデータを保持し、個人情報を削除した上で、data pipelineの最終段階で非常に古いデータをフィルタリングする方が良いかどうかを判断することです。場合によってはその方が良いかもしれませんし、そうでないかもしれません。それは業界によって異なります。たとえば、航空宇宙産業のように、部品や航空機の運用寿命が40年に及ぶ場合、過去40年分のデータをシステム内に保持していることは意義があるのです。
質問: 多目的プログラミングとは、2つ以上の目的、例えば複数の関数の和をとる、または複数の関数を1つの目標で最小化するという意味でしょうか?
多目的問題に取り組む方法には複数のバリエーションがあります。単に関数の和を取ればよいというわけではなく、和を取ると損失関数の分解や構造の問題に帰着してしまいます。本質的には、ベクトルとして複数の目的を扱うのです。実際、基本的には多目的プログラミングにはいろいろな手法が存在します。最も興味深いのは、辞書式順序付け(lexicographic ordering)を採用する手法です。サプライチェーンに関して言えば、多数の関数の平均や最大値を取って最小化する方法も関心を引くかもしれませんが、私ははっきりとは言えません。むしろ、制約を注入し、その制約を通常の最適化の一部として扱う多目的アプローチが、サプライチェーンにとって非常に有用だと考えています。他の手法も面白いかもしれませんが、私自身は確信が持てないのです。
質問: 最適解に対して近似解をいつ使用すべきか、どのように判断しますか?
つまり、質問の意図を完全に理解しているか自信はありませんが、ディープラーニングから学べる教訓の一つは、最適解というものは存在しない、ということです。すべてはある程度の近似に過ぎません。たとえ数字があると言っても、コンピューター上の数字は無限の精度を持たず、有限の精度でしか表現できません。そして、その有限の精度が、場合によっては逆効果となることもあります。つまり、答えは常に近似解であるということです。最大の教訓は、完璧な解が存在すると考えるのは幻想であるという点です。完璧で最適な解というものは存在せず、すべての解は近似であり、その精度に差があるだけです。ですから、数学的最適化の観点からは、品質を評価するための損失関数があり、最終的に競合する2つの解があれば、その損失関数でどちらが優れているかを判断する、ということになります。それがこの仕組みなのです。
質問: なぜ、歴史的データとしての時系列は、そもそも86,400で割られたのでしょうか?
割られたわけではありません。あくまで一例です。時系列に取り組む際、古典的な時系列予測アルゴリズムでは、等間隔の時系列、すなわち同じ長さのビンに集計する方法を採用するという、状況をあえて馬鹿げた状態に持っていくための例示にすぎません。時系列を表現する方法は数多く存在しますが、最も一般的なのは日次や週次のように均一なバケツで集計する等間隔型の時系列です。この方法なら、バケツの長さがすべて同じとなり、系列はきれいなベクトル状の構造を持つのです。
しかし、私が指摘したいのは、時系列の集計が大いに恣意的であるということです。データを日次データとして表すこともできれば、秒単位で表すこともできます。秒単位でデータを表現することに意味があるのでしょうか? 答えはイエスです。問題の種類によります。たとえば、電力会社でグリッドを管理する場合、電力の供給と消費の正確なバランスを取るために毎秒の電力量を管理する必要があります。そして、そのバランスは秒単位で調整されるのです。地域の店舗での販売では意味をなさないかもしれません。ちなみに、86,400という数字は、24時間×60分×60秒に過ぎません。ここで強調したかったのは、常にデータの表現方法が存在し、その表現方法(特定の次元性を持つ)とデータ本来の内在的な次元性(全く異なる可能性がある)を混同してはならないという点です。表現は大部分が作り話であり、恣意的なものです。たとえば、3年分のデータを持つという数値的なindicatorにより、1000次元のベクトルが得られるとされます。しかし、この1000という次元は、日次集計という決定に基づいており、ほとんどが恣意的なものです。もし他の集計期間を選べば、全く異なる次元になるでしょう。これが私の言いたかったポイントであり、ディープラーニングが本当に正しかった点でもあります。すなわち、データの恣意的な表現選択に惑わされず、表現にとらわれないことが重要なのです。
質問: 確率的予測を導入することで、コスト関数や制約条件も確率的な性質を帯びることになりますが、これは解を見つけるプロセスにどのような影響を及ぼすのでしょうか?
ええ、基本的かつ根本的な制約が一つあります。もし、確率的問題を処理できないソルバーを用いていると、確率的問題から決定論的問題へは大量のサンプルの平均を取ることで必ず戻ることができるとはいえ、計算コストの面で大きな問題に直面することになります。つまり、満足のいく解に到達するために、代替案と比べて約1万倍の処理能力を必要とするということです。これは、使用している数学的最適化ツールやインフラが、確率的問題にネイティブに対応できるようになっている必要があることを意味します。まさに、微分可能プログラミングがそれを実現しており、局所探索では難しいですが、局所探索も改善・改良することで、そのような状況下でもスムーズに動作させることが可能となります。
根本的に、確率的予測を採用する場合、未来の見方に挑戦するだけでなく、その予測を扱うためのツールや計測機器そのものにも大きな挑戦を突き付けます。これこそが、Lokadが過去10年間にわたって開発してきたツールのあり方なのです。サプライチェーンの問題にはほぼすべて不確実性という要素が含まれており、結果としてすべての問題がある程度確率的な問題に該当するため、そのような問題にうまく対応できるツールが必要とされるのです。
素晴らしい。それでは次の講義は同じ曜日の水曜日に行われます。その間に休暇があります。次の講義は9月22日に予定されており、皆さんにお会いできるのを楽しみにしています。今回はサプライチェーンのための機械学習について議論します。それではまた。
参考文献
- オペレーションズ・リサーチの未来は過去にある, Russell L. Ackoff, 1979年2月
- LocalSolver 1.x: 0-1プログラミングのためのブラックボックスローカルサーチソルバー, Thierry Benoist, Bertrand Estellon, Frédéric Gardi, Romain Megel, Karim Nouioua, 2011年9月
- 機械学習における自動微分: サーベイ, Atilim Gunes Baydin, Barak A. Pearlmutter, Alexey Andreyevich Radul, Jeffrey Mark Siskind, 最終改訂 2018年2月


