00:01 はじめに
01:56 M5不確実性チャレンジ - データ (1/3)
04:52 M5不確実性チャレンジ - ルール (2/3)
08:30 M5不確実性チャレンジ - 結果 (3/3)
11:59 これまでの経緯
14:56 これから(おそらく)起こること
15:43 ピンボールロス - 基礎 1/3
20:45 負の二項分布 - 基礎 2/3
24:04 イノベーション・スペース・ステート・モデル (ISSM) - 基礎 3/3
31:36 売上構造 - REMTモデル 1/3
37:02 統合 - REMTモデル 2/3
39:10 集約レベル - REMTモデル 3/3
43:11 単一段階学習 - 議論 1/4
45:37 パターン完成 - 議論 2/4
49:05 欠落パターン - 議論 3/4
53:20 M5の限界 - 議論 4/4
56:46 結論
59:27 次回講義と聴衆からの質問
説明
2020年、Lokadのチームは世界的予測コンペティションM5において909チーム中5位を達成しました。しかし、SKUレベルで集計すると、その予測は1位となりました。需要予測はサプライチェーンにとって極めて重要です。このコンペティションで採用された手法は、他の上位50社が採用した典型的な手法とは異なり非定型的なものでした。この成果から学べる教訓は多く、サプライチェーンにおけるさらなる予測課題への前奏となります。
全文書き起こし

このサプライチェーン講義シリーズへようこそ。私はジョアンネス・ヴェルモレルです。本日は「M5予測コンペティションにおけるSKUレベルでのNo1」を発表いたします。正確な需要予測は、サプライチェーン最適化の柱の一つとされています。実際、すべてのサプライチェーン決定は未来に対する予測を伴っています。より優れた未来予測を得ることで、サプライチェーンの目的にかなった定量的に優れた意思決定が可能となります。したがって、最先端の予測精度を実現するモデルの特定は、サプライチェーン最適化にとって極めて重要かつ関心の高いテーマです。
本日はシンプルな売上予測モデルをご紹介します。このモデルはその単純さにもかかわらず、Walmartから提供されたデータセットに基づく世界的予測コンペティションM5においてSKUレベルで第1位を獲得しました。本講義には2つの目的があります。第一の目的は、最先端の売上予測精度を実現するために必要な要素を理解することです。この理解は、後の予測モデリングへの取り組みにおいて基盤となります。第二の目的は、サプライチェーン向けの予測モデリングに関する適切な視点を確立することです。この視点は、今後のサプライチェーンにおける予測モデリングの発展を導くためにも用いられます。

M5は2020年に開催された予測コンペティションです。この競技会は、予測分野の著名な研究者Spyros Makridakisにちなんで名付けられました。今回で第5回目の開催となりました。これらのコンペティションは数年ごとに開催され、使用されるデータセットの種類に応じて焦点が異なります。M5はサプライチェーン関連の課題であり、使用されたデータセットはWalmartが提供した小売店データでした。今後開催予定のM6チャレンジは、金融予測に焦点を当てる予定です。
M5で使用されたデータセットは、もともと公開データセットであり、現在もそのままです。これはWalmartの小売店データを日次単位で集計したもので、約30,000のSKUが含まれていました。小売の観点から見ると、これはかなり小規模なデータセットです。一般的に、1つのスーパーマーケットは約20,000のSKUを持ち、Walmartは10,000以上の店舗を運営しています。したがって、このM5データセットは、サプライチェーンの観点からは世界規模のWalmartデータセットのおよそ0.1%未満に相当しました。
さらに、以下でご覧いただくように、M5データセットには欠落しているデータクラスが存在しました。そのため、私の概算では、このデータセットは実際にはWalmart規模で必要とされる全体の約0.01%に近いものと考えられます。それにもかかわらず、このデータセットは実環境で予測モデルの堅実なベンチマークを作成するには十分な規模です。実運用ではスケーラビリティに細心の注意を払う必要がありますが、予測コンペティションの観点からは、ほとんどの手法―たとえ非効率な手法であっても―が利用可能となるよう、データセットを十分小さくするのは妥当です。また、これにより参加者が利用できる計算資源の量によって制約を受けることがなくなります。
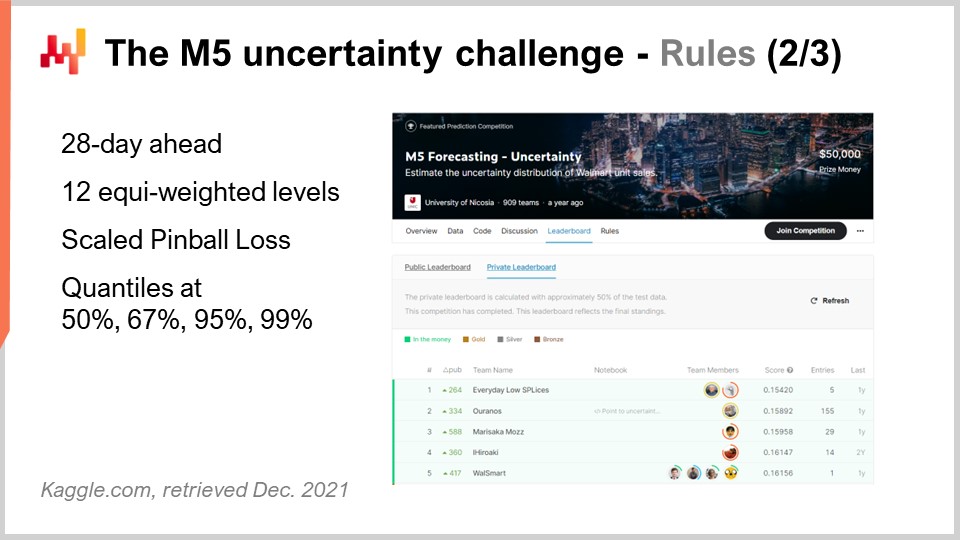
M5コンペティションでは、AccuracyとUncertaintyという2つの異なるチャレンジが行われました。ルールはシンプルで、すべての参加者がアクセスできる公開データセットがあり、これらのチャレンジの一つまたは両方に参加するために、各参加者は自身の予測データセットを作成し、Kaggleプラットフォームに提出する必要がありました。Accuracyチャレンジは平均時系列予測、すなわち最も標準的な形式の予測を提供することが求められ、具体的には約40,000の時系列に対して日次の平均予測を行うものでした。一方、Uncertaintyチャレンジは分位点予測の提供が求められました。分位点予測は意図的なバイアスを伴います。これこそが分位点を用いる本質的な意味です。本講義ではUncertaintyチャレンジにのみ焦点を当てます。なぜなら、サプライチェーンにおいては、予期せぬ高需要がストックアウトを引き起こし、予期せぬ低需要が在庫の償却を招くためです。サプライチェーンのコストは極端な状況に集中しており、私たちが注目すべきは平均値ではありません。
実際、Walmartにおける平均の意味を考えると、ほとんどの製品、ほとんどの店舗、ほとんどの日において観測される平均販売数はゼロです。したがって、ほとんどの製品は微小な平均予測値となります。このような平均予測はサプライチェーンの観点からはあまり意味がありません。選択肢が在庫ゼロにするか1単位を補充するかの場合、平均予測はほとんど意味を持たないのです。これは小売業に限ったことではなく、FMCG、航空宇宙、製造業、ラグジュアリーなど、ほぼすべての業界で同様の状況です。
改めてM5 Uncertaintyチャレンジに戻ると、50%、67%、95%、99%の4つの分位点を算出する必要がありました。これらの分位点目標は、すなわちサービスレベルのターゲットと考えることができます。これらの分位点予測の精度は、ピンボールの損失関数という指標で評価されました。本講義では後ほどこの誤差指標について再度触れます。

このUncertaintyチャレンジには世界中から909チームが参加しました。Lokadのチームは全体では5位ながら、SKUレベルでは第1位を獲得しました。実際、SKUは時系列全体の約75%を占めていましたが、州からSKUまで様々な集約レベルが存在し、これら全てが最終スコアにおいて同等の重み付けをされていました。したがって、SKUが時系列の約75%を占めていたとしても、最終スコアに占める割合は約8%にすぎませんでした。
Lokadのこのチームが採用した手法は、「A White Box ISSM Approach to Estimate Uncertainty Distribution of Walmart’s Sales」という論文で発表されました。本講義終了後、この動画の説明欄にこの論文へのリンクを掲載する予定です。論文では、すべての要素がより詳細に説明されています。明確かつ簡潔にするため、本講義ではこの論文で提示されたモデルを、共著者4名のイニシャルに由来するBRAMPTモデルと呼びます。
画面上には、M5の上位5件の結果が表示されています。これは、予測コンペティションの結果に関する一般的な洞察を与える論文から取得されたものです。ランキングの詳細は選択された指標に大きく依存しており、それ自体はそれほど驚くべきことではありません。Uncertaintyチャレンジでは、スケールされた形のピンボール損失関数が使用されました。この誤差指標については後ほど再度触れます。M5 Uncertaintyチャレンジは、現在の私たちの予測手法では不確実性を排除できないことを示しましたが、これは決して驚くべき結果ではありません。小売店の売上が不規則かつ断続的であることを考えると、不確実性を完全に無視するのではなく、受け入れることの重要性が改めて強調されます。しかし、サプライチェーンのソフトウェアベンダーがこの予測コンペティションの上位50に一人も入っていなかったのは、彼らが自社の最先端予測技術を誇っているとされることを考えると、なおさら注目に値します。
さて、本講義は一連のサプライチェーン講義の一部です。本講義は、このシリーズの第5章目の最初の講義となります。この第5章は予測モデリングに特化しています。確かにサプライチェーンを最適化するためには定量的な洞察の獲得が必要です。材料の購入、製品の生産、在庫の移動、または販売商品の価格の引き上げや引き下げなど、サプライチェーンに関する意思決定は、将来の需要に対する予測を伴います。いずれのサプライチェーン決定にも、将来に対する暗黙の期待が内包されているのです。この期待は潜在的で隠れたものですが、将来に対する期待の質を向上させるためには、その期待を具体化する必要があり、通常は予測によって行われます。ただし、それが必ずしも時系列予測である必要はありません。
今回の第5章は、「予測」ではなく「予測モデリング」と名付けられています。その理由は2点あります。第一に、予測はほとんどの場合、時系列予測と結びつけられるからです。しかし、この章で示すように、多くのサプライチェーンの状況は時系列予測の視点に必ずしも適合しません。この観点から、予測モデリングはより中立的な用語と言えます。第二に、真の洞察をもたらすのはモデリングそのものであり、単なるモデル自体ではないからです。私たちはモデリングの技術を求めており、これらの技術を通じて実世界のサプライチェーンで直面する多様な状況に対処できると期待しています。
本講義は、予測モデリングの章の序章として、予測モデリングが単なる予測への空想的思考ではなく、最先端の予測技術として成立することを示すものです。さらに、この章を進める中で次第に明らかになるその他多数の利点も併せ持っています。
本講義の残りは3部構成となります。第一部では、BRAMPTモデルの構成要素となる数学的要素を復習します。第二部では、これらの要素を組み合わせ、M5コンペティション時と同様にBRAMPTモデルを構築します。第三部では、BRAMPTモデルの改善点、およびM5コンペティションで提示された予測チャレンジそのものの改善点について議論します。

M5のUncertaintyチャレンジは、将来の売上の分位点推定を求めるものです。分位点とは一次元分布上のある点を指し、定義上、90%分位点とはその値より下になる確率が90%、上になる確率が10%である点です。中央値は、定義上50%の分位点となります。
ピンボール損失関数は分位点と深い親和性を有する関数です。基本的に、0から1の間の任意のtau値は、サプライチェーンの観点からサービスレベルのターゲットと解釈できます。任意のtau値に対し、そのtauに対応する分位点は、ピンボール損失関数を最小化する確率分布内の値となります。画面上には、サプライチェーン最適化のためにLokadが開発したドメイン固有言語Envisionで記述された、ピンボール損失関数のシンプルな実装が示されています。その構文はPythonに近く、聴衆にも比較的理解しやすいものです。
このコードを詳しく見てみると、実際の値を示すy、我々の推定値であるy-hat、そして分位点目標であるtauが存在します。改めて言うと、分位点目標は基本的にサプライチェーンにおけるサービスレベルのターゲットです。ここでは、過小評価の場合はtauの重みが、過大評価の場合は1- tauの重みが付けられていることがわかります。ピンボール損失関数は、絶対誤差の一般化です。tauが0.5の場合、ピンボール損失関数は単なる絶対誤差となり、絶対誤差を最小化する推定値を得ると、それは中央値の推定値となります。
画面上にはピンボール損失関数のプロットが表示されています。この損失関数は非対称であり、非対称損失関数を用いることで、平均や中央値の予測ではなく、制御されたバイアスを持つ予測、まさに分位数推定に必要な予測を得ることができます。ピンボール損失関数の素晴らしさはそのシンプルさにあります。もしこのピンボール損失関数を最小化する推定値を持っていれば、構造的に分位数予測が得られるのです。したがって、パラメータを持つモデルで、そのパラメータの最適化をピンボール損失関数の視点で行えば、モデルからは本質的に分位数予測モデルが得られるのです。
M5 Uncertainty チャレンジでは、50、67、95、99 の4つの分位数ターゲットが提示されました。私はこのような分位数ターゲットの連続を通常「分位数グリッド」と呼びます。分位数グリッド、または量子化グリッド予測は、完全な確率予測というには及びません;近いですが、まだその域には達していません。分位数グリッドでは、依然としてターゲットを選別している状態にあります。たとえば、95パーセントの分位数予測を生成したいとした場合、「なぜ95なのか?なぜ94や96ではないのか?」という疑問が生じます。この疑問には答えがありません。この章の後半でさらに詳しく見ていきますが、この講義内では割愛します。確率予測の最大の利点は、分位数グリッドにおけるこの選別的側面を完全に排除できる点にあると言っておきましょう。
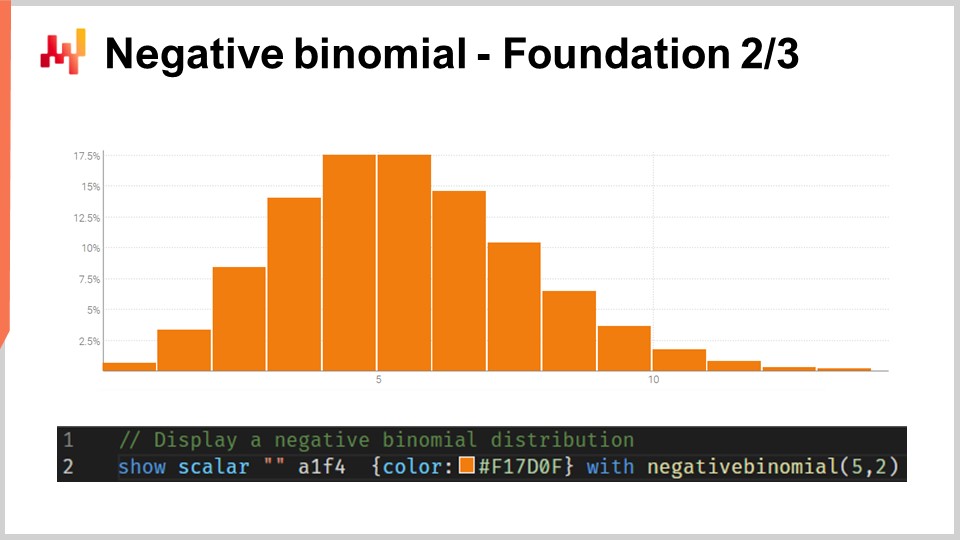
おそらく聴衆のほとんどは、自然現象に非常に頻繁に現れる正規分布、すなわちガウスの鐘形曲線に馴染みがあるでしょう。カウント分布とは、各整数に対して確率が割り当てられる分布です。正規分布のような連続実数分布とは異なり、カウント分布は非負の整数のみを扱います。カウント分布には多くの種類がありますが、ここで注目するのは REM モデルで使用される負の二項分布です。
負の二項分布は、正規分布と同様に2つのパラメータを持ち、これらが分布の平均と分散を効果的に制御します。もし負の二項分布の平均と分散を、確率分布の大部分の質量がゼロから十分離れた位置にくるように選べば、全ての確率値を最も近い整数に寄せ集めた場合、漸近的に正規分布の挙動に収束します。しかし、特に平均が小さく、分散に比べて低い場合、負の二項分布は正規分布と比べて挙動が大きく乖離することがわかります。特に、平均が小さい負の二項分布では、分布が非常に非対称となり、どんな平均と分散を選んでも常に対称である正規分布とは大きく異なります。 画面上には、Envision を用いてプロットされた負の二項分布が表示されています。このプロットを生成したコードは以下に示されています。この関数は2つの引数をとります。なぜならこの分布には2つのパラメータがあるからであり、結果として得られるのはヒストグラムとして表示されるランダム変数に他なりません。ここでは負の二項分布の細かい仕様に深入りはしません。これは基本的な確率論であり、最頻値、中央値、累積分布関数、歪度、尖度などに対する明示的な閉形式解析式が存在します。Wikipedia のページはこれらの式についてかなり良い概要を提供しているので、もしこの特定のカウント分布について詳しく知りたい場合は参照することをお勧めします。
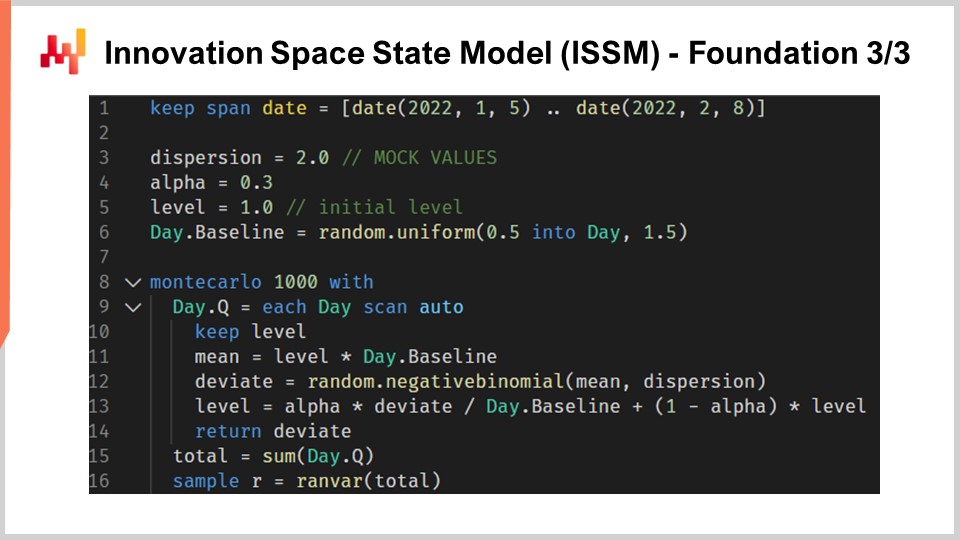
次に、Innovation Space State Model、または ISSM へ進みます。Innovation Space State Model とは、非常に長く壮大な名前ですが、実際にはかなりシンプルな処理を行うモデルです。実際、ISSM は時系列をランダムウォークへと変換するモデルです。ISSM を使えば、単なるバニラな時系列予測、つまり各期間ごとに平均値が1つ設定される予測を、分位数予測だけでなく直接確率予測に変換することができます。画面上には、再び Envision で書かれた完全な ISSM の実装が表示されています。コードは十数行のみで、そのほとんどが大きな処理を行っていないことがわかります。ISSM は非常に単純で、他の言語、たとえば Python でもこのコードを再実装するのは非常に容易です。
それでは、これらのコード行の詳細を見ていきましょう。1行目では、ランダムウォークが発生する期間の範囲を指定しています。M5 の観点では、28日間のランダムウォークが必要なため、1日あたり1ポイント、合計28ポイントがあります。3行目、4行目、5行目では、ランダムウォーク自体を制御するパラメータ群を導入しています。最初のパラメータは分散(dispersion)で、これは ISSM プロセス内で発生する負の二項分布の形状を制御する引数として用いられます。次に alpha があり、これは ISSM 内部で行われる指数平滑プロセスを制御する因子そのものです。5行目では、レベルがあり、これはランダムウォークの初期状態を示します。そして最後に、6行目では、通常、予測モデルに組み込みたいあらゆるカレンダーパターンを捉えるための一連の因子が導入されます。
さて、3行目から6行目の値は全てモックの初期化値として設定されています。簡潔さのため、これらの値が実際にどのように最適化されるかは後ほど説明しますが、ここで示されている初期化は全てモック値に過ぎません。ベースラインのために単にランダムな値を割り当てているだけです。実際にこのモデルを使用する場合、これらの値を適切に初期化する必要がある点については、後ほどこの講義で触れます。
では、ISSM プロセスの核心部分を見ていきましょう。核心は8行目から始まり、1000回の反復ループで構成されています。先ほど述べたように、ISSM プロセスはランダムウォークを生成するプロセスであり、ここでは1000回、つまり1000のランダムウォークを生成します。これより多くても少なくても構いません;これはシンプルなモンテカルロ・プロセスです。続いて9行目では、第2のループを実行しています。これは、対象期間の各日を1日ごとに反復するループです。外側のループはランダムウォークごとに1回の反復を行い、内側のループはそのランダムウォーク内で1日から次の日へと進む1回の反復を行っています。
10行目では、レベルの保持を行っています。レベルを保持する、つまりこのパラメータは内側のループ内で変動し、外側のループ間では変動しないという意味です。すなわち、レベルは各日ごとに変化しますが、モンテカルロ・ループを通じて1つのランダムウォークから次のランダムウォークへ移る際には、上で宣言された初期値にリセットされます。11行目では、平均値を計算します。平均値は、負の二項分布を制御するために使用される第2のパラメータです。12行目では、通常の二項分布に従って乱数の偏差値(deviate)を抽出します。乱数の偏差値を抽出するとは、このカウント分布からランダムサンプルを取得することを意味します。続いて13行目では、得られた偏差値に基づいてレベルを更新します。この更新プロセスは、alpha パラメータによって導かれる非常にシンプルな指数平滑プロセスです。もし alpha を非常に大きく、すなわち1と設定した場合は、最新の観測値に全重量を置くことを意味します。一方、alpha を0に設定すると、変動がなく、ベースラインで定義された元の時系列に忠実となります。
ちなみに、Envision で「.baseline」と記されている部分は、テーブルが存在することを示しており、例えば NDM5 というテーブルがあり、そのテーブルには28個の値が存在し、baseline はそのテーブルに属するベクトルに過ぎません。15行目では、全ての偏差値を「someday.q」を通して集計し、合計を「total」という変数に格納しています。すなわち、各ランダムウォークにおいて、全ての日の偏差値の合計が計算され、28日間の総販売数が得られるのです。最後に16行目では、これらのサンプルを「render」に集約しています。render とは Envision における特定のオブジェクトであり、本質的には正および負の整数の相対的な確率分布そのものです。
まとめると、ISSM は1次元ランダムウォークを生成するランダム生成器として機能します。販売予測の観点からは、これらのランダムウォークを、実際の販売の将来の観測値として捉えることができます。ここで興味深いのは、予測を平均や中央値としてではなく、将来の1つの可能性の実現例として考えている点です。

ここまでで、REMT モデルを組み立てるために必要な全ての要素を揃えました。
REMT モデルは、Holt-Winters 予測モデルを彷彿とさせる乗法的構造を採用しています。各日には、5つのカレンダー効果の積として算出されるベースライン値が割り当てられます。具体的には、年の月、曜日、月の日、クリスマス、ハロウィンの効果です。この考え方は、簡潔な Envision スクリプトとして実装されています。
Envision には、テーブル間でブロードキャスト可能なリレーショナル代数が備わっており、これはこのケースに非常に有用です。5つのカレンダーパターンごとのテーブル(各テーブルはグループ化されたテーブルとして構築される)と日付テーブルが構築されます。日付テーブルには「date」という主キーがあり、新しいテーブルを「by」集約と共に日付を指定して宣言することで、日付テーブルとの直接のブロードキャスト関係を構築しています。
曜日テーブルを具体的に見ると、4行目で、まさに7行分のテーブルを構築しています。テーブルの各行は、曜日テーブル内の1行と一対一で対応付けられます。したがって、この曜日テーブルに値を設定すれば、受け側である日付テーブルの各行が、自然にその曜日テーブル内の1行と対応付けられるのです。
9行目では、ベクトル「de.dot.baseline」が、右辺の5つの因子の単純な乗算として計算されています。これらすべての因子は最初に日付テーブルへブロードキャストされ、その後、日付テーブルの各行ごとに単純な行単位乗算が行われます。
これで、数十のパラメータを持つモデルが完成しました。パラメータを数えると、1月から12月までの各月に対して12個、曜日に対して7個、月の日に対して31個のパラメータがあります。しかし、NDM5 では、各 SKU ごとに全ての値に対して個別のパラメータを学習するわけにはいかず、パラメータ数が莫大になり Walmart のデータセットに対して過剰適合してしまうためです。その代わり、NDM5 ではパラメータ共有という手法が活用されました。
パラメータ共有とは、各 SKU ごとに別々のパラメータを学習するのではなく、サブグループを確立し、そのグループ単位でパラメータを学習する手法です。そして、そのグループ内で同じパラメータ値を使用します。パラメータ共有は、deep learningにおいて広く用いられている非常に古典的な手法であり、ディープラーニング以前から存在していました。M5 の期間中、月と曜日のパラメータは店舗部門単位で学習されました。後ほど、M5 の様々な集約レベルについて説明します。月の日に関しては、実際には州レベル、すなわちカリフォルニアやテキサスなど、アメリカの各州においてハードコーディングされた因子が用いられていました。M5 の期間中、これらのカレンダーのパラメータは、関連するスコープ内での直接平均として単純に学習されました。つまり、同一スコープに属する全 SKU の値を平均化し、正規化するという非常に直接的な方法でパラメータが設定されたのです。

ここまでで、REMT モデルを組み立てるための全てが揃いました。これまでに、全てのカレンダーパターンを組み込んだ日次ベースラインの構築方法を示しました。カレンダーパターンは、あるcrudeだが効果的な学習メカニズムを通して、直接平均で学習されました。また、ISSM が時系列をランダムウォークに変換する仕組みも示しました。あとは、ISSM のパラメータ、すなわち内部で行われる指数平滑プロセスに使用する alpha、負の二項分布の制御に用いる dispersion、そしてランダムウォークの初期化に用いる初期レベルの適切な値を確立するだけです。
M5 コンペティションの期間中、Lokad のチームは、残る3つのパラメータを学習するために単純なグリッドサーチ最適化を活用しました。グリッドサーチとは、これらの値の全ての組み合わせを、小刻みに増分させながら探索する手法です。グリッドサーチは、前述のピンボール損失関数を指標として、これらの3パラメータの最適化を導きました。各 SKU に対してグリッドサーチはおそらく最も非効率的な数学的最適化手法の一つですが、パラメータがたった3つで、各時系列ごとに1回の最適化が必要な点、さらに M5 データセット自体が比較的小さいことから、M5 コンペティションには適していました。
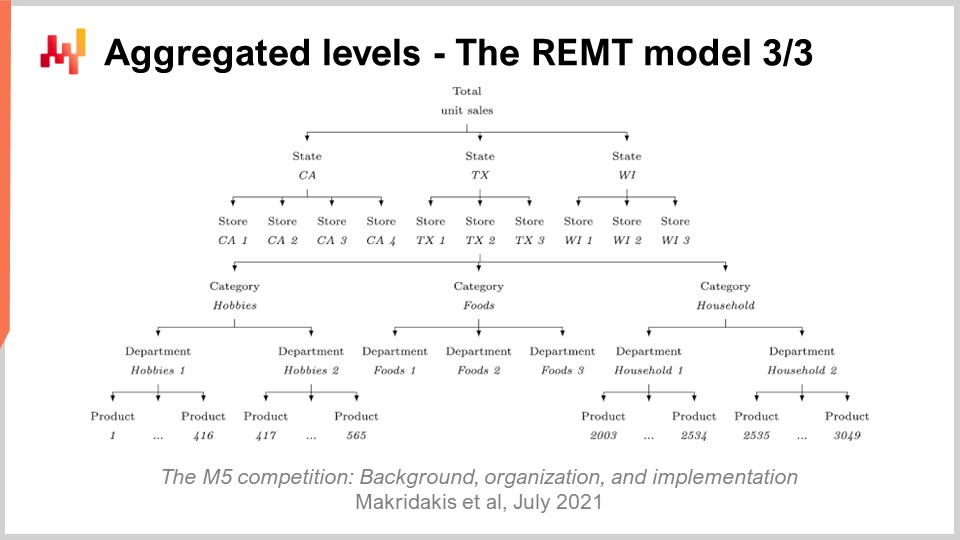
ここまで、REMTモデルがSKUレベルでどのように動作するかを紹介してきました。しかしながら、M5では12の異なる集約レベルが存在しました。最も細分化されたSKUレベルは最も重要でした。SKU、すなわち在庫管理単位とは、文字通り1つの製品が1箇所に存在することを意味します。同じ製品が10箇所にある場合、10のSKUが存在します。SKUはサプライチェーンにおいて最も関連性のある集約レベルと考えられる一方で、在庫-補充-定義や品ぞろえなど、ほとんどすべての在庫関連の意思決定はSKUレベルで行われます。M5は主に予測コンペティションであったため、他の集約レベルにも多くの重点が置かれていました。
画面上では、これらのレベルがM5データセットに存在した集約レベルをまとめています。カリフォルニア州やテキサス州などの州が含まれているのがわかります。より高い集約レベルに対応するために、Lokadのチームは2つの手法を用いました。1つは、低い集約レベルでランダムウォークを行い、それらを合計して高い集約レベルでのランダムウォークを実現する方法、もう1つは学習プロセスを完全に再起動し、直接高い集約レベルにジャンプする方法です。M5の不確実性チャレンジでは、REMTモデルはSKUレベルで最も優れた成果を上げましたが、他の集約レベルでは最高ではなく、全体としては十分なパフォーマンスを発揮しました。
REMTモデルがすべてのレベルで最良でなかった理由に関する私自身の仮説は次のとおりです(これはあくまで仮説であり、実際に検証したものではありません):負の二項分布は、2つのパラメータを通じて2つの自由度を提供します。SKUレベルのような非常に疎なデータの場合、2つの自由度はアンダーフィッティングとオーバーフィッティングの適切なバランスを実現します。しかし、より高い集約レベルに移行するにつれて、データはより濃密で豊かになり、量的-供給-チェーン-マニフェストにおけるトレードオフは、分布の形状をより正確に捉えるのに適した何かへと変わる可能性があります。このため、これを達成するには追加の自由度、つまりおそらく1つか2つの追加パラメータが必要になるでしょう。
私は、REMTモデルの中核で使用されるカウント分布のパラメータ化の度合いを高めることで、より高い集約レベルにおいて最先端に迫る、あるいはほぼそれに匹敵する成果を得られたのではないかと考えています。とはいえ、実際にその時間はなく、将来的に再検討する可能性もあります。これで、M5コンペティション中にLokadチームが行った作業は終了となります。

どのようにすれば異なる、あるいはより良い結果が得られたのかを議論してみましょう。REMTモデルは低次元のパラメトリックモデルであり、シンプルな乗法構造を持っているにもかかわらず、M5中にパラメータの値を取得するために用いられたプロセスは、やや偶然にも複雑になっていました。多数の段階を経たプロセスで、各カレンダーパターンがそれぞれ特別な取り扱いを受け、最終的にカスタムグリッドサーチでREMTモデルが完成しました。この全工程はサプライチェーン-サイエンティストにとって非常に時間を要するものであり、多量のアドホックなコードが含まれているため、本番環境での運用にはかなり信頼性が低いと私は考えます。
特に私の考えでは、すべてのパラメータの学習プロセスを単一段階に統一するか、少なくとも同じ手法を繰り返し用いる形に統一すべきだと考えています。現在、Lokadはまさにそれを実現するために微分可能プログラミングを利用しています。微分可能プログラミングは、カレンダーパターンに関してアドホックな集約を行う必要性をなくし、すべてのパターンを一度に抽出することで、カレンダーパターン抽出の順序問題も解消します。さらに、微分可能プログラミング自体が最適化プロセスであるため、従来のグリッドサーチをはるかに効率的な最適化ロジックに置き換えます。今後のこの章の講義では、サプライチェーンにおける予測モデリングの文脈で、微分可能プログラミングがどのように活用できるかをさらに詳しく見ていく予定です。
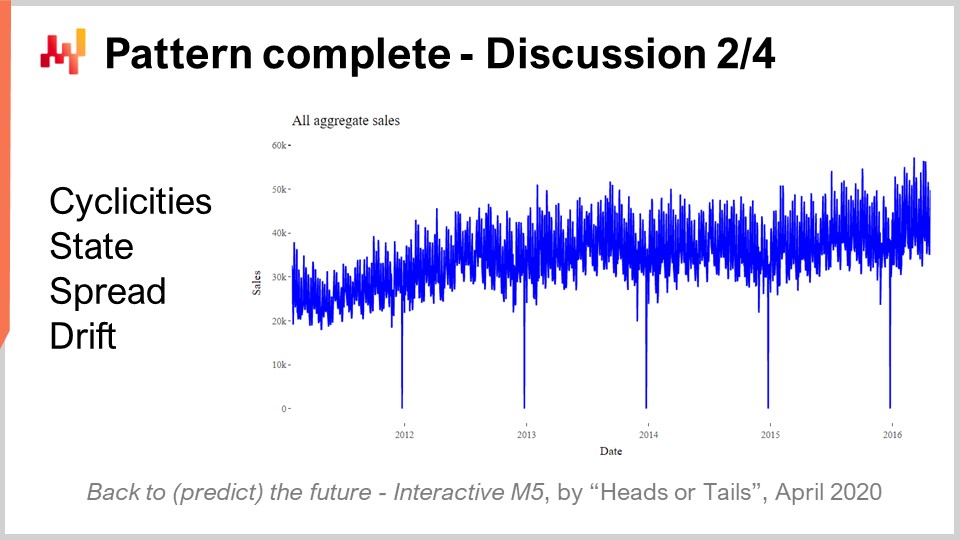
さて、M5コンペティションの最も驚くべき結果の一つは、どの統計的パターンにも名前が付けられなかったということです。実際、私たちはシンプルさ、状態、分散、そしてドリフトという4つのパターンだけを利用して、M5コンペティションにおける最先端の予測精度を達成しました。
シンプルさはすべてカレンダーに基づいており、いずれも全く驚くべきものではありません。状態は、特定の時点でSKUが達成した水準を表す単一の数値として表現できます。分散は、負の二項分布のパラメータ化に用いられる散布度を示す単一の数値で表され、ドリフトはSSM内で発生した指数平滑化プロセスに紐づく単一の数値で表現できます。28日間という期間に対しては、トレンドを加える必要すらありませんでした。
画面に表示されているM5の5年間の総売上を見ると、その集約は明らかに控えめな上向きの傾向を示しています。それにもかかわらず、REMTモデルはそれを考慮せずに動作し、精度に一切影響していませんでした。REMTモデルのパフォーマンスは、他に捉えるべきパターンが存在するのか、もしくは見落としているパターンがあるのかという疑問を提起します。
少なくとも、REMTモデルのパフォーマンスは、このコンペティションに参加したグラディエントブースティングツリーや深層学習手法など、より洗練されたモデルがあの4つのパターン以外の何ものも捉えられなかったことを示しています。実際、もしそれらのモデルが何かを大幅に捉えることができたならば、SKUレベルにおいてREMTモデルをはるかに凌駕していただろうに、それは起こりませんでした。ARIMAのようなその他の高度な統計手法についても同様のことが言えます。これらのモデルも、この非常にシンプルな乗法的パラメトリックモデルが捉えたもの以外の何ものも捉えることができませんでした。
オッカムの剃刀の原則が示すように、もしパターンが私たちの理解から逃れている、もしくはこのモデルのシンプルさを凌駕するほど非常に興味深い特性があるという明確な理由がなければ、REMTモデルと同等のシンプルなモデル以外を使用する理由はありません。

しかし、M5データセットの設計上の理由から、いくつかのパターンがM5コンペティションには存在しませんでした。これらのパターンは重要であり、実際の小売環境では、それらを無視するモデルはうまく機能しないでしょう。これは私自身の経験に基づいています。
まず、製品のローンチです。M5コンペティションでは、少なくとも5年間の販売履歴がある製品のみが対象となっていました。これはサプライチェーンの観点からは不合理な仮定です。実際、FMCG製品は通常、寿命が数年であるため、実際の店舗では1年未満の販売履歴しか持たない品ぞろえが常に大部分を占めています。さらに、リード-タイムが長い製品の場合、店舗で一度も販売される前に多数のサプライチェーン上の決定が行われなければなりません。したがって、ある製品に対して全くの販売履歴がなくても運用可能な予測モデルが必要です。
次に重要なパターンは品切れ(ストックアウト)です。品切れは小売業では発生しますが、M5コンペティションのデータセットではこれらが完全に無視されていました。しかし、品切れは売上を制限します。店舗で製品が在庫切れの場合、その日は販売されず、結果として観測される売上に大きなバイアスが生じます。ウォルマートや一般的な総合小売店の場合、現行在庫を記録する電子データは完全には信頼できず、数多くの在庫の不正確さが存在するため、これも考慮に入れる必要があります。
三番目に、プロモーションがあります。M5コンペティションでは過去の価格情報は含まれていましたが、予測対象期間の価格データは提供されなかったため、このコンペティションの参加者は価格情報を活用して予測精度を向上させることができなかったようです。REMTモデルは価格情報を全く使用していません。予測期間の価格情報が欠如していたという点に加え、プロモーションは単に価格の問題だけではありません。店舗で目立って展示されることで製品がプロモートされ、価格が下がっていなくても需要が大幅に増加する可能性があります。さらに、プロモーションにおいてはカニバリゼーションや代替効果も考慮する必要があります。
全体として、サプライチェーンの観点から見れば、M5データセットはおもちゃのようなものです。サプライチェーンのベンチマークを行うための現存する最高のパブリックデータセットであるにせよ、実際の小規模な小売チェーンの本番環境と真に同等のものとは程遠いのです。

しかし、M5コンペティションの制約は単にデータセットに起因するものではありません。サプライチェーンの観点からは、M5コンペティションを実施するためのルール自体に根本的な問題があります。
最初の根本的な問題は、売上と需要を混同しないことです。すでに品切れの問題でこの点に触れました。サプライチェーンの観点からは、本当に求められるのは売上ではなく、需要を予測することです。しかし、この問題はさらに深刻です。需要を適切に推定することは、本質的に教師なし学習の問題です。店舗の品ぞろえが恣意的に決定されているからといって、製品の需要を推定すべきでないということにはなりません。どの店舗の品ぞろえに含まれているかに関係なく、製品の需要を推定しなければなりません。
第二の側面は、分位点予測が確率的予測よりも有用性に欠けるということです。サービスレベルを選り好みするような手法は全体像に隙間を生じさせ、分位点予測はサプライチェーンの利用という点で比較的弱いです。確率的予測は完全な確率分布を提供するため、はるかに包括的なビジョンをもたらし、この種の問題を解消します。確率的予測の唯一の重大な欠点は、予測が生成された後に下流で何かを行う際、より多くのツールが必要になる点です。ちなみに、REMTモデルはモンテカルロ法を通じて全体の確率分布を生成できるため、実質的に確率的予測として機能します。単にモンテカルロの反復回数を調整する必要があるだけです。
小売業において、顧客は特定のSKUの視点や、そのSKUで達成されるサービスレベルに本質的な関心を持っているわけではありません。ウォルマートのような総合小売店における顧客の認識は、買い物かご全体によって形成されます。通常、顧客は単一の製品だけでなく、全体の買い物リストを念頭に店舗を訪れます。さらに、店舗には多数の代替品が存在します。単一のSKU指標だけでサービスの質を評価しようとすると、顧客が店舗で感じるサービスの質を完全に見逃してしまうのです。
結論として、時系列予測のベンチマークとしてM5コンペティションは、データセットと方法論の面で堅実ですが、サプライチェーンの観点から見ると時系列の視点そのものが不足しています。時系列データはサプライチェーンに存在するデータや、サプライチェーン上の問題を正確に反映しているわけではありません。M5コンペティション期間中、上位にははるかに洗練された手法が多く見られましたが、私の見解では、これらのモデルは実質的に行き詰まりであり、本番環境での運用にはすでに複雑過ぎる上、時系列の視点に固執しているため、我々のサプライチェーンのニーズに合わせて新たな視点に発展させる余地が全くありません。
むしろ、出発点としてはREMTモデルは申し分なく優れており、非常にシンプルな要素の組み合わせで構成されています。さらに、M5コンペティションのために組み合わせられた特定の構成を超えて、これらの要素を活用・組み合わせる方法は数多く存在することは容易に想像できます。M5コンペティションでREMTモデルが達成した順位は、これまでのところ、非常に複雑でデバッグが難しく、本番運用にも適さず、膨大な計算資源を消費するような複雑なモデルに移行する理由がないことを示しています。
本章後半の講義では、REMTモデルの要素やその他数多くの要素をどのように活用し、サプライチェーンで見られる多種多様な予測課題に対応できるかを見ていきます。重要な点は、モデルそのものは重要ではなく、モデリングのプロセスが重要であるということです。

質問: なぜ負の二項分布なのか?それを選んだ理由は何だったのか?
非常に良い質問です。実は、カウント分布の世界的な図鑑を見ると、おそらく20種類以上の広く知られているカウント分布が存在します。Lokadでは、内部のニーズに合わせて12種類ほどをテストしました。その結果、1つのパラメータのみを持つ非常に単純なカウント分布であるポアソン分布が、データが非常に疎な場合にはかなりうまく機能することが分かりました。ですからポアソン分布はかなり良いのですが、実際にはM5データセットはややリッチでした。ウォルマートのデータセットの場合、もう少し多くのパラメータを持つカウント分布を試しましたが、うまく機能するようでした。それが実際に最良であるという証拠はなく、おそらくより良い選択肢も存在するでしょう。負の二項分布にはいくつかの重要な利点があります。実装が非常に簡潔であり、また広範に研究されたカウント分布であるという点です。つまり、確率を計算するだけでなく、偏差のサンプリング、平均値の取得、累積分布の計算など、カウント分布に必要なあらゆるツールが備わっているのです。これはすべてのカウント分布に当てはまるわけではありません。
この選択には、ある程度の実用主義と論理が組み合わさっています。ポアソン分布は自由度が1つですが、負の二項分布は2つの自由度を持っています。さらに、ゼロインフレーション付き負の二項分布のような手法を用いれば、自由度が2.5程度になるなどの工夫も可能です。私は、このカウント分布に特定の決定的な価値があるとは断言しません。
質問: M5には他にもサプライチェーン最適化ソフトウェアのベンダーが存在しましたが、生産環境で十分にスケールするライブモデルを使用していたところはありませんでした。大多数は、重い機械学習モデルを使用しているのでしょうか?
まず、M5がデータサイエンスのプラットフォームであるKaggle上で行われたものであることを区別し、明確にしなければならないと言いたいです。Kaggleでは、可能な限り複雑な手法を使う大きなインセンティブがあります。データセットは小さく、時間に余裕があり、トップに立つためには他の参加者よりもわずか0.1%正確さを向上させるだけでよいのです。これが全てです。したがって、ほぼすべてのKaggleコンペティションでは、トップの順位が、その0.1%の精度向上のために非常に複雑な手法を用いた人々で埋め尽くされているのが見受けられます。つまり、予測コンペティションであるがゆえに、利用可能な最も重厚なモデルを含め、あらゆる手法を試す強いインセンティブが働くのです。
もし生産環境で実際にこれらの重い機械学習モデルが使用されているかと問われれば、私のざっくりとした観察では全く使用されていません。実際、それは非常に稀です。LokadというサプライチェーンソフトウェアベンダーのCEOとして、何百人ものサプライチェーンディレクターと話をしてきました。文字通り、大規模なサプライチェーンの90%以上はExcelで運営されています。大規模なサプライチェーンが勾配ブースト木やディープラーニングネットワークを使って運営されているのを見たことがありません。Amazonを除けば、実際にこのような技術を使用しているのは、Amazon、Alibaba、JD.comなど、ほんの数社、極めて大きなeコマース企業に限られます。しかし、彼らはこの点において例外的な存在です。一般的な大手FMCG企業や大規模な実店舗小売企業は、生産環境でこの種の技術を使用していません。
質問: 数学的および統計的な用語を多数挙げる一方で、小売販売の性質や主要な影響要因を無視しているのは奇妙です。
私は、これはコメントに近いものだと言いたいですが、むしろあなたに問いたいのは、あなたは一体何を提供できるのか、ということです。優れた予測技術を自慢するサプライチェーンベンダーが皆姿を見せないのは、まさにそれが理由です。もしあなたが絶対的に優れた予測技術を持っているのなら、なぜ公共のベンチマークのような場面であなたが現れないのでしょうか?もう一つの説明としては、人々がブラフをかけているということです。
小売販売の性質や多くの影響要因に関しては、私自身が使用されたパターンを列挙しました。そして、その4つのパターンを用いることで、REMTモデルはSKUレベルでの正確性において第一位となりました。もし、はるかに重要なパターンが存在すると主張するのであれば、その証明責任はあなたにあります。私自身の疑念としては、900以上のチームの中でそれらのパターンが観察されなかったということは、おそらくそのパターン自体が存在しないか、もしくは現在の技術ではそのパターンを捉えるのは極めて困難であり、実質的に存在しないのと同じである、ということです。
質問: M5の競合他社の中で、Lokadには及ばなかったものの、特に汎用的なアプリケーションに組み込む価値のあるアイデアを採用した者はいましたか?(名誉ある言及として)
私は競合他社に非常に注意を払ってきましたし、彼らもLokadに注目していると確信しています。しかし、そんな事例は見かけませんでした。REMTモデルは本当に唯一無二のものであり、事実上、他のトップ50の参加者がどのタスクにおいても採用した方法とは全く異なっていました。他の参加者は、機械学習コミュニティでより古典的とされる手法を用いていました。
コンペティション中には、非常に巧妙なデータサイエンスのテクニックがいくつか披露されました。たとえば、Walmartのデータセットに対して、データ拡張(augmentation)という非常に洗練された手法を駆使し、本来の規模よりもはるかに大きくすることで、わずか数パーセントの正確性向上を狙うというものがありました。これは、不確実性チャレンジで第一位にランクされた参加者によって実施されました。ここで正しい用語は「データ拡張」であり、「データの膨張」ではありません。データ拡張はディープラーニングの技法で一般的に使われますが、ここでは勾配ブースト木と共に、かなり珍しい方法で用いられていたのです。今回のコンペティションでは、華麗で非常に巧妙なデータサイエンスのトリックがいくつも示されました。これらのトリックがサプライチェーン全体にどれほど応用可能かは定かではありませんが、この章の後半で機会があれば、いくつか言及するかもしれません。
質問: SKUレベルを集約して上位のレベルを推計したのか、それとも中間から上位にかけて新たに計算したのか、どちらの場合も比較してどのような結果となったのですか?
パーセンタイルグリッドの問題点は、各目標レベルごとにモデルを個別に最適化しがちであることにあります。パーセンタイルグリッドでは、数値的不安定性により、99パーセンタイルが97パーセンタイルよりも低くなってしまう、いわゆるパーセンタイルの交差が発生する可能性があります。これは些細な問題で、通常は単に値の順序を入れ替えるだけで済みます。根本的には、これがパーセンタイルグリッドが完全な確率予測とは言えないと私が指摘した理由の一つです。解決すべき細かい問題は山積みですが、全体として見ると重要なものではありません。確率予測に移行すれば、これらの問題はそもそも存在しなくなるのです。
質問: もしソフトウェアベンダー向けの別のコンペティションをデザインするとしたら、どのようなものになるでしょうか?
正直なところ、私には分かりませんし、非常に難しい質問です。私の厳しい批判にもかかわらず、予測のベンチマークに関してはM5が現状最高のものだと考えています。しかし、サプライチェーンのベンチマークに関しては、実現可能かどうかすら完全には確信していません。いくつかの問題が実際には教師なし学習を必要とする、とほのめかしたとき、それは非常に厄介な問題でした。教師なし学習の領域に入ると、評価指標を持つという考えは放棄され、先進的な機械学習の全コミュニティでさえ、教師なしの状況下で優れた自動学習ツールを運用するということの意味を理解し切れていないのです。一体どのようにしてそのようなもののベンチマークを取るのでしょうか?
機械学習に関する私の講義に参加できなかった聴衆のために説明すると、教師ありの場合、基本的に入力と出力があり、出力の質を評価するための指標が存在するタスクを達成しようとします。しかし、教師なしの場合はラベルもなく、比較するものがないため、事態は大いに困難になります。さらに、サプライチェーンではバックテストすら不可能な事例が多々あります。教師なしの側面を超えて、バックテストという視点すらも完全に満足のいくものではありません。例えば、需要を予測すると、価格決定など特定の意思決定が生じます。もし価格を上げるか下げるかを決定すれば、それはあなたが下した決定であり、未来に永続的な影響を与えるのです。したがって、「今回は異なる需要予測をして、異なる価格決定を下し、そして歴史を繰り返す」と過去に戻って試すことはできません。バックテストのアイデアが機能しない側面は他にも多く存在します。だからこそ、私はコンペティションが予測の観点から非常に興味深いものであると信じています。それはサプライチェーンの出発点としては有用ですが、真にサプライチェーンに満足のいく解決策を求めるのであれば、さらに優れた、そして異なるアプローチが必要なのです。この予測モデリングに関する章では、なぜモデリングがこれほど注目に値するのかを示していきます。
質問: この手法は、データポイントが少ない状況で使用することは可能ですか?
絶対に可能だと思います。この章でREMTモデルを用いて示したような構造化モデリングは、データが非常にまばらな状況で特にその効果を発揮します。理由は単純で、多くの人間の知識をモデルの構造に組み込むことができるからです。モデルの構造は、どこからともなく引き出されたものではなく、Lokadチームが問題を深く理解した結果として生まれたものです。例えば、曜日や月などのカレンダーパターンについて、私たちはそれらを発見しようとはせず、Lokadチームは最初からそれらのパターンが既に存在していることを知っていました。唯一の不確実性は、月の日付パターンの出現率であり、多くの場合これが弱い傾向にあるという点です。Walmartのケースでは、米国にスタンププログラムが存在するという事実が、この月の日付パターンを非常に強固なものにしているのです。
データが少ない場合、この手法は非常に効果的に機能します。なぜなら、どんな学習メカニズムを用いようとも、あなたが課した構造を大いに活用するからです。もちろん、構造が間違っている場合はどうなるのかという疑問も生じますが、だからこそサプライチェーンに関する考察と理解が極めて重要であり、正しい意思決定が可能になるのです。最終的には、あなたは自らの任意の判断が良かったか悪かったかを評価する手段を持っていますが、基本的にはその評価はプロセスのかなり後の段階で行われます。この予測モデリングに関する章の後半では、航空、ハードラグジュアリー、エメラルドなど、非常にまばらなデータセットにおいて構造化モデリングがいかに効果的に使えるかを示します。こうした状況では、構造化モデルが真に輝きを放つのです。
次回の講義は2月2日(水曜日)の同じ時間、パリ時間午後3時に行われます。それでは、その時にお会いしましょう!


