Saisonalität (Supply Chain)

In supply chain zeigt die Nachfrage - oder der Verkauf - eines bestimmten Produkts Saisonalität, wenn die zugrunde liegende Zeitreihe im Jahresverlauf einer vorhersehbaren zyklischen Variation unterliegt. Saisonalität ist eines der am häufigsten verwendeten statistischen Muster, um die Genauigkeit von Nachfrageprognosen zu verbessern.

Veranschaulichung saisonaler Zeitreihen

Der folgende Graph veranschaulicht 4 saisonale Zeitreihen (zum Vergrößern anklicken). Die Zeitreihen werden wöchentlich über einen Zeitraum von 159 Wochen (etwa 3 Jahre) aggregiert. Die Daten stellen wöchentliche Sendungen von 4 unterschiedlichen Produkten aus dem Lager eines großen europäischen Einzelhändlers dar.

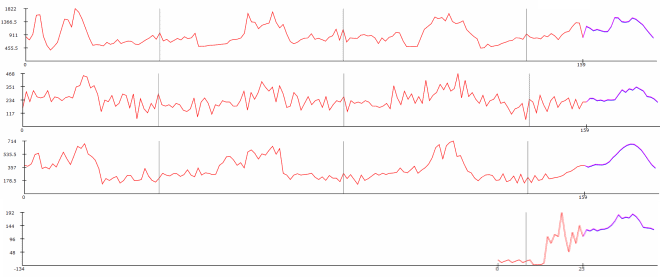
Der erste Tag des Jahres (1. Januar) ist mit einem grauen vertikalen Marker markiert. Die historischen Daten erscheinen in Rot, während die Lokad-Prognose in Lila dargestellt wird. Die Saisonalität kann visuell als Ähnlichkeit der Muster von einem Jahr zum nächsten beobachtet werden; verwenden Sie die grauen Marker als Referenzpunkte.

Basis-Modell für die saisonale Zerlegung

Sei Y(t) die Nachfrage zum Zeitpunkt t. Wir zerlegen die Nachfrage Y(t) in zwei Komponenten: S(t), eine strikt zyklische Funktion, und Z(t), das nicht-saisonale Ergänzungselement. Dies ergibt:

Y(t) = S(t) * Z(t) wobei S(t + 1 Jahr) = S(t)

Wenn eine solche Funktion S(t) geschätzt werden kann, verläuft der Prognoseprozess typischerweise in drei Schritten:

• Berechne die saisonbereinigte Zeitreihe als Z(t) = Y(t) / S(t).
• Erstelle die Prognose über die Zeitreihe Z(t), möglicherweise durch gleitenden Durchschnitt.
• Wende anschließend die Saisonalitätsindizes auf die Prognose an.

Zurück zum ursprünglichen Problem der Schätzung der saisonalen Indizes S(t): Unter der Annahme, dass es keinen Trend (unter anderem) gibt, kann S(t) mit folgender Methode geschätzt werden:

S(t) = MITTELWERT( Y(t-1)/MA(t-1) + Y(t-2)/MA(t-2) + Y(t-3)/MA(t-3) + ... )

wobei Y(t-1) die Abkürzung für Y(t - 1 Jahr) ist und MA(t) den 1-Jahres gleitenden Durchschnitt von Y(t) bezeichnet.

Der in diesem Abschnitt vorgeschlagene Ansatz ist naiv, lässt sich jedoch leicht in Excel implementieren. Viele statistische Modelle finden sich in der Literatur, um Saisonalität mit komplexeren Methoden anzugehen. Z. B.: Box-Jenkins, ARMA, ARIMA, Holt-Winters…

Herausforderungen bei der Schätzung von Saisonalitätsindizes

Das hier dargestellte Saisonalitätsmodell ist ein eher naiver Ansatz, der für langfristige, gleichmäßige saisonale Zeitreihen funktioniert. Dennoch gibt es zahlreiche praktische Schwierigkeiten bei der Schätzung der Saisonalität:

1. Zeitreihen sind kurz. Die Lebensdauer der meisten Konsumgüter überschreitet in der Regel 3 oder 4 Jahre nicht. Folglich bietet die Verkaufshistorie eines gegebenen Produkts im Durchschnitt nur sehr wenige Datenpunkte, um jeden saisonalen Index (das heißt die Werte von S(t) im Jahresverlauf, vgl. den vorherigen Abschnitt) zu schätzen.
2. Zeitreihen sind verrauscht. Zufällige Marktschwankungen beeinflussen die Verkäufe und erschweren es, die Saisonalität isoliert zu betrachten.
3. Mehrere Saisonalitäten sind beteiligt. Betrachtet man die Verkäufe auf Filialebene, ist die Saisonalität des Produkts in der Regel mit der Saisonalität der Filiale verknüpft.
4. Andere Muster wie Trend oder Produktlebenszyklus beeinflussen ebenfalls Zeitreihen und führen zu verschiedenen Arten von Verzerrungen in der Schätzung.

Eine einfache – wenn auch arbeitsintensive – Methode zur Bewältigung dieser Probleme besteht darin, manuell Saisonalitätsprofile aus Aggregaten von Produkten zu erstellen, von denen bekannt ist, dass sie dasselbe saisonale Verhalten aufweisen. Die Lebensdauer des Produktaggregats ist in der Regel viel länger als die der einzelnen Produkte, was diese Schätzprobleme abmildert.

Quasi-Saisonalität

Es gibt viele Muster, die einmal im Jahr auftreten, aber nicht immer am selben Datum. Bei Lokad nennen wir diese Muster quasi-saisonal. Beispielsweise der Muttertag (der je nach Jahr an unterschiedlichen Daten liegt und außerdem zwischen Ländern variiert) und andere Feiertage wie Ramadan, Ostern und Chanukka (die ebenfalls je nach Jahr an unterschiedlichen Daten stattfinden) sind quasi-saisonal.

Diese quasi-saisonalen Ereignisse liegen außerhalb des Rahmens klassischer zyklischer Prognosemodelle, die davon ausgehen, dass die Periode des Zyklus streng konstant ist. Um mit diesen quasi-saisonalen Ereignissen umzugehen, ist eine komplexere quasi-zyklische Logik erforderlich.

Lokads Fallstrick

Nach unserer Erfahrung beeinflusst Saisonalität die überwiegende Mehrheit menschlicher Aktivitäten. Insbesondere in Zeitreihen, die die Verkäufe von Konsumgütern (sowohl Lebensmittel als auch Non-Food) darstellen, ist ein saisonaler Faktor nahezu immer vorhanden. Es kommt jedoch häufig vor, dass aufgrund der Marktgeräusche die Qualität der Schätzung der Saisonalitätsindizes zu gering ausfällt, um praktisch zur Verfeinerung der Prognosen genutzt zu werden.

Die Prognosetechnologie von Lokad behandelt sowohl Saisonalität als auch Quasi-Saisonalität von Haus aus, sodass Sie Lokad nicht explizit darüber informieren müssen – es ist bereits berücksichtigt.

Um die Probleme der begrenzten historischen Daten, die den meisten Zeitreihen im Einzelhandel oder in der Fertigung zur Verfügung stehen, zu überwinden, verwendet Lokad eine Analyse mehrerer Zeitreihen, und die Saisonalität wird nicht anhand eines einzelnen Produkts, sondern anhand vieler Produkte bewertet. Dadurch reduzieren wir das Rauschen in unserer Schätzung der Saisonalität und führen diese auch in die Prognosen ein, selbst wenn Produkte weniger als ein Jahr verkauft wurden.