Saisonnalité (Supply Chain)

Dans la supply chain, la demande - ou les ventes - d’un produit donné est censée présenter une saisonnalité lorsque les séries temporelles sous-jacentes subissent une variation cyclique prévisible en fonction du moment de l’année. La saisonnalité est l’un des motifs statistiques les plus fréquemment utilisés pour améliorer la précision des prévisions de demande.

Illustration des séries temporelles saisonnières

Le graphique ci-dessous illustre 4 séries temporelles saisonnières (cliquez pour agrandir). Les séries temporelles sont agrégées au niveau hebdomadaire sur une période de 159 semaines (environ 3 ans). Les données représentent les expéditions hebdomadaires de 4 produits distincts à partir de l’entrepôt d’un grand détaillant européen.

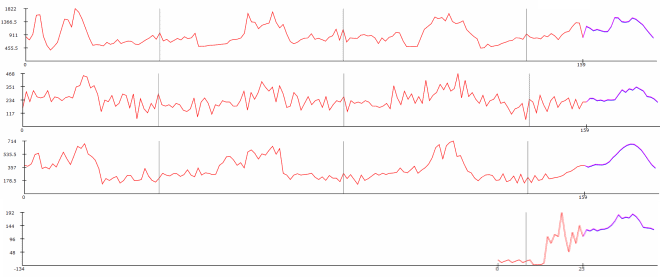
Le premier jour de l’année (le 1er janvier) est marqué par un repère vertical gris. Les données historiques apparaissent en rouge tandis que la prévision de Lokad est affichée en violet. La saisonnalité peut être observée visuellement par la similarité des motifs d’une année à l’autre ; utilisez les repères gris comme références.

Modèle de base pour la décomposition saisonnière

Soit Y(t) la demande au temps t. Nous décomposons la demande Y(t) en deux composantes : S(t), une fonction strictement cyclique, et Z(t), le complément non saisonnier. Cela donne :

Y(t) = S(t) * Z(t) où S(t + 1 an) = S(t)

Si une telle fonction S(t) peut être estimée, alors le processus de prévision se déroule typiquement en trois étapes :

• Calculer la série temporelle désaisonnalisée comme Z(t) = Y(t) / S(t).
• Produire la prévision sur la série temporelle Z(t), éventuellement par moyenne mobile.
• Réappliquer ensuite les indices de saisonnalité à la prévision.

Pour revenir au problème initial d’estimation des indices de saisonnalité S(t), en supposant qu’il n’y ait pas de tendance (entre autres), S(t) peut être estimée avec :

S(t) = MOYENNE( Y(t-1)/MA(t-1) + Y(t-2)/MA(t-2) + Y(t-3)/MA(t-3) + ... )

où Y(t-1) est l’abréviation de Y(t - 1 an) et MA(t) la moyenne mobile sur 1 an de Y(t).

L’approche proposée dans cette section est naïve, mais peut être facilement mise en œuvre dans Excel. De nombreux modèles statistiques peuvent être trouvés dans la littérature pour aborder la saisonnalité avec des méthodes plus compliquées. Ex : Box-Jenkins, ARMA, ARIMA, Holt-Winters…

Défis dans l’estimation des indices de saisonnalité

Le modèle de saisonnalité illustré ci-dessus est une approche assez naïve qui fonctionne pour des séries temporelles saisonnières longues et régulières. Pourtant, il existe de multiples difficultés pratiques lors de l’estimation de la saisonnalité :

1. Les séries temporelles sont courtes. La durée de vie de la plupart des biens de consommation n’excède pas 3 ou 4 ans. En conséquence, pour un produit donné, l’historique des ventes offre en moyenne très peu de points dans le passé pour estimer chaque indice de saisonnalité (c’est-à-dire les valeurs de S(t) au cours de l’année, cf. la section précédente).
2. Les séries temporelles sont bruyantes. Les fluctuations aléatoires du marché impactent les ventes et rendent la saisonnalité plus difficile à isoler.
3. Plusieurs saisonnalités sont impliquées. Lorsqu’on examine les ventes au niveau du magasin, la saisonnalité du produit lui-même est généralement entremêlée avec la saisonnalité du magasin.
4. D’autres motifs tels que la tendance ou le cycle de vie du produit impactent également les séries temporelles, introduisant divers types de biais dans l’estimation.

Une méthode simple - quoique nécessitant beaucoup de main-d’œuvre - pour aborder ces problèmes consiste à créer manuellement des profils de saisonnalité à partir d’agrégats de produits reconnus pour avoir le même comportement saisonnier. La durée de vie de l’agrégat de produits est généralement bien plus longue que celle des produits individuels, ce qui atténue ces problèmes d’estimation.

Quasi-saisonnalité

Il existe de nombreux motifs qui se produisent une fois par an mais pas toujours à la même date. Chez Lokad, nous appelons ces motifs quasi-saisonniers. Par exemple, la fête des Mères (qui tombe à des dates différentes selon l’année et varie également d’un pays à l’autre) et d’autres fêtes comme le Ramadan, Pâques et Hanoucca (qui tombent à des dates différentes selon l’année) sont quasi-saisonniers.

Ces événements quasi-saisonniers dépassent le cadre des modèles de prévision cyclique classiques qui supposent que la période du cycle est strictement constante. Pour traiter ces événements quasi-saisonniers, une logique quasi-cyclique plus complexe est requise.

Le piège de Lokad

D’après notre expérience, la saisonnalité impacte la grande majorité des activités humaines. En particulier, dans les séries temporelles représentant les ventes de biens de consommation (alimentaires et non alimentaires), un facteur saisonnier est presque toujours présent. Cependant, il arrive fréquemment qu’en raison du bruit du marché, la qualité de l’estimation des indices de saisonnalité se révèle trop faible pour être pratiquement utile afin d’affiner les prévisions.

La technologie de prévision de Lokad gère nativement la saisonnalité et la quasi-saisonnalité, vous n’avez donc pas à les indiquer à Lokad, c’est déjà pris en charge.

Afin de surmonter les problèmes posés par la profondeur historique limitée disponible pour la plupart des séries temporelles dans le commerce de détail ou la fabrication, Lokad utilise l’analyse de multiples séries temporelles et la saisonnalité est évaluée non pas sur un seul produit, mais en examinant de nombreux produits. Ce faisant, nous réduisons le bruit dans notre estimation de la saisonnalité, tout en introduisant la saisonnalité dans les prévisions même lorsque les produits ont été vendus pendant moins d’un an.