Séries temporelles (Supply Chain)

Les séries temporelles sont l’un des outils mathématiques les plus basiques et polyvalents utilisés en entreprise. Tout simplement, une série temporelle se compose d’une série de points de données indexés dans le temps. Une série temporelle peut ainsi modéliser n’importe quoi, de l’évolution des ventes d’une entreprise à celle des prix de leurs produits, sur une base annuelle, mensuelle, quotidienne ou même horaire. Les séries temporelles sont particulièrement intuitives, ce qui les rend idéales pour décrire, visualiser, modéliser et enfin prévoir un certain nombre de variables.

Statistiques descriptives avec les séries temporelles

La principale utilisation des séries temporelles est descriptive. Elles peuvent condenser une grande quantité d’informations dans un seul graphique ou tableau. Cependant, du fait de leur intuitivité, il est facile de les simplifier à l’excès ou de les mal interpréter. Une source d’interprétation erronée est l’agrégation temporelle utilisée par la série. Les mois de notre calendrier constituent une manière quelque peu arbitraire de diviser le temps, et il ne faut pas se faire l’illusion que ces mois sont homogènes d’un point de vue commercial. Un nombre inégal de jours et de week-ends dans un mois peut fournir une explication à ce qui pourrait apparaître au premier abord comme des écarts dans les données. D’autres phénomènes expliquent la saisonnalité dans la variation des données. Les jours fériés, tels que Noël ou Black Friday, provoquent systématiquement des pics de ventes, tout comme les jours de paie en début de mois. Cependant, une telle cyclicité ne correspond pas nécessairement à notre calendrier. Des traditions comme le Ramadan ou le Nouvel An chinois provoquent des variations cycliques dans les données, même si le cycle n’est ni mensuel ni annuel. De plus, il faut se méfier de tirer des conclusions hâtives à partir des séries temporelles ou d’établir des corrélations trop simples entre les graphiques. Il est donc important de garder à l’esprit ce qui distingue une variable d’une autre (les ventes par rapport à la demande ou aux bénéfices).

Visualiser les séries temporelles

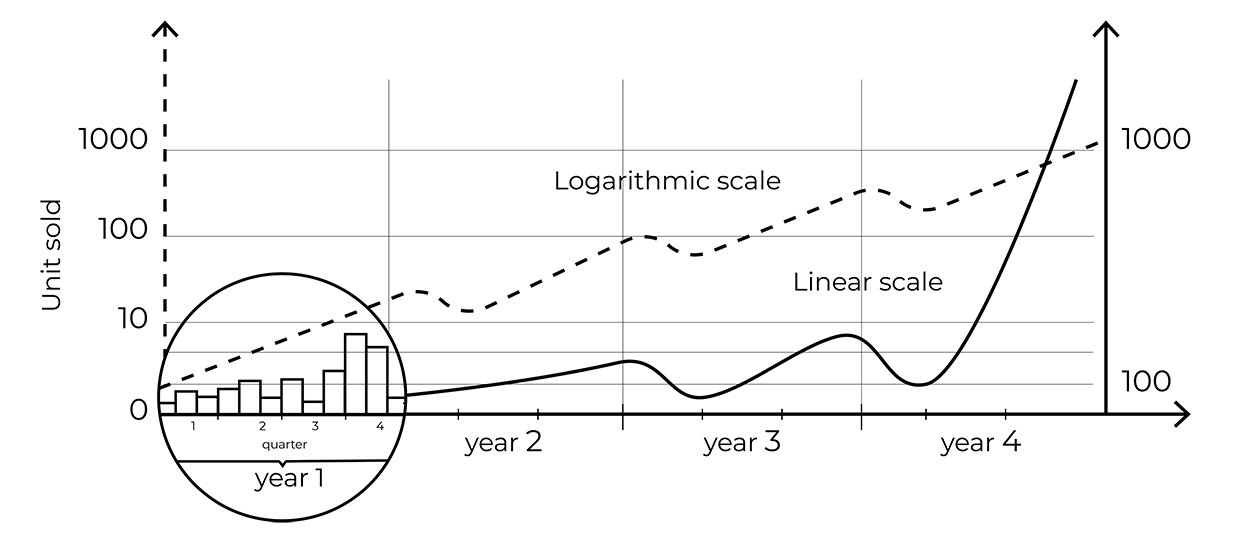
Les séries temporelles sont également souvent utilisées pour lire et visualiser des données, ainsi que pour comparer différentes séries. Encore une fois, les pièges de tels graphiques résident dans leur apparente simplicité. Différentes techniques de représentation peuvent donc être employées pour offrir la meilleure visualisation possible des données. Par exemple, relier les points de données par des lignes donne une impression de continuité. Cela peut être utile pour représenter, par exemple, l’évolution horaire des cours des actions.

Cependant, dans le cas de données particulièrement discontinues, un graphique en compartiments peut être plus approprié.

Lors de la lecture d’une série temporelle, il faut aussi prêter une grande attention à l’axe des x. Certains graphiques se concentrent sur de petits intervalles de valeurs afin de mettre en avant les variations des données, avec le risque que ces variations soient surestimées. D’autres phénomènes, tels que la croissance exponentielle, sont également mal représentés par une échelle linéaire sur l’axe des x. On peut donc choisir d’utiliser une échelle logarithmique pour que les premiers stades de croissance soient perçus aussi clairement que les stades ultérieurs.

Modélisation et prévision

Les séries temporelles sont fréquemment utilisées pour appuyer des modèles statistiques. L’objectif de ces modèles est double : expliquer le passé et prédire l’avenir. Dans la supply chain, prévoir la demande future est nécessaire pour déterminer les commandes d’achat et de production et pour minimiser les risques de surstockage. Il est courant de distinguer, au sein d’une série temporelle, un niveau primaire appelé la ligne de base, une évolution à long terme appelée la tendance, des variations cycliques ou périodiques appelées saisonnalité, et d’autres variations aléatoires que nous appelons bruit. Cela permet de distinguer les variations de données liées à des cycles réguliers d’une tendance sous-jacente à la baisse ou à la hausse. Ces schémas constituent la base des prévisions économiques.

Il existe trois principaux types de prévisions, chacun servant à des fins différentes.

• Les prévisions ponctuelles ont pour objectif de fournir la « meilleure » valeur future d’une variable selon une métrique d’erreur spécifiée. C’est le cas, par exemple, d’une prévision météo qui, pour chaque jour, prédit une valeur unique de température. Une prévision ponctuelle ne vise pas à représenter fidèlement l’évolution de cette variable (le lecteur sait pertinemment que la température est susceptible de varier autour de la valeur prédite), mais sert d’indication utile et constitue une base solide pour ses choix futurs.
• Les prévisions probabilistes fournissent l’ensemble des distributions de probabilité de la valeur future. Les intervalles de confiance sont fréquemment utilisés pour visualiser ces prévisions. Ces prévisions peuvent, par exemple, s’avérer utiles à des fins spéculatives.
• Les prévisions génératives font apparaître l’évolution de la variable comme « naturelle » ou « plausible », permettant ainsi une certaine contingence et une évolution aléatoire. Cette « perspective générative » peut être utile lors de l’exécution de simulations.

L’écosystème logiciel autour des séries temporelles

De nombreux types de logiciels sont désormais utilisés afin de prendre en compte les complexités liées aux séries temporelles et de fournir des modèles ou des prévisions qui répondent au mieux aux attentes des utilisateurs. On peut trouver des bases de données, des outils open-source, et même des langages de programmation exclusivement dédiés aux séries temporelles. De nombreuses méthodes de prévision ont également été développées. Par exemple, certains logiciels estiment simplement les valeurs futures à l’aide d’une moyenne mobile, tandis que d’autres optent pour le lissage exponentiel, signifiant que le poids des valeurs passées diminue de façon exponentielle à mesure qu’elles s’éloignent dans le temps.

Les séries temporelles constituent ainsi une abstraction particulièrement polyvalente et un outil statistique de base. Cependant, leur apparente simplicité peut être trompeuse. Un certain nombre de facteurs peuvent soit altérer la manière dont les données sont présentées, soit expliquer des variations notables dans les données. Il est donc essentiel de savoir comment les données sont collectées et d’être conscient des facteurs susmentionnés.