Priorisierte Lagerauffüllung in Excel mit probabilistischen Vorhersagen
Unsicherheit ist ein unabdingbarer Aspekt der Prognose. Dennoch entstand im 20. Jahrhundert die statistische Prognose mit der Hoffnung, dass bei adäquaten mathematischen Modellen die Unsicherheit eliminiert werden könnte. Infolgedessen spielten frühe supply chain Theorien die Unsicherheit herunter oder wiesen sie zurück, da erwartet wurde, dass neuere oder bessere Prognosen sie entweder beseitigen oder, falls nicht, unbedeutend machen würden. Obwohl gut gemeint, waren diese Ansätze fehlerhaft, denn auch nach einem Jahrhundert statistischer Modellierung bleibt die Unsicherheit hartnäckig irreduzibel. Im Jahr 2012 ebnete Lokad den Weg für einen alternativen supply chain perspective, der die Unsicherheit annimmt und quantifiziert. Dieser Ansatz nutzt probabilistische Vorhersagen anstelle der klassischen Punkt-Zeitreihen-Prognosen. In diesem Leitfaden und der begleitenden Microsoft Excel-Tabelle wenden wir probabilistische Vorhersagen auf das Problem der Lagerauffüllung an. Dieser Ansatz führt zu einer priorisierten Lagerauffüllungspolitik, die hier in Excel demonstriert wird. Unser Ziel ist zweifach: Erstens, diesen Ansatz einem Publikum näherzubringen, das sich mit fortgeschritteneren Softwaretools möglicherweise weniger wohlfühlt; und zweitens, zu zeigen, dass das Akzeptieren von Unsicherheit mehr eine bestimmte Denkweise als hochentwickelte Werkzeuge erfordert.
Herunterladen: probabilistic-inventory-replenishment.xlsx
1. Das Lagerauffüllungsproblem
Das Lagerauffüllungsproblem konzentriert sich darauf, die beste Einkaufsliste zu identifizieren – eine, die die zentralen finanziellen Einschränkungen und Ziele des Unternehmens berücksichtigt. Die Methode zur Erstellung einer solchen Liste sollte unabhängig von Budgetbeschränkungen gleichermaßen funktionieren, da sie darauf abzielt, die Kapitalrendite für jeden investierten Dollar zu maximieren. Das Problem besteht darin, dass alle SKUs um dieselben Mittel konkurrieren, sodass der finanzielle Ertrag der Lagerung einer beliebigen Einheit eines SKUs im Kontext aller zusätzlichen Einheiten jedes SKUs quantifiziert und bewertet werden muss.
1.1 Die priorisierte Lagerauffüllungslösung
Der Prozess der Rangordnung des Inventars, wie oben beschrieben, erfordert eine mikroskopische Perspektive. Um den Ertrag des Hinzufügens einer beliebigen Einheit eines SKUs zu einer Einkaufsliste vergleichen zu können, sind mehrere Faktoren zu berücksichtigen – namentlich die Wahrscheinlichkeit des Verkaufs, wie sie durch eine probabilistische Nachfrageprognose bereitgestellt wird, und die wirtschaftlichen Treiber, etwa Bruttogewinnmarge und Einkaufspreis. Jede betrachtete Menge muss zudem in Bezug auf interne und externe Einschränkungen (wie begrenzte Lagerkapazitäten, Losmultiplikatoren und MOQs/MOVs usw.) abgewogen werden. Randfälle, wie wenn zwei (oder mehr) Einheiten den gleichen erwarteten Ertrag aufweisen, müssen in einer Lagerauffüllungspolitik durch die Bewertung der relativen Wichtigkeit jedes Produkts berücksichtigt werden. SKUs sollten nicht isoliert, sondern in Bündeln betrachtet werden. Einige SKUs – auch wenn sie isoliert betrachtet geringere Gewinnmargen aufweisen (wie Milch) – sind wichtiger, da sie den Verkauf von Produkten mit hoher Marge ermöglichen. Somit stellt der finanzielle Anreiz, Service Levels eines Produkts mit geringerer Marge – eines Produkts, das andere Verkäufe ermöglicht – aufrechtzuerhalten, einen weiteren Treiber dar. Ein priorisierter Lagerauffüllungsansatz (PIR), der probabilistische Prognosen als Input nutzt, berücksichtigt all diese Faktoren.
Kurz gesagt, lässt sich die PIR-Lösung in drei Schritte zusammenfassen:
1. Erstelle eine probabilistische Nachfrageprognose.
2. Liste alle machbaren Einkaufsgrößen auf.
3. Ordne alle machbaren Einkaufsgrößen nach den wirtschaftlichen Treibern.
1.2 Priorisierte Lagerauffüllung in Excel
Unter Verwendung finanzieller Daten für einen fiktiven Laden, einschließlich der im vorigen Abschnitt genannten wirtschaftlichen Treiber, modelliert diese Excel-Tabelle die Lagerauffüllungspolitik für drei SKUs (Stifte, Tastaturen und Bücherregale)1. Die finanziellen Konsequenzen jeder zusätzlichen Einheit eines SKUs (falls bestellt) und die Wahrscheinlichkeit, sie zu verkaufen, werden im Charts-Sheet veranschaulicht (siehe Abbildung 1). Die Diagramme und Charts aktualisieren sich abhängig von den Eingaben und den Modellannahmen (z. B. Anfangsbestände, Kauf- und Verkaufspreise usw.) im Control Tower-Sheet (Abbildung 2). Eine detaillierte Liste machbarer Entscheidungsoptionen wird im Micro purchasing decisions-Sheet (Abbildung 3) basierend auf den Schlüsselfaktoren generiert. Diese Eingaben stammen aus den probabilistischen Nachfrageprognosen des Distribution generators-Sheets (Abbildung 4) sowie aus dem Control Tower-Sheet. Schließlich wird eine Tabelle mit priorisierten Lagerauffüllungsentscheidungen zusammengestellt und hinsichtlich der erwarteten Kapitalrendite sortiert (siehe Ranked purchasing decisions-Sheet in Abbildung 5).
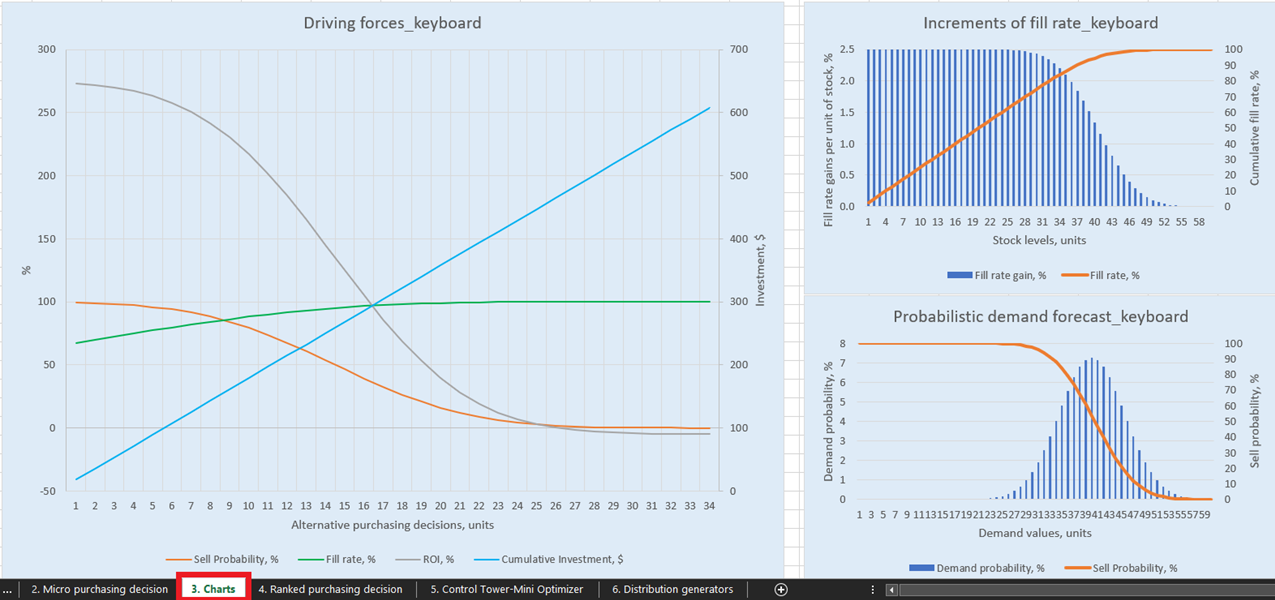
Abbildung 1. Ansicht von “Driving forces keyboard” in Charts, Position rot hervorgehoben.
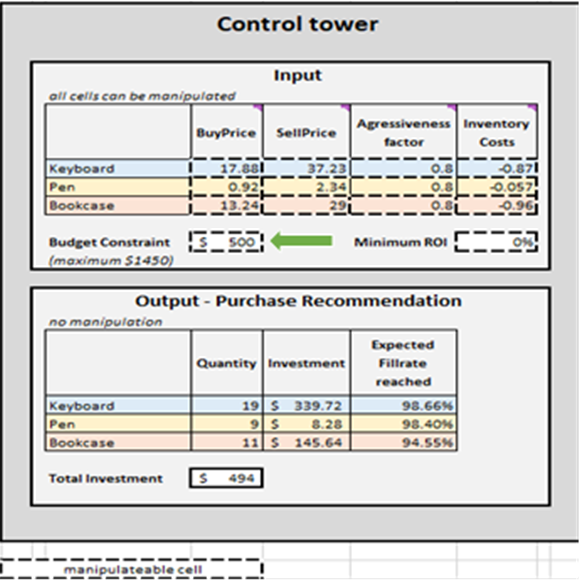
Abbildung 2. Ansicht des “Control Tower” im Control Tower – Mini Optimizer (Sheet 5). Man kann den “Budget Constraint” auf einen beliebigen Wert zwischen $0 und $1450 ändern (siehe grüner Pfeil).
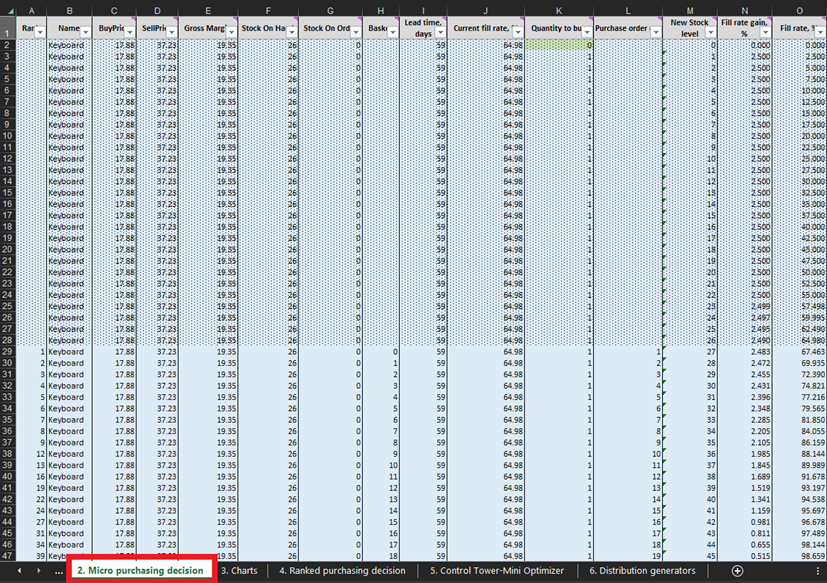
Abbildung 3. Platzierung der Micro purchasing decisions in Excel, farblich in Rot hervorgehoben. Die Zeilen, die durch bedingte, gestrichelte Formatierung markiert sind, stellen vergangene Daten dar (bis einschließlich Zeile 28 im obigen Bild). Diese Informationen repräsentieren frühere Einkaufsentscheidungen. Wir betrachten ausschließlich alles, was unterhalb dieser Formatierung liegt. Die gleiche gestrichelte Formatierung gilt für die Daten von Stiften und Bücherregalen.
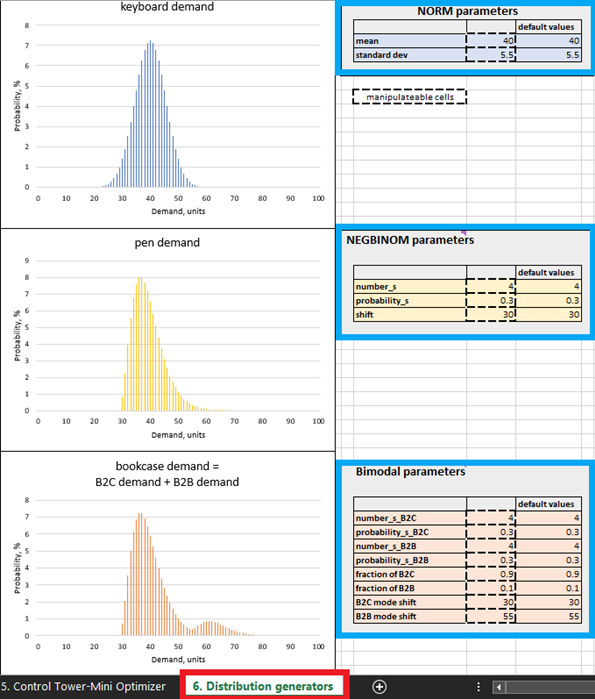
Abbildung 4. Platzierung der Distribution generators in Excel, farblich in Rot hervorgehoben. Produkt-Steuerungspanels sind in Blau markiert. Die Zellen mit gestrichelten Konturen können verändert werden.
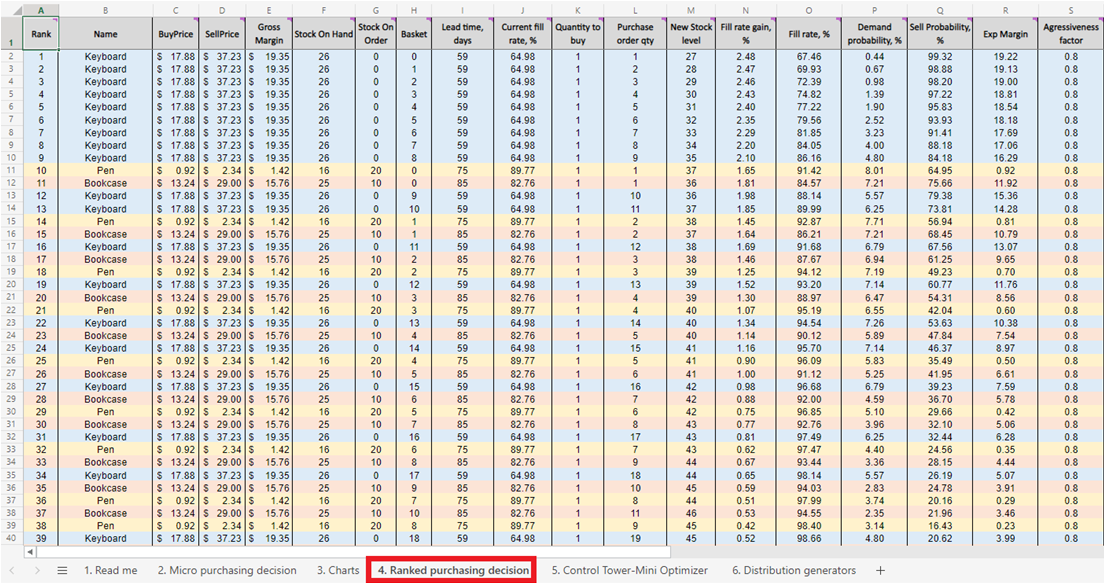
Abbildung 5. Eine priorisierte Liste der Lagerauffüllungsentscheidungen im Rahmen der Micro purchasing decisions, zu finden im Sheet 4.
2. Probabilistische Nachfrageprognose
Im vorliegenden Kontext ist eine probabilistische Prognose die Menge aller wahrscheinlichen zukünftigen Nachfragewerte und deren jeweiliger Wahrscheinlichkeiten. Sie fasst die inhärente Unsicherheit der zukünftigen Nachfrage zusammen und kann für jeden beliebigen Zeitraum erstellt werden. Wie bei einer herkömmlichen Zeitreihenprognose wird ein einzelner, am wahrscheinlichsten auftretender Nachfragewert identifiziert (die weißen Punkte in Abbildung 6) sowie eine Trendlinie (die graue Linie, die die weißen Punkte verbindet). Eine probabilistische Prognose integriert jedoch die Unsicherheit, indem sie alle möglichen (wenn auch nicht gleich wahrscheinlichen) Nachfragewerte einbezieht. Dieser Ansatz zeigt sich in Abbildung 6, wo unterschiedliche Vertrauensintervalle Nachfragewerte mit verschiedenen Wahrscheinlichkeiten darstellen.
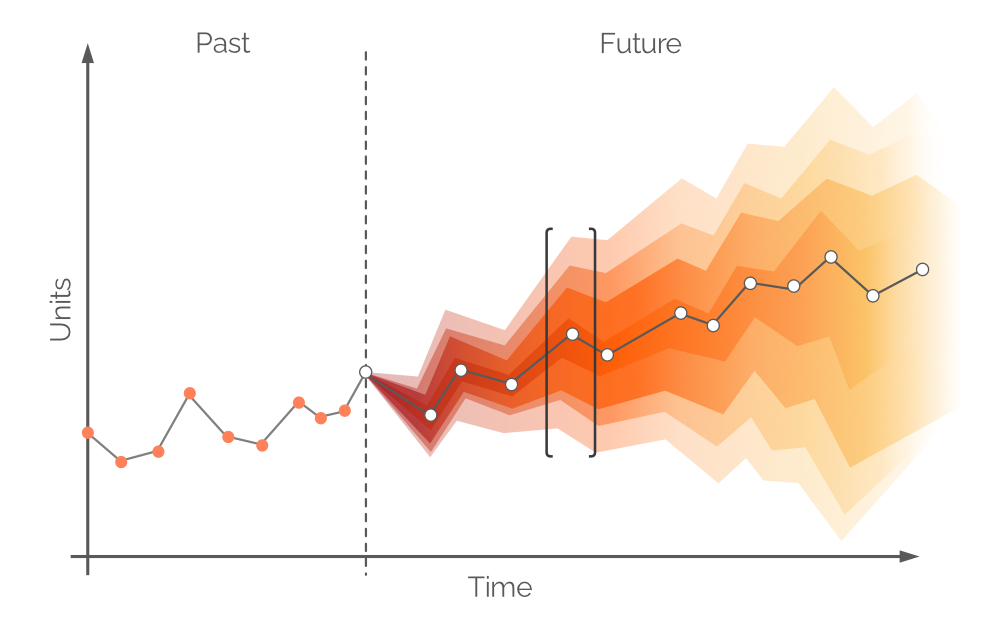
Abbildung 6. Eine probabilistische Prognose (Nachfrage auf der y-Achse; Zeit auf der x-Achse). Die gestrichelte, vertikale graue Linie zeigt den aktuellen Moment (“jetzt”) an. Die Zeit wird in Tagen gemessen, wobei dies jedem gewünschten Intervall entsprechen könnte. Der in schwarzen Klammern dargestellte Bereich wird später erläutert.
Die weißen Punkte in Abbildung 6 repräsentieren die am wahrscheinlichsten auftretenden Nachfragewerte zu festen zukünftigen Intervallen. Ein begleitendes Farbband entspricht einem Spektrum alternativer zukünftiger Nachfragewerte – eine farbige Wahrscheinlichkeitsverteilung. Diese Farbe wird entlang der vertikalen Achse immer blasser, je weiter man sich vom weißen Punkt entfernt, was die zunehmende Unsicherheit und geringere Wahrscheinlichkeit symbolisiert. Insgesamt werden die Farbbänder blasser, je weiter die Zeit fortschreitet (entlang der horizontalen Achse), da die Unsicherheit mit der Zeit zunimmt. Unabhängig von der Unsicherheit existiert jedoch stets mindestens ein Wert, der am wahrscheinlichsten ist, was sich jederzeit in den weißen Punkten widerspiegelt. Ein Beispiel für eine Wahrscheinlichkeitsverteilung zu einem einzelnen Zeitpunkt wird in Abbildung 7 illustriert.
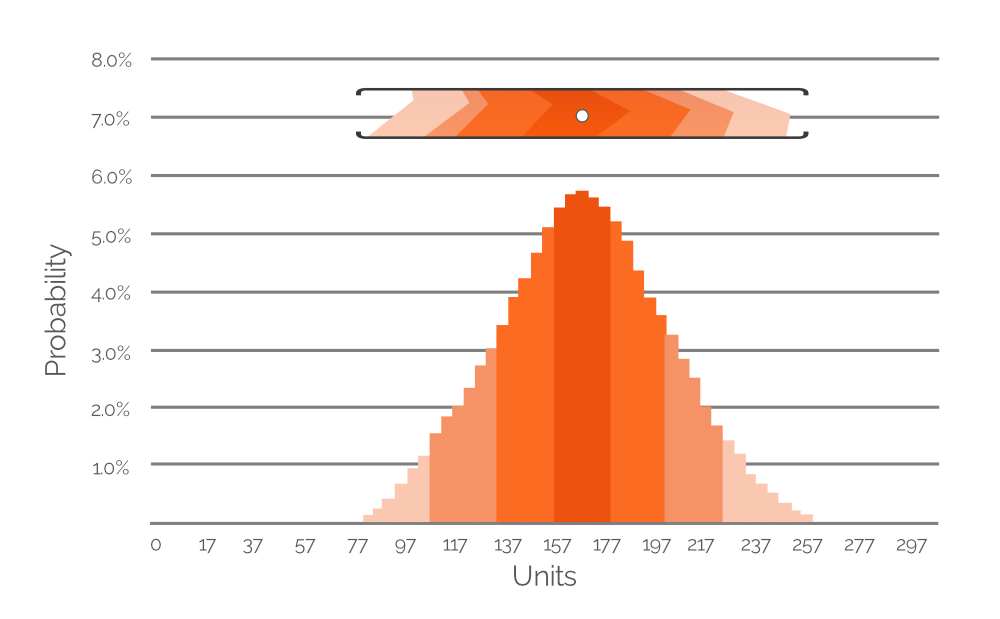
Abbildung 7. Ein Histogramm, das die Wahrscheinlichkeit mehrerer möglicher Nachfragewerte (im 20-Einheiten-Intervall) darstellt. Die y-Achse zeigt den Wahrscheinlichkeitswert; die x-Achse die Nachfrage in Einheiten. Das Histogramm bildet den in Abbildung 6 hervorgehobenen Wertebereich ab (zur Referenz beigefügt).
Abbildung 7 stellt die hervorgehobenen Daten aus Abbildung 6 als Wahrscheinlichkeits-Histogramm dar, in dem explizite numerische Werte die Wahrscheinlichkeit verschiedener Nachfragewerte angeben. Die Farbkennzeichnung bleibt erhalten, um das Verständnis zu erleichtern (denken Sie daran: Blassere Farben sind weniger wahrscheinlich, während dichtere Farben wahrscheinlicher sind). In diesem Beispiel beträgt der am wahrscheinlichsten erwartete Nachfragewert 167 Einheiten (+/-), weshalb der weiße Punkt im zugeschnittenen Wertebereich aus Abbildung 6 direkt über dem höchsten Balken des Histogramms positioniert ist. Darüber hinaus weisen wir auch extrem niedrigen und hohen Nachfragewerten Wahrscheinlichkeiten zu (etwa 80 bzw. 260 Einheiten, beide in sehr blassem Orange). Dies demonstriert den potenziellen Datenreichtum einer probabilistischen Prognose, und ähnliche Histogramme sind in der Excel-Tabelle enthalten – eines für jeden unserer SKUs (siehe Abbildung 4). Anhand dieser Histogramme (wie in Abbildung 7 oben) können Nachfragewerte (in Einheiten) mit nicht-null Wahrscheinlichkeit identifiziert und in die PIR einbezogen werden.
2.1 Der Aufbau einer probabilistischen Prognose
Obwohl es möglich ist, mit historischen Daten in Excel eine echte probabilistische Prognose zu erstellen, ist Excel vermutlich das am wenigsten geeignete Werkzeug für diesen Zweck. Die Details zum Aufbau einer produktionsreifen probabilistischen Prognose gehen über den Rahmen dieses Dokuments hinaus, weshalb aus Gründen der Einfachheit synthetische probabilistische Prognosen ausgewählt wurden. Die Parameter dieser synthetischen Prognosen können im Distribution generators-Sheet (siehe Abbildung 4) angepasst werden. Es wird jedoch empfohlen, zunächst die Standardeinstellungen zu studieren, bevor Änderungen vorgenommen werden.
In der etablierten supply chain Praxis wird die Nachfrage typischerweise als normalverteilt angesehen, was jedoch eher die Ausnahme als die Regel ist. In realen supply chains weichen die meisten SKUs von einer Normalverteilung ab. Angesichts dieser Realität haben wir bewusst drei verschiedene Verteilungsmuster ausgewählt: normal (für Tastaturen), negativ binomial (für Stifte) und bimodal (für Bücherregale – eine Mischung aus zwei negativ binomialen Mustern). Im Folgenden wird diese Annahme begründet.
Beispielsweise gehen wir davon aus, dass Bücherregale sowohl von Privatpersonen als auch von Unternehmen (z. B. Schulen) gekauft werden, weshalb wir eine bimodale Verteilung verwenden. In der Standardeinstellung für Bücherregale gibt es häufige Nachfrage von Privatpersonen, bei denen pro Kunde ein oder zwei Einheiten gekauft werden. Dies stellt den ersten Modus der Verteilung dar (siehe Abbildung 4). Unternehmen hingegen treten als weniger häufige Nachfrager auf, tätigen aber größere Bestellungen (größer als es bei Privatpersonen üblich ist). Wenn dies geschieht, addiert sich ihre Nachfrage zur durch Privatkäufe generierten Nachfrage, und der zweite Modus der Verteilung tritt auf. Dieser zweite Modus ist nach rechts verschoben (was hohe Nachfragewerte repräsentiert) und ist deutlich kleiner als der erste Modus, was widerspiegelt, dass er seltener auftritt (Abbildung 4). Unser Modell geht außerdem davon aus, dass Stifte von Privatpersonen mit gelegentlich hohem Bedarf gekauft werden (etwa von Studenten kurz vor Prüfungsterminen). Schließlich folgen die Tastaturverkäufe einem normalverteilten Muster, um der Tatsache Rechnung zu tragen, dass eine Normalverteilung gelegentlich auftritt.
Im Distribution generators-Sheet (Abbildung 4) können Nachfrageverteilungen bearbeitet werden, indem die Parameter in den veränderbaren Zellen angepasst werden. Beispielsweise führt eine Erhöhung des Mittelwerts für Tastaturen (siehe „NORM parameters“ in Abbildung 4) von 40 auf 50 dazu, dass sich die Verteilung um 10 Einheiten nach rechts verschiebt. Infolgedessen steigt die erwartete Kapitalrendite für alle Tastatureinheiten. Ebenso können die Parameter der negativ binomialen (Stifte) und bimodalen (Bücherregale) Verteilungen modifiziert werden.
Da Excel nicht die erforderliche Ausdruckskraft für diese Art von Berechnungen besitzt, beschränkt diese Demonstration die Anpassungen auf 100 Einheiten pro Produkt. Beispielsweise führt das Setzen des Tastaturmittelwerts auf 99 dazu, dass fast 50% der Nachfrageeinheiten im Micro purchasing decisions-Sheet nicht berechnet werden können.
2.2 Auswahl eines Horizonts für eine probabilistische Nachfrageprognose
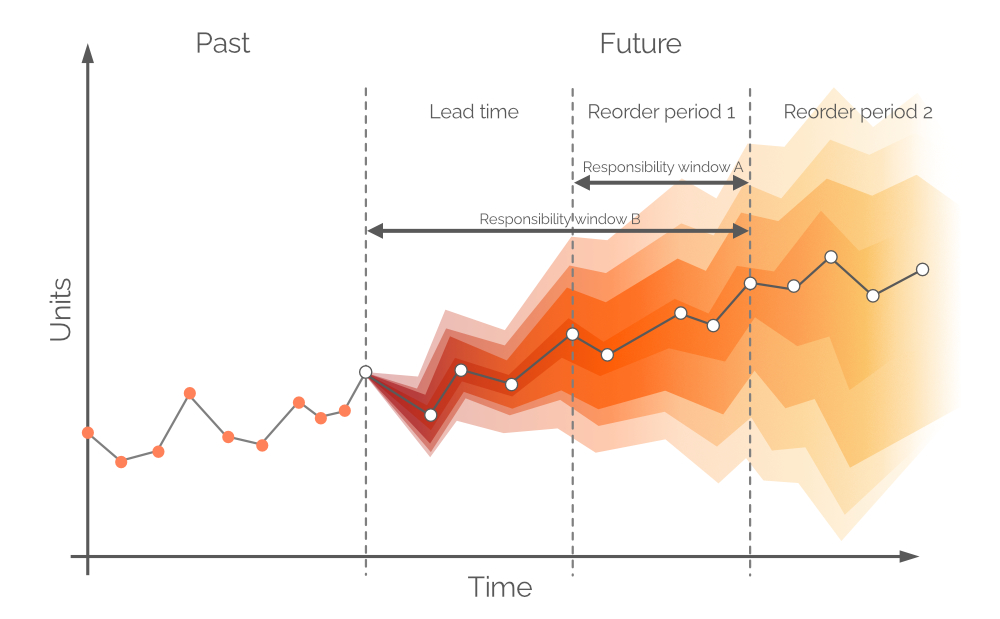
Typischerweise werden Prognosen in tägliche/wöchentliche/monatliche Intervalle unterteilt, wobei diese diskreten Perioden aus der Perspektive der Lagerauffüllung nur begrenzten Nutzen haben. Die Nachfrage über die nächste Lieferzeit kann durch heutige Einkaufsentscheidungen nicht abgedeckt werden, sofern nicht rückständiger Auftrag zugelassen ist, da alle bestellten Einheiten erst nach einem Zeitraum eintreffen, der der Lieferzeit entspricht. Daher sollte die Nachfrage durch den vorhandenen Lagerbestand sowie die bereits bestellte Ware gedeckt werden (siehe Abbildung 8), vorausgesetzt, die on order-Einheiten treffen vor der Nachfrage ein. Folglich befasst sich die probabilistische Prognose mit der Nachfrage zwischen den Nachbestellpunkten bzw. der Nachfrage während der Nachbestellperiode 1 (siehe Abbildung 9). Weiter entfernte zukünftige Nachfrage wird durch zukünftige Bestellungen abgedeckt (siehe Nachbestellperiode 2 in Abbildung 9).

Abbildung 8. Lagerbestand (Spalte F) und Bestellbestand (Spalte G), in Rot hervorgehoben, befinden sich in Mikro-Beschaffungsentscheidungen. Lieferzeit, Spalte I, ist in Blau hervorgehoben.
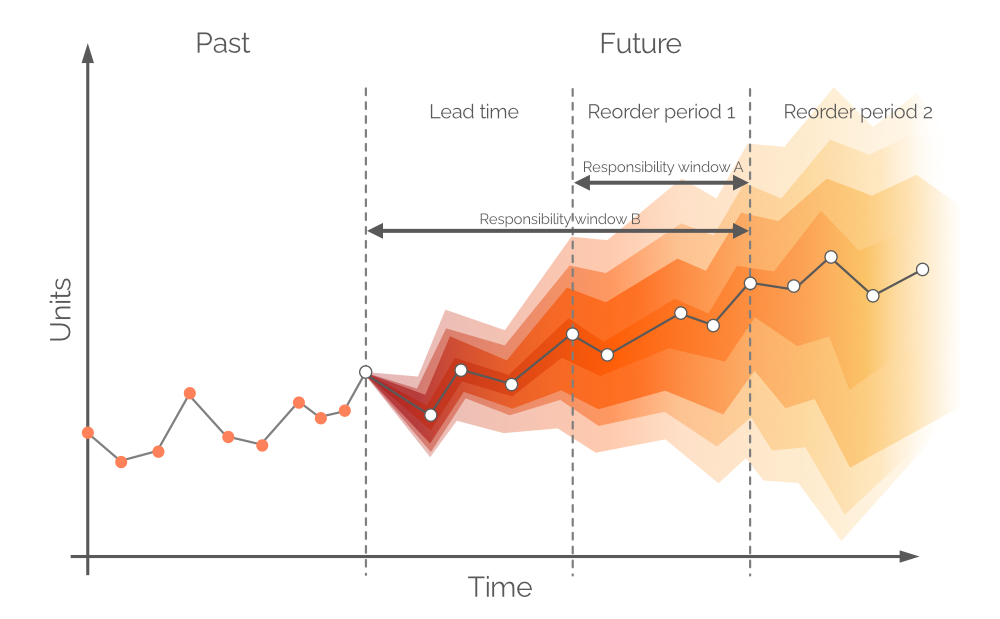
Abbildung 9. Eine visuelle Darstellung alternativer Verantwortungszeiträume. Die Nachfrage wird auf der y-Achse dargestellt, die Zeit auf der x-Achse, wobei die gestrichelte vertikale graue Linie auf der linken Seite den aktuellen Moment („jetzt“, siehe Abbildung 6) anzeigt. Die probabilistische Prognose in diesem Dokument bezieht sich auf die Nachfrage über den Horizont, der gleich Responsibility window B ist.
Theoretisch sollte die probabilistische Nachfrageprognose über einen Zeitraum erstellt werden, der Reorder period 1 entspricht – dieses Zeitfenster wird als Responsibility window A bezeichnet (siehe Abbildung 9). Um dies zu bewerkstelligen, müssten wir zukünftige Projektionen für Lagerbestand und Bestellbestand am Ende der Lieferzeit vornehmen. Allerdings ist die Nachfrage über Lieferzeit – für die bereits im vorherigen Bestellzeitraum Entscheidungen getroffen wurden – ebenfalls probabilistisch, was dazu führen würde, dass die Lagerbestände selbst Wahrscheinlichkeitsverteilungen darstellen2. Durch die Zulassung von rückständigen Aufträgen kann eine probabilistische Prognose über einen gemeinsamen Zeitraum erstellt werden (Lieferzeit plus Reorder period 1, siehe Abbildung 9, alias Responsibility window B).
Es kann angenommen werden, dass die aktuellen Bestände an Lagerbestand und Bestellbestand die Nachfrage während der Lieferzeit decken. Sollte es zu einem Fehlbestand kommen, wird jede anschließende Nachfrage durch rückständige Aufträge gedeckt. Diese rückständigen Aufträge werden durch die heute getroffenen Mikro-Beschaffungsentscheidungen bedient. Dies ermöglicht es uns, Lagerbestand und Bestellbestand als diskrete Werte zu behandeln (anstatt als zufällige)3.
3. Identifizierung praktikabler Optionen für Bestandsauffüllungsentscheidungen
In einem realen Szenario zur Bestandsauffüllung müsste man alle machbaren Entscheidungsoptionen skizzieren, da es keinen direkten Weg gibt, von einer probabilistischen Prognose zur einzig besten Entscheidung (in diesem Fall zur Bestellmenge) für jedes Produkt überzugehen. Anstelle einer einzigen perfekten Wahl stellt ein probabilistischer Ansatz eine Bandbreite möglicher Entscheidungen dar, die unter dem Gesichtspunkt der Machbarkeit berücksichtigt werden müssen.
Machbarkeit hat hier in der umgangssprachlichen Bedeutung, dass eine Entscheidung sofort handlungsfähig ist; sie kann so umgesetzt werden, wie sie ist, ohne weitere Berechnungen oder Kontrollen. Beispielsweise ist eine Entscheidung „machbar“, wenn sie profitabel ist und alle unsere Einschränkungen erfüllt (z. B. MOQs, EOQs, Losgrößen, vollständige Containerlieferungen und jede andere Einschränkung, die in unserer supply chain existieren mag)4.
In jeder Zeile des Blattes Mikro-Beschaffungsentscheidungen (Abbildungen 3 und 10) müssen wir in Erwägung ziehen, eine weitere Einheit Lagerbestand zu unserer Bestellung für ein bestimmtes Produkt hinzuzufügen5. Unsere „Gegenwart“ (bzw. Tag 1 dieses Experiments) beginnt in Zeile 29, die den aktuellen Lagerbestand anzeigt. Dieser wird als Summe von Lagerbestand und Bestellbestand berechnet. Wenn wir uns entscheiden, eine Einheit zur Bestellung hinzuzufügen, wird die gesamte Bestellmenge in Spalte L als Summe aller bisher für den Einkauf berücksichtigten Einheiten berechnet (Siehe Anmerkungen in Abbildung 10).
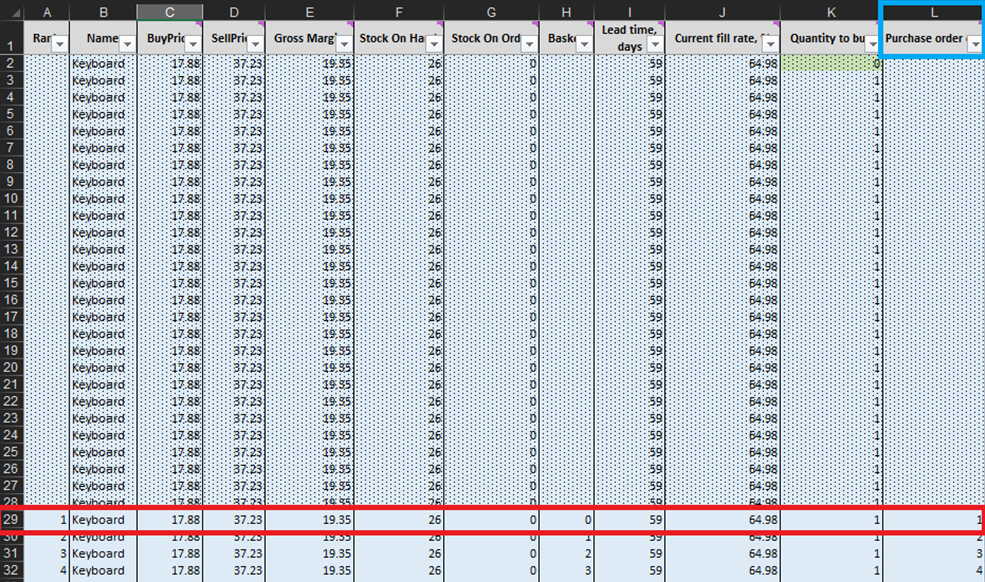
Abbildung 10. Blick innerhalb des Blattes _Mikro-Beschaffungsentscheidungen_. Zeile 29, in Rot hervorgehoben, markiert den Beginn unseres Experiments (für Tastaturen). Die Spalte für die Bestellmenge ist in Blau hervorgehoben. Dasselbe Prinzip gilt für Zeile 140 (für Bestellungen von Stiften) und Zeile 240 (für Bestellungen von Bücherregalen).
Sobald diese machbaren Bestandsentscheidungen identifiziert wurden, berechnen und bewerten wir den wirtschaftlichen Ertrag jedes möglichen Einkaufs. Beachten Sie, dass wir den Einkaufs-Ertrag für Einheiten, die derzeit entweder als Lagerbestand oder als Bestellbestand geführt werden (Spalten F und G in Abbildung 10), nicht auswerten. Da diese Einheiten bereits gekauft wurden, wurde der theoretische wirtschaftliche Ertrag zu einem früheren Zeitpunkt bestimmt (und bewertet). Beispielsweise gibt es in den Tastaturdaten in Abbildung 10 derzeit 26 Einheiten auf Lager. Daher beginnen wir die Berechnungen in Zeile 29 und prüfen, ob wir unsere erste zusätzliche Einheit bestellen sollten (was den Lagerbestand von 26 auf 27 Einheiten erhöhen würde).
3.1 Bewertung machbarer Einkaufsentscheidungen
Um für jedes Produkt die beste Bestellmenge zu wählen, ist es notwendig, den erwarteten monetären Ertrag auf Einheitenebene für jede machbare Menge für jedes Produkt zu berechnen (unter Berücksichtigung der unsicheren Zukunft, die durch die probabilistische Prognose dargestellt wird). Dies ist ein Erwartungswertkonzept, das an die feinste Ebene der Bestands-Entscheidungsfindung angepasst wurde.
In der Realität sollte jede Art von wirtschaftlichem Treiber berücksichtigt werden, wenn versucht wird, den erwarteten Ertrag für jede machbare Entscheidung zu berechnen6. Für diese Demonstration betrachten wir folgende Faktoren:
- Verkaufspreis: Wie viel wir den Kunden für das Produkt berechnen.
- Lagerkosten: Wie viel es uns kostet, das Produkt zu lagern.
- Einkaufspreis: Wie viel es uns kostet, das Produkt von unserem Lieferanten/Großhändler zu beziehen.
- Fehlbestandabdeckung: Wird im Folgenden detailliert erläutert, da es sich um einen weniger bekannten, aber dennoch wichtigen Treiber handelt7.
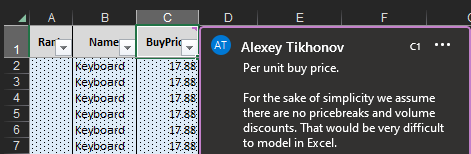
Abbildung 11. Erklärhinweis zu Einkaufspreis, einsehbar durch Mouseover über die Spaltenüberschrift. Für jede Spalte in jedem Blatt des Excel-Dokuments gibt es eine Definition.
Fehlbestandabdeckung stellt einen finanziellen Anreiz dar, eine Einheit eines Produkts auf Lager zu halten, jedoch nicht mit dem expliziten Ziel, es zu verkaufen. Dieser wirtschaftliche Treiber wird verwendet, um die relative Wichtigkeit eines Produkts im Vergleich zu anderen zu modellieren. Er motiviert dazu, ein Fehlbestandsereignis für Produkte zu vermeiden, die aufgrund ihrer direkten Margenbeiträge als weniger wichtig angesehen werden könnten, da diese Produkte auf indirekte Weise erheblich zu den Gewinnspannen beitragen können. Insofern ähnelt er eher einem Reward-Treiber8. Obwohl dieser Treiber unscharf ist, ist es entscheidend, alle kritischen Produkte zu identifizieren (auch solche, die keine direkten Margenbeiträge liefern).
3.2 Berechnung des Scores jeder machbaren Entscheidung
Die gesamte wirtschaftliche Konsequenz (oder Einkaufs-Ertrag) einer Bestandsauffüllungsentscheidung ist die Summe aller wirtschaftlichen Treiber, einschließlich erwarteter Marge, erwarteter Lagerhaltungskosten und Fehlbestandabdeckung (im Folgenden detailliert definiert). Lagerkosten sind in diese Berechnungen als negativer Treiber einbezogen, der als Gegenkraft zur Ausbalancierung unserer Bestandsauffüllungsentscheidungen wirkt.
Im Folgenden wird eine Analyse der wirtschaftlichen Implikationen der Formeln in jeder Spalte vorgestellt, wobei Zeile 29 des Blattes Mikro-Beschaffungsentscheidungen als Beispiel herangezogen wird (siehe Abbildung 12).

Abbildung 12. Aufschlüsselung der Treiber in den wichtigen Spalten, unter Verwendung von Zeile 29 des Blattes Mikro-Beschaffungsentscheidungen (Excel-Blatt 2). Bestimmte Spalten wurden der Übersichtlichkeit halber ausgeblendet.
Um den erwarteten Ertrag für jede Entscheidung zu berechnen, benötigen wir folgende Treiber:
Bruttomarge (Spalte E) = Verkaufspreis – Einkaufspreis.
Verkaufswahrscheinlichkeit (Spalte Q) = Siehe Formel im Blatt9.
Nicht-Verkaufswahrscheinlichkeit (keine Spalte) = 100 % - Verkaufswahrscheinlichkeit
Erwartete Marge (Spalte R) = Bruttomarge * Verkaufswahrscheinlichkeit / 100.
Aggressivitätsfaktor (Spalte S) = Reicht von 0 bis 1. Für dieses Tool wurde 0,8 gewählt.
Fehlbestandabdeckung (Spalte T) = Verkaufspreis * Aggressivitätsfaktor * Verkaufswahrscheinlichkeit
Lagerkosten (Spalte U)
Erwartete Lagerhaltungskosten (Spalte V) = Lagerkosten * Nicht-Verkaufswahrscheinlichkeit10.
Mithilfe der obigen Daten wird der Einkaufs-Ertrag für jede mikroökonomische Bestandsentscheidung (jede Einheit eines Produkts) wie folgt berechnet:
Einkaufs-Ertrag (Spalte W) = Erwartete Marge + Fehlbestandabdeckung + Erwartete Lagerhaltungskosten.
Sobald wir die Schätzung des Einkaufs-Ertrags haben, können wir den finalen Score berechnen, den wir später zur Rangordnung aller in Betracht gezogenen Entscheidungen verwenden.
Score (Spalte Y) = Einkaufs-Ertrag / Investment (Spalte X)11.
Da Fehlbestandabdeckung ein unscharfer Treiber ist, der sowohl direkte als auch indirekte Erträge berücksichtigt, spiegelt der Einkaufs-Ertrag nicht isoliert den erwarteten Ertrag einer Bestandsentscheidung wider. Möchte man diese Art von Ertrag berechnen, würde man Fehlbestandabdeckung aus dieser Formel ausschließen12.
4. Rangordnung machbarer Bestandsauffüllungsentscheidungen
Sobald wir den Score für jede machbare Einkaufsentscheidung (für jedes Produkt) haben, wird eine Liste erstellt und in absteigender Reihenfolge (von höchstem zu niedrigstem) in den Rangierten Einkaufsentscheidungen sortiert (siehe Abbildung 13). Jede machbare Bestandsentscheidung wird hinsichtlich eines positiven ROI % bewertet. Jedem Entscheidungsvorschlag wird zudem ein ordinales Ranking (1., 2., 3. usw.) zugeordnet (siehe Spalte A in derselben Abbildung).
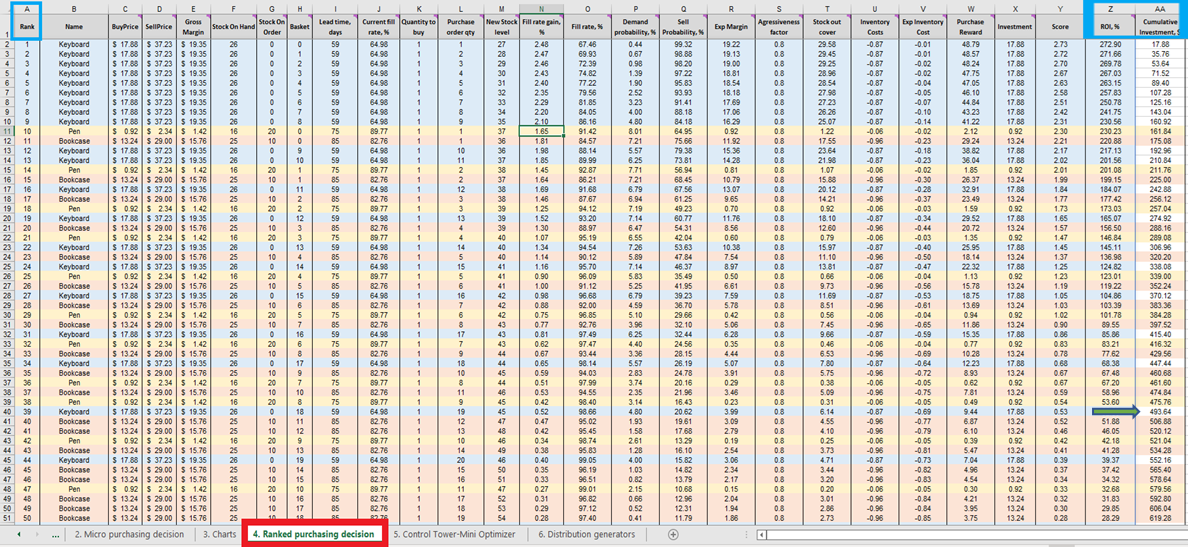
Abbildung 13. Der Bereich der *Rangierten Einkaufsentscheidungen* ist in Rot hervorgehoben. Die Spalten A, Z und AA sind in Blau markiert. Zelle 40 (der Grenzwert für ein Budget von 500 $, Standard im Spreadsheet) wird durch den grünen Pfeil angezeigt.
Rangierte Einkaufsentscheidungen zeigen farblich codierte Zeilen für jedes Produkt (Tastaturen, Stifte und Bücherregale), um zu demonstrieren, wie sich die Entscheidung, eine zusätzliche Einheit eines beliebigen Produkts hinzuzufügen, mit jeder weiteren zusätzlichen Einheit jedes anderen Produkts verhält. Jede dieser Bestandsentscheidungen beeinflusst kollektiv den ROI. Schließlich wird ein kumulativer Investitionswert berechnet (Spalte AA, Abbildung 13). Dieser kann herangezogen werden, um anzugeben, wo man die Bestellentscheidungen im Hinblick auf die Budgetbeschränkungen beenden sollte – wobei dies nur ein möglicher Abbruchindikator ist13.
5. Bestimmung der Abbruchkriterien
Bei der Auswahl eines Abbruchpunkts (sowohl bei den Rangierten Einkaufsentscheidungen als auch in der Realität) hängen die Kriterien von vielen Variablen ab. Beispielsweise könnte man über ein bescheidenes Budget verfügen, wodurch die Maximierung des ROI aufgrund besonders knapper Margen problematisch wird. Alternativ ist es möglich, dass man ein übergeordnetes Ziel bezüglich des Servicelevels hat und diese Priorität mit dem Streben nach Maximierung der Gewinnmargen in Einklang bringen muss.
Um noch detaillierter vorzugehen, könnten die Abbruchkriterien ein Streben nach maximiertem ROI mit variierenden Servicelevel-Zielen für jedes Produkt oder jede Kategorie umfassen. Die Abbruchkriterien sind daher eine strategische Entscheidung, die nach einer ehrlichen Reflexion über die übergeordneten Geschäftsziele eines Unternehmens getroffen werden sollte. Priorisierte Bestandsauffüllung (PIR) ist diesbezüglich bemerkenswert flexibel; die Abbruchkriterien für jeden Einkaufszyklus können unter Verwendung desselben Gesamtrangordnungsverfahrens angepasst werden.
Für anschauliche Visualisierungen unserer möglichen Bestandsauffüllungsentscheidungen gibt es für jedes Produkt drei Diagramme und Grafiken im Charts-Dashboard (Blatt 3, siehe Abbildung 14). Besonders interessant ist „Driving forces_product name“ (im Beispiel wird in Abbildung 14 Keyboard verwendet), das die Entwicklung des ROI bei unterschiedlichen Bestellmengen auf Einheitenebene zeigt.
Wie im Diagramm ersichtlich, gibt es einen Punkt, an dem steigende Bestellmengen zu einem negativen ROI führen. Dies liegt daran, dass es ab einem bestimmten Niveau keinen Sinn mehr macht, weitere Einheiten zu kaufen, da unsere erwarteten Margen durch höhere erwartete Lagerhaltungskosten kritisch reduziert werden.
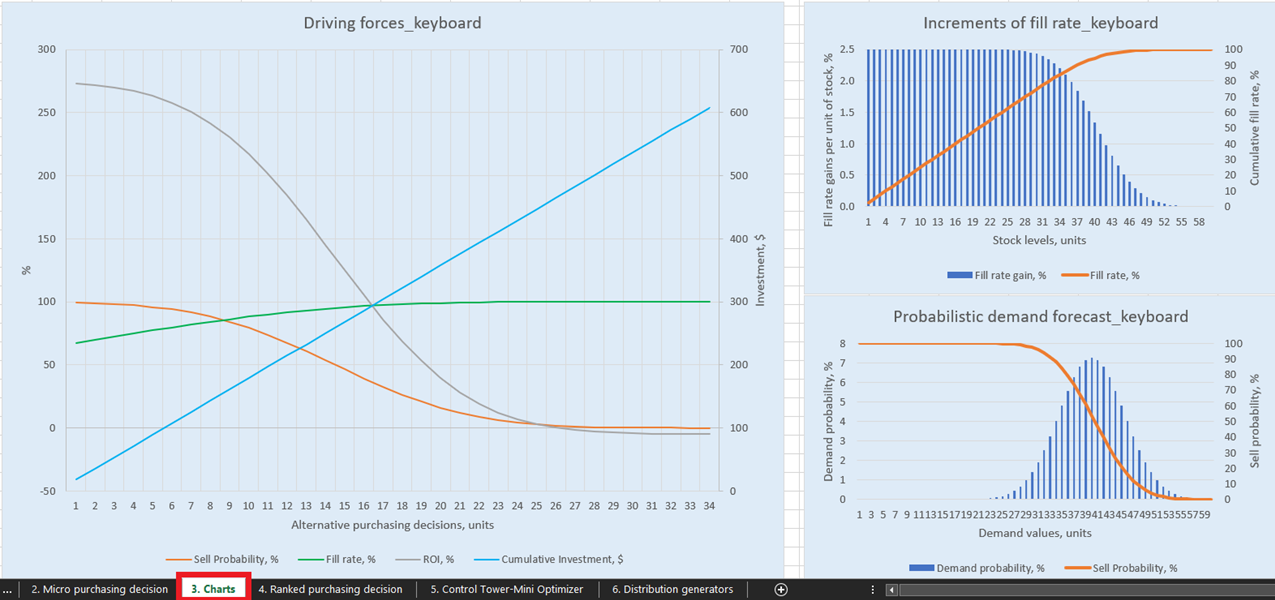
Abbildung 14. Ansicht von „Driving forces_keyboard“ im Bereich Charts, Ort in Rot hervorgehoben.
Sobald die Abbruchkriterien festgelegt sind, werden die priorisierten Bestandsauffüllungsentscheidungen pro SKU aggregiert, was wiederum die Menge, Investment und die erwartete Erfüllungsquote in der Output-Purchase Recommendation für jede SKU aktualisiert (siehe Abbildung 15). Man kann Budgetbeschränkungen (0 $ bis 1450 $) ändern, was wiederum die empfohlene Einkaufsliste aktualisiert. Der Einfachheit halber verfügt der Control Tower über zwei zusätzliche Bereiche: Base Case – hard copy und Changes to base scenario. Letzterer ist statisch und zeigt die Standardeinstellungen für die Demonstration, wie sie von Lokad entworfen wurden; der andere zeigt den Unterschied zwischen vorgenommenen Änderungen und Lokads Standardeinstellung.
Die Einkaufsempfehlungsliste im Control tower stellt das Ziel dieser Demonstration dar (siehe Abbildung 15).
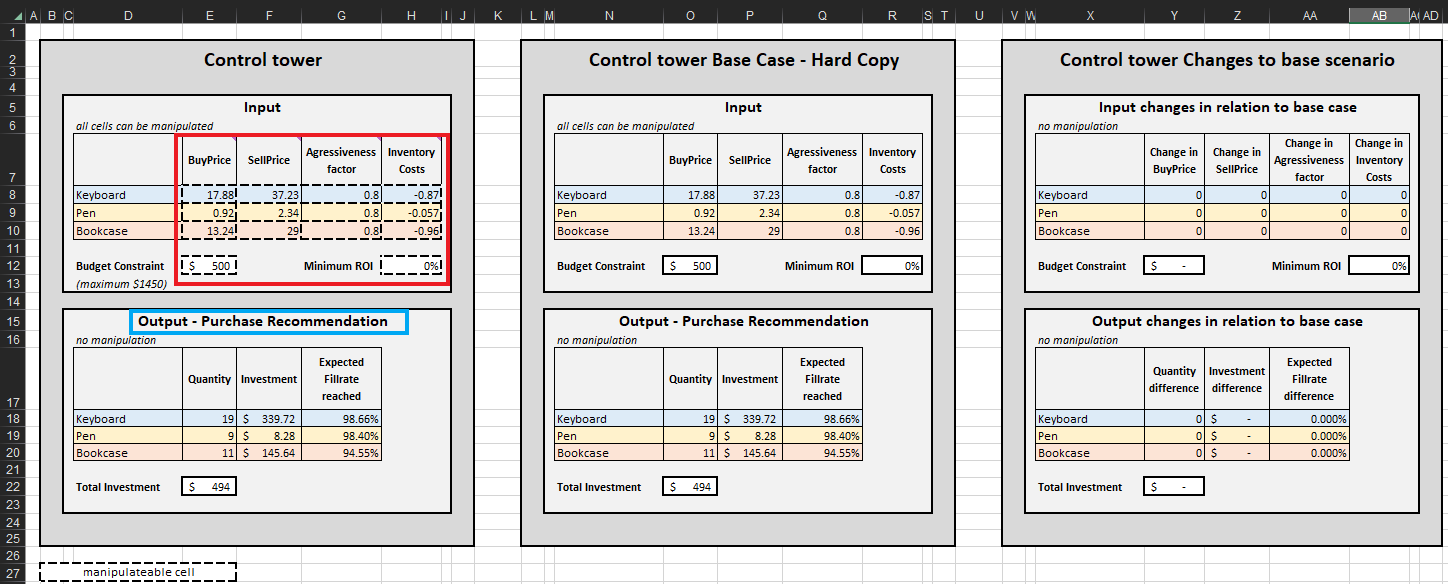
Abbildung 15. Ansicht des Control Tower-Mini Optimizer (Blatt 5). Die manipulierbaren Zellen sind in Rot hervorgehoben. „Purchase recommendation“ ist in Blau markiert und stellt das Ziel eines priorisierten Bestandsauffüllungsansatzes dar.
6. Fazit
Traditionelle Zeitreihenprognosen sind schlicht nicht in der Lage, das notwendige Granularitätsniveau zu erfassen, das erforderlich ist, um Bestandsauffüllungsentscheidungen zu treffen, die zukünftige Unsicherheiten sowie das volle Ausmaß der eigenen Einschränkungen und Treiber widerspiegeln. Dies liegt daran, dass ihnen eine explizite Unsicherheitsdimension fehlt, die durch Wahrscheinlichkeitswerte für erwartete zukünftige Ergebnisse dargestellt wird. Da eine traditionelle Zeitreihe de facto blind gegenüber dieser Art von Daten ist, kommt eine klassische Bewältigungsstrategie wie Sicherheitsbestand einem Rätselraten gleich – zu wenig, und man verliert profitable Verkäufe mit positivem erwarteten ROI; zu viel, und man reduziert seinen ROI, indem man Einheiten bevorratet, die (wie in der Tabelle gezeigt) einen negativen erwarteten ROI aufweisen.
Priorisierte Bestandsauffüllung unter Nutzung probabilistischer Prognosen ist unsere Lösung für dieses Problem. Ein solcher Ansatz berücksichtigt Bestandsauffüllungsoptionen in Kombination anstatt isoliert. Dadurch können der erwartete finanzielle Ertrag unserer Bestandsauffüllungsoptionen vollständig quantifiziert und offengelegt werden. Die Grundlage eines solchen Ansatzes bildet die Übernahme von Unsicherheit und die Nutzung probabilistischer Prognoseeingaben. Dadurch gewinnt man zudem einen besseren Einblick, welche Servicelevels (pro SKU) sinnvolle finanzielle Erträge erzielen, anstatt willkürliche Zielvorgaben zu setzen.
Der in diesem Dokument demonstrierte PIR-Ansatz wurde unter Verwendung synthetischer Daten und enger Parameter entwickelt. Diese Entscheidungen wurden getroffen, um ein gängiges Werkzeug (Excel) einem ungewöhnlichen Zweck (PIR) anzupassen. Unter anderen notwendigen Zugeständnissen wurden SKUs und Einheiten (jeweils auf 3 und 100) begrenzt, um die Verarbeitungszeit zu reduzieren, da die Daten eines gesamten Katalogs (ganz zu schweigen von den Daten mehrerer Geschäfte) zu arbeitsintensiv wären. Zudem wurden keine supply chain constraints hinzugefügt. Entscheidend ist, dass Excel nicht dafür ausgelegt ist, Zufallsvariablen zu verarbeiten – ein wesentlicher Schritt bei der Erstellung probabilistischer Prognosen und der PIR-Politik. Diese Einschränkungen gelten nicht für eine produktionstaugliche PIR-Lösung.
Supply chain practitioners, deren Unternehmen Excel überholt haben, sind eingeladen, eine E-Mail an contact@lokad.com zu senden, um eine Demonstration einer produktionstauglichen PIR-Lösung zu vereinbaren.
7. Überblick über die Tabelle
7.1 Lies mich
Dieses Blatt dient als Startseite für den Benutzer. Es gibt einen Link zu einem Online-Tutorial (dem, das Sie gerade lesen).
7.2 Mikro-Beschaffungsentscheidungen
Dies ist das zweite Blatt und widmet sich der fein granulären finanziellen Analyse aller möglichen Optionen für Bestandsauffüllungsentscheidungen. Bitte beachten Sie, dass hier keine manuelle Datenmanipulation erfolgt. Dieses Blatt zeigt lediglich die Ergebnisse von Berechnungen, die auf den Eingaben der Blätter Control Tower und Distribution generators basieren.
Hauptmerkmale:
- Zeilen mit bedingter Formatierung stellen „vergangene Entscheidungen“ dar und können nicht verändert werden. Wir empfehlen die Verwendung einer Desktop-Anwendung, da die browserbasierte Version von Excel hinsichtlich der Formatierung manchmal unzuverlässig ist.
- Wenn man über jeden Spaltenkopf fährt, wird eine hilfreiche Definition/Notiz angezeigt.
7.3 Diagramme
Dies ist das dritte Blatt und dient der Visualisierung der Haupttreiber, die bei den Entscheidungen zur Bestandsauffüllung eine Rolle spielen. Bitte beachten Sie, dass hier keine manuelle Datenmanipulation erfolgt. Dieses Blatt wurde entwickelt, um dem Anwender zu helfen, die Funktionsweise des PIR-Prozesses zu visualisieren (und dadurch besser zu verstehen).
Hauptmerkmale:
- Drei Diagramme pro SKU (Tastatur, Stift und Bücherregal).
- Das Diagramm „driving forces“ visualisiert die wichtigsten Triebkräfte für jede Entscheidung auf Einheitenebene (für jede SKU). Deshalb enthält die x-Achse nur Einheiten einer SKU, die noch nicht bestellt wurden.
- Zwei weitere Diagramme („increments of fill rate“ und „probabilistic demand forecast“) umfassen alle Lagereinheiten – sowohl den vorhandenen Bestand als auch die bestellbaren Einheiten.
7.4 Rangierte Einkaufsentscheidungen
Dies ist das vierte Blatt und dient der Auflistung aller möglichen Bestandsauffüllungsentscheidungen, sortiert nach ROI/Score in absteigender Reihenfolge. Diese Liste wird automatisch aus den Daten des Blatts 2 (Mikro-Beschaffungsentscheidungen) erstellt. Mögliche Entscheidungen werden zueinander ins Verhältnis gesetzt (siehe „Hauptmerkmale“ unten). Bitte beachten Sie, dass hier keine manuelle Datenmanipulation erfolgt. Abhängig von den in den Blättern 5 und 6 vorgenommenen Änderungen der Eingaben wird sich diese Liste verändern.
Hauptmerkmale:
- Mögliche Bestandsauffüllungsentscheidungen werden in absteigender Reihenfolge (von höchstem zu niedrigstem) nach ROI/Score gerankt.
- Die kumulative Investition wird für die sortierten Entscheidungen berechnet (siehe Spalte AA in Blatt 4).
- Wenn man über jeden Spaltenkopf fährt, wird eine hilfreiche Definition/Notiz angezeigt.
7.5 Control Tower-mini Optimierer
Dies ist das fünfte Blatt und fasst die Modellannahmen (Eingaben) sowie die empfohlenen Entscheidungen (Ausgaben) zusammen. Daten in veränderbaren Zellen können angepasst werden, um die Modellannahmen und damit das Modellergebnis zu ändern.
Hauptmerkmale:
- Drei Blöcke zur Unterstützung der Demonstration: „Control tower“ für die manuelle Manipulation der Eingaben; „Base Case – Hard copy“ zur Anzeige der Standardeinstellungen; und „Changes to base scenario“ zur Darstellung der Unterschiede zwischen den aktualisierten und den Standardeinstellungen (siehe Blatt 5).
- Ein vierter Block („Model Assumptions“), der unter „Control tower“ angeordnet ist, widmet sich der Anpassung der anfänglichen Lagerbestandsannahmen (siehe Blatt 5).
- Nur Daten in veränderbaren Zellen können geändert werden.
7.6 Distributionsgeneratoren
Dies ist das sechste Blatt und widmet sich der Erstellung probabilistischer Nachfrageprognosen. Parameter in veränderbaren Zellen können geändert werden, wodurch sich die Verteilungen aktualisieren und neue Wahrscheinlichkeits-Nachfragewerte angezeigt werden.
Hauptmerkmale:
- Ein Verteilungsdiagramm pro SKU.
- Jede SKU weist ein anderes Verteilungsmuster auf (die Begründung wird in Abschnitt 2.1 erläutert).
- Links von der Reihe der Verteilungsdiagramme befindet sich eine Tabelle, die der Anpassung der Parameter der Verteilungen gewidmet ist.
- Nur Parameter in veränderbaren Zellen können geändert werden.
- Wenn man über die relevanten Spaltenköpfe (in der Tabelle) fährt, wird eine hilfreiche Definition/Notiz angezeigt.
Anmerkungen
-
Drei Produkte genügen, um das Konzept zu veranschaulichen und das Dokument zugleich prägnant und übersichtlich zu halten. ↩︎
-
Lagerbestände werden probabilistisch, wenn wir probabilistische Nachfrage von diskreten Lagerwerten subtrahieren (diskreter Wert minus Wahrscheinlichkeitsverteilung ergibt eine weitere Wahrscheinlichkeitsverteilung). All dies würde es zu kompliziert machen, die Zusammenhänge in Excel zu erklären, da es nicht dafür ausgelegt ist, Berechnungen mit Zufallsvariablen durchzuführen (denken Sie an ‚Nachfragewahrscheinlichkeitsverteilungen‘). ↩︎
-
Diese Zugeständnisse sind notwendig, um das Grundprinzip eines probabilistischen Ansatzes zu demonstrieren. In der Realität werden rückständige Aufträge nicht immer genutzt und Lieferzeiten sind probabilistisch und Änderungen unterworfen. ↩︎
-
Der Einfachheit halber haben wir keine supply chain constraints angewendet. ↩︎
-
Wie bereits erwähnt, müssen in Mikro-Beschaffungsentscheidungen keine Daten bearbeitet werden. Sämtliche Datenmanipulationen erfolgen über die Blätter 5 und 6. ↩︎
-
In diesem Excel-Blatt werden wirtschaftliche Antriebe in Dollar ausgedrückt, obwohl die Währung im Grunde irrelevant ist. ↩︎
-
Die Liste wirtschaftlicher Treiber oben ist nicht umfassend, und reale Bestandsauffüllungs- (und supply chain-) Szenarien werden nahezu mit Sicherheit noch mehr enthalten. Dies gilt insbesondere beim Umgang mit der Produktion von Waren und Verderblichkeitsbeschränkungen. ↩︎
-
Dieser Treiber ist im B2C-Kontext vager als im B2B-Bereich. Im letzteren Fall gibt es oft explizite Strafzahlungen im Zusammenhang mit Ausverkaufsereignissen, wie vertragliche Strafzahlungen; im ersteren Fall ist es schwierig, den negativen finanziellen Einfluss eines Ausverkaufsereignisses zu quantifizieren. Im Allgemeinen ist er hoch bei Produkten, die einen überproportional negativen Einfluss auf die Attraktivität eines Unternehmens haben (unabhängig vom direkten Margenbeitrag der SKU). Milch, wie bereits erwähnt, ist kein Margentreiber für Supermärkte, aber ihre strategische Platzierung (in der Regel im hinteren Bereich des Supermarkts) veranlasst Kunden dazu, Gang für Gang an anderen Produkten vorbeizugehen (von denen fast alle höhere Margen aufweisen). Erlebt ein Supermarkt ein Ausverkaufsereignis mit diesem Grundnahrungsmittel (das Produkt, das die Leute sehr regelmäßig und in Körben kaufen), könnte dies dazu führen, dass Kunden den Supermarkt verlassen, woanders einkaufen und möglicherweise nicht zurückkehren (falls diese Ausverkaufsereignisse regelmäßig auftreten). ↩︎
-
Die Verkaufswahrscheinlichkeit wird aus den in Distribution generators (Blatt 6) erstellten Wahrscheinlichkeitsverteilungen abgeleitet. ↩︎
-
Die laufenden Kosten dafür, dass eine SKU nicht verkauft wird und somit eine nicht verkaufte Einheit gelagert werden muss. ↩︎
-
In diesem Szenario entspricht die Investition dem Einkaufspreis, allerdings nur, weil unsere Kaufentscheidungen nicht durch Mindestbestellmengen (MOQs) oder Losgrößenmultiplikatoren eingeschränkt sind. ↩︎
-
Der einfachste Weg, dies zu bewerkstelligen, besteht darin, den Aggressivitätsfaktor (Spalte S in Abbildung 12) auf Null zu setzen – etwas, das ein Unternehmen tun könnte, wenn es davon ausgeht, dass ein Ausverkaufsereignis keine negativen Auswirkungen hat. Ein kleiner, aber kostenloser Rat: Das tut es definitiv. ↩︎
-
Zum Beispiel beträgt unser Standardbudget 500 $, sodass wir unsere Kaufentscheidungen bei Zelle 40 (siehe Abbildung 13) beenden würden, da Zelle 41 einen Wert von 506,88 $ aufweist und damit über unserem Budget liegt. Anschließend würden wir die Zahlen pro Produkt aggregieren, was unsere Einkaufsliste darstellt (siehe Output – Purchase recommendation im Control Tower, gemäß Abbildung 2). Wie bereits erwähnt, kann das voreingestellte Budget von 500 $ (siehe Abbildung 2 für Anweisungen) auf einen beliebigen Wert zwischen 0 $ und 1450 $ angepasst werden. Dies zeigt, wie sich die Einkaufsliste bei unterschiedlichen Budgetbeschränkungen verändert. Unabhängig von finanziellen Einschränkungen werden ranked purchase decisions aus ROI-Perspektive die bestmögliche Kombination von Bestandsentscheidungen für alle Zeilen zwischen Rang 1 und dem Endpunkt identifizieren. ↩︎