Fonction de perte Pinball

learn menu
Par Joannès Vermorel, février 2012

La fonction de perte Pinball, également appelée perte de quantile, est une métrique utilisée pour évaluer l’exactitude d’une prévision de quantile.

Évaluer l’exactitude d’une prévision de quantile est un problème subtil. En effet, contrairement aux prévisions classiques où l’objectif est d’avoir la prévision aussi proche que possible des valeurs observées, la situation est biaisée (volontairement) en ce qui concerne les prévisions de quantile. Ainsi, la comparaison naïve observé vs prévisions n’est pas satisfaisante. La fonction de perte Pinball renvoie une valeur qui peut être interprétée comme l’exactitude d’un modèle de prévision de quantile.

Formule

Soit $${\tau}$$ le quantile cible, $${y}$$ la valeur réelle et $${z}$$ la prévision de quantile, alors $${L_\tau}$$, la fonction de perte Pinball, peut être écrite :

$${ \begin{eqnarray} L_{\tau}(y,z) & = & (y - z) \tau & \textrm{ si } y \geq z \\\ & = & (z - y) (1 - \tau) & \textrm{ si } z > y \end{eqnarray} }$$

Télécharger : pinball-loss-function.xlsx

La feuille de calcul illustre comment calculer la fonction de perte Pinball dans Microsoft Excel. La formule réelle n’est pas plus compliquée que la plupart des indicateurs d’exactitude tels que le MAPE.

Illustration

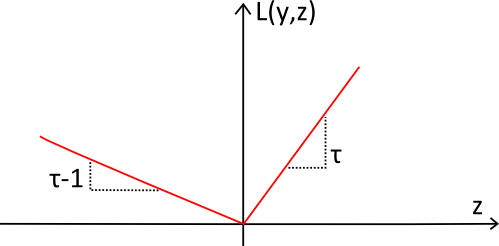
/pinball-loss-function

La fonction de perte Pinball (en rouge) a été nommée ainsi en raison de sa forme qui ressemble à la trajectoire d’une balle sur un flipper. La fonction est toujours positive et plus on s’éloigne de la cible $${y}$$, plus la valeur de $${L_\tau(y,z)}$$ est grande. La pente est utilisée pour refléter le déséquilibre souhaité dans la prévision de quantile.

Le meilleur modèle de quantile a la plus faible perte Pinball

Le résultat le plus important associé à la fonction de perte Pinball est que plus la perte Pinball est faible, plus la prévision de quantile est précise.

On peut prouver que la fonction qui minimise la perte Pinball fournit également le quantile optimal. Cependant, le formalisme requis pour la preuve dépasse le cadre de cet article.

Ainsi, pour comparer l’exactitude respective de deux modèles de quantile (par exemple Lokad vs autre), il suffit de calculer la perte Pinball moyenne de chaque modèle sur un nombre de séries temporelles suffisamment grand pour s’assurer que la différence observée est statistiquement significative. En pratique, quelques centaines de séries temporelles suffisent pour évaluer quel modèle de quantile est le plus précis.

Le piège de Lokad

La simplicité supposée de la notion d’exactitude pour une prévision classique (c’est-à-dire une prévision moyenne) est selon nous largement surestimée. Les prévisions, qu’il s’agisse de la moyenne ou du quantile, sont sujettes au surapprentissage, ce qui complique considérablement la comparaison des modèles de prévision. Cependant, la fonction de perte Pinball constitue un moyen très simple d’évaluer l’exactitude relative de deux modèles de prévision de quantile.

Pour en savoir plus