Prévision probabiliste (Supply Chain)

Une prévision est dite probabiliste, plutôt que déterministe, si elle contient un ensemble de probabilités associées à toutes les issues futures possibles, au lieu de désigner une issue particulière comme “la” prévision. Les prévisions probabilistes sont importantes chaque fois que l’incertitude est irréductible, ce qui est presque toujours le cas lorsqu’il s’agit de systèmes complexes. Pour les supply chains, les prévisions probabilistes sont essentielles pour produire des décisions robustes face à des conditions futures incertaines. En particulier, la demande et le délai d’approvisionnement, deux aspects clés de l’analyse de la supply chain, sont tous deux mieux abordés via la prévision probabiliste. La perspective probabiliste se prête naturellement à la hiérarchisation économique des décisions en fonction de leurs rendements attendus mais incertains. Une grande variété de modèles statistiques fournit des prévisions probabilistes. Certains sont structurellement proches de leurs homologues déterministes, tandis que d’autres sont très différents. L’évaluation de la précision d’une prévision probabiliste nécessite des mesures spécifiques, qui diffèrent de celles utilisées pour les prévisions déterministes. L’exploitation des prévisions probabilistes requiert des outils spécialisés qui diffèrent de leurs homologues déterministes.

Prévisions déterministes vs. probabilistes

L’optimisation des supply chains repose sur la bonne anticipation des événements futurs. Numériquement, ces événements sont anticipés par des prévisions, qui englobent une grande variété de méthodes numériques utilisées pour quantifier ces événements futurs. Depuis les années 1970, la forme de prévision la plus utilisée a été la prévision déterministe des séries temporelles: une quantité mesurée au fil du temps – par exemple, la demande en unités pour un produit – est projetée dans le futur. La partie passée de la série temporelle correspond aux données historiques, tandis que la partie future correspond à la prévision.

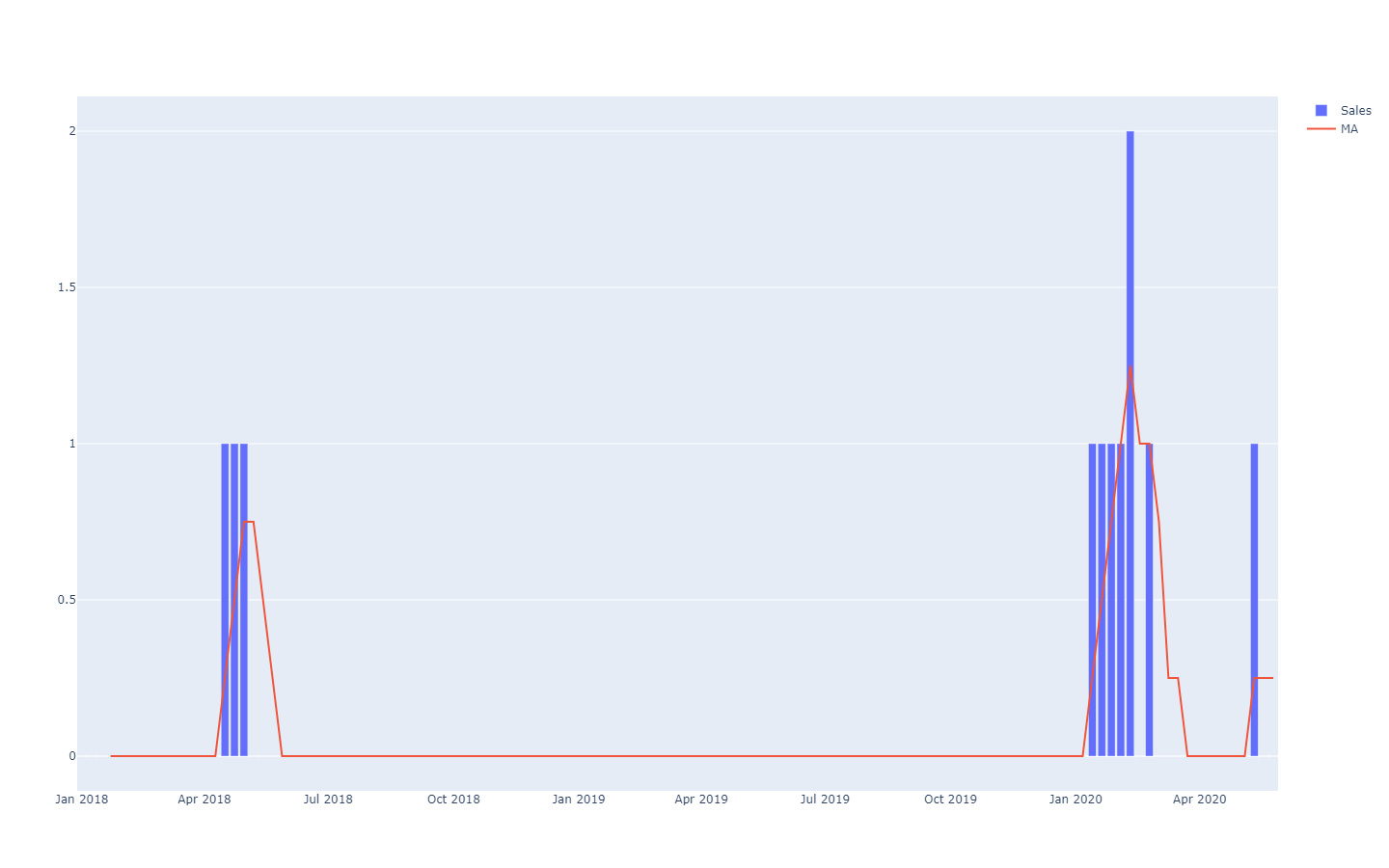
Ces prévisions de séries temporelles sont dites déterministes car, pour chaque instant futur, la prévision fournit une unique valeur censée correspondre le plus précisément possible au résultat futur. En effet, bien que la prévision soit unique, il est largement admis qu’elle a peu de chances d’être parfaitement correcte. Les résultats futurs divergeront de la prévision. L’adéquation de la prévision déterministe à ses résultats futurs est évaluée de manière quantitative à l’aide de métriques de précision, telles que l’erreur quadratique moyenne (MSE) par exemple.

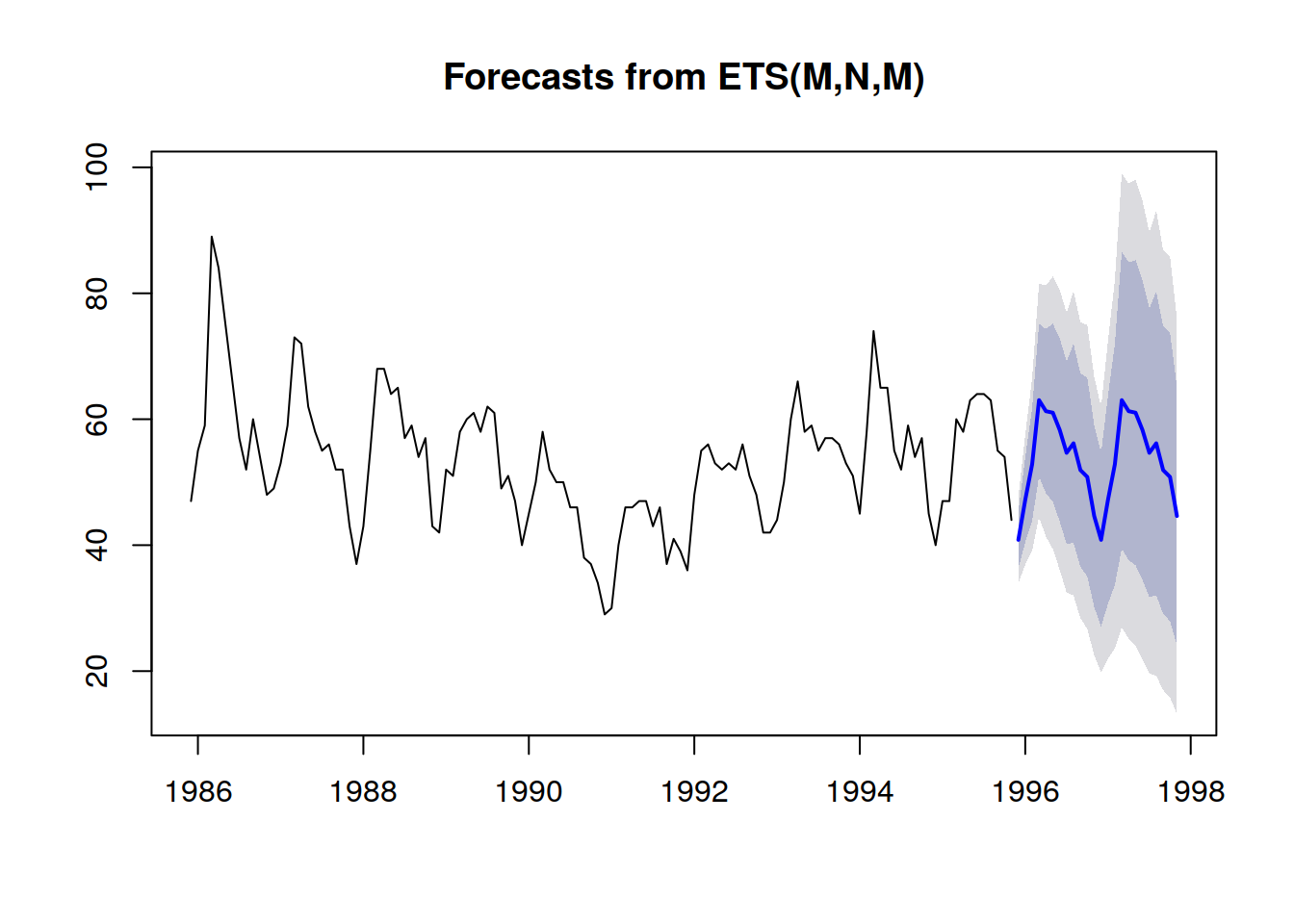
Les prévisions probabilistes adoptent une perspective différente dans l’anticipation des résultats futurs. Au lieu de produire une unique valeur comme résultat “optimal”, la prévision probabiliste consiste à attribuer une probabilité à chaque résultat possible. En d’autres termes, tous les événements futurs restent possibles, ils ne sont simplement pas également probables. Ci-dessous se trouve la visualisation d’une prévision de séries temporelles probabiliste illustrant l’“effet fusil”, que l’on observe typiquement dans la plupart des situations réelles. Nous reviendrons sur cette visualisation avec plus de détails dans la suite.

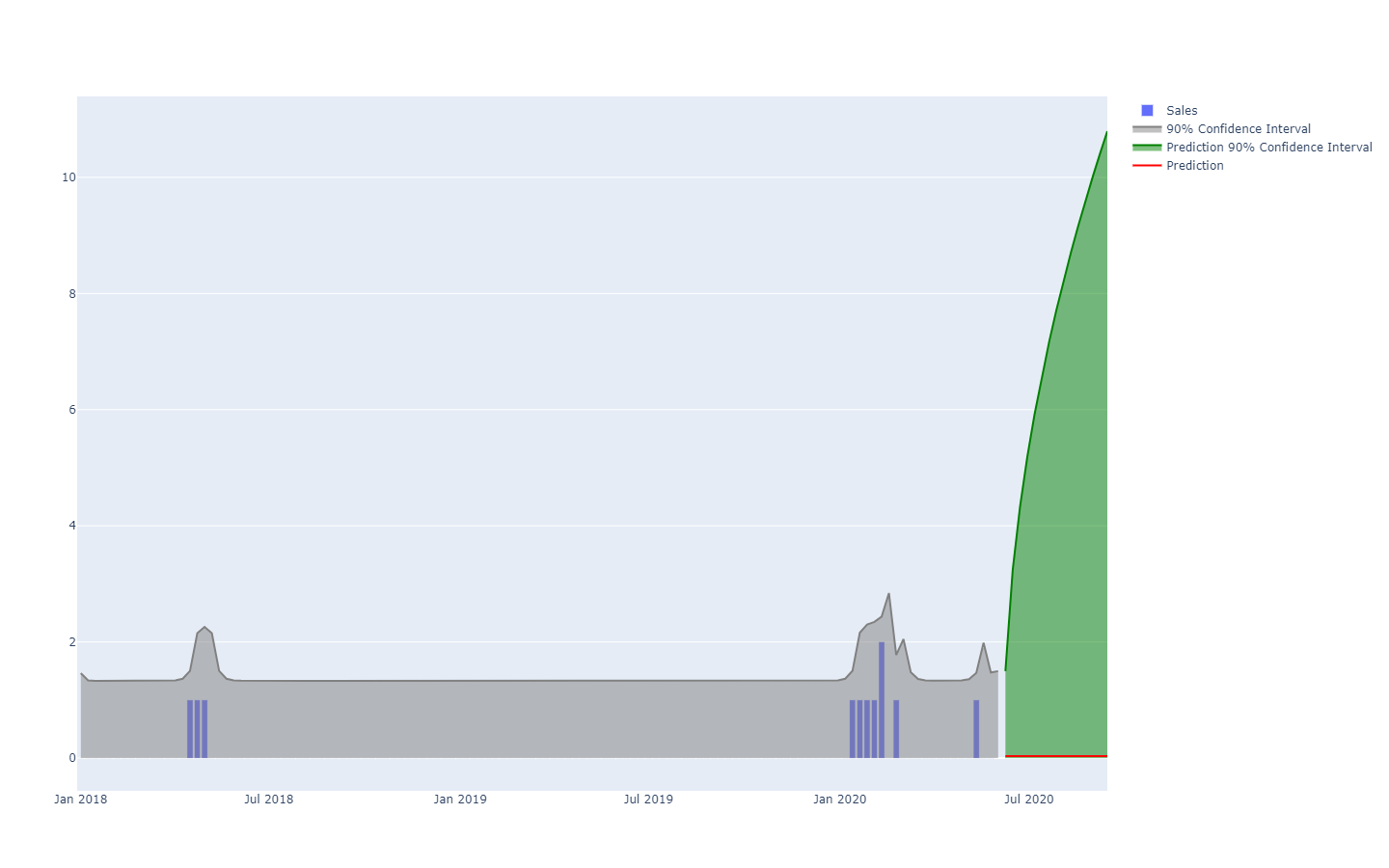
Les séries temporelles, c’est-à-dire une quantité mesurée au fil du temps, sont probablement le modèle de données le plus connu et le plus utilisé. Ce modèle de données peut être prédit à la fois par des moyens déterministes ou probabilistes. Cependant, il existe de nombreux modèles de données alternatifs, généralement plus riches, qui se prêtent également à des prévisions des deux types. Par exemple, une entreprise qui répare des moteurs d’avion pourrait souhaiter anticiper la liste exacte des pièces de rechange qui seront nécessaires pour une opération de maintenance à venir. Cette anticipation peut prendre la forme d’une prévision, mais ce ne sera pas une prévision de séries temporelles. La prévision déterministe associée à cette opération est la liste exacte des pièces et de leurs quantités. À l’inverse, la prévision probabiliste correspond à la probabilité pour chaque combinaison de pièces (quantités incluses) que cette combinaison spécifique sera celle nécessaire pour effectuer les réparations.

De plus, bien que le terme “prévision” souligne une forme d’anticipation, l’idée peut être généralisée à tout type d’énoncé statistiquement inféré à propos d’un système, y compris pour ses propriétés passées (mais inconnues). La pratique de la prévision statistique a émergé au cours du 20e siècle, avant l’avènement de la perspective plus moderne de l’apprentissage statistique, qui englobe toutes les extrapolations basées sur les données pouvant être effectuées, quelle que soit la dimension temporelle. Pour plus de clarté, nous continuerons à utiliser le terme “prévision” dans la suite, même si l’aspect temporel assimile toujours le passé à ce qui est connu et le futur à ce qui est inconnu. Par exemple, une entreprise peut souhaiter estimer les ventes qui auraient eu lieu pour un produit dans un magasin si le produit n’avait pas été en rupture de stock ce jour-là. Cette estimation est utile pour quantifier l’ampleur du problème en termes de qualité de service. Cependant, puisque l’événement appartient au passé, le chiffre de ventes “réel” ne sera jamais observé. Néanmoins, en supposant qu’il n’ait pas encore été trivialement observé, l’estimation statistique de la demande passée est un problème très proche de l’estimation de la demande future.

Les prévisions probabilistes sont plus riches – en termes d’information – que leurs homologues déterministes. Alors que la prévision déterministe fournit une “meilleure estimation” du résultat futur, elle ne dit rien des alternatives. En fait, il est toujours possible de convertir une prévision probabiliste en son équivalent déterministe en prenant la moyenne, la médiane, le mode, … de la distribution de probabilité. Cependant, l’inverse n’est pas vrai : il n’est pas possible de retrouver une prévision probabiliste à partir d’une prévision déterministe.

Pourtant, bien que les prévisions probabilistes soient statistiquement supérieures aux prévisions déterministes, elles restent peu utilisées dans la supply chain. Cependant, leur popularité a progressivement augmenté au cours de la dernière décennie. Historiquement, les prévisions probabilistes sont apparues plus tard, car elles nécessitent des ressources informatiques significativement plus importantes. Exploiter les prévisions probabilistes à des fins de supply chain requiert également des outils logiciels spécialisés, qui sont souvent indisponibles.

Cas d’utilisation de la supply chain

L’optimisation d’une supply chain consiste à prendre la décision “appropriée” – au moment présent – qui permettra de traiter de la manière la plus profitable une situation future qui n’est qu’imparfaitement estimée. Cependant, l’incertitude associée aux événements futurs est en grande partie irréductible. Ainsi, l’entreprise a besoin que la décision soit robuste même si l’anticipation de l’événement futur – c’est-à-dire la prévision – est imparfaite. Cela a été réalisé minimalement depuis le milieu du 20e siècle par l’analyse des stocks de sécurité. Cependant, comme nous le verrons ci-dessous, mis à part l’intérêt historique, il n’y a plus aucune raison de favoriser les stocks de sécurité par rapport aux recettes numériques “natives” probabilistes.

La perspective de la prévision probabiliste adopte une position radicale face à l’incertitude : cette approche tente de quantifier l’incertitude autant que possible. Dans la supply chain, les coûts tendent à se concentrer sur les extrêmes statistiques : c’est la demande exceptionnellement élevée qui crée la rupture de stock, et c’est la demande exceptionnellement faible qui provoque la dépréciation des stocks. Entre-temps, les stocks se renouvellent sans problème. Les prévisions probabilistes sont – pour le dire grossièrement – une tentative de gestion de ces situations à faible fréquence et à coût élevé qui sont omniprésentes dans les modern supply chains. Les prévisions probabilistes peuvent et doivent être considérées comme un ingrédient clé de toute pratique de gestion des risques au sein de la supply chain.

De nombreux aspects des supply chains sont particulièrement adaptés à la prévision probabiliste, tels que :

• demande : les vêtements, accessoires, pièces de rechange ; ainsi que de nombreux autres types de produits, tendent à être associés à une demande erratique et/ou intermittente. Les lancements de produits peuvent être des succès ou des échecs. Les promotions des concurrents peuvent temporairement et de manière erratique cannibaliser de grandes parts de marché.
• délai d’approvisionnement : les importations outre-mer peuvent subir toute une série de retards à n’importe quel stade de la chaîne (production, transport, douane, réception, etc.). Même les fournisseurs locaux peuvent, de façon occasionnelle, présenter de longs délais s’ils rencontrent un problème de rupture de stock. Les délais tendent à suivre des distributions à “queue lourde”.
• rendement (produits frais) : la quantité et la qualité de la production de nombreux produits frais dépendent de conditions, telles que la météo, qui sont hors du contrôle de l’entreprise. La prévision probabiliste quantifie ces facteurs pour toute la saison et offre la possibilité d’aller au-delà de l’horizon de pertinence des prévisions météo classiques.
• retours (le e-commerce) : lorsqu’un client commande le même produit en trois tailles différentes, il y a de fortes chances que deux de ces tailles soient retournées. Plus généralement, bien que d’importantes différences régionales existent, les clients tendent à profiter des politiques de retour favorables lorsqu’elles existent. La probabilité de retours pour chaque commande doit être évaluée.
• rebuts (aviation) : les pièces d’avion réparables – souvent appelées rotables – ne parviennent parfois pas à être réparées. Dans ce cas, la pièce est mise au rebut, car elle ne peut jamais être remontée sur un avion. Bien qu’il soit généralement impossible de savoir à l’avance si une pièce survivra à sa réparation ou non, il convient d’estimer les chances que cette pièce soit mise au rebut.
• stocks (B2C retail) : les clients peuvent déplacer, endommager ou même voler des marchandises dans un magasin de détail. Ainsi, le niveau de stocks électronique n’est qu’une approximation de la disponibilité réelle en rayon telle que perçue par les clients. Le niveau de stocks, tel que perçu par les clients, devrait être estimé à l’aide d’une prévision probabiliste.
• …

Cette courte liste illustre que les angles propices à une prévision probabiliste dépassent de loin le seul angle traditionnel de la “prévision de la demande”. L’optimisation bien conçue d’une supply chain nécessite de prendre en compte toutes les sources d’incertitude pertinentes. Bien qu’il soit parfois possible de réduire l’incertitude – comme le souligne la lean manufacturing – il y a généralement des compromis économiques en jeu, et, par conséquent, une certaine part d’incertitude reste irréductible.

Les prévisions, cependant, ne sont que des opinions éclairées sur l’avenir. Bien que les prévisions probabilistes puissent être considérées comme des opinions remarquablement détaillées, elles ne diffèrent pas fondamentalement de leurs homologues déterministes à cet égard. La valeur, du point de vue de la supply chain, des prévisions probabilistes réside dans la manière dont cette structure fine est exploitée pour produire des décisions plus rentables. En particulier, on ne s’attend généralement pas à ce que les prévisions probabilistes soient plus précises que leurs homologues déterministes si l’on utilise des métriques de précision déterministes pour évaluer la qualité des prévisions.

En défense de la variabilité

Contrairement à ce que préconisent de nombreuses approches de la supply chain, la variabilité est là pour rester – d’où la nécessité des prévisions probabilistes. La première idée reçue est que la variabilité est nécessairement néfaste pour une supply chain ; ce n’est pas le cas. La deuxième idée reçue est que la variabilité peut être éliminée par conception ; ce n’est pas possible.

La variabilité a des implications positives pour les supply chains dans de multiples situations. Par exemple, du côté de la demande, la plupart des secteurs sont portés par la nouveauté, comme la mode, les produits culturels, le luxe accessible et le luxe haut de gamme – tout comme les entreprises aux résultats “incertains”. La plupart des nouveaux produits ne rencontrent pas le succès (ce sont des échecs), mais ceux qui réussissent (les succès) génèrent des retours massifs. Une variabilité accrue est bénéfique car elle augmente la probabilité de retours hors norme, tandis que les inconvénients restent plafonnés (dans le pire des cas, l’ensemble des stocks est radié). Le flux ininterrompu de nouveaux produits mis sur le marché garantit le renouvellement constant des “succès”, tandis que les anciens s’estompent.

Du côté de l’offre, un processus de sourcing qui garantit des offres de tarification très variables est supérieur – toutes choses égales par ailleurs – à un processus alternatif qui génère des prix beaucoup plus cohérents (c’est-à-dire moins variables). En effet, l’option la moins chère est sélectionnée tandis que les autres sont écartées. Il n’importe peu que le prix “moyen” obtenu soit faible, l’essentiel étant de découvrir des sources à prix encore plus bas. Ainsi, un bon processus de sourcing devrait être conçu pour accroître la variabilité, par exemple en mettant l’accent sur l’exploration régulière de nouveaux fournisseurs plutôt que de restreindre le processus de sourcing aux fournisseurs bien établis.

Parfois, la variabilité peut être bénéfique pour des raisons plus subtiles. Par exemple, si une marque est trop prévisible en ce qui concerne ses opérations promotionnelles, les clients en identifient le schéma et commencent à retarder leur achat, sachant qu’une promotion est à venir et quand elle interviendra. La variabilité – voire l’irrégularité – des activités promotionnelles atténue ce comportement dans une certaine mesure.

Un autre exemple est la présence de facteurs de confusion au sein même de la supply chain. Si les nouveaux produits sont toujours lancés avec à la fois une campagne télévisée et une campagne radio, il devient statistiquement difficile de distinguer les impacts respectifs du télé et de la radio. Ajouter de la variabilité à l’intensité des campagnes en fonction de chaque canal permet d’extraire par la suite davantage d’informations statistiques issues de ces opérations, qui peuvent ensuite être transformées en insights pour une meilleure répartition des ressources marketing.

Naturellement, toute variabilité n’est pas bonne. La lean manufacturing a raison de souligner que, du côté de la production de la supply chain, la variabilité est habituellement préjudiciable, surtout lorsqu’il s’agit de délais variables. En effet, des processus LIFO (dernier entré, premier sorti) peuvent accidentellement apparaître, ce qui, à son tour, exacerbe la variabilité des délais de livraison. Dans ces situations, la variabilité accidentelle doit être éliminée, généralement grâce à un meilleur processus, parfois par de meilleurs équipements ou installations.

La variabilité - même lorsqu’elle est préjudiciable - est fréquemment irréductible. Comme nous le verrons dans la section suivante, les supply chains obéissent à la loi des petits nombres. Il est illusoire de penser que le niveau au magasin pourra un jour être prédit de manière fiable - d’un point de vue déterministe - alors que les clients ne savent pas toujours eux-mêmes ce qu’ils vont acheter. Plus généralement, réduire la variabilité entraîne toujours un coût (et la réduire davantage coûte encore plus cher), tandis que la réduction marginale de la variabilité n’apporte que des rendements décroissants. Ainsi, même lorsque la variabilité peut être réduite, pour ainsi dire, elle peut très rarement être complètement éliminée en raison des implications économiques.

La Loi des Petits Nombres

La loi des petits nombres de la supply chain peut être énoncée ainsi : les petits nombres prévalent partout le long de la chaîne. Cette loi empirique résulte des économies d’échelle et de quelques autres forces qui gouvernent la plupart des aspects structurels des supply chains:

• un fournisseur qui fournit des dizaines de milliers d’unités de matériaux par jour est susceptible d’avoir des quantités minimales de commande (MOQ) ou des paliers de prix qui empêchent que les commandes d’achat soient passées trop fréquemment. Le nombre de commandes d’achat passées à un fournisseur un jour donné dépasse rarement un chiffre.
• une usine qui produit des dizaines de milliers d’unités par jour est susceptible d’opérer par grandes séries de milliers d’unités. La production est généralement emballée par palettes entières. Le nombre de séries pendant une journée donnée est au plus un petit nombre à deux chiffres.
• un entrepôt qui reçoit des dizaines de milliers d’unités par jour est susceptible d’être approvisionné par des camions, chaque camion déchargeant l’intégralité de sa cargaison dans l’entrepôt. Le nombre de livraisons de camions un jour donné dépasse rarement un nombre à deux chiffres, même pour les très grands entrepôts.
• un magasin de détail pouvant contenir des dizaines de milliers d’unités en stocks est susceptible d’étaler son assortiment sur des milliers de références produits distinctes. Le nombre d’unités en stocks pour chaque produit dépasse très rarement un chiffre.
• …

Naturellement, en modifiant l’unité de mesure, il est toujours possible d’exagérer les chiffres. Par exemple, si au lieu de compter le nombre de palettes nous comptons le nombre de grammes de palettes, ou leur valeur monétaire en cents USD, de grands nombres apparaissent. Cependant, la loi des petits nombres doit être comprise avec la notion de compter les choses d’un point de vue sensé de la supply chain. Alors qu’en théorie ce principe peut paraître assez subjectif, ce n’est pas le cas en pratique, en raison des contraintes discrètes évidentes des supply chains modernes : bundles, boîtes, palettes, conteneurs, camions …

Cette loi revêt une grande importance pour la perspective de la prévision probabiliste. Tout d’abord, elle montre que les prévisions discrètes dominent dans les situations de supply chain, c’est-à-dire que le résultat à anticiper (ou à décider) est un entier, par opposition à un nombre fractionnaire. Les prévisions probabilistes sont particulièrement adaptées aux situations discrètes, car une probabilité peut être estimée pour chaque résultat discret. En revanche, les prévisions déterministes peinent avec les issues discrètes. Par exemple, que signifie-t-il que les ventes quotidiennes attendues d’un produit soient de 1,3 unité ? Les unités ne se vendent pas fractionnellement. Bien que des interprétations « discrètes » plus sensées puissent être déduites de cette déclaration, sa contrepartie probabiliste (par exemple, 27 % de chance d’une demande de 0 unité, 35 % de chance d’une demande de 1 unité, 23 % de chance d’une demande de 2 unités, etc.) est bien plus directe, car elle prend en compte la nature discrète du phénomène étudié.

Deuxièmement, bien que les prévisions probabilistes puissent sembler radicalement plus exigeantes en termes de ressources informatiques, ce n’est pas vraiment le cas en pratique, précisément en raison de la loi des petits nombres. En effet, pour revenir aux ventes quotidiennes de produits évoquées ci-dessus, il ne sert à rien d’évaluer numériquement les chances que la demande dépasse 100 un jour donné. Ces probabilités peuvent être arrondies à zéro - ou à une valeur arbitrairement faible. L’impact sur la précision numérique du modèle de supply chain reste négligeable. En règle générale, il est raisonnable de considérer que les prévisions probabilistes nécessitent environ trois ordres de grandeur de ressources informatiques en plus que leurs homologues déterministes. Cependant, malgré ce surcoût, les bénéfices en termes de performance de la supply chain dépassent de loin le coût des ressources informatiques.

Métriques de précision pour les prévisions probabilistes

Quoi qu’il arrive, une prévision probabiliste raisonnablement conçue indique qu’il existait en effet une probabilité non nulle que ce résultat se produise. Cela est intrigant car, à première vue, il pourrait sembler que les prévisions probabilistes étaient en quelque sorte immunisées contre la réalité, à l’image d’un diseur de bonne aventure formulant des prédictions extrêmement ambiguës qui ne peuvent jamais être infirmées, puisque ce dernier peut toujours fournir une explication rétrospective sur la manière d’interpréter correctement ces prédictions. En réalité, il existe plusieurs manières d’évaluer quantitativement la qualité d’une prévision probabiliste. Certaines de ces approches constituent des métriques semblables en esprit aux métriques utilisées pour évaluer la précision des prévisions déterministes, tandis que d’autres s’écartent de façon plus radicale et plus profonde par rapport à la perspective déterministe.

Examinons brièvement quatre approches distinctes pour évaluer la précision d’une prévision probabiliste :

• la fonction de perte pinball
• le score de probabilité classée continu (CRPS)
• la vraisemblance bayésienne
• la perspective générative antagoniste

La fonction de perte pinball fournit une métrique de précision permettant d’obtenir une estimation de quantile à partir d’une prévision probabiliste. Par exemple, si nous souhaitons évaluer la quantité de stock qui a 98 % de chance d’être supérieure ou égale à la demande client dans un magasin pour un produit donné, cette quantité peut être obtenue directement à partir des prévisions probabilistes en additionnant simplement les probabilités à partir de 0 unité de demande, 1 unité de demande, … jusqu’à ce que la probabilité dépasse 98 %. La fonction de perte pinball fournit une mesure directe de la qualité de cette estimation biaisée de la demande future. Elle peut être considérée comme un outil pour évaluer la qualité de n’importe quel point de la fonction de densité cumulée de la prévision probabiliste.

Le score de probabilité classée continu (CRPS) fournit une métrique qui peut être interprétée comme la « quantité de déplacement » de la masse de probabilités nécessaire pour déplacer toute la masse de probabilité vers le résultat observé. C’est la généralisation la plus directe de l’erreur absolue moyenne (MAE) dans une perspective probabiliste. La valeur du CRPS est homogène avec l’unité de mesure du résultat lui-même. Cette perspective peut être généralisée à des espaces métriques arbitraires, au lieu de se limiter à des situations unidimensionnelles, grâce à ce que l’on appelle la « théorie du transport » et la distance de Monge-Kantorovich (qui dépasse le cadre du présent document).

La vraisemblance et sa cousine d’entropie croisée adoptent la perspective bayésienne du moindre degré de surprise : plus la probabilité des résultats observés est élevée, mieux c’est. Par exemple, nous avons deux modèles probabilistes A et B : le modèle A indique que la probabilité d’observer 0 unité de demande est de 50 % pour un jour donné, tandis que le modèle B indique qu’elle est de 1 % pour un jour donné. Nous observons la demande pendant 3 jours et obtenons les observations suivantes : 0, 0, 1. Le modèle A avait environ 10 % de chances de générer ces observations, tandis que pour le modèle B, cela se situait autour de 0,01 %. Ainsi, le modèle B est bien moins susceptible d’être le modèle correct comparé au modèle A. La vraisemblance s’écarte de la perspective déterministe, qui cherche à disposer d’un critère absolu significatif pour évaluer les modèles. Au contraire, elle fournit un mécanisme pour comparer les modèles, mais numériquement, ce mécanisme ne peut servir qu’à cette comparaison.

La perspective générative antagoniste est la plus moderne en la matière (Ian Goodfellow et al., 2014). Essentiellement, cette perspective affirme que le « meilleur » modèle probabiliste est celui qui peut être utilisé pour générer des résultats - à la manière de Monte Carlo - qui sont indistinguables des résultats réels. Par exemple, si nous envisageons la liste historique des transactions dans un hypermarché local, nous pourrions tronquer cette histoire à un moment arbitraire dans le passé et utiliser le modèle probabiliste pour générer par la suite des transactions factices mais réalistes. Le modèle serait considéré comme « parfait » s’il était impossible, au moyen d’une analyse statistique, de retrouver le moment où l’ensemble de données passe de données « réelles » à des données « factices ». Le but de l’approche générative antagoniste est d’« apprendre » les métriques qui mettent en évidence le défaut de tout modèle probabiliste. Plutôt que de se focaliser sur une métrique particulière, cette approche exploite de façon récursive les techniques de machine learning pour « apprendre » les métriques elles-mêmes.

La recherche de meilleures méthodes pour évaluer la qualité des prévisions probabilistes reste un domaine actif. Il n’existe pas de démarcation nette entre les questions « Comment produire une meilleure prévision ? » et « Comment savoir si une prévision est meilleure ? ». Des travaux récents ont considérablement brouillé les frontières entre les deux, et il est probable que les prochaines avancées impliqueront des changements supplémentaires dans la manière même d’envisager les prévisions probabilistes.

Probabilités infinitésimales et log likelihood

De très petites probabilités apparaissent naturellement lorsqu’on examine une situation multidimensionnelle à travers le prisme des prévisions probabilistes. Ces faibles probabilités posent problème parce que les ordinateurs ne traitent pas des nombres d’une précision infinie. Les valeurs brutes de probabilité sont fréquemment « infinitésimales » dans le sens où elles sont arrondies à zéro en raison des limites de la précision numérique. La solution à ce problème n’est pas de mettre à niveau le logiciel pour des calculs en précision arbitraire - ce qui serait très inefficace en termes de ressources informatiques - mais d’utiliser le « log-trick », qui transforme les multiplications en additions. Ce procédé est utilisé - d’une manière ou d’une autre - par pratiquement chaque logiciel traitant des prévisions probabilistes.

Supposons que nous ayons $$X_1, X_2, \ldots, X_n$$ des variables aléatoires représentant la demande du jour pour chacun des $$n$$ produits distincts desservis dans un magasin donné. Soient $$\hat{x}_1, \hat{x}_2, \ldots, \hat{x}_n$$ la demande empirique observée à la fin de la journée pour chaque produit. Pour le premier produit - régi par $$X_1$$ - la probabilité d’observer $$\hat{x}_1$$ s’écrit $$P(X_1=\hat{x}_1)$$. Maintenant, supposons, de manière quelque peu abusive mais pour les besoins de la clarté, que tous les produits soient strictement indépendants en termes de demande. La probabilité de l’événement conjoint d’observer $$\hat{x}_1, \hat{x}_2, \ldots, \hat{x}_n$$ est :

Si $$P(X_k=\hat{x}_k) \approx \tfrac{1}{2}$$ (approximation grossière) et $$n=10000$$, alors la probabilité conjointe ci-dessus est de l’ordre de $$\tfrac{1}{{2^{10000}}} \approx 5 \times 10^{-3011}$$, ce qui est une valeur très faible. Cette valeur entraîne un underflow, c’est-à-dire qu’elle tombe en dessous du plus petit nombre représentable, même en considérant les nombres à virgule flottante 64 bits généralement utilisés pour le calcul scientifique.

Le « log-trick » consiste à travailler avec le logarithme de l’expression, c’est-à-dire :

Le logarithme transforme la série de multiplications en une série d’additions, ce qui s’avère beaucoup plus stable numériquement qu’une série de multiplications.

L’utilisation du « log-trick » est fréquente dès qu’il s’agit de prévisions probabilistes. Le log likelihood est, à proprement parler, le logarithme de la vraisemblance (introduite précédemment) précisément parce que la vraisemblance brute serait généralement numériquement non représentable compte tenu des types courants de nombres à virgule flottante.

Variantes algorithmiques des prévisions probabilistes

La question de la génération informatisée de prévisions probabilistes est presque aussi vaste que le domaine du machine learning lui-même. Les délimitations entre ces deux champs, s’il en existe, relèvent principalement du choix subjectif. Néanmoins, cette section présente une liste plutôt sélective d’approches algorithmiques notables pouvant être utilisées pour obtenir des prévisions probabilistes.

Au début du 20e siècle, possiblement à la fin du 19e siècle, l’idée du stock de sécurité est apparue, où l’incertitude de la demande est modélisée selon une distribution normale. Comme des tables pré-calculées de la distribution normale avaient déjà été établies pour d’autres sciences, notamment la physique, l’application du stock de sécurité ne nécessitait qu’une multiplication d’un niveau de demande par un coefficient de « stock de sécurité » extrait d’une table préexistante. Anecdotiquement, de nombreux manuels de supply chain rédigés jusqu’aux années 1990 contenaient encore des tables de la distribution normale dans leurs annexes. Malheureusement, le principal inconvénient de cette approche est que les distributions normales ne constituent pas une proposition raisonnable pour les supply chains. Premièrement, en ce qui concerne les supply chains, il est raisonnable de supposer que rien n’est jamais distribué normalement. Deuxièmement, la distribution normale est une distribution continue, ce qui est en contradiction avec la nature discrète des événements de la supply chain (voir « Loi des Petits Nombres » ci-dessus). Ainsi, bien que techniquement les « safety stocks » comportent une composante probabiliste, la méthodologie sous-jacente et les recettes numériques sont résolument orientées vers la perspective déterministe. Cette approche est néanmoins mentionnée ici pour plus de clarté.

Fast forward to the early 2000s, ensemble learning methods - whose most well-known representatives are probably random forests and gradient boosted trees - are relatively straightforward to extend from their deterministic origins to the probabilistic perspective. The key idea behind ensemble learning is to combine numerous, weak, deterministic predictors, such as decision trees, into a superior deterministic predictor. However, it is possible to adjust the mixing process to obtain probabilities rather than just a single aggregate, hence turning the ensemble learning method into a probabilistic forecasting method. These methods are non-parametric and capable of fitting fat-tailed and/or multimodal distributions, as commonly found in the supply chain. These methods tend to have two notable downsides. First, by construction, the density probability function produced by this class of models tends to include a lot of zeroes, which prevents any attempts at leveraging the log-likelihood metric. More generally, these models don’t really fit the Bayesian perspective, as newer observations are frequently declared “impossible” (i.e. zero probability) by the model. This problem however can be solved through regularization methods¹. Second, models tend to be as large as a sizable fraction of the input dataset, and the “predict” operation tends to be almost as computationally costly as the “learn” operation.

Les méthodes hyper-paramétriques regroupées sous le nom de « deep learning », qui ont émergé de manière explosive dans les années 2010, étaient, presque accidentellement, probabilistes. En effet, alors que la grande majorité des tâches où deep learning excelle vraiment (par exemple, la classification d’images) se concentrent uniquement sur des prévisions déterministes, il s’avère que la métrique de l’entropie croisée - une variante du log-vraisemblance discuté ci-dessus - présente des gradients très raides qui conviennent fréquemment à la descente de gradient stochastique (SGD), qui est au cœur des méthodes de deep learning. Ainsi, les modèles de deep learning se révèlent être conçus comme probabilistes, non pas parce que les probabilités intéressaient, mais parce que la descente de gradient converge plus rapidement lorsque la fonction de perte reflète une prévision probabiliste. Ainsi, en ce qui concerne le deep learning, la supply chain se distingue par son intérêt pour la sortie probabiliste réelle du modèle de deep learning, tandis que la plupart des autres cas d’utilisation réduisent la distribution de probabilité à sa moyenne, médiane ou mode. Les Mixture Density Networks sont un type de réseau de deep learning destiné à apprendre des distributions de probabilité complexes. Le résultat lui-même est une distribution paramétrique, éventuellement composée de Gaussiennes. Cependant, contrairement aux « stocks de sécurité », un mélange de plusieurs Gaussiennes peut, en pratique, refléter les comportements à queue épaisse qui sont observés dans les supply chains. Bien que les méthodes de deep learning soient fréquemment considérées comme étant à la pointe de la technologie, il faut noter que parvenir à une stabilité numérique, surtout lorsque des mélanges de densités sont impliqués, reste un peu un « art obscur ».

La programmation différentiable est un descendant du deep learning, qui a gagné en popularité à la toute fin des années 2010. Elle partage de nombreuses caractéristiques techniques avec le deep learning, mais diffère significativement en termes d’approche. Alors que le deep learning se concentre sur l’apprentissage de fonctions arbitrairement complexes (c’est-à-dire jouer au Go) en empilant un grand nombre de fonctions simples (c’est-à-dire des couches convolutionnelles), la programmation différentiable se focalise sur la structure fine du processus d’apprentissage. La structure la plus granulaire et la plus expressive, littéralement, peut être formatée comme un programme, qui implique des branches, des boucles, des appels de fonction, etc. La programmation différentiable est d’un grand intérêt pour la supply chain, car les problèmes ont tendance à se présenter de manière très structurée, et ces structures sont connues des experts². Par exemple, les ventes d’une certaine chemise peuvent être cannibalisées par une autre chemise d’une couleur différente, mais ne le seront pas par les ventes d’une chemise de trois tailles de différence. De tels a priori structurels sont essentiels pour atteindre une grande efficacité en matière de données. En effet, du point de vue de la supply chain, la quantité de données tend à être très limitée (cf. la loi des petits nombres). D’où, encadrer structurellement le problème aide à garantir que les schémas statistiques désirés soient appris, même en cas de données limitées. Les a priori structurels aident également à résoudre les problèmes de stabilité numérique. Comparé aux méthodes d’apprentissage par ensemble, les a priori structurels tendent à être une affaire moins chronophage que l’ingénierie des caractéristiques ; la maintenance du modèle est également simplifiée. En revanche, la programmation différentiable reste une perspective relativement naissante à ce jour.

La perspective de Monte Carlo (1930 / 1940) peut être utilisée pour aborder les prévisions probabilistes sous un angle différent. Les modèles évoqués jusqu’à présent fournissent des fonctions de densité de probabilité (PDF) explicites. Cependant, dans une perspective de Monte Carlo, un modèle peut être remplacé par un générateur - ou échantillonneur - qui génère aléatoirement des résultats possibles (parfois appelés « déviates »). Les PDF peuvent être récupérées en moyennant les résultats du générateur, bien que les PDF soient fréquemment contournées afin de réduire les exigences en termes de ressources informatiques. En effet, le générateur est souvent conçu pour être infiniment plus compact - en termes de données - que les PDF qu’il représente. La plupart des méthodes de machine learning - y compris celles mentionnées ci-dessus pour aborder directement les prévisions probabilistes - peuvent contribuer à l’apprentissage d’un générateur. Les générateurs peuvent prendre la forme de modèles paramétriques de faible dimension (par exemple, les modèles à espace d’états) ou de modèles hyper-paramétriques (par exemple, les modèles LSTM et GRU en deep learning). Les méthodes d’apprentissage par ensemble sont rarement utilisées pour soutenir les processus génératifs en raison de leurs coûts de calcul élevés pour leurs opérations de « prédiction », qui sont largement exploitées pour soutenir l’approche de Monte Carlo.

Working with probabilistic forecasts

Extraire des informations utiles et prendre des décisions à partir de prévisions probabilistes nécessite des outils numériques spécialisés. Contrairement aux prévisions déterministes où les résultats sont de simples nombres, les prévisions elles-mêmes sont soit des fonctions de densité de probabilité explicites, soit des générateurs Monte Carlo. La qualité des outils probabilistes est, en pratique, aussi importante que la qualité des prévisions probabilistes. Sans ces outils, l’exploitation des prévisions probabilistes se transforme en un processus déterministe (plus d’informations dans la section « Antipatterns » ci-dessous).

Par exemple, les outils devraient être capables d’effectuer des tâches telles que :

• Combiner le délai de production incertain avec le délai de transport incertain, pour obtenir le délai incertain « total ».
• Combiner la demande incertaine avec le délai incertain, pour obtenir la demande incertaine « totale » devant être couverte par les stocks sur le point d’être commandés.
• Combiner les retours de commande incertains (le e-commerce) avec la date d’arrivée incertaine de la commande fournisseur en transit, pour obtenir le délai client incertain.
• Augmenter la prévision de la demande, produite par une méthode statistique, avec un risque de queue dérivé manuellement d’une compréhension globale d’un contexte non reflété par les données historiques, tel qu’une pandémie.
• Combiner la demande incertaine avec un état incertain des stocks en ce qui concerne la date d’expiration (distribution alimentaire), pour obtenir le stock résiduel incertain de fin de journée.
• …

Une fois que toutes les prévisions probabilistes - et pas seulement celles de la demande - sont correctement combinées, l’optimisation des décisions de supply chain devrait avoir lieu. Cela implique une perspective probabiliste sur les contraintes, ainsi que sur la fonction de score. Cependant, cet aspect des outils dépasse le cadre du présent document.

Il existe deux grandes « saveurs » d’outils pour travailler avec des prévisions probabilistes : d’abord, les algèbres sur variables aléatoires, ensuite, la programmation probabiliste. Ces deux approches se complètent car elles n’ont pas le même mélange d’avantages et d’inconvénients.

Une algèbre de variables aléatoires travaille généralement sur des fonctions de densité de probabilité explicites. L’algèbre supporte les opérations arithmétiques habituelles (addition, soustraction, multiplication, etc.) mais transposées à leurs homologues probabilistes, traitant fréquemment les variables aléatoires comme statistiquement indépendantes. L’algèbre offre une stabilité numérique presque équivalente à celle de son homologue déterministe (c’est-à-dire de simples nombres). Tous les résultats intermédiaires peuvent être conservés pour une utilisation ultérieure, ce qui s’avère très pratique pour organiser et déboguer le data pipeline. En revanche, l’expressivité de ces algèbres tend à être limitée, car il est généralement impossible d’exprimer toutes les subtiles dépendances conditionnelles qui existent entre les variables aléatoires.

La programmation probabiliste adopte une perspective de Monte Carlo pour aborder le problème. La logique est écrite une fois, généralement en adoptant une perspective entièrement déterministe, mais exécutée de nombreuses fois via les outils (c’est-à-dire le processus de Monte Carlo) afin de collecter les statistiques souhaitées. L’expressivité maximale est obtenue grâce à des constructions « programmatiques » : il est possible de modéliser des dépendances arbitraires et complexes entre les variables aléatoires. Rédiger la logique elle-même via la programmation probabiliste tend également à être légèrement plus facile comparé à une algèbre de variables aléatoires, puisque la logique n’implique que des nombres simples. En revanche, il existe un compromis constant entre la stabilité numérique (plus d’itérations offrent une meilleure précision) et les ressources informatiques (plus d’itérations coûtent plus cher). De plus, les résultats intermédiaires ne sont généralement pas facilement accessibles, car leur existence est seulement transitoire - précisément pour alléger la pression sur les ressources informatiques.

Des travaux récents en deep learning indiquent également que d’autres approches existent au-delà des deux présentées ci-dessus. Par exemple, les auto-encodeurs variationnels offrent des perspectives pour effectuer des opérations sur des espaces latents donnant des résultats impressionnants tout en recherchant des transformations très complexes sur les données (ex : supprimer automatiquement les lunettes d’un portrait photo). Bien que ces approches soient conceptuellement très intrigantes, elles n’ont pas démontré - à ce jour - une grande pertinence pratique lorsqu’il s’agit de résoudre des problèmes de supply chain.

Visualization of probabilistic forecasts

La manière la plus simple de visualiser une distribution de probabilité discrète est un histogramme, où l’axe vertical indique la probabilité et l’axe horizontal la valeur de la variable aléatoire d’intérêt. Par exemple, une prévision probabiliste d’un délai peut être affichée comme suit :

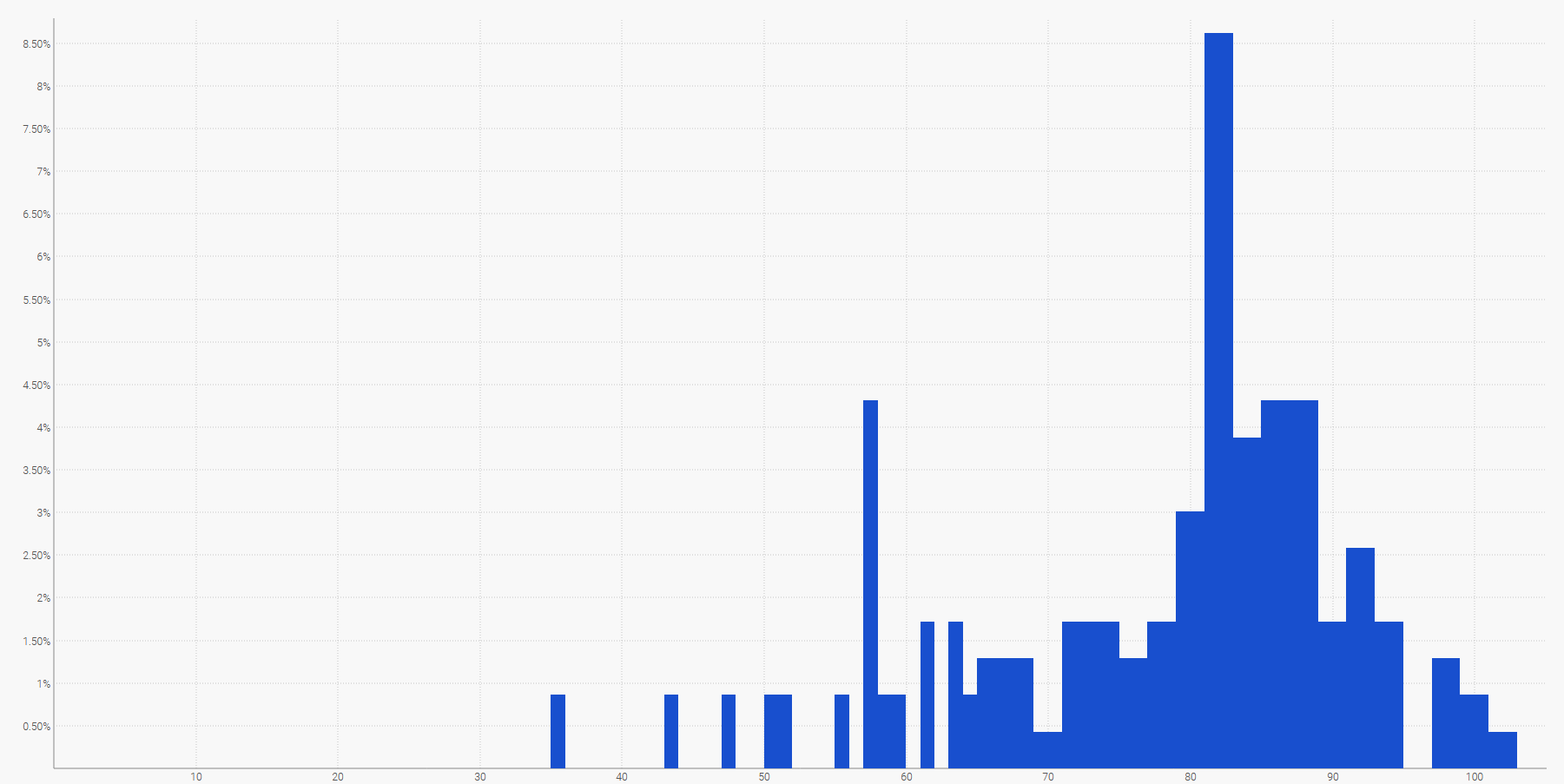
La demande future, cumulée sur une période de temps spécifiée, peut également être représentée par un histogramme. Plus généralement, l’histogramme est bien adapté à toutes les variables aléatoires unidimensionnelles sur $${ℤ}$$, l’ensemble des entiers relatifs.

La visualisation de l’équivalent probabiliste d’une série temporelle à intervalles réguliers - c’est-à-dire une quantité variant sur des périodes de temps discrètes de durée égale - est déjà beaucoup plus difficile. En effet, contrairement à la variable aléatoire unidimensionnelle, il n’existe pas de visualisation canonique d’une telle distribution. Attention, les périodes ne peuvent pas être considérées comme indépendantes. Ainsi, bien qu’il soit possible de représenter une série temporelle « probabiliste » en alignant une série d’histogrammes - un par période -, cette représentation déformerait gravement la manière dont les événements se déroulent dans une supply chain.

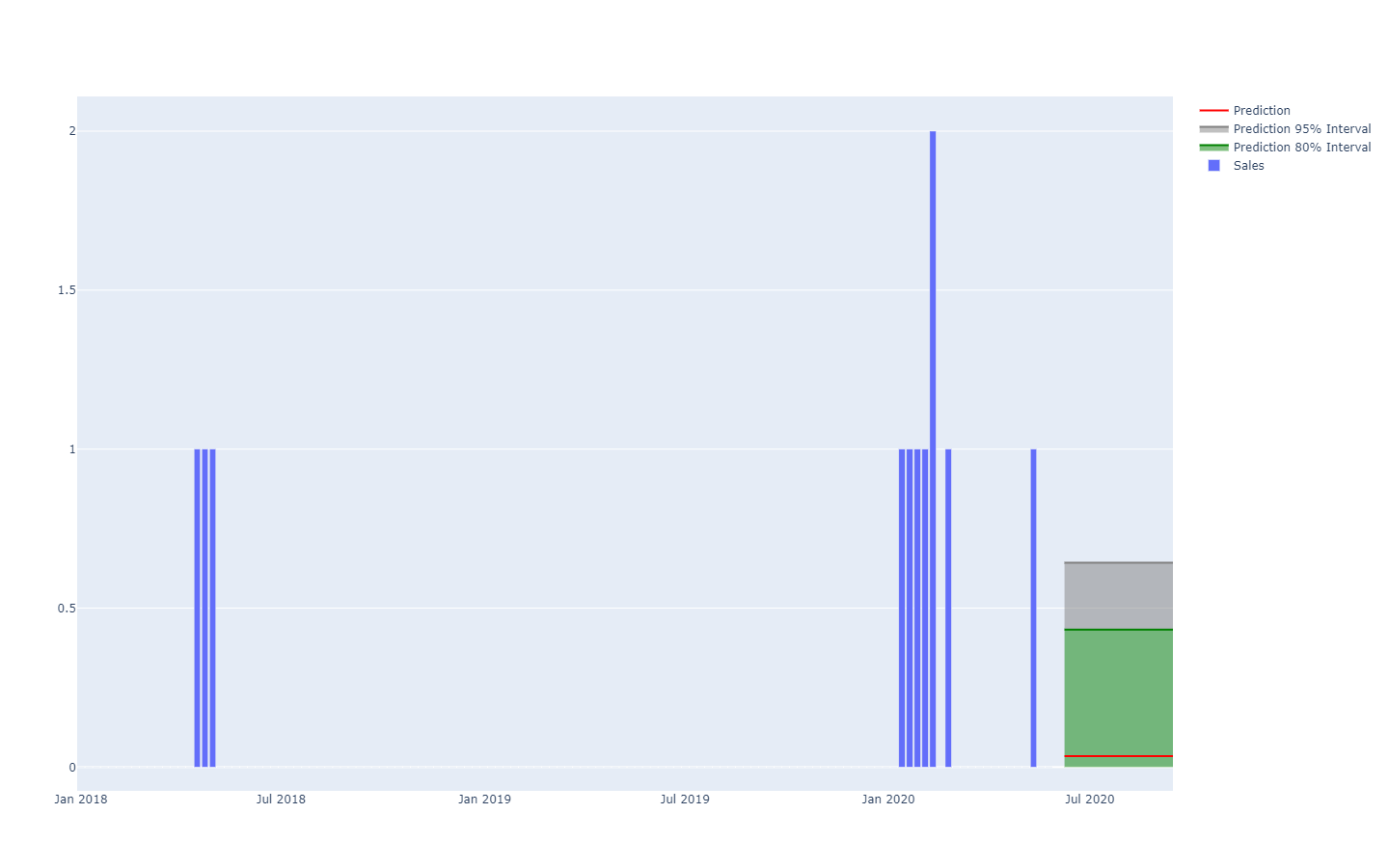
Par exemple, il n’est pas trop improbable qu’un produit nouvellement lancé performe bien et atteigne des volumes de vente élevés (un succès). Il n’est pas trop improbable non plus que le même produit nouvellement lancé échoue et génère de faibles volumes de vente (un échec). Cependant, d’immenses oscillations quotidiennes entre niveaux de vente de succès ou d’échec sont extrêmement improbables.

Les intervalles de prévision, comme on les trouve couramment dans la littérature sur la supply chain, peuvent être quelque peu trompeurs. Ils tendent à accentuer des situations de faible incertitude qui ne sont pas représentatives des situations réelles de supply chain;

Remarquez comment ces intervalles de prévision sont exactement les distributions de probabilité, disposées côte à côte avec un schéma de couleurs pour délimiter des seuils quantiles spécifiques.

Une meilleure représentation - c’est-à-dire qui ne supposent pas des dépendances inter-périodes fortes - consiste à examiner les valeurs cumulatives dans le temps, en prenant leurs quantiles, puis en différenciant pour obtenir des incréments par période (voir la première illustration d’une prévision probabiliste donnée au début du présent article). La visualisation est la même, mais le sens sous-jacent diffère. Nous examinons maintenant des quantiles sur des scénarios, délimitant les scénarios extrêmement favorables (resp. défavorables).

Probabilistic forecasting antipatterns

Les prévisions probabilistes remettent en question la manière dont beaucoup de gens pensent « intuitivement » à l’avenir. Dans cette section, nous abordons certains des aspects les plus fréquemment mal compris de la prévision probabiliste.

No such thing as ‘unpredictable’ events

Du point de vue déterministe, prédire le résultat de la loterie est impossible, car les chances de réussir sont « une sur un million ». Cependant, d’un point de vue probabiliste, le problème est trivial : chaque billet a une chance sur un million de gagner. La très haute variance du résultat ne doit pas être confondue avec une « inaccessibilité » du phénomène lui-même, qui peut être parfaitement compris, comme c’est le cas pour une loterie. La prévision probabiliste consiste à quantifier et structurer la variance, et non à l’éliminer.

No such thing as ‘normal’ distributions

Les distributions normales, également connues sous le nom de Gaussiennes, sont omniprésentes dans les manuels de supply chain et de physique. Pourtant, en ce qui concerne les affaires humaines, presque rien n’est distribué de manière “normale”. Les distributions normales, par conception, rendent les grandes déviations (comparées aux déviations moyennes) extrêmement rares, au point d’être considérées comme purement impossibles par le modèle - c’est-à-dire des probabilités inférieures à une sur un milliard. La demande, les délais de livraison, les retours sont autant de cas qui, catégoriquement, ne suivent pas une distribution normale. Le seul avantage des distributions normales est qu’elles se prêtent bien à la création d’exercices de manuels pour les étudiants, car elles admettent des solutions analytiques explicites.

Choix sélectif des probabilités

Lorsqu’on est confronté à une distribution de probabilités, il est tentant de choisir un point de la distribution, possiblement la moyenne ou la médiane, et de se baser sur ce chiffre. Ce procédé va à l’encontre de l’essence même de l’aspect probabiliste de la prévision. Les probabilités ne devraient pas être condensées en une simple estimation ponctuelle, car quel que soit le point choisi, ce procédé entraîne une perte massive d’information. Ainsi, aussi dérangeant que cela puisse paraître, les probabilités doivent être conservées telles quelles aussi longtemps que possible. Le point de convergence se trouve typiquement lors de la décision finale supply chain, qui maximise les rendements tout en faisant face à des incertitudes futures.

Éliminer les valeurs aberrantes statistiques

La plupart des méthodes numériques classiques - solidement ancrées dans la perspective déterministe des prévisions (ex. moyennes mobiles) - se comportent très mal lorsqu’elles rencontrent des valeurs aberrantes statistiques. Ainsi, de nombreuses entreprises mettent en place des processus pour “nettoyer” manuellement les données historiques de ces valeurs aberrantes. Cependant, ce besoin d’un tel processus de nettoyage ne fait qu’illustrer les limites de ces méthodes numériques. Au contraire, les valeurs aberrantes statistiques constituent un ingrédient essentiel de la prévision probabiliste, car elles permettent d’obtenir une meilleure vision de ce qui se passe à la queue de la distribution. En d’autres termes, ces valeurs aberrantes sont la clé pour quantifier la probabilité de rencontrer d’autres valeurs aberrantes.

Apporter une épée à un combat de fusils

Des outils spécialisés sont nécessaires pour manipuler les distributions de probabilités. Produire la prévision probabiliste n’est qu’une étape parmi tant d’autres pour apporter une réelle valeur ajoutée à l’entreprise. De nombreux praticiens de la supply chain en viennent à écarter les prévisions probabilistes faute d’outils adéquats pour en exploiter les résultats. De nombreux vendeurs de logiciels d’entreprise ont rejoint le mouvement et prétendent désormais supporter la “prévision probabiliste” (ainsi que “AI” et la “blockchain”), sans jamais aller au-delà d’une simple implémentation cosmétique de quelques modèles probabilistes (cf. la section ci-dessus). Présenter un modèle de prévision probabiliste ne vaut presque rien sans un ensemble d’outils étendu pour exploiter ses résultats numériques.

Notes