La prévision des méthodes et formules dans Excel

Ce guide explique les méthodes de prévision élémentaires qui peuvent être facilement appliquées dans des feuilles de calcul Microsoft Excel. Ce guide s’adresse aux managers et cadres qui ont besoin d’anticiper la demande des clients. La théorie est illustrée avec Microsoft Excel. Des notes avancées sont disponibles pour un développeur de logiciel qui souhaiterait reproduire la théorie dans une application personnalisée.
Les avantages de la prévision
La prévision peut vous aider à prendre les bonnes décisions et à gagner/économiser de l’argent. Voici un exemple.
- Dimensionnez vos stocks de façon optimale
Le temps c’est de l’argent. L’espace c’est de l’argent. Ce que vous voulez faire, c’est utiliser tous les moyens à votre disposition pour réduire vos stocks – sans subir de ruptures de stock, bien sûr.
Comment ? Par la prévision !
Pour faciliter les choses : étiquettes, commentaires, noms de fichiers
Au fil du temps, à mesure que vos données s’accumulent, il est de plus en plus probable que vous vous retrouviez confus et que vous commettiez des erreurs. La solution ? Ne soyez pas désordonné : utiliser judicieusement les étiquettes, les commentaires et nommer correctement vos fichiers peut vous éviter bien des soucis.
- Étiquetez toujours vos colonnes. Utilisez la première ligne de chaque colonne pour décrire les données qu’elle contient.
- Des données différentes, des colonnes différentes. Ne mettez pas des nombres différents (par exemple, vos coûts et vos ventes) dans la même colonne. Il est fort probable que vous vous y retrouviez confus, et cela complique les calculs ainsi que la gestion des données.
- Donnez à chaque fichier un nom clairement compréhensible. Cela demande peu d’effort et accélère les choses. Cela les rend faciles à identifier visuellement et plus simples à retrouver grâce à la fonction de recherche de Windows.
- Utilisez les commentaires.
Même si vous ne travaillez pas habituellement avec un grand volume de données, il est toujours très facile de se perdre. Cela est particulièrement vrai si vous revenez sur des données que vous avez créées il y a longtemps. Excel offre une excellente solution : les commentaires.

Il suffit de faire un clic droit sur la cellule que vous souhaitez commenter, puis de sélectionner « insérer un commentaire ».
Vous pouvez les utiliser :
- pour expliquer le contenu d’une cellule (c’est-à-dire le coût unitaire selon les estimations de M. Doe)
- pour laisser des avertissements aux futurs utilisateurs de la feuille (c’est-à-dire J’ai un doute sur ce calcul… )
Pour commencer : un exemple simple de prévision utilisant des courbes de tendance
Visualiser vos données
Réalisez maintenant votre première prévision. Dans cette partie, nous allons utiliser ce fichier : Example1.xls. Pour reproduire les étapes par vous-même, vous pouvez télécharger le fichier. Ces données ne servent qu’à titre d’exemple.
Nos données : Dans la première colonne, des données sur les coûts unitaires de produits similaires (le coût unitaire reflète la qualité du produit). Dans la deuxième, des données sur le volume vendu.
Ce que nous voulons savoir : Si nous vendons un autre produit, avec une qualité correspondant à un coût de 150 $/unité, combien d’unités pouvons-nous espérer vendre ?
Comment y parvenir : Ici, c’est assez simple. Nous voulons trouver une relation mathématique simple entre le coût unitaire et les ventes, puis utiliser cette relation pour effectuer notre prévision.
Tout d’abord, il est toujours utile de créer un graphique dans Excel, afin de jeter un coup d’œil aux données. Vos yeux sont d’excellents outils qui peuvent vous aider à identifier des tendances en quelques secondes.
Pour ce faire, nous sélectionnons nos données, puis utilisons Insertion > Graphique, et choisissons l’option XY (nuage de points). Nous souhaitons estimer les ventes en fonction de la qualité, donc nous plaçons le coût unitaire sur l’axe horizontal et les ventes sur l’axe vertical.
Maintenant, arrêtons-nous quelques secondes pour bien observer ce que nous voyons : la relation semble être croissante et linéaire.
Pour avoir une idée de la forme exacte de la relation, nous faisons un clic droit sur le graphique, puis sélectionnons l’option “Trendline”.
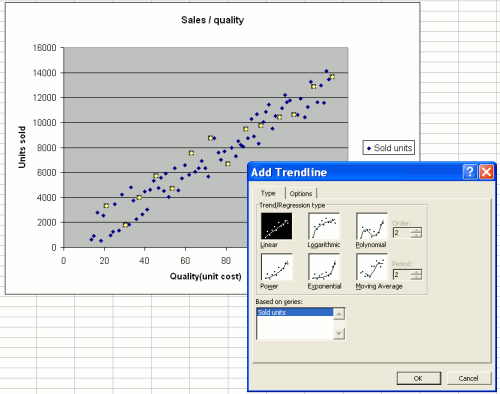
Maintenant, nous devons sélectionner la relation qui semble le mieux correspondre (c’est-à-dire décrire au mieux) à nos données. Encore une fois, nous utilisons notre regard : dans ce cas, les points sont presque alignés, donc nous utilisons le paramètre “linear”. Par la suite, nous utiliserons d’autres réglages - plus complexes, mais souvent plus réalistes - comme “exponential”.
Notre courbe de tendance est désormais affichée sur le graphique. Un autre clic droit nous permet d’afficher la forme exacte de la relation : y = 102.4x - 191.64.
Comprenez : Nombre d’unités vendues = 102.4 fois le coût unitaire - 191.64.
Ainsi, si nous décidons de produire à un coût unitaire de 150 $, nous pouvons nous attendre à vendre 102.4*150 - 191.64 = 15168 unités
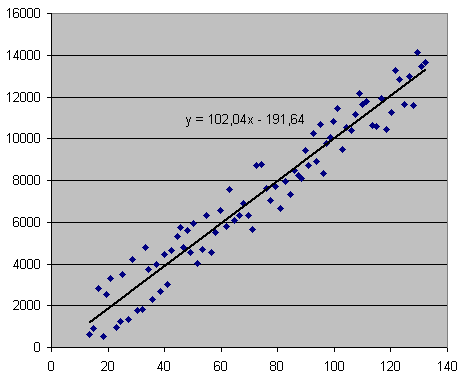
A linear trendline -> Une courbe de tendance linéaire
Nous venons de réaliser avec succès notre première prévision.
Cependant, attention : le logiciel est toujours capable de trouver une relation entre les deux colonnes, même si cette relation est en réalité très faible ! Par conséquent, une vérification de la robustesse est requise. Voici comment procéder rapidement :
- Tout d’abord, jetez toujours un coup d’œil au graphique. Si vous constatez que les points sont étroitement groupés autour de la courbe de tendance, comme dans notre exemple ci-dessus, il y a de fortes chances que la relation soit robuste. Cependant, si les points semblent être disposés de manière presque aléatoire et se trouvent généralement assez éloignés de la courbe de tendance, alors il faut être prudent : la corrélation est faible, et la relation estimée ne doit pas être prise pour acquise.
Les points sont partout : aucune relation évidente, prévisions peu fiables
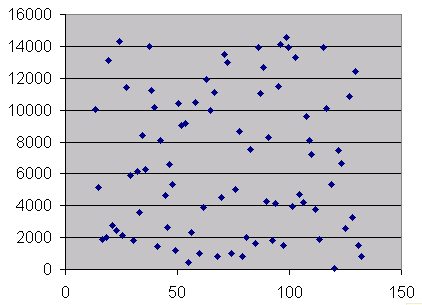

- Après avoir observé le graphique, vous pouvez utiliser la fonction CORREL. Dans notre exemple, la fonction s’écrirait : CORREL(A2:A83,B2:B83). Si le résultat est proche de 0, alors la corrélation est faible, et la conclusion est : il n’existe tout simplement aucune tendance réelle. Si elle est proche de 1, alors la corrélation est forte. Ce dernier point est utile, puisqu’il augmente le pouvoir explicatif de la relation que vous avez trouvée.
Il existe des méthodes plus subtiles pour s’assurer que la corrélation est élevée ; nous y reviendrons plus tard.
Bien sûr, ces dernières étapes peuvent être automatisées : vous n’avez pas besoin de noter la relation et d’utiliser votre calculatrice de poche pour effectuer le calcul. Vous avez besoin de l’Analysis Toolpak!
Prévision à l’aide de l’Analysis Toolpak
Avant de continuer, vous devriez vérifier si le Excel ATP (Analysis Toolpak) est installé. Reportez-vous à la section Installation de l’Analysis Toolpak pour plus d’informations.
Malheureusement, des données de ventes aussi parfaites, avec une relation linéaire aussi agréable et simple, sont assez rares dans la réalité. Voyons ce qu’Excel a à offrir pour des situations plus compliquées, avec des données plus complexes.
Aller plus loin : l’exemple de l’ajustement exponentiel
Comme vous pouvez l’imaginer, un modèle linéaire de vos données n’est pas toujours probable. En fait, il y a de nombreuses raisons de croire qu’il devrait suivre un modèle exponentiel. De nombreux comportements dans l’économie sont régis par des équations exponentielles (par exemple, le calcul de la capitalisation des intérêts en est un exemple classique).
Voici comment réaliser un ajustement exponentiel :
- Regardez vos données. Tracez un graphique simple, et observez-le. Si elles suivent une évolution exponentielle, elles devraient ressembler à ceci :
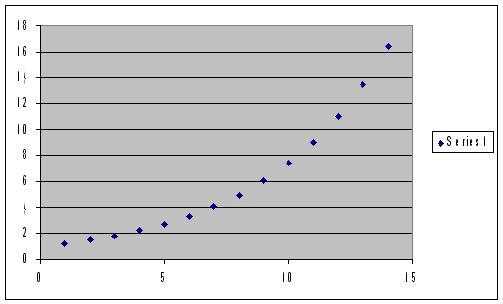
C’est le cas idéal. Bien sûr, les données ne ressembleront jamais exactement à cela. Mais si les points semblent suivre approximativement cette répartition, cela devrait vous encourager à envisager un ajustement exponentiel.

Comme dans l’exemple précédent, vous pouvez toujours tracer un graphique de vos données, demander une courbe de tendance, et choisir « exponential » au lieu de « linear ». Ensuite, notez l’équation affichée, comme d’habitude.
- Heureusement, vous pouvez également faire tout cela directement, en utilisant l’Analysis Toolpak : mettez toutes vos données dans une feuille Excel vierge, et allez dans Outils => Analyse de données
Installation de l’Analysis Toolpak (ATP)
L’ATP est un complément fourni avec Microsoft Excel, mais il n’est pas toujours installé par défaut. Pour l’installer, vous pouvez procéder comme suit :
- Assurez-vous d’avoir votre CD Office à portée de main. Excel pourrait vous demander d’insérer le CD afin d’installer les fichiers de l’ATP.
- Ouvrez une feuille Excel, allez dans le menu Outils, puis sélectionnez Compléments. Cochez la première case de la fenêtre, intitulée « 2.Analysis Toolpak ».
- Insérez votre CD Office si le logiciel vous le demande.
- Voilà ! Notez que votre menu « Tools » inclut désormais beaucoup plus de fonctionnalités, notamment une option « Data Analysis ». C’est celle que nous utiliserons le plus.
Utilisation de l’Analysis Toolpak (ATP)
… en mode linéaire
Revenons maintenant à notre exemple linéaire. Si vos données « ont l’air » bonnes (voir l’illustration ci-dessus), vous pouvez utiliser l’ATP pour obtenir une estimation directe de la forme fonctionnelle, sans passer par le processus de « trendline ».
Ouvrez votre feuille de données, puis ouvrez le menu « Tools » et sélectionnez « Data Analysis ». Une fenêtre apparaît, vous demandant quel type d’analyse vous souhaitez effectuer. Sélectionnez « regression » pour un réglage linéaire.
Vous devez maintenant fournir deux arguments à Excel : une plage « Y » et une plage « X ». La plage Y indique ce que vous souhaitez estimer (c’est-à-dire vos ventes), et la plage X contient les données que vous pensez pouvoir expliquer vos ventes (ici, votre coût unitaire). Dans notre exemple (voir example1.xls), nos données de ventes se trouvent dans la colonne B, de la ligne 3 à la ligne 90. Vous devez donc mettre « $B$3:$B$90 » comme plage Y, et « $A$3:$A$90 » comme plage X. Une fois terminé, cliquez sur « ok ».
Une nouvelle feuille apparaît, contenant les « résultats de régression ».
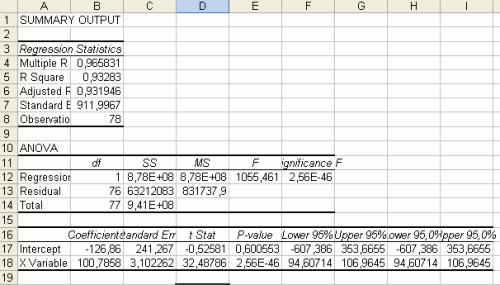
Le résultat le plus important se trouve dans la colonne « Coefficients » au bas de la feuille. L’ordonnée à l’origine est la constante, et le coefficient de la « variable X » est le coefficient de X (ici, votre coût unitaire). Ainsi, nous trouvons la même équation que celle obtenue en utilisant la fonction « trendline ». Ventes = Intercept + coefficient de X * coût unitaire, soit : -126 + 100 * coût unitaire
Cette feuille contient également un nombre utile qui vous renseigne sur la qualité de votre estimation : le « R Square ». S’il est proche de 1, alors votre estimation est bonne, ce qui signifie que l’équation trouvée représente assez bien vos données. S’il est proche de 0, alors l’estimation n’est pas bonne, et vous devriez probablement essayer un autre type d’ajustement (voir l’ajustement exponentiel ci-dessous).
Cette méthode est probablement plus rapide que les techniques de « trendline ». Cependant, elle est un peu plus technique et beaucoup moins visuelle. Donc, si vous ne souhaitez pas vous embêter à tracer et examiner visuellement vos données, assurez-vous au moins de vérifier la valeur du « R square ».
… en utilisant l’ajustement exponentiel
Si l’estimation linéaire ne fonctionne pas bien (par exemple, si vous obtenez un faible R-Squared, c’est-à-dire 0,1), vous pourriez vouloir utiliser l’ajustement exponentiel.
Lancez l’Analysis Toolpak, comme d’habitude : ouvrez votre feuille de données, puis ouvrez le menu « Tools » et sélectionnez « Data Analysis ». Une fenêtre apparaît, vous demandant quel type d’analyse vous souhaitez réaliser.
Dans notre configuration exponentielle, ce que nous souhaitons sélectionner est « exponential ».
Notez qu’Excel ne vous demande qu’une seule plage d’entrée. Sélectionnez la colonne qui contient les données que vous souhaitez prévoir (c’est-à-dire le coût unitaire), et choisissez un “smoothing factor”.
Comment savoir quel modèle choisir ?
Notez que vous n’avez pas besoin d’essayer chaque méthode d’estimation afin de trouver celle qui fonctionne le mieux pour vous. Cela ne peut être réalisé que par l’automatisation, car il existe un très grand nombre de méthodes disponibles. Si vous souhaitez que tous les modèles soient évalués par rapport à vos données, vous pouvez envisager de les envoyer à Lokad. Nous disposons d’un système informatique puissant qui « teste » tous les modèles et sélectionne uniquement ceux qui fonctionnent le mieux avec les données de votre entreprise.