Berechne den Callcenter-Personaleinsatz mit Excel

This guide explains how to optimize the number of agents to reach the desired service level. This guide applies to call centers and contact centers. The theory is illustrated with Microsoft Excel. Advanced notes are available for software developer who would like to reproduce the theory into a custom application.

Download: erlang-by-lokad.xls (Microsoft Excel-Tabelle)

When opening the spreadsheet, Excel will warn you than this document contains macros. Those macros correspond to the Erlang-C formula (see explanation below). You need to activate the macros in order to reproduce the calculations.

Modellierung der eingehenden Anrufaktivität

Die eingehende Anrufaktivität kann mit wenigen Variablen modelliert werden:

• Die durchschnittliche Anrufdauer, bezeichnet mit t, ist bekannt. t befindet sich in B7.
• Die Anzahl der Agenten, bezeichnet mit m, ist bekannt. m befindet sich in B8.
• Die Anrufankunftsrate, bezeichnet mit λ, ist bekannt. Die Ankunftsrate ist die Anzahl der eingehenden Anrufe pro Sekunde. In der Arbeitsmappe befindet sich λ in B9.

Im Folgenden werden wir auf Grundlage dieser 3 Variablen sowie einiger statistischer Annahmen in der Lage sein, zu berechnen

• die durchschnittliche Auslastung der Agenten.
• die Wahrscheinlichkeit, dass ein Anruf warten muss.
• die Wahrscheinlichkeit, dass ein Anruf länger als eine bestimmte Zeit warten muss.

Die wichtigste statistische Annahme ist, dass die eingehenden Anrufe sich statistisch wie ein Poisson-Prozess verhalten. Ohne zu sehr ins Detail zu gehen, ist diese Annahme vernünftig, wenn die Anrufereignisse größtenteils unabhängig sind.

Gegenbeispiel: Wenn wir den Fall eines Callcenters betrachten, das Anrufe von Zuschauern erhält, die versuchen, eine Frage bei einer Fernsehsendung zu beantworten, dann wird die Poisson-Annahme offensichtlich nicht zutreffen, da alle Anrufe gleichzeitig durch dasselbe Ereignis (die Fernsehsendung) ausgelöst werden.

Berechnung von Kennzahlen mit Erlang

Auf Grundlage der in der vorherigen Sektion eingeführten Annahmen werden wir nun ein paar aufschlussreiche Kennzahlen berechnen, die die Aktivität im Callcenter widerspiegeln.

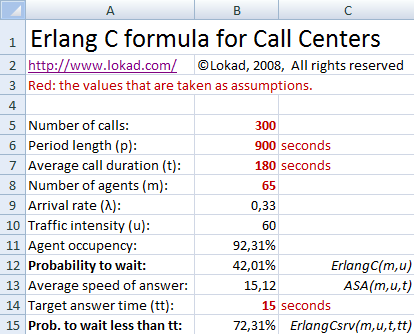
Die Periodenlänge stellt die Dauer des betrachteten Zeitfensters dar. In der obigen Abbildung beträgt sie 900s, das heißt 15 Minuten, ein in Callcentern sehr häufig verwendetes Aggregationsniveau.

Die Verkehrsintensität ist eine Zahl, die die minimale Anzahl an Agenten repräsentiert, die benötigt wird, um alle eingehenden Anrufe zu bearbeiten. Wenn weniger Agenten vorhanden sind als die Verkehrsintensität, werden mechanisch Anrufe abgewiesen. Die Verkehrsintensität wird u genannt und als Produkt der Anrufankunftsrate λ und der durchschnittlichen Anrufdauer t berechnet. In der Arbeitsmappe wird die Verkehrsintensität in B10 berechnet.

Die durchschnittliche Auslastung der Agenten (oder Utilisierung) ist ein Verhältnis, das den Anteil der Zeit ausdrückt, in der die Agenten tatsächlich Anrufe beantworten, im Vergleich zur Gesamtzeit (die auch Leerlaufzeiten beinhalten kann). Die Agentenauslastung kann einfach berechnet werden, indem man die Verkehrsintensität u durch die Anzahl der Agenten m teilt. In der Arbeitsmappe wird die Agentenauslastung in B11 berechnet.

Die Wartewahrscheinlichkeit (aus Sicht des Anrufers) drückt die Wahrscheinlichkeit aus, dass ein Agent sofort verfügbar (d.h. in Bereitschaft) ist, um einen eingehenden Anruf zu beantworten. Dieser Wert wird durch die Erlang-C-Formel ermittelt – leider geht die Detailgenauigkeit der Erlang-C-Formel über den Rahmen dieses Leitfadens hinaus¹. In der Beispiel-Arbeitsmappe wird die Wartewahrscheinlichkeit in B12 mittels der in Visual Basic implementierten ErlangC-Makrofunktion berechnet. Die ErlangC-Funktion nimmt zwei Argumente: erstens m, die Anzahl der Agenten, und zweitens u, die Verkehrsintensität.

Die durchschnittliche Antwortzeit (ASA) stellt die durchschnittliche Wartezeit eines Anrufes dar. Die Berechnung der ASA basiert auf der Erlang-C-Formel. In der Beispiel-Arbeitsmappe wird die ASA in B13 mithilfe der in Visual Basic implementierten ASA-Makrofunktion berechnet. Die ASA-Funktion nimmt drei Argumente: erstens m, die Anzahl der Agenten, zweitens u und drittens t, die durchschnittliche Anrufdauer.

Die Wahrscheinlichkeit, weniger als eine Zielwartezeit zu haben, ist selbsterklärend. Wie bei der Wartewahrscheinlichkeit gehen die Details der eigentlichen Formel über den Rahmen dieses Leitfadens hinaus. In der Beispiel-Arbeitsmappe wird die Wahrscheinlichkeit in B15 berechnet, wobei die gewünschte Wartezeit (d.h. Zielwartezeit), bezeichnet als tt, in B14 angegeben wird. Die Berechnung erfolgt mittels der Funktion ErlangCsrv, die vier Argumente entgegennimmt: erstens m, die Anzahl der Agenten, zweitens u, die Verkehrsintensität, drittens t, die durchschnittliche Anrufdauer, und viertens tt, die Zielwartezeit.

Praktische Personalplanung mit Excel

In den vorangegangenen Abschnitten haben wir gesehen, wie man nützliche Kennzahlen zur Analyse der Callcenter-Aktivität berechnet. Allerdings wurde das Excel-Layout (siehe Screenshot oben) der Übersichtlichkeit halber gewählt und ist nicht für eine praktische Callcenter-Personalplanung geeignet.

In diesem Abschnitt schlagen wir vor, ein wesentlich kompakteres Layout zu verwenden, wie im folgenden Screenshot dargestellt.

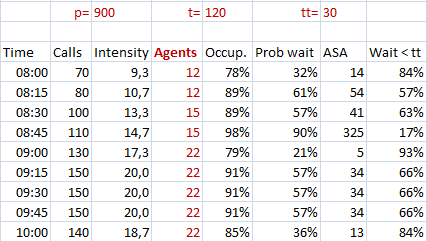
In der Beispiel-Arbeitsmappe befindet sich die obere linke Ecke der obigen Abbildung in der Zelle E2 (die Zelle ist leer). Die in dieser Tabelle durchgeführten Berechnungen sind lediglich die direkte Anwendung der in der vorherigen Sektion vorgestellten Formeln.

Ein paar Anmerkungen

• Es wird von einer konstanten durchschnittlichen Anrufdauer t und einer konstanten Zielwartezeit tt ausgegangen.
• Wir verwenden statische Excel-Zellbezüge, d.h. $A$1 statt A1 für die Variablen (was das Kopieren und Einfügen der Formeln erleichtert).
• Die Anzahl der Agenten kann frei optimiert werden, um die erwarteten Service-Levels anzupassen.
• Die Zellenformatierung ist so angepasst, dass nicht zu viele Dezimalstellen angezeigt werden.

Lizenz

Hiermit wird jeder Person, die eine Kopie dieser Software und der zugehörigen Dokumentationsdateien (die “Software”) erhält, kostenlos die Erlaubnis erteilt, uneingeschränkt mit der Software zu verfahren, einschließlich der unbeschränkten Rechte, sie zu benutzen, zu kopieren, zu modifizieren, zusammenzuführen, zu veröffentlichen, zu verbreiten, unterzulizenzieren und/oder Kopien der Software zu verkaufen, und Personen, denen die Software zur Verfügung gestellt wird, dies zu gestatten, vorbehaltlich der folgenden Bedingungen:

Der obige Copyright-Hinweis und diese Genehmigungserklärung müssen in allen Kopien oder wesentlichen Teilen der Software enthalten sein.

DIE SOFTWARE WIRD OHNE JEDE GEWÄHRLEISTUNG ZUR VERFÜGUNG GESTELLT, WEDER AUSDRÜCKLICH NOCH STILLSCHWEIGEND, EINSCHLIESSLICH, ABER NICHT BESCHRÄNKT AUF DIE GEWÄHRLEISTUNG DER MARKTGÄNGIGKEIT, EIGNUNG FÜR EINEN BESTIMMTEN ZWECK UND NICHTVERLETZUNG. IN KEINEM FALL HAFTEN DIE AUTOREN ODER COPYRIGHTINHABER FÜR ANSPRÜCHE, SCHÄDEN ODER SONSTIGE HAFTUNG, OB AUS VERTRAG, UNERLAUBTER HANDLUNG ODER ANDERWEITIG, DIE AUS ODER IM ZUSAMMENHANG MIT DER SOFTWARE ODER DER NUTZUNG ODER SONSTIGEN GESCHÄFTEN MIT DER SOFTWARE ENTSTEHEN.

Hinweise