Generalisierung (Prognostizieren)
Generalisierung ist die Fähigkeit eines Algorithmus, ein Modell – unter Ausnutzung eines Datensatzes – zu erstellen, das auch auf zuvor ungesehenen Daten gut funktioniert. Generalisierung ist von entscheidender Bedeutung für supply chain, da die meisten Entscheidungen eine Erwartung der Zukunft widerspiegeln. Im Kontext der Prognose sind die Daten ungesehen, weil das Modell zukünftige Ereignisse vorhersagt, die nicht beobachtbar sind. Während seit den 1990er Jahren sowohl theoretisch als auch praktisch beachtliche Fortschritte im Bereich der Generalisierung erzielt wurden, bleibt wahre Generalisierung schwer fassbar. Die vollständige Lösung des Generalisierungsproblems dürfte der des Problems der künstlichen allgemeinen Intelligenz nicht allzu sehr ähneln. Darüber hinaus bringt supply chain noch eine Vielzahl eigenständiger, kniffliger Probleme neben den herkömmlichen Herausforderungen der Generalisierung mit sich.
Übersicht über ein Paradoxon
Ein Modell zu erstellen, das auf den vorliegenden Daten perfekt funktioniert, ist einfach: Es genügt, den Datensatz vollständig auswendig zu lernen und ihn dann zu nutzen, um jede Anfrage bezüglich des Datensatzes zu beantworten. Da Computer große Datensätze effizient speichern können, ist es leicht, ein solches Modell zu entwickeln. Allerdings ist dies in der Regel auch sinnlos1, da der eigentliche Zweck eines Modells in seiner prognostischen Fähigkeit über das bereits Beobachtete hinausliegt.
Ein scheinbar unausweichliches Paradoxon tritt zutage: Ein gutes Modell ist eines, das mit Daten, die derzeit nicht verfügbar sind, gut funktioniert, aber per Definition, wenn die Daten nicht verfügbar sind, kann der Beobachter die Bewertung nicht vornehmen. Der Begriff „Generalisierung“ bezieht sich daher auf die schwer fassbare Fähigkeit bestimmter Modelle, ihre Relevanz und Qualität über die zum Zeitpunkt der Modellerstellung verfügbaren Beobachtungen hinaus beizubehalten.
Obwohl das Auswendiglernen der Beobachtungen als unzureichende Modellierungsstrategie abgetan werden kann, ist jede alternative Methode zur Erstellung eines Modells potenziell demselben Problem ausgesetzt. Unabhängig davon, wie gut das Modell mit den derzeit verfügbaren Daten zu funktionieren scheint, ist es immer denkbar, dass dies nur ein Zufall ist oder, schlimmer noch, ein Defekt der Modellierungsstrategie. Was zunächst als ein Randphänomen eines statistischen Paradoxons erscheint, ist in Wirklichkeit ein weitreichendes Problem.
Als anekdotischer Beleg führte die SEC (Securities and Exchange Commission), die US-Behörde, die für die Regulierung der Kapitalmärkte zuständig ist, im Jahr 1979 ihre berühmte Rule 156 ein. Diese Regel verlangt von Fondsmanagern, die Investoren darauf hinzuweisen, dass die vergangene Leistung keine Aussage über zukünftige Ergebnisse trifft. Die vergangene Leistung ist implizit das „Modell“, dessen „Generalisierungsfähigkeit“ die SEC davor warnt zu vertrauen; das heißt, seine Fähigkeit, etwas über die Zukunft auszusagen.
Selbst die Wissenschaft hat Schwierigkeiten damit, was es bedeutet, die „Wahrheit“ außerhalb eines engen Beobachtungsbereichs zu extrapolieren. Die „Bad-Science“-Skandale, die sich in den 2000er und 2010er Jahren rund um p-hacking ereigneten, deuten darauf hin, dass ganze Forschungsbereiche fehlerhaft sind und nicht vertraut werden kann2. Obwohl es Fälle von offenkundigem Betrug gibt, bei denen die experimentellen Daten offensichtlich manipuliert wurden, liegt der Kern des Problems meist in den Modellen; das heißt, im intellektuellen Prozess, der angewandt wird, um das Beobachtete zu generalisieren.
In seiner weitreichendsten Form ist das Generalisierungsproblem nicht von dem der Wissenschaft selbst zu unterscheiden, weshalb es ebenso schwierig ist wie die Nachahmung der gesamten Bandbreite menschlicher Genialität und Potenzial. Dennoch ist die engere statistische Ausprägung des Generalisierungsproblems weitaus zugänglicher, und aus dieser Perspektive wird in den folgenden Abschnitten vorgegangen.
Das Aufkommen einer neuen Wissenschaft
Als statistisches Paradigma entstand Generalisierung zu Beginn des 20. Jahrhunderts, vor allem durch die Brille der Prognosegenauigkeit3, welche einen speziellen Fall darstellt, der eng mit Zeitreihen verknüpft ist. In den frühen 1900er Jahren entfachte das Aufkommen einer börsennotierten Mittelschicht in den USA ein enormes Interesse an Methoden, die den Menschen helfen sollten, finanzielle Erträge aus ihren gehandelten Vermögenswerten zu sichern. Wahrsager und Wirtschaftsprognostiker unternahmen gleichermaßen den Versuch, zukünftige Ereignisse zu extrapolieren. Wohlstand wurde gemacht und verloren, aber diese Bemühungen warfen nur wenig Licht auf die „richtige“ Herangehensweise an das Problem.
Generalisierung blieb weitgehend ein rätselhaftes Problem für den größten Teil des 20. Jahrhunderts. Es war nicht einmal klar, ob es in den Bereich der Naturwissenschaften gehörte, der von Beobachtungen und Experimenten bestimmt wird, oder in den Bereich der Philosophie und Mathematik, der von Logik und Selbstkonsistenz geprägt ist.
Der Ablauf zog sich hin, bis zu einem Wendepunkt im Jahr 1982, dem Jahr des ersten öffentlichen Prognosewettbewerbs – umgangssprachlich als der M-Wettbewerb4 bekannt. Das Prinzip war einfach: Man veröffentlicht einen Datensatz von 1000 abgeschnittenen Zeitreihen, lässt Teilnehmer ihre Prognosen einsenden und veröffentlicht schließlich den Rest des Datensatzes (die abgeschnittenen Enden) zusammen mit den von den Teilnehmern erzielten Genauigkeiten. Durch diesen Wettbewerb hatte Generalisierung, noch betrachtet durch die Brille der Prognosegenauigkeit, den Bereich der Naturwissenschaften erreicht. Zukünftig wurden Prognosewettbewerbe immer häufiger.
Einige Jahrzehnte später fügte Kaggle, gegründet im Jahr 2010, solchen Wettbewerben eine neue Dimension hinzu, indem es eine Plattform für allgemeine Vorhersageprobleme (nicht nur Zeitreihen) schuf. Ab Februar 20235 hat die Plattform 349 Wettbewerbe mit Geldpreisen organisiert. Das Prinzip bleibt dasselbe wie beim ursprünglichen M-Wettbewerb: Ein abgeschnittener Datensatz wird zur Verfügung gestellt, die Teilnehmer reichen ihre Antworten zu den vorgegebenen Vorhersageaufgaben ein und schließlich werden die Ranglisten zusammen mit dem verborgenen Teil des Datensatzes enthüllt. Die Wettbewerbe gelten immer noch als Goldstandard für die korrekte Bewertung des Generalisierungsfehlers von Modellen.
Overfitting und Underfitting
Overfitting, wie auch sein antonymes underfitting, ist ein Problem, das häufig bei der Erstellung eines Modells auf Basis eines gegebenen Datensatzes auftritt und die Generalisierungsfähigkeit des Modells untergräbt. Historisch6 trat Overfitting als das erste gut verstandene Hindernis für die Generalisierung auf.
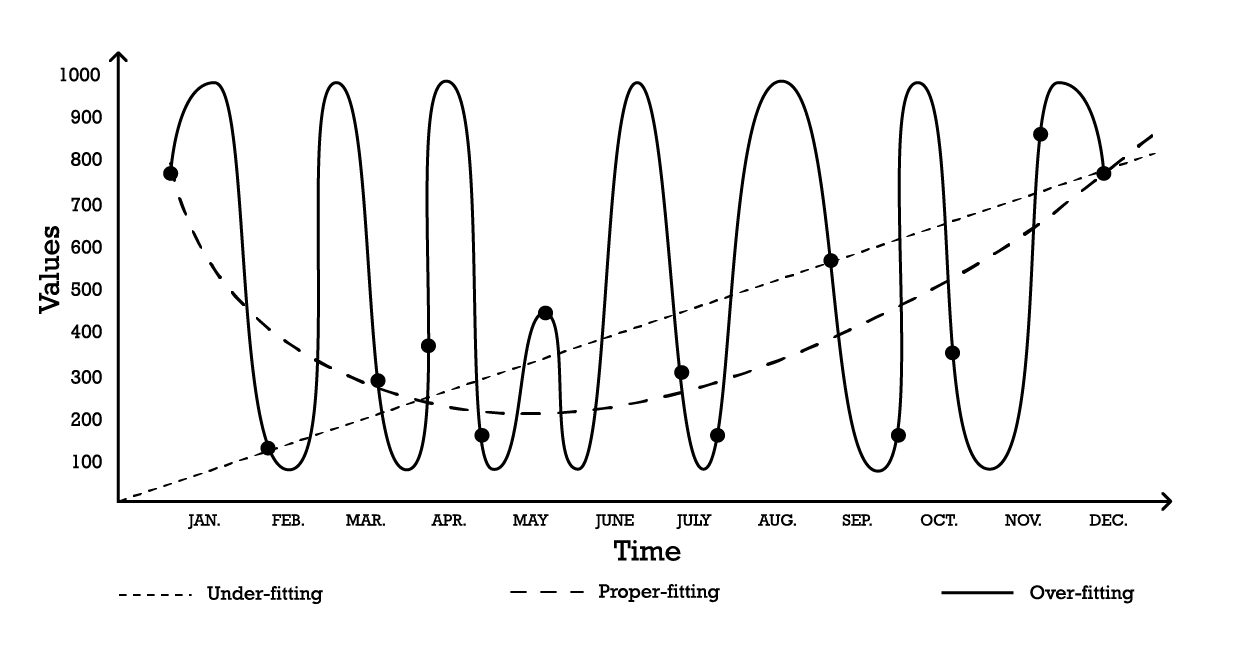
Die Visualisierung von Overfitting kann anhand eines einfachen Zeitreihen-Modellierungsproblems erfolgen. Für dieses Beispiel nehmen wir an, dass das Ziel darin besteht, ein Modell zu erstellen, das einer Reihe historischer Beobachtungen entspricht. Eine der einfachsten Möglichkeiten, diese Beobachtungen zu modellieren, ist ein lineares Modell, wie unten veranschaulicht (siehe Abbildung 1).

Abbildung 1: Ein zusammengesetztes Diagramm, das drei verschiedene Versuche zeigt, eine Reihe von Beobachtungen anzupassen.
Mit zwei Parametern ist das „under-fitting“ Modell robust, passt sich jedoch, wie der Name schon andeutet, underfits den Daten nicht an, da es eindeutig versagt, die Gesamtform der Verteilung der Beobachtungen zu erfassen. Dieser lineare Ansatz weist einen hohen Bias, aber eine geringe Varianz auf. In diesem Zusammenhang sollte Bias als die inhärente Einschränkung der Modellierungsstrategie verstanden werden, die feine Details der Beobachtungen einzufangen, während Varianz als die Empfindlichkeit gegenüber kleinen Schwankungen – möglicherweise Rauschen – in den Beobachtungen zu verstehen ist.
Ein ziemlich komplexes Modell könnte gewählt werden, entsprechend der „over-fitting“ Kurve (Abbildung 1). Dieses Modell umfasst viele Parameter und passt exakt zu den Beobachtungen. Dieser Ansatz weist einen niedrigen Bias, aber eine nachweislich hohe Varianz auf. Alternativ könnte ein Modell mittlerer Komplexität gewählt werden, wie in der „proper-fitting“ Kurve (Abbildung 1) zu sehen ist. Dieses Modell umfasst drei Parameter, hat einen mittleren Bias und eine mittlere Varianz. Von diesen drei Optionen erweist sich das proper-fitting Modell stets als dasjenige, das in Bezug auf die Generalisierung am besten abschneidet.
Diese Modellierungsoptionen repräsentieren das Wesen des Bias-Varianz-Trade-offs.7 8 Der Bias-Varianz-Trade-off ist ein allgemeines Prinzip, das besagt, dass der Bias durch eine Erhöhung der Varianz reduziert werden kann. Der Generalisierungsfehler wird minimiert, indem das richtige Gleichgewicht zwischen dem Maß an Bias und Varianz gefunden wird.
Historisch gesehen wurde von den frühen 1900er Jahren bis in die frühen 2010er ein überangepasstes Modell9 als eines definiert, das mehr Parameter enthält, als durch die Daten gerechtfertigt werden können. Tatsächlich erscheint es auf den ersten Blick so, als wäre das Hinzufügen zu vieler Freiheitsgrade das perfekte Rezept für Overfitting-Probleme. Doch das Aufkommen von deep learning erwies diese Intuition – und die Definition von Overfitting – als irreführend. Dieser Punkt wird im Abschnitt über deep double-descent nochmals aufgegriffen.
Kreuzvalidierung und Backtesting
Die Kreuzvalidierung ist eine Methode zur Modellvalidierung, die dazu dient, zu beurteilen, wie gut ein Modell über den unterstützenden Datensatz hinaus generalisiert. Es handelt sich um eine Subsampling-Methode, bei der in verschiedenen Iterationen unterschiedliche Teile der Daten zum Testen und Trainieren eines Modells verwendet werden. Kreuzvalidierung ist das A und O moderner Vorhersagepraktiken, und nahezu alle Sieger von Vorhersagewettbewerben nutzen sie umfangreich.
Es gibt zahlreiche Varianten der Kreuzvalidierung. Die beliebteste Variante ist die k-fache Validierung, bei der die ursprüngliche Stichprobe zufällig in k Teilstichproben aufgeteilt wird. Jede Teilstichprobe wird einmal als Validierungsdaten verwendet, während der Rest – alle anderen Teilstichproben – als Trainingsdaten dient.
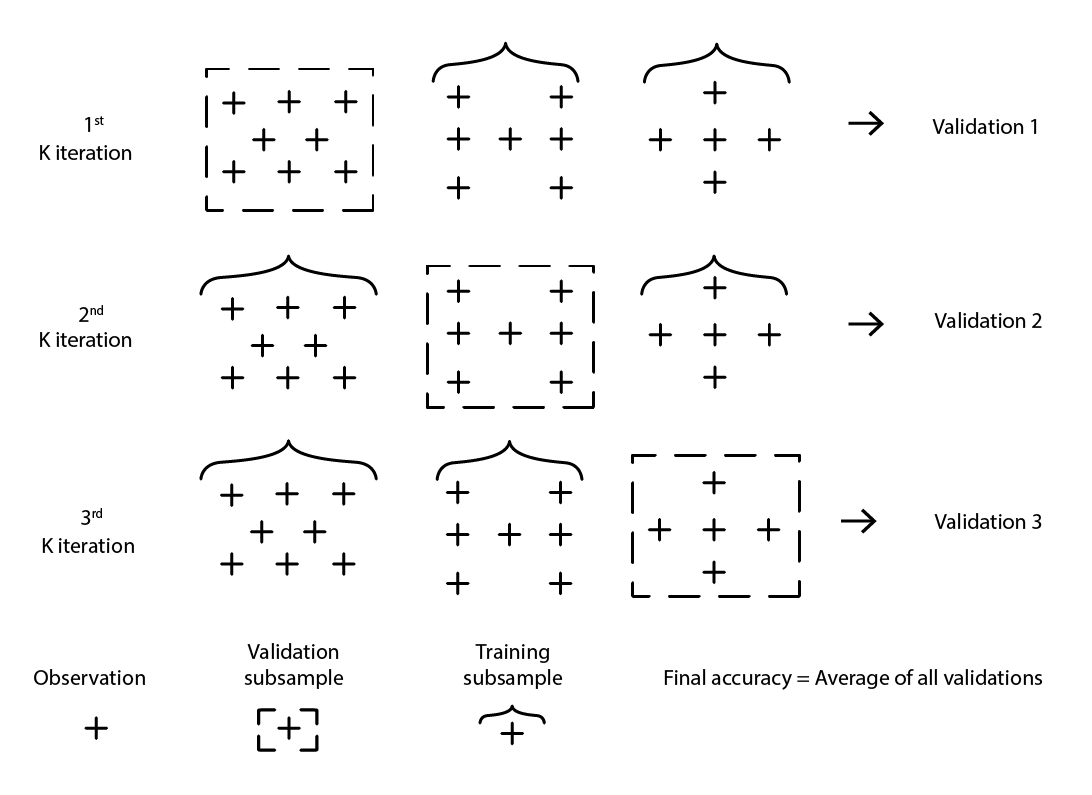
Abbildung 2: Eine Beispiel-K-fache Validierung. Die obigen Beobachtungen stammen alle aus demselben Datensatz. Die Technik erstellt damit Datenteilstichproben für Validierungs- und Trainingszwecke.
Die Wahl des Wertes k, also der Anzahl der Teilstichproben, ist ein Kompromiss zwischen marginalen statistischen Gewinnen und den Anforderungen an die Rechenressourcen. Tatsächlich steigen bei der k-fachen Validierung die benötigten Ressourcen linear mit dem Wert k, während die Vorteile in Form von Fehlerreduktion extreme abnehmende Erträge verzeichnen10. In der Praxis erweist sich die Auswahl eines Wertes von 10 oder 20 für k in der Regel als „gut genug“, da die mit höheren Werten verbundenen statistischen Gewinne den zusätzlichen Aufwand an Rechenressourcen nicht rechtfertigen.
Die Kreuzvalidierung geht davon aus, dass der Datensatz in eine Reihe unabhängiger Beobachtungen zerlegt werden kann. In supply chain ist dies jedoch häufig nicht der Fall, da der Datensatz in der Regel eine Art historisierte Daten widerspiegelt, bei denen eine Zeitabhängigkeit vorhanden ist. In Anwesenheit von Zeit muss sichergestellt werden, dass die Trainings-Teilstichprobe streng „vor“ der Validierungsstichprobe liegt. Mit anderen Worten, die „Zukunft“ relativ zum Resampling-Schnittpunkt darf nicht in die Validierungsstichprobe eindringen.
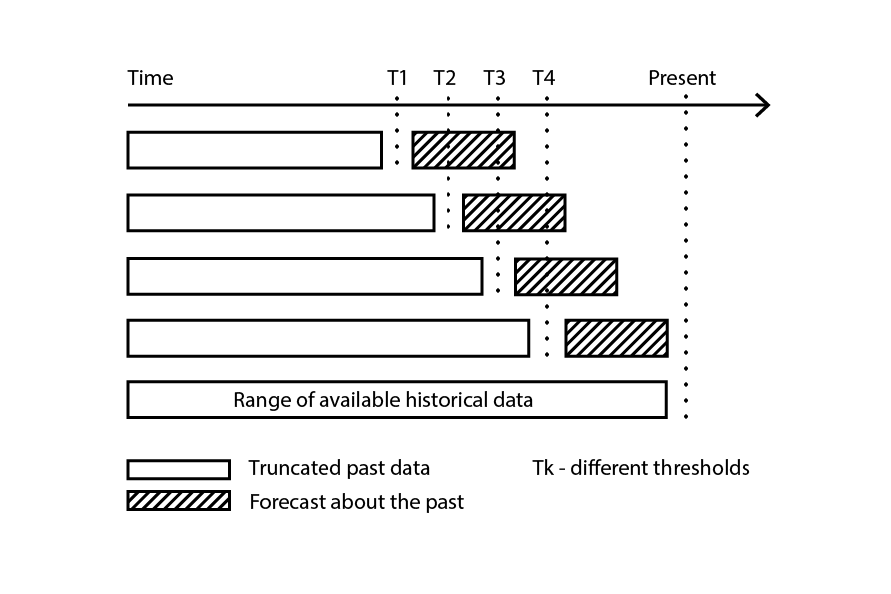
Abbildung 3: Ein Beispielprozess des Backtestings, der Datenteilstichproben für Validierungs- und Trainingszwecke erstellt.
Backtesting stellt die Variante der Kreuzvalidierung dar, die direkt die Zeitabhängigkeit berücksichtigt. Anstatt zufällige Teilstichproben zu betrachten, werden Trainings- und Validierungsdaten jeweils durch einen Schnittpunkt bestimmt: Beobachtungen vor dem Schnittpunkt gehören zu den Trainingsdaten, während Beobachtungen nach dem Schnittpunkt zu den Validierungsdaten gehören. Dieser Prozess wird durch Auswahl einer Reihe unterschiedlicher Schnittpunkte wiederholt.
Die Resampling-Methode, die sowohl der Kreuzvalidierung als auch dem Backtesting zugrunde liegt, ist ein mächtiger Mechanismus, um die Modellierungsbemühungen in Richtung einer besseren Generalisierung zu lenken. Tatsächlich ist sie so effizient, dass es eine ganze Klasse von (Machine) Learning-Algorithmen gibt, die diesen Mechanismus in ihrem Kern integriert haben. Die bekanntesten davon sind Random Forests und Gradient Boosted Trees.
Durchbrechen der Dimensionsbarriere
Ganz natürlich: Je mehr Daten zur Verfügung stehen, desto mehr Informationen können daraus gewonnen werden. Folglich sollten, bei sonst gleichen Bedingungen, mehr Daten zu besseren Modellen führen oder zumindest zu Modellen, die nicht schlechter sind als ihre Vorgänger. Schließlich, wenn zusätzliche Daten das Modell verschlechtern würden, könnte man sie immer als letzten Ausweg ignorieren. Doch aufgrund von Overfitting-Problemen blieb das Verwerfen von Daten bis Ende der 1990er Jahre das kleinere Übel. Dies war der Kern des Problems der „Dimensionsbarriere“. Diese Situation war sowohl verwirrend als auch zutiefst unbefriedigend. Durchbrüche in den 1990er Jahren durchbrachen die Dimensionsbarrieren mit atemberaubenden theoretischen und praktischen Einsichten. Dabei gelang es diesen Durchbrüchen, – durch reine Ablenkungswirkung – das gesamte Forschungsfeld über ein Jahrzehnt hinweg aus der Bahn zu werfen und den Eintritt ihrer Nachfolger, hauptsächlich Deep Learning-Methoden, zu verzögern, wie im nächsten Abschnitt erörtert wird.
Um besser zu verstehen, was früher daran falsch war, mehr Daten zu haben, betrachten Sie folgendes Szenario: Ein fiktiver Hersteller möchte die Anzahl ungeplanter Reparaturen pro Jahr an großen Industrieanlagen vorhersagen. Nach sorgfältiger Betrachtung des Problems hat das Ingenieurteam drei unabhängige Faktoren identifiziert, die scheinbar zu den Ausfallraten beitragen. Allerdings ist der jeweilige Beitrag jedes Faktors zur Gesamtausfallrate unklar.
Daher wird ein einfaches lineares Regressionsmodell mit 3 Eingangsvariablen eingeführt. Das Modell kann geschrieben werden als Y = a1 * X1 + a2 * X2 + a3 * X3, wobei
-
Y ist der Output des linearen Modells (die Ausfallrate, die die Ingenieure vorhersagen möchten)
-
X1, X2 und X3 sind die drei Faktoren (spezifische Arten von Arbeitsbelastungen, ausgedrückt in Betriebsstunden), die zu den Ausfällen beitragen können
Die Anzahl der Beobachtungen, die benötigt werden, um „gut genug“ Schätzungen für die drei Parameter zu erhalten, hängt weitgehend vom Rauschpegel in der Beobachtung ab und davon, was als „gut genug“ gilt. Intuitiv betrachtet wären jedoch mindestens zwei Dutzend Beobachtungen erforderlich, um drei Parameter anzupassen, selbst unter den günstigsten Umständen. Da es den Ingenieuren gelingt, 100 Beobachtungen zu sammeln, regressieren sie erfolgreich 3 Parameter, und das resultierende Modell erscheint als „gut genug“, um von praktischem Interesse zu sein. Das Modell erfasst viele Aspekte der 100 Beobachtungen nicht, was es zu einer sehr groben Annäherung macht, aber wenn dieses Modell durch Gedankenexperimente mit anderen Situationen konfrontiert wird, sagen Intuition und Erfahrung den Ingenieuren, dass sich das Modell vernünftig verhält.
Aufbauend auf ihrem ersten Erfolg entscheiden sich die Ingenieure, tiefer zu forschen. Dieses Mal nutzen sie die gesamte Bandbreite an elektronischen Sensoren, die in die Maschinen eingebettet sind, und durch die von diesen Sensoren erzeugten elektronischen Aufzeichnungen gelingt es ihnen, die Menge der Eingangsgrößen auf 10.000 zu erhöhen. Ursprünglich bestand der Datensatz aus 100 Beobachtungen, wobei jede Beobachtung durch 3 Zahlen charakterisiert war. Nun wurde der Datensatz erweitert; es sind immer noch dieselben 100 Beobachtungen, aber jede Beobachtung enthält 10.000 Zahlen.
Doch als die Ingenieure versuchen, denselben Ansatz auf ihren stark erweiterten Datensatz anzuwenden, funktioniert das lineare Modell nicht mehr. Da es 10.000 Dimensionen gibt, kommt das lineare Modell mit 10.000 Parametern daher, und die 100 Beobachtungen reichen bei Weitem nicht aus, um so viele Parameter zu regressieren. Das Problem ist nicht, dass es unmöglich sei, passende Parameterwerte zu finden, sondern genau das Gegenteil: Es ist trivial geworden, unendlich viele Parametersätze zu finden, die die Beobachtungen perfekt anpassen. Dennoch ist keines dieser „passenden“ Modelle praktisch nützlich. Diese „großen“ Modelle passen die 100 Beobachtungen zwar perfekt an, werden aber außerhalb dieser Beobachtungen unsinnig.
Die Ingenieure stehen vor der Dimensionsbarriere: Offensichtlich muss die Anzahl der Parameter im Vergleich zu den Beobachtungen klein bleiben, sonst zerfällt der Modellierungsansatz. Dieses Problem ist ärgerlich, da der „größere“ Datensatz mit 10.000 Dimensionen statt 3 offensichtlich informativer ist als der kleinere. Daher sollte ein korrektes statistisches Modell in der Lage sein, diese zusätzliche Information zu erfassen, anstatt funktionsuntüchtig zu werden, wenn es damit konfrontiert wird.
Mitte der 1990er-Jahre führte ein zweifacher Durchbruch11 – sowohl theoretisch als auch experimentell – zu einer wahren Revolution in der Gemeinschaft. Der theoretische Durchbruch war die Vapnik–Chervonenkis (VC)-Theorie12. Die VC-Theorie bewies, dass bei Betrachtung spezifischer Modelltypen der tatsächliche Fehler oberhalb durch das grob der Summe aus dem empirischen Fehler plus dem strukturellen Risiko entsprach, einer intrinsischen Eigenschaft des Modells selbst. In diesem Zusammenhang ist „tatsächlicher Fehler“ der Fehler, der bei den Daten auftritt, die man nicht hat, während der „empirische Fehler“ der Fehler bei den Daten ist, die man hat. Durch Minimierung der Summe aus dem empirischen Fehler und dem strukturellen Risiko konnte der tatsächliche Fehler eingeschränkt werden. Dies stellte sowohl ein erstaunliches Ergebnis als auch, man könnte sagen, den größten Schritt in Richtung Generalisierung seit der Identifizierung des Overfitting-Problems dar.
Auf der experimentellen Seite wurden Modelle, die später als Support Vector Machines (SVMs) bekannt wurden, fast als eine Lehrbuchableitung dessen eingeführt, was die VC-Theorie über das Lernen festgestellt hatte. Diese SVMs wurden zu den ersten weit verbreiteten, erfolgreichen Modellen, die es ermöglichten, mit Datensätzen zu arbeiten, bei denen die Anzahl der Dimensionen die Anzahl der Beobachtungen überstieg.
Durch das Einrahmen des tatsächlichen Fehlers, ein wirklich überraschendes theoretisches Ergebnis, hatte die VC-Theorie die Dimensionsbarriere durchbrochen – etwas, das fast ein Jahrhundert lang problematisch geblieben war. Sie ebnete auch den Weg für Modelle, die hochdimensionale Daten nutzen können. Doch schon bald wurden die SVMs selbst durch alternative Modelle verdrängt, vor allem durch Ensemble-Methoden (Random Forests13 und Gradient Boosting), die sich in den frühen 2000er-Jahren als überlegene Alternativen14 erwiesen – sowohl in Bezug auf die Generalisierung als auch hinsichtlich der Rechenanforderungen. Wie die SVMs, die sie ersetzten, profiterten auch die Ensemble-Methoden von theoretischen Garantien hinsichtlich ihrer Fähigkeit, Overfitting zu vermeiden. All diese Methoden teilen die Eigenschaft, nichtparametrisch zu sein. Die Dimensionsbarriere wurde durch die Einführung von Modellen durchbrochen, die nicht für jede Dimension einen oder mehrere Parameter einführen mussten – und gingen so einen bekannten Weg, um Overfitting-Probleme zu umgehen.
Kehren wir zurück zum zuvor erwähnten Problem der unplanmäßigen Reparaturen: Anders als die klassischen statistischen Modelle – wie die lineare Regression, die an der Dimensionsbarriere scheitert – schaffen es Ensemble-Methoden, den großen Datensatz mit seinen 10.000 Dimensionen zu nutzen, obwohl es nur 100 Beobachtungen gibt. Darüber hinaus funktionieren Ensemble-Methoden mehr oder weniger direkt out of the box. Operativ war dies eine bemerkenswerte Entwicklung, da es die Notwendigkeit beseitigte, Modelle penibel zu gestalten, indem man das exakt richtige Set an Eingabedimensionen auswählte.
Der Einfluss auf die breitere Gemeinschaft – sowohl innerhalb als auch außerhalb der Wissenschaft – war enorm. Der Großteil der Forschungsanstrengungen in den frühen 2000er-Jahren widmete sich der Erforschung dieser nichtparametrischen, „theoriegestützten“ Ansätze. Dennoch verdampften die Erfolge im Laufe der Jahre recht schnell. Tatsächlich bleiben auch rund zwanzig Jahre später die besten Modelle der sogenannten statistischen Lern-Perspektive dieselben – sie profitieren lediglich von leistungsfähigeren Implementierungen15.
Das tiefe Double-Descent
Bis 2010 galt die konventionelle Weisheit, dass zur Vermeidung von Overfitting-Problemen die Anzahl der Parameter wesentlich kleiner als die Anzahl der Beobachtungen bleiben muss. Tatsächlich repräsentiert jeder Parameter implizit einen Freiheitsgrad, sodass so viele Parameter wie Beobachtungen ein Rezept für Overfitting sind16. Ensemble-Methoden umgingen das Problem von vornherein, indem sie nichtparametrisch waren. Dennoch stellte sich diese grundlegende Erkenntnis als falsch heraus – und zwar spektakulär.
Was später als der Deep Learning-Ansatz bekannt wurde, überraschte nahezu die gesamte Gemeinschaft mit hyperparametrischen Modellen. Diese Modelle überfitten nicht, enthalten jedoch vielfach mehr Parameter als Beobachtungen.
Die Entstehung des Deep Learning ist komplex und lässt sich auf die frühesten Versuche zurückführen, die Prozesse des Gehirns zu modellieren – namentlich neuronale Netzwerke. Eine detaillierte Darstellung dieser Entstehung sprengt den Rahmen der vorliegenden Diskussion, jedoch ist bemerkenswert, dass die Deep Learning-Revolution Anfang der 2010er-Jahre begann, gerade als das Feld die Metapher des neuronalen Netzwerks zugunsten mechanischer Sympathie aufgab. Die Deep Learning-Implementierungen ersetzten die bisherigen Modelle durch viel einfachere Varianten. Diese neueren Modelle nutzten alternative Computing-Hardware, insbesondere GPUs (Graphics Processing Units), die sich, etwas zufällig, als gut geeignet für die linearen Algebraoperationen erwiesen, die Deep Learning-Modelle charakterisieren17.
Es dauerte fast weitere fünf Jahre, bis Deep Learning allgemein als Durchbruch anerkannt wurde. Ein erheblicher Teil der Zurückhaltung kam aus dem Lager des statistischen Lernens – zufälligerweise jener Teil der Gemeinschaft, der vor zwei Jahrzehnten erfolgreich die Dimensionsbarriere durchbrochen hatte. Während die Erklärungen für diese Zurückhaltung variieren, trug der scheinbare Widerspruch zwischen der konventionellen Overfitting-Weisheit und den Behauptungen des Deep Learning sicherlich zu einem bemerkenswerten Maß an anfänglichem Skeptizismus gegenüber dieser neueren Modellklasse bei.
Der Widerspruch blieb weitgehend ungelöst, bis 2019 der tiefe Double Descent identifiziert wurde18 – ein Phänomen, das das Verhalten bestimmter Modellklassen charakterisiert. Bei solchen Modellen verschlechtert eine Erhöhung der Anzahl der Parameter zunächst den Testfehler (aufgrund von Overfitting), bis die Anzahl der Parameter so groß wird, dass der Trend umgekehrt und der Testfehler wieder verbessert wird. Der „zweite Abstieg“ (des Testfehlers) war kein Verhalten, das aus der Bias-Tradeoff-Perspektive vorhergesagt wurde.
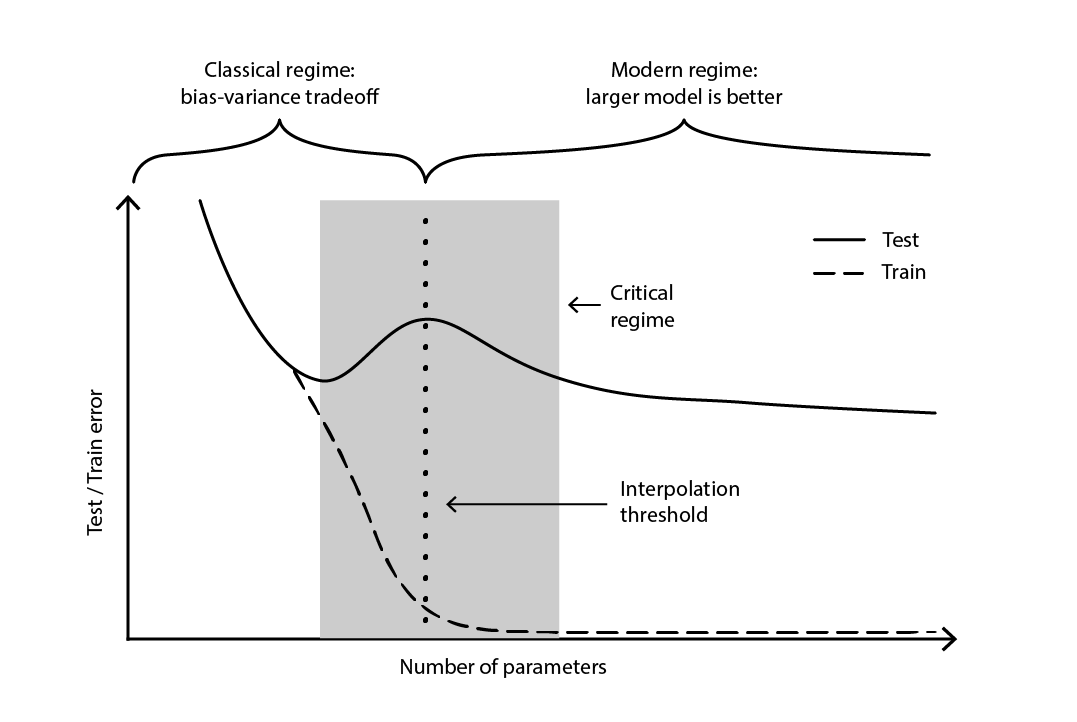
Abbildung 4. Ein tiefer Double Descent.
Abbildung 4 veranschaulicht die beiden aufeinanderfolgenden Regime, die oben beschrieben wurden. Das erste Regime ist der klassische Bias-Variance-Tradeoff, der scheinbar mit einer „optimalen“ Anzahl von Parametern einhergeht. Doch dieses Minimum erweist sich als lokales Minimum. Es gibt ein zweites Regime, das zu beobachten ist, wenn man die Anzahl der Parameter weiter erhöht, und das eine asymptotische Konvergenz zu einem tatsächlich optimalen Testfehler des Modells zeigt.
Der tiefe Double Descent vereinte nicht nur die statistische und die Deep Learning-Perspektive, sondern zeigte auch, dass Generalisierung immer noch relativ wenig verstanden wird. Er bewies, dass die weit verbreiteten Theorien – bis in die späten 2010er-Jahre alltäglich – eine verzerrte Sicht auf die Generalisierung präsentierten. Dennoch liefert der tiefe Double Descent noch keinen Rahmen – oder etwas Äquivalentes –, der die Generalisierungskraft (oder das Fehlen derselben) von Modellen basierend auf ihrer Struktur vorhersagen würde. Bis heute bleibt der Ansatz konsequent empirisch.
Die supply chain-Dornen
Wie ausführlich behandelt, ist Generalisierung äußerst herausfordernd, und supply chains schaffen es, ihre eigenen Macken einzubringen, was die Situation weiter verschärft. Erstens bleiben die Daten, nach denen supply chain-Experten suchen, möglicherweise für immer unzugänglich – nicht nur teilweise ungesehen, sondern völlig unbeobachtbar. Zweitens kann der Akt der Vorhersage die Zukunft verändern sowie die Gültigkeit der Vorhersage, da Entscheidungen auf genau diesen Vorhersagen basieren. Daher sollte man bei der Herangehensweise an die Generalisierung im Kontext der supply chain einen zweigleisigen Ansatz verfolgen – einerseits die statistische Solidität des Modells und andererseits das hochrangige Denkvermögen, das das Modell untermauert.
Außerdem sind die verfügbaren Daten nicht immer die gewünschten Daten. Betrachten Sie einen Hersteller, der die Nachfrage prognostizieren möchte, um die zu produzierenden Mengen zu bestimmen. Es gibt keine historischen „Nachfragedaten“ im eigentlichen Sinne. Stattdessen stellen die historischen Verkaufsdaten den besten verfügbaren Proxy für den Hersteller dar, um die historische Nachfrage abzubilden. Allerdings werden die historischen Verkäufe durch vergangene stock-outs verzerrt. Null Verkäufe, hervorgerufen durch stock-outs, sollten nicht mit null Nachfrage verwechselt werden. Während ein Modell entwickelt werden kann, um diese Verkaufshistorie in eine Art Nachfragemuster umzuwandeln, ist der Generalisierungsfehler dieses Modells per Design schwer fassbar, da weder die Vergangenheit noch die Zukunft diese Daten enthält. Kurz gesagt ist „Nachfrage“ ein notwendiges, aber immaterielles Konstrukt.
Im Jargon des maschinellen Lernens ist die Modellierung der Nachfrage ein Problem des unüberwachten Lernens, bei dem der Output des Modells niemals direkt beobachtet wird. Dieser unüberwachte Aspekt unterläuft die meisten Lernalgorithmen und auch die meisten Techniken zur Modellvalidierung – zumindest in ihrer „naiven“ Form. Darüber hinaus untergräbt er auch den eigentlichen Gedanken eines prediction competition, wobei hier ein einfacher zweistufiger Prozess gemeint ist, bei dem ein ursprünglicher Datensatz in einen öffentlichen (Trainings-) und einen privaten (Validierungs-)Teil aufgeteilt wird. Die Validierung selbst wird zwangsläufig zu einer Modellierungsübung.
Einfach ausgedrückt wird die vom Hersteller erstellte Vorhersage – auf die eine oder andere Weise – die Zukunft des Herstellers prägen. Eine hohe prognostizierte Nachfrage bedeutet, dass der Hersteller die Produktion hochfahren wird. Wenn das Unternehmen gut geführt wird, werden economies of scale wahrscheinlich im Produktionsprozess erreicht, was die Produktionskosten senkt. Im Gegenzug wird der Hersteller voraussichtlich diese neu gewonnenen wirtschaftlichen Vorteile nutzen, um die Preise zu senken und sich so einen Wettbewerbsvorteil gegenüber Konkurrenten zu verschaffen. Der Markt, der die günstigste Option sucht, könnte diesen Hersteller rasch als seinen wettbewerbsfähigsten Anbieter übernehmen und dadurch eine Nachfragewelle auslösen, die weit über die anfängliche Prognose hinausgeht.
Dieses Phänomen ist als self-fulfilling prophecy bekannt – eine Vorhersage, die dadurch zur Wahrheit wird, dass der Glaube der Beteiligten an die Vorhersage selbst sie beeinflusst. Eine unorthodoxe, aber nicht völlig unvernünftige Perspektive würde supply chains als riesige, sich selbst erfüllende Rube-Goldberg-Apparate charakterisieren. Auf methodischer Ebene verkompliziert diese Verflechtung von Beobachter und Beobachtung die Situation zusätzlich, da die Generalisierung mit der Erfassung der zugrunde liegenden strategischen Absicht verbunden wird, die den Entwicklungen in der supply chain zugrunde liegt.
An diesem Punkt mag die Generalisierungsherausforderung, wie sie sich in der supply chain darstellt, unüberwindbar erscheinen. Tabellenkalkulationen, die in supply chains allgegenwärtig sind, deuten sicherlich darauf hin, dass dies die standardmäßige, wenn auch implizite, Haltung der meisten Unternehmen ist. Eine Tabellenkalkulation ist jedoch in erster Linie ein Werkzeug, um die Lösung des Problems an ein ad-hoc menschliches Urteil zu delegieren, anstatt eine systematische Methode anzuwenden.
Auch wenn das Zurückgreifen auf menschliches Urteil an sich stets die falsche Antwort ist, bietet es keine befriedigende Lösung des Problems. Das Vorhandensein von stock-outs bedeutet nicht, dass bei der Nachfrage alles möglich ist. Sicherlich, wenn der Hersteller in den letzten drei Jahren durchschnittliche service levels von über 90% beibehalten hat, wäre es höchst unwahrscheinlich, dass die (beobachtete) Nachfrage zehnmal so hoch wie die Verkäufe sein könnte. Daher ist es vernünftig zu erwarten, dass eine systematische Methode entwickelt werden kann, um mit solchen Verzerrungen umzugehen. Ebenso kann die self-fulfilling prophecy modelliert werden, insbesondere durch das Konzept der Policy, wie es in der Regelungstechnik verstanden wird.
Wenn man also eine reale supply chain betrachtet, erfordert die Generalisierung einen zweigleisigen Ansatz. Zunächst muss das Modell statistisch fundiert sein, soweit es die breit gefächerte „learning“-Wissenschaft zulässt. Dies umfasst nicht nur theoretische Perspektiven wie die klassische Statistik und das statistische Lernen, sondern auch empirische Bestrebungen wie maschinelles Lernen und prediction competitions. Die Rückkehr zur Statistik des 19. Jahrhunderts ist kein vernünftiges Konzept für eine 21. Jahrhundert supply chain practice.
Zweitens muss das Modell durch gehobene Argumentation unterstützt werden. Mit anderen Worten, für jede Komponente des Modells und jeden Schritt des Modellierungsprozesses sollte es eine Begründung geben, die aus der supply chain Perspektive Sinn macht. Ohne diese Zutat ist operatives Chaos19 nahezu garantiert, in der Regel ausgelöst durch eine Entwicklung der supply chain selbst, ihres Betriebsökosystems oder ihrer zugrunde liegenden anwendungsbezogenen Landschaft. Tatsächlich besteht der ganze Sinn der gehobenen Argumentation nicht darin, ein Modell einmalig funktionieren zu lassen, sondern es nachhaltig über mehrere Jahre in einem sich ständig verändernden Umfeld zum Laufen zu bringen. Diese Argumentation ist die nicht ganz geheime Zutat, die dabei hilft zu entscheiden, dass es an der Zeit ist, das Modell zu überarbeiten, wenn dessen Design, was auch immer es sein mag, nicht mehr mit der Realität und/oder den Geschäftszielen in Einklang steht.
Aus der Ferne könnte dieser Vorschlag anfällig erscheinen für die frühere an Tabellenkalkulationen gerichtete Kritik – jene, die dagegen spricht, mühsame Arbeit an eine schwer fassbare „menschliche Urteilskraft“ abzugeben. Obwohl dieser Vorschlag die Bewertung des Modells weiterhin der menschlichen Urteilskraft überlässt, soll die Ausführung des Modells vollständig automatisiert erfolgen. Folglich sollen die täglichen Abläufe vollständig automatisiert sein, auch wenn die laufenden technischen Bemühungen, die numerischen Rezepte weiter zu verbessern, dies nicht sind.
Anmerkungen
-
Es gibt eine wichtige algorithmische Technik namens “memoization”, die ein Ergebnis, das neu berechnet werden könnte, durch sein vorab berechnetes Ergebnis ersetzt und somit mehr Speicher gegen weniger Rechenleistung tauscht. Diese Technik ist jedoch für die vorliegende Diskussion nicht relevant. ↩︎
-
Warum die meisten veröffentlichten Forschungsergebnisse falsch sind, John P. A. Ioannidis, August 2005 ↩︎
-
Aus der Perspektive der Zeitreihenprognose wird der Begriff der Generalisierung durch das Konzept der “Genauigkeit” betrachtet. Genauigkeit kann als Sonderfall der “Generalisierung” angesehen werden, wenn es um Zeitreihen geht. ↩︎
-
Makridakis, S.; Andersen, A.; Carbone, R.; Fildes, R.; Hibon, M.; Lewandowski, R.; Newton, J.; Parzen, E.; Winkler, R. (April 1982). “Die Genauigkeit von Extrapolationstechniken (Zeitreihen): Ergebnisse eines Prognosewettbewerbs”. Journal of Forecasting. 1 (2): 111–153. doi:10.1002/for.3980010202. ↩︎
-
Kaggle in Numbers, Carl McBride Ellis, abgerufen am 8. Februar 2023, ↩︎
-
Der 1935 entnommene Ausschnitt “Perhaps we are old fashioned but to us a six-variate analysis based on thirteen observations seems rather like overfitting” aus “The Quarterly Review of Biology” (Sep, 1935, Band 10, Nummer 3, S. 341 – 377) scheint darauf hinzuweisen, dass das statistische Konzept der Überanpassung zu dieser Zeit bereits etabliert war. ↩︎
-
Grenander, Ulf. Zur empirischen Spektralanalyse stochastischer Prozesse. Ark. Mat., 1(6):503–531, 08 1952. ↩︎
-
Whittle, P. Tests of Fit in Time Series, Bd. 39, Nr. 3/4 (Dez., 1952), S. 309-318 (10 Seiten), Oxford University Press ↩︎
-
Everitt B.S., Skrondal A. (2010), Cambridge Dictionary of Statistics, Cambridge University Press. ↩︎
-
Die asymptotischen Vorteile der Verwendung höherer k-Werte beim k-fachen Kreuzvalidierungsverfahren lassen sich aus dem zentralen Grenzwertsatz ableiten. Diese Erkenntnis legt nahe, dass wir uns durch Erhöhung von k etwa 1 / sqrt(k) dem vollständigen Verbesserungspotenzial nähern können, das der k-fache ursprünglich bot. ↩︎
-
Support-Vektor-Netzwerke, Corinna Cortes, Vladimir Vapnik, Machine Learning, Band 20, S. 273–297 (1995) ↩︎
-
Die Vapnik-Chervonenkis-(VC)-Theorie war nicht der einzige Kandidat, um zu formalisieren, was “Lernen” bedeutet. Valiants PAC-(probably approximately correct)-Rahmenwerk von 1984 ebnete den Weg für formale Lernansätze. Allerdings fehlte dem PAC-Rahmenwerk die enorme Durchsetzungskraft und die operationellen Erfolge, die die VC-Theorie um die Jahrtausendwende genoss. ↩︎
-
Random Forests, Leo Breiman, Machine Learning, Band 45, S. 5–32 (2001) ↩︎
-
Eine der bedauerlichen Konsequenzen, dass Support Vector Machines (SVMs), die stark von einer mathematischen Theorie inspiriert sind, wenig “mechanisches Verständnis” für moderne Computerhardware haben, ist, dass die relative Unzulänglichkeit von SVMs zur Verarbeitung großer Datensätze – einschließlich Millionen von Beobachtungen oder mehr – im Vergleich zu Alternativen den Niedergang dieser Methoden einleitete. ↩︎
-
XGBoost und LightGBM sind zwei Open-Source-Implementierungen der Ensemble-Methoden, die innerhalb der Machine-Learning-Community nach wie vor sehr beliebt sind. ↩︎
-
Der Kürze halber wird hier ein gewisses Maß an Vereinfachung vorgenommen. Es gibt ein ganzes Forschungsfeld, das sich der “Regularisierung” statistischer Modelle widmet. Bei Vorliegen von Regularisierungszwängen kann die Anzahl der Parameter – selbst bei einem klassischen Modell wie der linearen Regression – die Anzahl der Beobachtungen bedenkenlos überschreiten. In Anwesenheit von Regularisierung repräsentiert jedoch kein Parameterwert mehr vollständig einen Freiheitsgrad, sondern nur einen Bruchteil davon. Daher wäre es korrekter, von der Anzahl der Freiheitsgrade zu sprechen, anstatt von der Anzahl der Parameter. Da diese peripheren Betrachtungen die hier dargestellten Ansichten nicht grundlegend verändern, genügt die vereinfachte Version. ↩︎
-
Tatsächlich ist die Kausalität umgekehrt. Pioniere des Deep Learning schafften es, ihre ursprünglichen Modelle – neuronale Netzwerke – in einfachere Modelle umzuwandeln, die fast ausschließlich auf linearer Algebra basierten. Der Sinn dieser Umgestaltung bestand genau darin, diese neueren Modelle auf Computerhardware auszuführen, die Vielseitigkeit gegen rohe Leistung eintauscht, namentlich GPUs. ↩︎
-
Deep Double Descent: Where Bigger Models and More Data Hurt, Preetum Nakkiran, Gal Kaplun, Yamini Bansal, Tristan Yang, Boaz Barak, Ilya Sutskever, Dezember 2019 ↩︎
-
Der Großteil der Data-Science-Initiativen in der supply chain scheitert. Meine beiläufigen Beobachtungen deuten darauf hin, dass die Unkenntnis dessen, was die supply chain antreibt, bei Data Scientists die Hauptursache für die meisten dieser Fehlschläge ist. Obwohl es unglaublich verlockend ist – für einen neu ausgebildeten Data Scientist – das neueste und glänzendste Open-Source-Machine-Learning-Paket zu nutzen, sind nicht alle Modellierungstechniken gleichermaßen dafür geeignet, die gehobene Argumentation zu unterstützen. Tatsächlich sind die meisten der “Mainstream”-Techniken, wenn es um den Whiteboxing-Prozess geht, schlichtweg schrecklich. ↩︎