Probabilistische Prognose (supply chain)

Eine Prognose wird als probabilistisch statt deterministisch bezeichnet, wenn sie ein Bündel von Wahrscheinlichkeiten enthält, die allen möglichen zukünftigen Ergebnissen zugeordnet sind, anstatt ein einzelnes Ergebnis als „die“ Prognose festzulegen. Probabilistische Prognosen sind wichtig, wenn Ungewissheit irreduzibel ist, was fast immer der Fall ist, wenn es um komplexe Systeme geht. Für supply chain sind probabilistische Prognosen unerlässlich, um robuste Entscheidungen angesichts unsicherer zukünftiger Bedingungen zu treffen. Insbesondere werden Nachfrage und Lieferzeit, zwei zentrale Aspekte der supply chain Analyse, beide am besten durch probabilistische Prognosen adressiert. Die probabilistische Perspektive eignet sich von Natur aus zur wirtschaftlichen Priorisierung von Entscheidungen, basierend auf ihren erwarteten, aber unsicheren Renditen. Eine Vielzahl statistischer Modelle liefert probabilistische Prognosen. Einige sind ihren deterministischen Gegenstücken strukturell ähnlich, während andere ganz anders sind. Die Bewertung der Genauigkeit einer probabilistischen Prognose erfordert spezielle Metriken, die sich von denen der deterministischen Prognosen unterscheiden. Die Nutzung probabilistischer Prognosen erfordert spezialisierte Werkzeuge, die von ihren deterministischen Pendants abweichen.

Deterministische vs. Probabilistische Prognosen

Die Optimierung von supply chain beruht auf der richtigen Vorwegnahme zukünftiger Ereignisse. Numerisch werden diese Ereignisse durch Prognosen vorausgesehen, die eine Vielzahl von numerischen Methoden umfassen, mit denen diese zukünftigen Ereignisse quantifiziert werden. Seit den 1970er Jahren ist die am weitesten verbreitete Form der Prognose die deterministische Zeitreihen-Prognose: Eine über die Zeit gemessene Größe – zum Beispiel die Nachfrage in Stückzahlen für ein Produkt – wird in die Zukunft projiziert. Der vergangene Abschnitt der Zeitreihe stellt die historischen Daten dar, der zukünftige Abschnitt die Prognose.

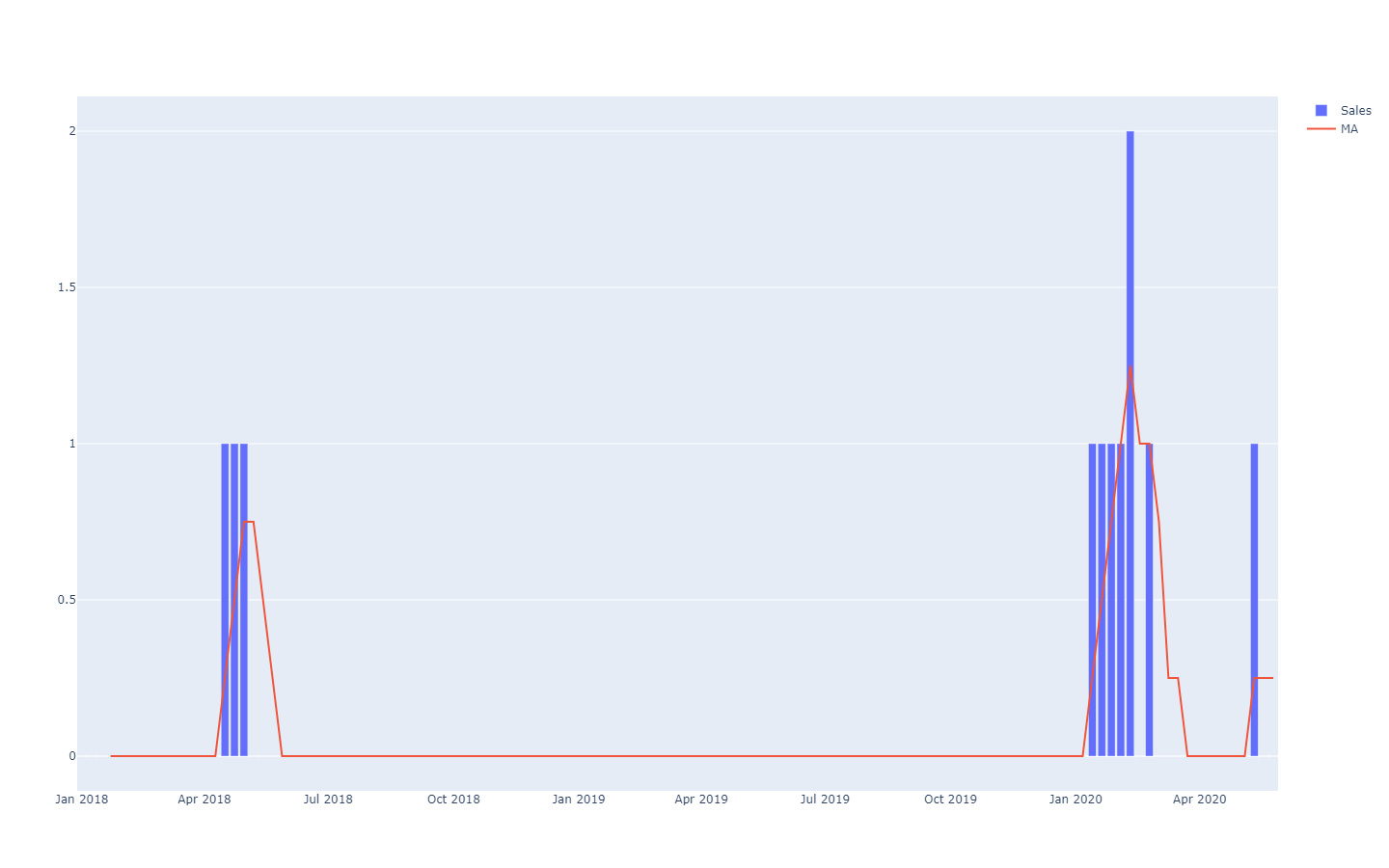
Diese Zeitreihen-Prognosen werden als deterministisch bezeichnet, weil sie für jeden zukünftigen Zeitpunkt einen einzelnen Wert liefern, der dem zukünftigen Ergebnis so genau wie möglich entsprechen soll. Zwar liefert die Prognose einen Einzelwert, doch man geht allgemein davon aus, dass sie kaum perfekt richtig sein kann. Zukünftige Ergebnisse werden von der Prognose abweichen. Die Übereinstimmung der deterministischen Prognose mit ihren zukünftigen Ergebnissen wird quantitativ anhand von Genauigkeitsmetriken bewertet, wie zum Beispiel dem mittleren quadratischen Fehler (MSE).

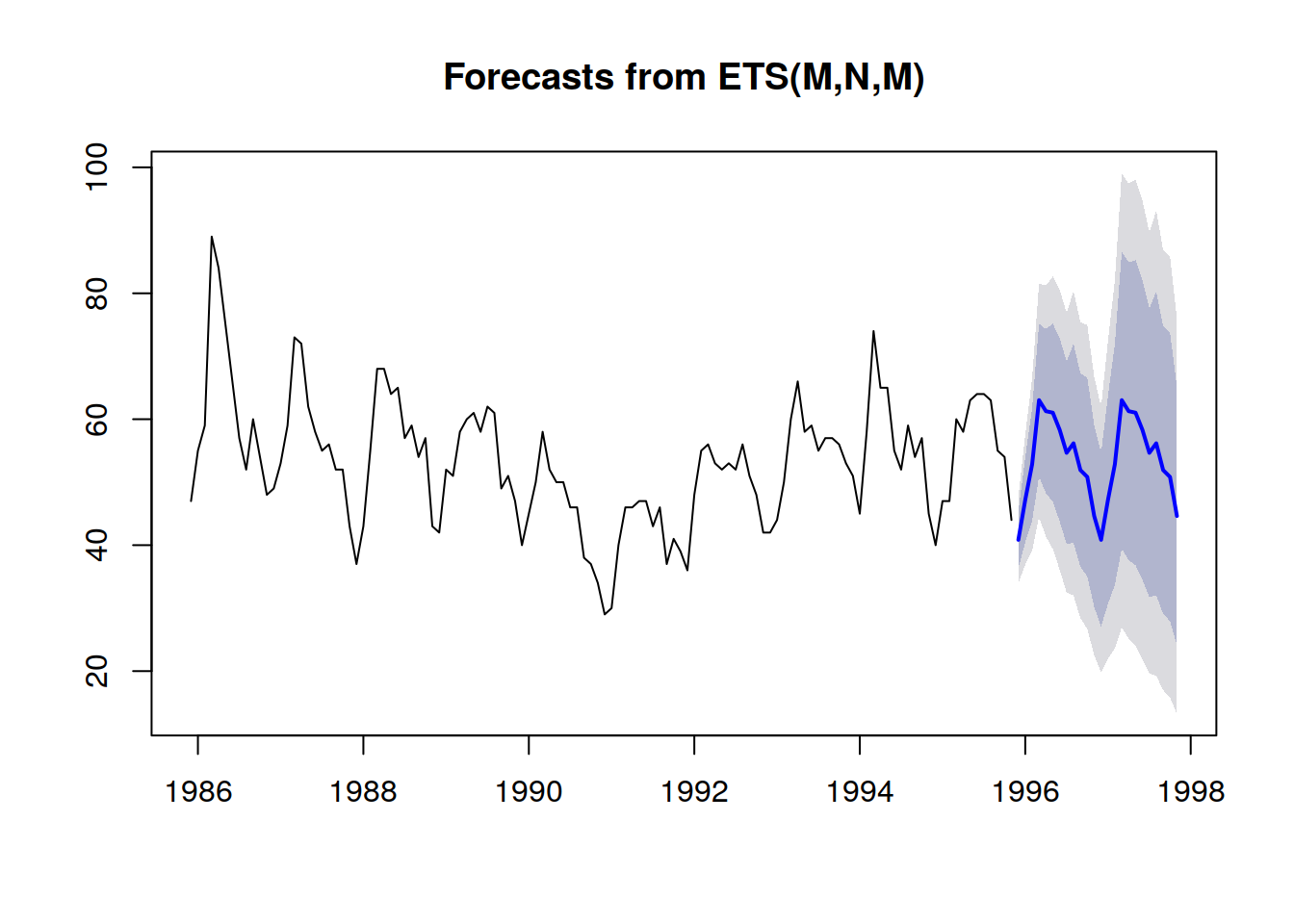
Probabilistische Prognosen verfolgen eine andere Perspektive bei der Vorwegnahme zukünftiger Ergebnisse. Anstatt einen einzelnen Wert als das „beste“ Ergebnis zu liefern, besteht die probabilistische Prognose darin, jedem möglichen Ergebnis eine Wahrscheinlichkeit zuzuordnen. Mit anderen Worten, alle zukünftigen Ereignisse bleiben möglich, sie sind nur nicht gleichermaßen wahrscheinlich. Untenstehend ist die Visualisierung einer probabilistischen Zeitreihen-Prognose zu sehen, die den „Shotgun-Effekt“ zeigt, der typischerweise in den meisten realen Situationen beobachtet wird. Wir werden diese Visualisierung im Folgenden noch detaillierter betrachten.

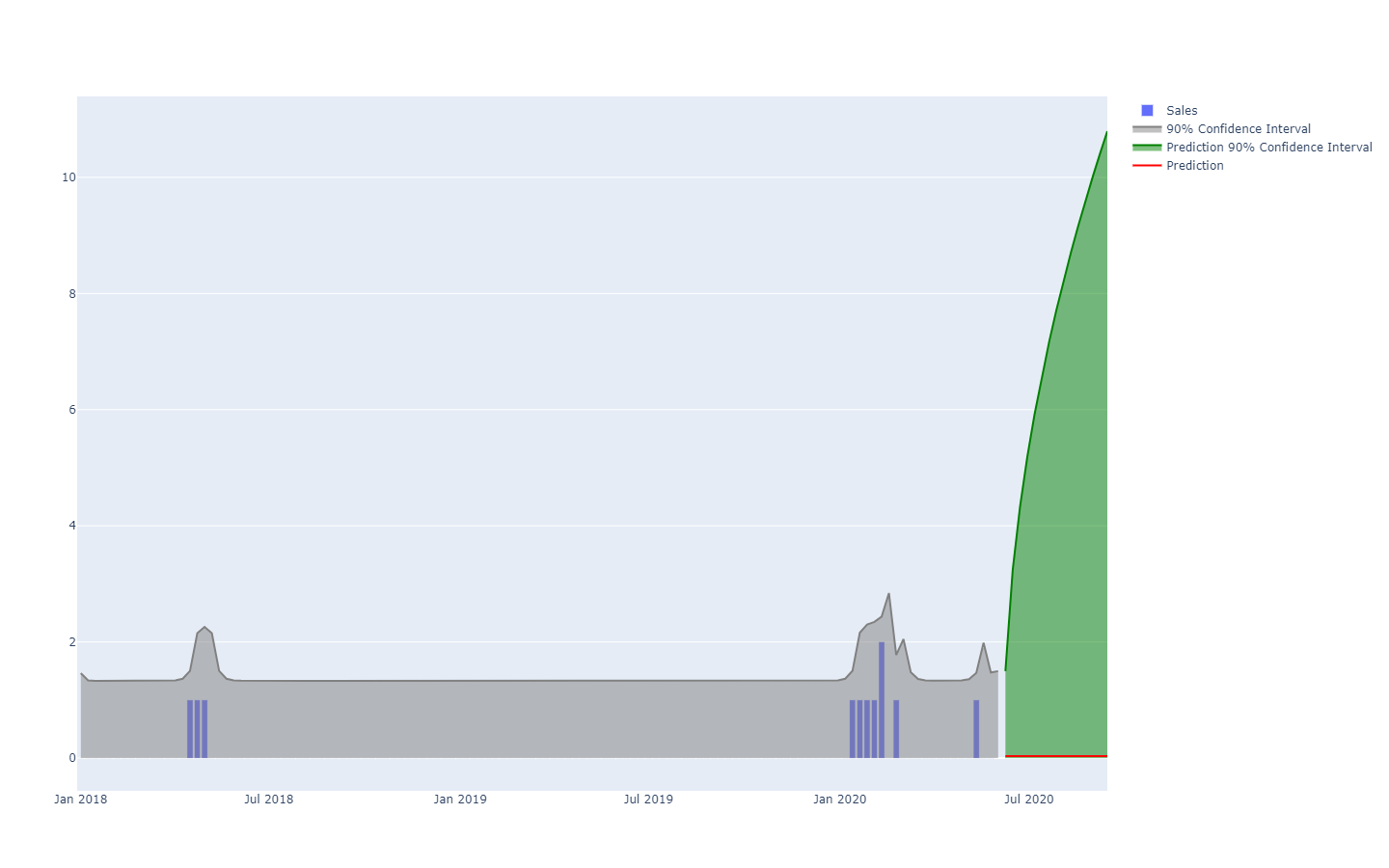
Zeitreihen, eine über die Zeit gemessene Größe, sind vermutlich das bekannteste und am häufigsten verwendete Datenmodell. Dieses Datenmodell kann sowohl deterministisch als auch probabilistisch prognostiziert werden. Allerdings gibt es viele alternative, typischerweise umfangreichere Datenmodelle, die ebenfalls Prognosen beider Art ermöglichen. Zum Beispiel möchte ein Unternehmen, das Düsentriebwerke repariert, möglicherweise die genaue Liste der Ersatzteile antizipieren, die für einen bevorstehenden Wartungseinsatz benötigt werden. Diese Antizipation kann in Form einer Prognose erfolgen, jedoch wird es keine Zeitreihen-Prognose sein. Die deterministische Prognose, die mit diesem Einsatz verbunden ist, ist die exakte Liste der Teile und ihrer Mengen. Umgekehrt ist die probabilistische Prognose die Wahrscheinlichkeit, dass jede Kombination von Teilen (einschließlich Mengen) genau diejenige ist, die für die Durchführung der Reparaturen benötigt wird.

Außerdem, obwohl der Begriff „Prognose“ eine Art Vorhersage betont, kann die Idee auf jede Art von statistisch abgeleiteter Aussage über ein System verallgemeinert werden, einschließlich seiner vergangenen (aber unbekannten) Eigenschaften. Die Praxis der statistischen Prognose entstand im 20. Jahrhundert, vor dem Aufkommen der moderneren statistical learning-Perspektive, die alle datengesteuerten Extrapolationen umfasst, die durchgeführt werden können, unabhängig von irgendeiner zeitlichen Dimension. Zur besseren Verständlichkeit werden wir im Folgenden weiterhin den Begriff „Prognose“ verwenden, selbst wenn der zeitliche Aspekt immer Vergangenheit mit Bekanntem und Zukunft mit Unbekanntem gleichsetzt. Zum Beispiel möchte ein Unternehmen möglicherweise den Umsatz schätzen, der für ein Produkt in einem Geschäft erzielt worden wäre, wenn das Produkt an diesem Tag nicht fehlbestand gewesen wäre. Die Schätzung ist nützlich, um das Ausmaß des Problems in Bezug auf die Servicequalität zu quantifizieren. Da das Ereignis jedoch in der Vergangenheit liegt, wird die „tatsächliche“ Verkaufszahl niemals beobachtet werden. Nichtsdestotrotz, sofern sie noch nicht trivial beobachtet wurde, ist die statistische Schätzung der vergangenen Nachfrage ein Problem, das der Schätzung der zukünftigen Nachfrage sehr nahekommt.

Probabilistische Prognosen sind informationsmäßig umfangreicher als ihre deterministischen Gegenstücke. Während die deterministische Prognose eine „beste Schätzung“ des zukünftigen Ergebnisses liefert, sagt sie nichts über die Alternativen aus. Tatsächlich ist es immer möglich, eine probabilistische Prognose in ihr deterministisches Gegenstück umzuwandeln, indem man den Mittelwert, den Median, den Modus usw. der Wahrscheinlichkeitsverteilung heranzieht. Umgekehrt gilt dies jedoch nicht: Es ist nicht möglich, eine probabilistische Prognose aus einer deterministischen zu rekonstruieren.

Dennoch, obwohl probabilistische Prognosen statistisch überlegen sind im Vergleich zu deterministischen Prognosen, werden sie in supply chain nur selten verwendet. Ihre Beliebtheit hat jedoch im letzten Jahrzehnt stetig zugenommen. Historisch gesehen entstanden probabilistische Prognosen später, da sie wesentlich mehr Rechenressourcen erfordern. Der Einsatz probabilistischer Prognosen für supply chain Zwecke erfordert zudem spezialisierte Softwarewerkzeuge, die oft nicht verfügbar sind.

Supply chain Anwendungsfälle

Die Optimierung einer supply chain besteht darin, die „richtige“ Entscheidung – im gegenwärtigen Moment – zu treffen, die eine zukünftige Situation, die nur unvollständig geschätzt wurde, am gewinnträchtigsten adressiert. Allerdings ist die mit zukünftigen Ereignissen verbundene Unsicherheit weitgehend irreduzibel. Daher muss die Entscheidung robust sein, falls die Vorwegnahme des zukünftigen Ereignisses – also der Prognose – unvollkommen ist. Dies wurde seit Mitte des 20. Jahrhunderts minimal durch die Sicherheitsbestandsanalyse gemacht. Wie wir aber unten sehen werden, gibt es neben historischem Interesse keinen Grund mehr, Sicherheitsbestände gegenüber „nativen“ probabilistischen numerischen Rezepten zu bevorzugen.

Die Perspektive der probabilistischen Prognose nimmt eine radikale Haltung gegenüber der Unsicherheit ein: Dieser Ansatz versucht, die Unsicherheit in größtmöglichem Maße zu quantifizieren. In supply chain konzentrieren sich die Kosten tendenziell auf die statistischen Extreme: Es ist die unerwartet hohe Nachfrage, die einen Engpass verursacht, es ist die unerwartet niedrige Nachfrage, die zu einer Abschreibung des Inventars führt. Dazwischen rotiert das Inventar ganz normal. Probabilistische Prognosen sind – grob gesagt – ein Versuch, diese seltenen, aber kostenintensiven Situationen zu managen, die in modern supply chains allgegenwärtig sind. Probabilistische Prognosen können und sollten als wesentlicher Bestandteil jeder Risikomanagementpraxis innerhalb der supply chain gesehen werden.

Viele Aspekte von supply chain eignen sich besonders für probabilistische Prognosen, wie zum Beispiel:

• Nachfrage: Bekleidung, Accessoires, Ersatzteile sowie viele andere Produkttypen sind in der Regel mit unregelmäßiger und/oder intermittierender Nachfrage verbunden. Produkteinführungen können Erfolg oder Misserfolg sein. Promotions von Wettbewerbern können vorübergehend und unregelmäßig große Teile der Marktanteile kannibalisieren.
• Lieferzeit: Importe aus Übersee können an jeder Stelle der chain (Produktion, Transport, Zoll, Empfang etc.) eine ganze Reihe von Verzögerungen mit sich bringen. Auch lokale Lieferanten können vereinzelt lange Lieferzeiten haben, wenn sie ein Lagerengpassproblem haben. Lieferzeiten tendieren zu dickschwänzigen Verteilungen.
• Ertrag (frische Lebensmittel): Die Menge und Qualität der Produktion vieler Frischwaren hängen von Bedingungen ab, wie zum Beispiel dem Wetter, die außerhalb der Kontrolle des Unternehmens liegen. Die probabilistische Prognose quantifiziert diese Faktoren für die gesamte Saison und bietet die Möglichkeit, über den Gültigkeitsbereich klassischer Wettervorhersagen hinauszugehen.
• Retouren (E-Commerce): Wenn ein Kunde dasselbe Produkt in drei verschiedenen Größen bestellt, ist es sehr wahrscheinlich, dass zwei dieser Größen zurückgesendet werden. Allgemeiner, auch wenn es starke regionale Unterschiede gibt, neigen Kunden dazu, günstige Rückgabebedingungen zu nutzen, wenn diese vorhanden sind. Die Wahrscheinlichkeit von Retouren für jede Bestellung sollte bewertet werden.
• Ausschuss (Luftfahrt): Reparierbare Flugzeugteile – häufig als Rotables bezeichnet – können manchmal nicht repariert werden. In diesem Fall wird das Teil verschrottet, da es nicht wieder an einem Flugzeug montiert werden kann. Obwohl es in der Regel nicht möglich ist, im Voraus zu wissen, ob ein Teil seine Reparatur übersteht oder nicht, sollten die Chancen, dass das Teil verschrottet wird, abgeschätzt werden.
• Bestände (B2C Einzelhandel): Kunden können Waren in einem Geschäft verschieben, beschädigen oder sogar stehlen. Daher ist der elektronische Bestandswert nur eine Annäherung an die tatsächliche Verfügbarkeit im Regal, wie sie von den Kunden wahrgenommen wird. Der vom Kunden wahrgenommene Bestandswert sollte durch eine probabilistische Prognose geschätzt werden.
• …

Diese kurze Liste zeigt, dass die Blickwinkel, die für eine probabilistische Prognose in Frage kommen, die traditionellen, ausschließlich auf Nachfrage basierenden Ansätze bei weitem übersteigen. Die bestens konzipierte Optimierung einer supply chain erfordert, alle relevanten Quellen der Unsicherheit zu berücksichtigen. Auch wenn es manchmal möglich ist, die Unsicherheit zu reduzieren – wie es bei der schlanken Produktion betont wird – sind in der Regel wirtschaftliche Trade-offs involviert, und infolgedessen bleibt ein gewisses Maß an Unsicherheit irreduzibel.

Prognosen sind jedoch lediglich fundierte Vermutungen über die Zukunft. Obwohl probabilistische Prognosen als bemerkenswert detaillierte Meinungen betrachtet werden können, unterscheiden sie sich diesbezüglich nicht grundlegend von ihren deterministischen Gegenstücken. Der Wert probabilistischer Prognosen für supply chain liegt in der Art und Weise, wie diese feine Struktur genutzt wird, um profitablere Entscheidungen zu ermöglichen. Insbesondere wird in der Regel nicht erwartet, dass probabilistische Prognosen genauer sind als ihre deterministischen Pendants, wenn deterministische Genauigkeitsmetriken zur Bewertung der Prognosequalität herangezogen werden.

Zur Verteidigung der Variabilität

Ungeachtet dessen, was viele Ansätze in supply chain propagieren, wird die Variabilität erhalten bleiben – daher die Notwendigkeit probabilistischer Prognosen. Der erste Irrtum besteht darin, dass Variabilität zwangsläufig etwas Schlechtes für eine supply chain sei; das ist sie nicht. Der zweite Irrtum ist, dass Variabilität eliminiert werden kann; das ist nicht möglich.

Variabilität hat in zahlreichen Situationen positive Auswirkungen auf supply chain. Zum Beispiel werden auf der Nachfrageseite die meisten Branchen von Neuheiten angetrieben, wie Mode, Kulturprodukte, Soft- und Hard-Luxus – ebenso wie „Hit-or-Miss“-Geschäfte. Die meisten neuen Produkte sind keine Erfolge (Misserfolge), aber die, die erfolgreich sind (Hits), erzielen enorme Renditen. Zusätzliche Variabilität ist vorteilhaft, da sie die Wahrscheinlichkeit unerwartet hoher Renditen erhöht, während die Nachteile begrenzt bleiben (im schlimmsten Fall wird das gesamte Inventar abgeschrieben). Der unaufhörliche Strom neuer Produkte, die auf den Markt gebracht werden, sorgt für die ständige Erneuerung der „Hits“, während die alten an Bedeutung verlieren.

Auf der Angebotsseite ist ein Beschaffungsprozess, der hochvariierende Preisangebote sicherstellt, – alles gleich betrachtet – einem alternativen Prozess überlegen, der viel konsistentere (d.h. weniger variable) Preise generiert. Tatsächlich wird die günstigste Option ausgewählt, während die anderen verworfen werden. Es spielt keine Rolle, ob der „durchschnittliche“ bezogene Preis niedrig ist; entscheidend ist es, günstigere Bezugsquellen aufzuspüren. Daher sollte der gute Beschaffungsprozess darauf ausgerichtet sein, die Variabilität zu erhöhen, beispielsweise indem die routinemäßige Erkundung neuer Lieferanten betont wird, anstatt den Beschaffungsprozess auf die etablierten zu beschränken.

Manchmal kann Variabilität aus subtileren Gründen von Vorteil sein. Zum Beispiel, wenn eine Marke in ihren Promotion-Aktivitäten zu vorhersehbar ist, erkennen die Kunden das Muster und beginnen, ihre Kaufentscheidungen zu verzögern, da sie wissen, dass und wann eine Aktion folgt. Die Variabilität – beziehungsweise die Unregelmäßigkeit – der Promotion-Aktivitäten mildert dieses Verhalten bis zu einem gewissen Grad ab.

Ein weiteres Beispiel ist das Vorhandensein von Verwechslungsfaktoren innerhalb der supply chain selbst. Wenn neue Produkte stets mit sowohl einer TV-Kampagne als auch einer Radiokampagne eingeführt werden, wird es statistisch schwierig, die jeweiligen Auswirkungen von TV und Radio zu unterscheiden. Durch Hinzufügen von Variabilität zur jeweiligen Kampagnenintensität, abhängig vom Kanal, wird sichergestellt, dass anschließend mehr statistische Informationen aus diesen Maßnahmen gewonnen werden können, die später in Erkenntnisse für eine bessere Allokation der Marketingressourcen umgewandelt werden können.

Natürlich ist nicht jede Variabilität gut. Lean manufacturing betont zu Recht, dass auf der Produktionsseite der supply chain Variabilität in der Regel schädlich ist, insbesondere wenn es um schwankende Verzögerungen geht. Tatsächlich können LIFO (last-in first-out)-Prozesse versehentlich auftreten, was wiederum die Lieferzeitvariabilität verschärft. In solchen Situationen sollte die zufällige Variabilität durch einen besseren Prozess, manchmal durch bessere Anlagen oder Einrichtungen, beseitigt werden.

Variabilität – auch wenn sie nachteilig ist – ist häufig irreduzierbar. Wie wir im folgenden Abschnitt sehen werden, gehorchen supply chains dem Gesetz der kleinen Zahlen. Es ist wahnhaft zu glauben, dass das Filialniveau jemals zuverlässig vorhergesagt werden kann – aus einer deterministischen Perspektive – während Kunden nicht immer selbst wissen, was sie kaufen werden. Allgemeiner gilt, dass die Reduzierung von Variabilität immer mit Kosten verbunden ist (und eine weitere Verringerung noch mehr kostet), während die marginale Reduktion der Variabilität nur abnehmende Erträge bringt. Daher kann Variabilität, selbst wenn sie reduziert werden kann, praktisch selten vollständig aufgrund der wirtschaftlichen Implikationen eliminiert werden.

Das Gesetz der kleinen Zahlen

Das supply chain Gesetz der kleinen Zahlen kann folgendermaßen formuliert werden: kleine Zahlen herrschen überall in der Kette. Dieses Beobachtungsgesetz resultiert aus den Skaleneffekten und einigen anderen Kräften, die den Großteil der strukturellen Aspekte von supply chains bestimmen:

• Ein Lieferant, der täglich zehntausende Einheiten an Materialien liefert, hat in der Regel Mindestbestellmengen (MOQ) oder Preisstaffeln, die verhindern, dass Bestellungen zu häufig aufgegeben werden. Die Anzahl der an einem Tag an einen Lieferanten übertragenen Bestellungen überschreitet selten eine einstellige Zahl.
• Eine Fabrik, die täglich zehntausende Einheiten produziert, arbeitet in der Regel mit großen Chargen von mehreren tausend Einheiten. Der Produktionsoutput wird meist in ganzen Paletten verpackt. Die Anzahl der Chargen an einem Tag beträgt höchstens eine kleine zweistellige Zahl.
• Ein Lager, das täglich zehntausende Einheiten erhält, wird in der Regel von trucks beliefert, wobei jeder truck seine gesamte Ladung ins Lager entlädt. Die Anzahl der truck-Lieferungen an einem Tag überschreitet selten eine zweistellige Zahl, selbst bei sehr großen Lagern.
• Ein Einzelhandelsgeschäft, das zehntausende Einheiten auf Lager halten kann, teilt sein Sortiment in tausende verschiedene Produktreferenzen auf. Die Anzahl der für jedes Produkt vorrätigen Einheiten überschreitet sehr selten eine einstellige Zahl.
• …

Natürlich ist es immer möglich, die Zahlen aufzublähen, indem man die Maßeinheit ändert. Zum Beispiel, wenn wir statt der Anzahl der Paletten die Anzahl der Gramm einer Palette oder deren Geldwerte in USD-Cents zählen, erscheinen große Zahlen. Das Gesetz der kleinen Zahlen sollte jedoch im Sinne eines sinnvollen Zählens aus der supply chain Perspektive verstanden werden. Während dieses Prinzip in der Theorie recht subjektiv erscheinen mag, ist dies in der Praxis wegen der offensichtlichen diskreten Praktiken moderner supply chains nicht der Fall: Bündel, Kartons, Paletten, Container, trucks …

Dieses Gesetz ist von großer Bedeutung für die Perspektive probabilistischer Prognosen. Zunächst zeigt es auf, dass diskrete Prognosen in supply chain Situationen dominieren, d.h. das zu erwartende (oder zu entscheidende) Ergebnis eine Ganzzahl ist, im Gegensatz zu einem Bruchteil. Probabilistische Prognosen eignen sich besonders für diskrete Situationen, da für jedes diskrete Ergebnis eine Wahrscheinlichkeit abgeschätzt werden kann. Im Gegensatz dazu haben deterministische Prognosen Schwierigkeiten mit diskreten Ergebnissen. Zum Beispiel, was soll es bedeuten, dass der erwartete Tagesabsatz eines Produkts bei 1,3 Einheiten liegt? Einheiten werden nicht in Bruchteilen verkauft. Während aus dieser Aussage sinnvollere, „diskrete“ Interpretationen abgeleitet werden können, ist die probabilistische Entsprechung (z.B. 27% Chance auf 0 Einheiten Nachfrage, 35% Chance auf 1 Einheit Nachfrage, 23% Chance auf 2 Einheiten Nachfrage, etc.) viel eindeutiger, da sie die diskrete Natur des interessierenden Phänomens berücksichtigt.

Zweitens, obwohl probabilistische Prognosen in Bezug auf rohe Rechenressourcen radikal herausfordernder erscheinen mögen, ist dies in der Praxis – gerade aufgrund des Gesetzes der kleinen Zahlen – nicht wirklich der Fall. Tatsächlich gibt es, wenn man auf den oben besprochenen täglichen Produktabsatz zurückkommt, keinen Sinn darin, numerisch zu bewerten, bei welchen Gelegenheiten die Nachfrage an einem bestimmten Tag 100 überschreiten wird. Diese Wahrscheinlichkeiten können auf null – oder einen willkürlich verschwindend kleinen Wert – gerundet werden. Der Einfluss auf die numerische Genauigkeit des supply chain Modells bleibt vernachlässigbar. Als Faustregel ist es vernünftig anzunehmen, dass probabilistische Prognosen etwa drei Größenordnungen mehr Rechenressourcen benötigen als ihre deterministischen Gegenstücke. Dennoch überwiegen die Vorteile in Bezug auf die supply chain performance bei weitem die Kosten der Rechenressourcen.

Genauigkeitsmetriken für probabilistische Prognosen

Unabhängig vom Ausgang zeigt eine einigermaßen gut gestaltete probabilistische Prognose an, dass es tatsächlich eine von Null verschiedene Wahrscheinlichkeit für dieses Ergebnis gab. Dies ist faszinierend, denn auf den ersten Blick mag es so erscheinen, als wären probabilistische Prognosen irgendwie immun gegen die Realität, ähnlich einem Wahrsager, der vage und mehrdeutige prophetische Aussagen macht, die niemals als falsch erwiesen werden können, da der Wahrsager jederzeit eine spätere Erklärung dafür herbeizaubern kann, wie die Prophezeiungen richtig zu interpretieren sind. In Wirklichkeit gibt es mehrere Möglichkeiten, die Qualität einer probabilistischen Prognose quantitativ zu bewerten. Einige dieser Ansätze sind Metriken, die in ihrer Aussagekraft den Metriken zur Bewertung der Genauigkeit deterministischer Prognosen ähneln. Andere Ansätze gehen in radikalere und tiefere Richtungen im Vergleich zur deterministischen Perspektive.

Lassen Sie uns vier verschiedene Ansätze zur Bewertung der Genauigkeit einer probabilistischen Prognose kurz durchgehen:

• die Pinball-Loss-Funktion
• der kontinuierlich bewertete Wahrscheinlichkeits-Score (CRPS)
• die bayesianische Likelihood
• die generative adversarielle Perspektive

Die Pinball-Loss-Funktion bietet eine Genauigkeitsmetrik für eine Quantilschätzung, die aus einer probabilistischen Prognose abgeleitet wird. Zum Beispiel, wenn wir die Lagerbestandsmenge evaluieren möchten, die mit 98%iger Wahrscheinlichkeit größer oder gleich der Kundennachfrage in einem Geschäft für ein bestimmtes Produkt ist, kann diese Menge direkt aus den probabilistischen Prognosen ermittelt werden, indem man einfach die Wahrscheinlichkeiten ab 0 Einheiten Nachfrage, 1 Einheit Nachfrage, … aufsummiert, bis die Wahrscheinlichkeit gerade 98% überschreitet. Die Pinball-Loss-Funktion liefert eine direkte Messung der Qualität dieser verzerrten Schätzung der zukünftigen Nachfrage. Sie kann als ein Werkzeug zur Bewertung der Qualität eines beliebigen Punktes der kumulativen Dichtefunktion der probabilistischen Prognose angesehen werden.

Der kontinuierlich bewertete Wahrscheinlichkeits-Score (CRPS) liefert eine Metrik, die als die „Verschiebungsmenge“ der Wahrscheinlichkeitsmassen interpretiert werden kann, die nötig ist, um die gesamte Wahrscheinlichkeitsmasse auf das beobachtete Ergebnis zu übertragen. Er ist die direkteste Generalisation des mittleren absoluten Fehlers (MAE) in Richtung einer probabilistischen Perspektive. Der CRPS-Wert ist homogen zur Maßeinheit des Ergebnisses selbst. Diese Perspektive kann auf beliebige metrische Räume verallgemeinert werden, anstatt nur auf eindimensionale Situationen, mithilfe dessen, was als „Transporttheorie“ und Monge-Kantorovich-Distanz bekannt ist (was den Rahmen dieses Dokuments sprengt).

Die Likelihood und ihr Kreuzentropie-Verwandter übernehmen die bayesianische Perspektive des geringsten Grades an Überraschung: Je höher die Wahrscheinlichkeit der beobachteten Ergebnisse, desto besser. Zum Beispiel haben wir zwei probabilistische Modelle A und B: Modell A besagt, dass die Wahrscheinlichkeit, 0 Einheiten Nachfrage zu beobachten, an jedem Tag 50% beträgt; Modell B besagt, dass die Wahrscheinlichkeit, 0 Einheiten Nachfrage zu beobachten, an jedem Tag 1% beträgt. Wir beobachten die Nachfrage über 3 Tage und erhalten folgende Beobachtungen: 0, 0, 1. Modell A hatte ungefähr eine 10%-Chance, diese Beobachtungen zu generieren, während Modell B nur circa eine 0,01%-Chance hatte. Somit ist es äußerst unwahrscheinlich, dass Modell B das korrekte Modell ist, verglichen mit Modell A. Die Likelihood weicht von der deterministischen Perspektive eines sinnvollen absoluten Kriteriums zur Bewertung von Modellen ab. Stattdessen liefert sie einen Mechanismus zum Vergleichen von Modellen, der numerisch praktisch nichts anderes leisten kann, als Modelle zu vergleichen.

Die generative adversarielle Perspektive ist die modernste Sichtweise auf das Thema (Ian Goodfellow et al., 2014). Im Wesentlichen besagt diese Perspektive, dass das „beste“ probabilistische Modell jenes ist, das verwendet werden kann, um – monte-carlo-artig – Ergebnisse zu generieren, die von realen Ergebnissen nicht zu unterscheiden sind. Zum Beispiel, wenn wir die historische Liste der Transaktionen in einem lokalen Hypermarkt betrachten würden, könnten wir diese Historie an einem willkürlichen Zeitpunkt in der Vergangenheit abschneiden und das probabilistische Modell dazu verwenden, gefälschte, aber realistische Transaktionen zu erzeugen. Das Modell würde als „perfekt“ gelten, wenn es durch statistische Analysen unmöglich wäre, den Zeitpunkt zu ermitteln, an dem der Datensatz vom „realen“ zu einem „gefälschten“ Zustand übergeht. Der Sinn des generativen adversariellen Ansatzes besteht darin, die Metriken zu „lernen“, die den Fehler eines jeden probabilistischen Modells verschärfen. Anstatt sich auf eine bestimmte Metrik zu konzentrieren, nutzt dieser Ansatz rekursiv Techniken des maschinellen Lernens, um die Metriken selbst zu „lernen“.

Die Suche nach besseren Wegen, die Qualität probabilistischer Prognosen zu bewerten, ist nach wie vor ein aktives Forschungsfeld. Es gibt keine klare Abgrenzung zwischen den beiden Fragen „Wie erzeugt man eine bessere Prognose?“ und „Wie erkennt man, ob eine Prognose besser ist?“. Neuere Arbeiten haben die Grenzen zwischen den beiden erheblich verwischt, und es ist wahrscheinlich, dass die nächsten Durchbrüche weitere Veränderungen in der Betrachtungsweise probabilistischer Prognosen mit sich bringen werden.

Verschwindend kleine Wahrscheinlichkeiten und Log-Likelihood

Sehr kleine Wahrscheinlichkeiten treten natürlich auf, wenn man eine mehrdimensionale Situation durch das Prisma probabilistischer Prognosen betrachtet. Diese kleinen Wahrscheinlichkeiten sind problematisch, weil Computer nicht unendlich präzise Zahlen verarbeiten. Rohe Wahrscheinlichkeitswerte sind häufig „verschwindend“ klein, insofern sie aufgrund begrenzter numerischer Präzision auf null gerundet werden. Die Lösung des Problems besteht nicht darin, die Software auf Berechnungen mit willkürlicher Präzision umzustellen – was in Bezug auf Rechenressourcen sehr ineffizient wäre – sondern den „log-trick“ zu verwenden, der Multiplikationen in Additionen umwandelt. Dieser Trick wird – auf die eine oder andere Weise – von nahezu jeder Software angewendet, die sich mit probabilistischen Prognosen beschäftigt.

Nehmen wir an, dass wir $$X_1, X_2, \ldots, X_n$$ Zufallsvariablen haben, die die Tagesnachfrage für alle $$n$$ unterschiedlichen Produkte eines bestimmten Geschäfts repräsentieren. Seien $$\hat{x}_1, \hat{x}_2, \ldots, \hat{x}_n$$ die jeweils am Ende des Tages beobachtete empirische Nachfrage für jedes Produkt. Für das erste Produkt – bestimmt durch $$X_1$$ – wird die Wahrscheinlichkeit, $$\hat{x}_1$$ zu beobachten, als $$P(X_1=\hat{x}_1)$$ geschrieben. . Nehmen wir nun – etwas vereinfachend, aber zur Verdeutlichung – an, dass alle Produkte bezüglich der Nachfrage strikt unabhängig sind. Die Wahrscheinlichkeit für das gemeinsame Ereignis, $$\hat{x}_1, \hat{x}_2, \ldots, \hat{x}_n$$ zu beobachten, ist:

Wenn $$P(X_k=\hat{x}_k) \approx \tfrac{1}{2}$$ (grob geschätzt) und $$n=10000$$ ist, dann liegt die oben genannte gemeinsame Wahrscheinlichkeit in der Größenordnung von $$\tfrac{1}{{2^{10000}}} \approx 5 \times 10^{-3011}$$, was ein sehr kleiner Wert ist. Dieser Wert unterläuft, d.h. er liegt unterhalb der kleinsten darstellbaren Zahl, selbst wenn man 64-Bit-Gleitkommazahlen betrachtet, die typischerweise für wissenschaftliche Berechnungen verwendet werden.

Der „log-trick“ besteht darin, mit dem Logarithmus des Ausdrucks zu arbeiten, das heißt:

Der Logarithmus wandelt die Reihe von Multiplikationen in eine Reihe von Additionen um, was sich als weitaus numerisch stabiler erweist als eine bloße Reihe von Multiplikationen.

Die Anwendung des „log-tricks“ ist häufig, wenn probabilistische Prognosen im Spiel sind. Die log likelyhood ist buchstäblich der Logarithmus der Likelihood (wie zuvor eingeführt), genau weil die rohe Likelihood üblicherweise numerisch nicht darstellbar wäre, wenn man die gebräuchlichen Arten von Gleitkommazahlen betrachtet.

Algorithmische Varianten probabilistischer Prognosen

Die Frage der computergestützten Erzeugung probabilistischer Prognosen ist fast so umfangreich wie das Gebiet des maschinellen Lernens selbst. Die Abgrenzungen zwischen den beiden Feldern, sofern überhaupt, sind meist eine Frage subjektiver Wahl. Dennoch präsentiert dieser Abschnitt eine eher ausgewählte Liste bemerkenswerter algorithmischer Ansätze, die zur Gewinnung probabilistischer Prognosen verwendet werden können.

Im frühen 20. Jahrhundert, möglicherweise sogar im späten 19. Jahrhundert, entstand die Idee des Sicherheitsbestands, bei der die Nachfrageunsicherheit anhand einer Normalverteilung modelliert wird. Da für andere Wissenschaften, insbesondere der Physik, bereits vorab berechnete Tabellen der Normalverteilung vorlagen, erforderte die Anwendung des Sicherheitsbestands lediglich eine Multiplikation eines Nachfragewertes mit einem „Sicherheitsbestand“-Koeffizienten aus einer bereits bestehenden Tabelle. Anekdotisch enthielten viele supply chain Lehrbücher, die bis in die 1990er Jahre geschrieben wurden, noch Tabellen der Normalverteilung in ihren Anhängen. Leider besteht der Hauptnachteil dieses Ansatzes darin, dass normale Verteilungen keine vernünftige Annahme für supply chains darstellen. Zum einen kann man davon ausgehen, dass nichts in supply chains jemals normal verteilt ist. Zum anderen ist die Normalverteilung eine kontinuierliche Verteilung, die im Widerspruch zur diskreten Natur von supply chain Ereignissen steht (siehe „Das Gesetz der kleinen Zahlen“ oben). Somit haben „Sicherheitsbestände“ zwar technisch gesehen eine probabilistische Komponente, die zugrunde liegende Methodik und die numerischen Rezepte sind jedoch entschieden auf die deterministische Perspektive ausgerichtet. Dieser Ansatz wird hier jedoch der Klarheit halber aufgeführt.

Springen wir in die frühen 2000er Jahre: Ensemble-Lernmethoden – deren wohl bekannteste Vertreter vermutlich Random Forests und Gradient-Boosted Trees sind – lassen sich relativ einfach von ihren deterministischen Ursprüngen auf die probabilistische Perspektive erweitern. Die Grundidee des Ensemble Learnings besteht darin, zahlreiche schwache, deterministische Prädiktoren, wie etwa Entscheidungsbäume, zu einem überlegenen deterministischen Prädiktor zu kombinieren. Es ist jedoch möglich, den Mischprozess so anzupassen, dass statt eines einzelnen Aggregats Wahrscheinlichkeiten gewonnen werden, wodurch die Ensemble-Lernmethode zu einer probabilistischen prognostizierenden Methode wird. Diese Methoden sind nicht-parametrisch und in der Lage, fettleibige und/oder multimodale Verteilungen anzupassen, wie sie üblicherweise in der supply chain zu finden sind. Diese Methoden haben tendenziell zwei wesentliche Nachteile. Zum einen neigt die von dieser Modellsparte konstruierte Dichtefunktion dazu, viele Nullen zu enthalten, was jeden Versuch, die Log-Likelihood-Metrik heranzuziehen, verhindert. Allgemein passen diese Modelle nicht wirklich in die bayessche Perspektive, da neuere Beobachtungen häufig vom Modell als „unmöglich“ (d.h. mit null Wahrscheinlichkeit) deklariert werden. Dieses Problem kann jedoch durch Regularisierungsmethoden¹ gelöst werden. Zum anderen tendieren die Modelle dazu, so groß zu sein wie ein beträchtlicher Anteil des Eingabedatensatzes, und die Operation „predict“ erweist sich fast als genauso rechenintensiv wie die Operation „learn“.

Die hyperparametrischen Methoden, die unter dem Namen „deep learning“ zusammengefasst werden und in den 2010er Jahren explosionsartig aufkamen, waren fast zufällig probabilistisch. In der Tat, während sich der Großteil der Aufgaben, bei denen deep learning wirklich glänzt (z.B. Bildklassifikation), ausschließlich auf deterministische Vorhersagen konzentriert, zeigt sich, dass die Cross-Entropy-Metrik – eine Variante des oben diskutierten Log-Likelihoods – sehr steile Gradienten aufweist, die häufig gut für den stochastischen Gradientenabstieg (SGD) geeignet sind, der im Kern der deep learning Methoden liegt. Somit erweisen sich die deep learning Modelle als probabilistisch konstruiert, nicht weil Wahrscheinlichkeiten von Interesse waren, sondern weil der Gradientenabstieg schneller konvergiert, wenn die Verlustfunktion eine probabilistische Vorhersage widerspiegelt. In Bezug auf deep learning unterscheidet sich die supply chain dadurch, dass sie am tatsächlichen probabilistischen Output des deep learning Modells interessiert ist, während die meisten anderen Anwendungsfälle die Wahrscheinlichkeitsverteilung auf ihren Mittelwert, Median oder Modalwert reduzieren. Die Mixture Density Networks sind eine Art von deep learning Netzwerk, das darauf ausgerichtet ist, komplexe Wahrscheinlichkeitsverteilungen zu erlernen. Das Ergebnis selbst ist eine parametrische Verteilung, möglicherweise bestehend aus Gaußschen Verteilungen. Allerdings kann – im Gegensatz zu Sicherheitsbeständen – eine Mischung aus vielen Gaußverteilungen in der Praxis das fettleibige Verhalten widerspiegeln, das in den supply chains beobachtet wird. Obwohl deep learning Methoden häufig als Stand der Technik betrachtet werden, muss beachtet werden, dass das Erreichen numerischer Stabilität, insbesondere wenn Dichtemischungen involviert sind, nach wie vor als eine Art „dunkle Kunst“ gilt.

Differentierbares Programmieren ist ein Nachfolger des deep learning, der in den allerletzten 2010er Jahren an Popularität gewann. Es teilt viele technische Eigenschaften mit deep learning, unterscheidet sich jedoch deutlich in seinem Fokus. Während deep learning darauf abzielt, willkürlich komplexe Funktionen (z.B. das Spielen von Go) zu erlernen, indem eine große Anzahl einfacher Funktionen (z.B. Faltungsschichten) übereinandergestapelt wird, konzentriert sich das differentierbare Programmieren auf die feinstruktur des Lernprozesses. Die feinste, ausdrucksstärkste Struktur kann – im wahrsten Sinne des Wortes – als ein Programm formuliert werden, das Verzweigungen, Schleifen, Funktionsaufrufe etc. beinhaltet. Differentierbares Programmieren ist von großem Interesse für die supply chain, weil Probleme häufig in stark strukturierter Form auftreten und diese Strukturen den Experten bekannt sind². So kann beispielsweise der Verkauf eines bestimmten Hemdes durch ein Hemd einer anderen Farbe kannibalisiert werden, jedoch nicht durch die Verkäufe eines Hemdes, das drei Größen abweicht. Solche strukturellen Vorannahmen sind entscheidend, um eine hohe Dateneffizienz zu erzielen. Tatsächlich ist aus der Perspektive der supply chain die verfügbare Datenmenge oft sehr begrenzt (vgl. das Gesetz der kleinen Zahlen). Daher hilft es, das Problem strukturell „einzurahmen“, um sicherzustellen, dass die gewünschten statistischen Muster erlernt werden, selbst wenn nur begrenzt Daten zur Verfügung stehen. Strukturierte Vorannahmen tragen zudem dazu bei, Probleme der numerischen Stabilität zu adressieren. Im Vergleich zu Ensemble-Methoden erweisen sich strukturierte Vorannahmen tendenziell als weniger zeitaufwändig als Feature Engineering; auch die Modellwartung wird vereinfacht. Nachteilig ist jedoch, dass das differentierbare Programmieren bis heute eine noch recht junge Perspektive darstellt.

Die Monte-Carlo-Perspektive (1930 / 1940) kann genutzt werden, um probabilistische Vorhersagen aus einem anderen Blickwinkel anzugehen. Die bisher diskutierten Modelle liefern explizite Wahrscheinlichkeitsdichtefunktionen (PDFs). Aus der Monte-Carlo-Perspektive kann jedoch ein Modell durch einen Generator – oder Sampler – ersetzt werden, der zufällig mögliche Ergebnisse (manchmal als „Deviates“ bezeichnet) erzeugt. PDFs können wiederhergestellt werden, indem man die Ergebnisse des Generators mittelt, wobei PDFs häufig vollständig umgangen werden, um den Bedarf an Rechenressourcen zu reduzieren. Tatsächlich wird der Generator oft so konstruiert, dass er datenmäßig erheblich kompakter ist als die PDFs, die er repräsentiert. Die meisten Machine-Learning-Methoden – einschließlich jener, die oben zur direkten Bewältigung probabilistischer Vorhersagen aufgeführt wurden – können dazu beitragen, einen Generator zu erlernen. Generatoren können in Form von niedrigdimensionalen parametrischen Modellen (z.B. Zustandsraummodelle) oder hyperparametrischen Modellen (z.B. den LSTM- und GRU-Modellen im deep learning) auftreten. Ensemble-Methoden werden selten zur Unterstützung generativer Prozesse eingesetzt, da ihre „predict“-Operation aufgrund ihres hohen Rechenaufwands, auf die im Monte-Carlo-Ansatz stark vertraut wird, ineffizient ist.

Arbeiten mit probabilistischen Vorhersagen

Das Ableiten nützlicher Erkenntnisse und Entscheidungen aus probabilistischen Vorhersagen erfordert spezialisierte numerische Werkzeuge. Im Gegensatz zu deterministischen Vorhersagen, bei denen es sich um einfache Zahlen handelt, stellen die Vorhersagen entweder explizite Wahrscheinlichkeitsdichtefunktionen oder Monte-Carlo-Generatoren dar. In der Praxis ist die Qualität der probabilistischen Werkzeuge genauso wichtig wie die Qualität der probabilistischen Vorhersagen. Ohne diese Werkzeuge verkommt die Nutzung der probabilistischen Vorhersagen zu einem deterministischen Prozess (mehr dazu im Abschnitt „Antipatterns“ weiter unten).

Zum Beispiel sollte das Tooling in der Lage sein, Aufgaben wie folgt auszuführen:

• Kombiniere die unsichere Produktionslieferzeit mit der unsicheren Transportlieferzeit, um die „gesamte“ unsichere Lieferzeit zu ermitteln.
• Kombiniere die unsichere Nachfrage mit der unsicheren Lieferzeit, um die „gesamte“ unsichere Nachfrage zu bestimmen, die durch den in Kürze zu bestellenden Bestand gedeckt werden soll.
• Kombiniere die unsicheren Rücksendungen von Bestellungen (ecommerce) mit dem unsicheren Ankunftsdatum der sich im Transit befindlichen Lieferantenbestellung, um die unsichere Kundenlieferzeit zu erhalten.
• Ergänze die durch eine statistische Methode erstellte Nachfrageprognose um ein Tail-Risiko, das manuell aus einem übergeordneten Verständnis eines in den historischen Daten nicht abgebildeten Kontexts (z. B. einer Pandemie) abgeleitet wurde.
• Kombiniere die unsichere Nachfrage mit einem unsicheren Zustand des Bestands hinsichtlich des Verfallsdatums (Lebensmittelhandel), um den unsicheren Restbestand am Tagesende zu ermitteln.
• …

Sobald alle probabilistischen Vorhersagen – und nicht nur die der Nachfrage – richtig kombiniert wurden, sollte die Optimierung der supply chain Entscheidungen erfolgen. Dies beinhaltet eine probabilistische Perspektive auf die Nebenbedingungen sowie die Score-Funktion. Dieser Aspekt des Toolings geht jedoch über den Umfang des vorliegenden Dokuments hinaus.

Es gibt zwei grundlegende „Varianten“ von Werkzeugen zur Arbeit mit probabilistischen Vorhersagen: erstens Algebren über Zufallsvariablen, zweitens probabilistisches Programmieren. Diese beiden Varianten ergänzen sich, da sie nicht dieselbe Mischung aus Vor- und Nachteilen aufweisen.

Eine Algebra von Zufallsvariablen arbeitet typischerweise mit expliziten Wahrscheinlichkeitsdichtefunktionen. Die Algebra unterstützt die üblichen arithmetischen Operationen (Addition, Subtraktion, Multiplikation etc.), übertragen auf ihre probabilistischen Gegenstücke, wobei Zufallsvariablen häufig als statistisch unabhängig behandelt werden. Sie gewährleistet eine numerische Stabilität, die fast an die ihres deterministischen Pendants (d.h. einfacher Zahlen) heranreicht. Alle Zwischenergebnisse können zur späteren Verwendung gespeichert werden, was sich bei der Organisation und Fehlersuche in der Datenextraktions-Pipeline als sehr praktisch erweist. Nachteilig ist, dass der Ausdrucksreichtum dieser Algebren tendenziell begrenzt ist, da es üblicherweise nicht möglich ist, alle feinen bedingten Abhängigkeiten zwischen den Zufallsvariablen abzubilden.

Probabilistisches Programmieren übernimmt eine Monte-Carlo-Perspektive auf das Problem. Die Logik wird einmal geschrieben – meist ausgehend von einer vollständig deterministischen Perspektive –, aber dann vielfach durch das Tooling (d.h. den Monte-Carlo-Prozess) ausgeführt, um die gewünschten Statistiken zu sammeln. Maximale Ausdruckskraft wird durch „programmatische“ Konstrukte erreicht: Es ist möglich, beliebige, komplexe Abhängigkeiten zwischen den Zufallsvariablen zu modellieren. Das Schreiben der Logik mittels probabilistischen Programmierens ist im Vergleich zu einer Algebra von Zufallsvariablen tendenziell etwas einfacher, da die Logik nur mit gewöhnlichen Zahlen arbeitet. Nachteilig ist jedoch, dass stets ein Kompromiss zwischen numerischer Stabilität (mehr Iterationen liefern bessere Präzision) und Rechenressourcen (mehr Iterationen kosten mehr) besteht. Zudem sind Zwischenergebnisse typischerweise nicht unmittelbar zugänglich, da ihre Existenz nur vorübergehend ist – genau, um den Druck auf die Rechenressourcen zu verringern.

Jüngste Arbeiten im deep learning deuten zudem darauf hin, dass es über die beiden oben präsentierten Ansätze hinaus weitere Methoden gibt. So bieten beispielsweise Variational Autoencoders Perspektiven, Operationen in latenten Räumen durchzuführen, was zu beeindruckenden Ergebnissen führt, während gleichzeitig sehr komplexe Transformationen an den Daten vorgenommen werden (z.B. das automatische Entfernen von Brillen aus einem Porträtfoto). Obwohl diese Ansätze konzeptionell sehr faszinierend sind, haben sie – bisher – in der praktischen Anwendung bei supply chain Problemen kaum an Relevanz gewonnen.

Visualisierung probabilistischer Vorhersagen

Die einfachste Methode, eine diskrete Wahrscheinlichkeitsverteilung zu visualisieren, ist ein Histogramm, bei dem die vertikale Achse die Wahrscheinlichkeit und die horizontale Achse den Wert der interessierenden Zufallsvariablen anzeigt. So kann beispielsweise eine probabilistische Vorhersage einer Lieferzeit dargestellt werden als:

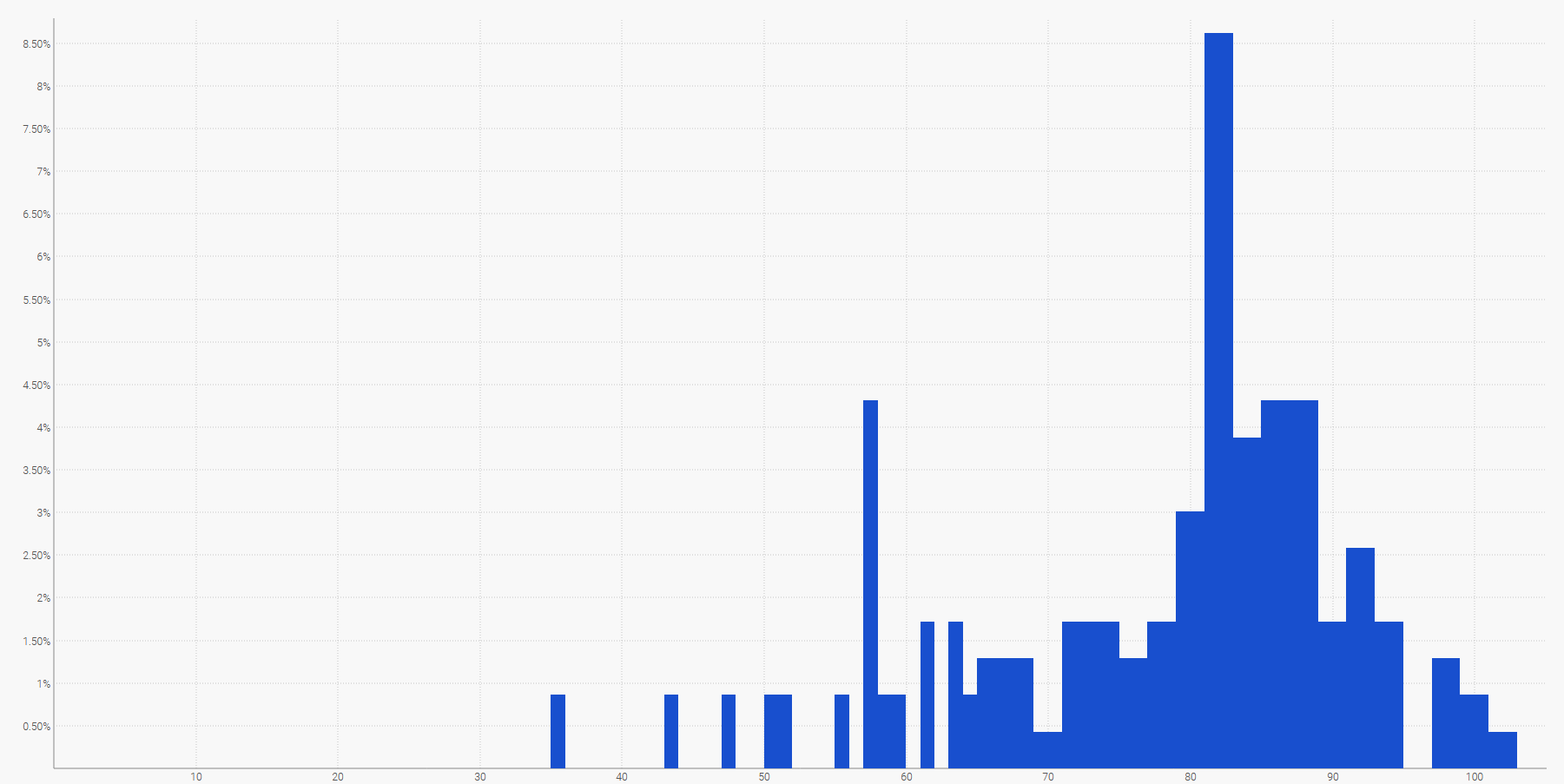
Die zukünftige Nachfrage, über einen festgelegten Zeitraum aufsummiert, kann ebenfalls durch ein Histogramm dargestellt werden. Allgemein eignet sich das Histogramm gut für alle eindimensionalen Zufallsvariablen über $${ℤ}$$, der Menge der relativen Ganzzahlen.

Die Visualisierung des probabilistischen Äquivalents einer gleichmäßig verteilten Zeitreihe – d.h. einer Größe, die sich über diskrete, gleich lange Zeiträume ändert – ist bereits weitaus herausfordernder. Tatsächlich gibt es im Gegensatz zur eindimensionalen Zufallsvariablen keine kanonische Darstellung einer solchen Verteilung. Beachte, dass die Zeiträume nicht als unabhängig angenommen werden können. Zwar ist es möglich, eine „probabilistische“ Zeitreihe darzustellen, indem man eine Reihe von Histogrammen – jeweils eines pro Zeitraum – anordnet, jedoch würde diese Darstellung den tatsächlichen Ablauf der Ereignisse in der supply chain stark verzerren.

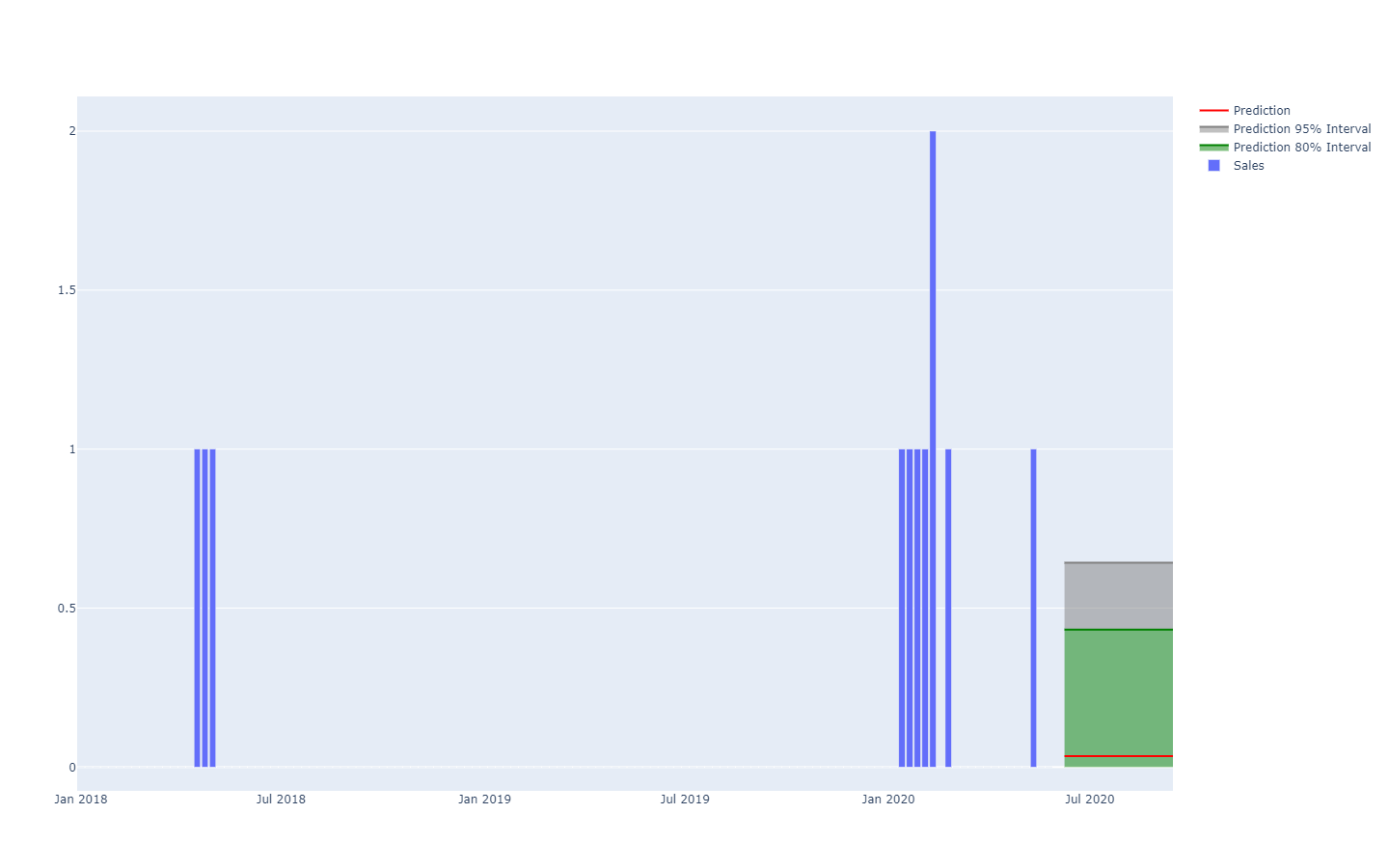
Zum Beispiel ist es nicht allzu unwahrscheinlich, dass ein neu eingeführtes Produkt gute Leistungen erbringt und hohe Verkaufszahlen erzielt (ein Hit). Ebenso wenig ist es unwahrscheinlich, dass dasselbe neu eingeführte Produkt scheitert und niedrige Verkaufszahlen erzielt (ein Fehlschlag). Allerdings sind enorme tägliche Schwankungen zwischen Hit- und Fehlschlag-Verkaufszahlen äußerst unwahrscheinlich.

Vorhersageintervalle, wie sie in der supply chain Literatur häufig vorkommen, sind etwas irreführend. Sie neigen dazu, Situationen mit geringer Unsicherheit zu betonen, die nicht repräsentativ für tatsächliche supply chain Situationen sind;

Beachte, dass diese Vorhersageintervalle genau die Wahrscheinlichkeitsverteilungen sind, nebeneinander angeordnet und mit einem Farbschema versehen, das bestimmte Quantilschwellen hervorhebt.

Eine bessere Darstellung – also eine, die die starken Abhängigkeiten zwischen den Zeiträumen nicht verfälscht – besteht darin, die kumulativen Werte über die Zeit zu betrachten, deren Quantile zu ermitteln und anschließend zu differenzieren, um die Zuwächse pro Zeitraum wieder zu gewinnen (siehe die erste Darstellung einer probabilistischen Vorhersage zu Beginn dieses Artikels). Die Visualisierung bleibt gleich, jedoch unterscheidet sich die zugrunde liegende Semantik. Wir betrachten nun Quantile über Szenarien, die die äußerst günstigen (bzw. ungünstigen) Szenarien aufzeigen.

Antipatterns bei probabilistischen Vorhersagen

Probabilistische Vorhersagen fordern die Art und Weise heraus, wie viele Menschen intuitiv über die Zukunft denken. In diesem Abschnitt werden einige der am häufigsten missverstandenen Aspekte probabilistischer Vorhersagen behandelt.

Es gibt keine ‚unvorhersehbaren‘ Ereignisse

Aus deterministischer Sicht ist es unmöglich, den Ausgang der Lotterie vorherzusagen, da die Chance, richtig zu liegen, „eins zu eine Million“ beträgt. Aus probabilistischer Sicht ist das Problem jedoch trivial: Jedes Los hat eine „eins zu eine Million“ Chance zu gewinnen. Die sehr hohe Varianz des Ergebnisses sollte nicht mit einer grundsätzlichen Unkenntlichkeit des Phänomens selbst verwechselt werden, das durchaus vollständig verstanden werden kann, wie es bei einer Lotterie der Fall ist. Probabilistisches Forecasting dient dazu, die Varianz zu quantifizieren und zu strukturieren, nicht dazu, sie zu eliminieren.

Es gibt keine ‚normalen‘ Verteilungen

Es gibt keine ‚normalen‘ Verteilungen

Normalverteilungen, auch bekannt als Gaußverteilungen, sind in sowohl supply chain- als auch Physiklehrbüchern allgegenwärtig. Doch was menschliche Angelegenheiten betrifft, ist so gut wie nichts „normal“ verteilt. Normalverteilungen machen per Design große Abweichungen (im Vergleich zu den durchschnittlichen Abweichungen) äußerst selten, bis zu dem Punkt, an dem sie vom Modell als schlicht unmöglich ausgeschlossen werden – d.h. Wahrscheinlichkeiten von weniger als eins zu einer Milliarde. Nachfrage, Lieferzeit, Rücksendungen sind viele Muster, die kategorisch nicht normal verteilt sind. Der einzige Vorteil von Normalverteilungen besteht darin, dass sie sich hervorragend dazu eignen, Lehrbuchübungen für Studierende zu konzipieren, da sie expliziten analytischen Lösungen zugänglich sind.

Auswählen einzelner Wahrscheinlichkeiten

Wenn man mit einer Wahrscheinlichkeitsverteilung konfrontiert wird, ist es verlockend, einen einzelnen Punkt der Verteilung – möglicherweise den Mittelwert oder den Median – herauszupicken und sich auf diese Zahl zu stützen. Dieser Vorgang widerspricht dem eigentlichen probabilistischen Charakter der Prognose. Wahrscheinlichkeiten sollten nicht auf einen einzigen Punktschätzwert zusammengefasst werden, denn egal welcher Punkt gewählt wird, führt dies zu einem massiven Informationsverlust. Somit sollen die Wahrscheinlichkeiten – wenn auch etwas beunruhigend – so lange wie möglich in ihrer Gesamtheit erhalten bleiben. Der Moment der Zusammenfassung ist typischerweise die endgültige supply chain Entscheidung, die die Erträge maximiert, während sie sich unsicheren Zukunftsaussichten gegenübersieht.

Entfernen statistischer Ausreißer

Die meisten klassischen numerischen Methoden – die fest in der deterministischen Perspektive der Prognosen verankert sind (z. B. gleitende Durchschnitte) – verhalten sich äußerst problematisch, wenn sie auf statistische Ausreißer stoßen. Daher etablieren viele Unternehmen Prozesse, um die historischen Daten manuell von diesen Ausreißern zu „reinigen“. Dieser Bedarf an einem solchen Reinigungsprozess weist jedoch lediglich auf die Mängel dieser numerischen Methoden hin. Im Gegenteil, statistische Ausreißer sind ein wesentlicher Bestandteil der probabilistischen Prognose, da sie dazu beitragen, ein besseres Bild davon zu erhalten, was am Ende der Verteilung geschieht. Anders ausgedrückt: Diese Ausreißer sind der Schlüssel, um die Wahrscheinlichkeit des Auftretens weiterer Ausreißer zu quantifizieren.

Mit dem Schwert in ein Schusswaffengefecht gehen

Zur Manipulation von Wahrscheinlichkeitsverteilungen ist spezialisierte Software erforderlich. Die Erstellung der probabilistischen Prognose ist nur ein Schritt unter vielen, um einen tatsächlichen Mehrwert für das Unternehmen zu liefern. Viele supply chain practitioners verwerfen probabilistische Prognosen letztlich aufgrund fehlender geeigneter Werkzeuge, um damit etwas anzufangen. Zahlreiche Enterprise software vendors haben den Anschluss gefunden und behaupten nun, „probabilistische Prognosen“ zu unterstützen (neben „KI“ und der „Blockchain“), sind jedoch nie über die kosmetische Implementierung einiger probabilistischer Modelle hinausgegangen (vgl. den obigen Abschnitt). Das Vorweisen eines probabilistischen Prognosemodells ist nahezu wertlos ohne die umfangreichen Werkzeuge, um seine numerischen Ergebnisse zu nutzen.

Notizen