Prix magique

Le prix magique est une méthode de tarification visant à maximiser le profit en effectuant de micro-ajustements dans la structure des prix. Elle repose sur l’hypothèse que les consommateurs sont réticents aux calculs et ne liront donc que les premiers chiffres d’un prix lors de leur décision d’achat. Selon cette méthode, l’information pertinente d’un prix donné ne concerne généralement pas les derniers chiffres, mais plutôt les premiers, ou en d’autres termes, l’ordre de grandeur des nombres. Par exemple, le prix de 17,99 $ ressemble davantage à 17 $ qu’à 18 $.

Cette méthode de tarification est très répandue. Selon Judith Holdershaw et al, plus de 90% des prix en Nouvelle-Zélande se terminent par un chiffre supérieur à 5, et 60% d’entre eux se terminent par “9”.

Pourquoi utiliser le prix magique?

La stratégie du prix magique repose sur le fait que les consommateurs attachent une grande importance à leur temps lorsqu’ils évaluent les prix. Le coût en temps augmente à mesure que l’on examine chaque chiffre supplémentaire d’un nombre donné, ce qui signifie que, lors de l’examen d’un prix, les premiers chiffres ont plus de poids que les derniers. Nous pouvons définir un taux de pertinence pour chaque chiffre et ainsi définir les deux concepts de “prix perçu” et de “prix réel”.

Un consommateur doit évaluer le prix de 1743,99 $. Le premier chiffre porte plus de 50 % de l’information car 1000 $ représente plus de 50 % du prix, ce qui signifie que le consommateur lira et comprendra clairement ce chiffre. Étant donné que le deuxième chiffre (700 $) porte environ 40 % de la signification du prix, le consommateur lira également ce nombre. Ensuite, le troisième chiffre (40 $) ne représente que 2 % de l’information globale sur le prix et est donc moins pertinent. Dans ce cas, le prix pertinent pour le consommateur est soit 1740,00 $, soit 1700,00 $, selon le seuil de pertinence souhaité.

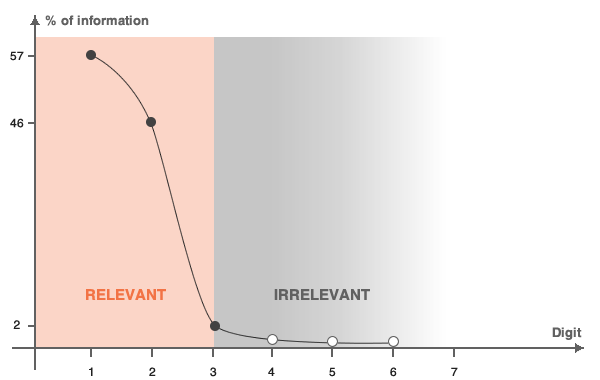
Une fois que nous avons défini la partie pertinente ou, en d’autres termes, la partie perçue d’un prix, nous pouvons maximiser le profit sur ce chiffre en remplaçant tous les chiffres non pertinents par des “9”. L’ajout de chiffres “non pertinents” au prix perçu conservera néanmoins le même prix perçu, et n’aura donc aucun impact sur la demande ou les ventes de cet article en particulier. Les chiffres additionnels – non perçus – du prix seront entièrement convertis en profit. C’est le cas des 99 centimes dans l’exemple de 1743,99 $ ci-dessus. Étant donné le prix global du produit, les 99 centimes n’influencent pas la décision d’achat du consommateur et sont donc entièrement convertis en profit.

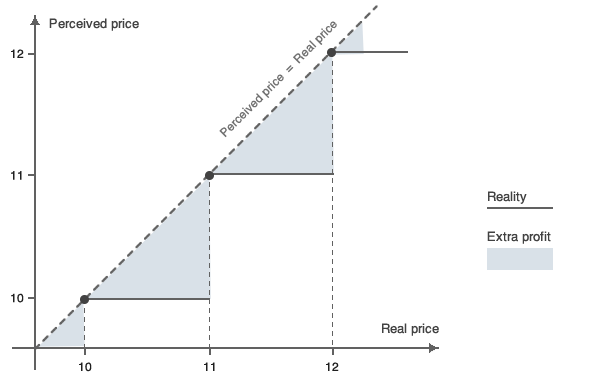
Un problème à considérer lors de l’utilisation de cette méthode est lié aux tranches de prix. Aujourd’hui, la plupart des sites de e-commerce offrent la possibilité de filtrer les produits par tranches de prix telles que 50 $-99 $. Fixer un prix à 99,99 $ au lieu de 100 $ implique de se situer dans la tranche de prix 50-99 $, ce qui peut, potentiellement, avoir un impact positif sur la demande.

Cette méthode a également deux effets dans le domaine comptable. Premièrement, si tous les prix se terminent par “.99”, il est facile de calculer le montant des ventes quotidiennes. Par exemple, si le flux de trésorerie en fin de journée se termine par “.38”, cela signifie que 62 ventes (ou 162, 262, etc.) ont eu lieu ce jour-là. Deuxièmement, cette méthode de tarification rend plus difficile le vol de liquidités dans les entreprises où la caisse est facilement accessible au personnel (par exemple, dans les supermarchés). Il faudrait prélever un montant composé d’une valeur se terminant par “.99” de la caisse afin de le faire ressembler à une vente, ce qui est plus difficile à réaliser avec des prix se terminant par “.00”.

Fonctionne-t-il ?

Observe-t-on un décalage de la demande en comparant les prix se terminant par “.99” et par “.00” ? Si tel est le cas, cela signifie que le signal porté par le prix “.99” est plus fort que le centime qui les sépare.

Selon Guéden et al, cet effet peut en effet être assez significatif. Leur étude se concentre sur une petite pizzeria-grill en France. Une liste de neuf plats principaux était proposée dans le restaurant et incluait cinq pizzas différentes. L’effet de la terminaison de prix d’une pizza a été testé. Pendant 2 semaines, toutes les pizzas étaient proposées avec un prix se terminant par “.00” (c’est-à-dire 9,00 Euro) tandis que pendant 2 autres semaines, une pizza cible était proposée avec un prix se terminant par “9” (c’est-à-dire 8,99 Euro) alors que les quatre autres étaient proposées avec un prix se terminant par “.00”. Enfin, une troisième période de 2 semaines a été testée où toutes les pizzas étaient proposées avec un prix se terminant par “9”. Les résultats ont montré qu’une augmentation du choix de la pizza cible par les clients était observée lorsque le prix de cet article se terminait par un 9 et que les prix des autres articles se terminaient par zéro. Aucune différence dans le choix de la pizza cible n’a été observée lorsque tous les articles étaient présentés avec le même type de terminaison (9 ou 0). Cela montre que, comparativement, l’effet des prix se terminant par neuf sur la part de marché peut en effet être très significatif.

Schindler et Kibarian ont également mené une étude sur les effets du prix magique, mais cette fois à plus grande échelle. Plus précisément, ils ont examiné les terminaisons de prix pour un site de e-commerce de mode féminine, où ils ont comparé l’effet sur les ventes des prix se terminant par “.88”, “.99” et “.00”. Les ventes des articles à prix se terminant par “.99” se sont avérées être supérieures de 8 % par rapport aux prix se terminant par “.00”. Ce n’était toutefois pas le cas pour les prix se terminant par “.88”. Selon la théorie du prix magique, la perception associée aux prix se terminant par “.99” et “.88” ne devrait pas être différente et devrait donc entraîner la même demande client. Cependant, les preuves empiriques démontrent qu’un meilleur signal d’achat est obtenu avec les prix se terminant par “.99”. En ce qui concerne le prix magique, il semble que l’élément déterminant soit le ressenti du consommateur à l’égard des produits “bien tarifés”. Et c’est ce qui conduit par conséquent à une augmentation de sa volonté d’acheter.

Quels sont les principaux problèmes du prix magique ?

Le prix magique repose fortement sur l’hypothèse que les consommateurs ont tendance à prendre les prix impairs pour ce qu’ils apparaissent et n’investissent pas beaucoup de temps ou d’effort pour réellement comprendre ce qui se cache derrière les derniers chiffres d’un prix donné. Cependant, cette hypothèse n’est pas toujours vraie. Pour donner un exemple, regardons le secteur de l’immobilier. Si nous nous basons sur l’hypothèse du prix magique décrite ci-dessus, un consommateur ne devrait techniquement pas faire de grande différence entre une même propriété affichée à 1 860 000,99 $ ou à 1 810 000,99 $. Néanmoins, la différence de 50 000 $ entre les deux prix est très significative et est fort peu susceptible d’être négligée par l’acheteur. En conséquence, cet exemple démontre que le prix magique ne fonctionne effectivement pas dans toutes les circonstances.

Un autre problème est lié aux effets psychologiques associés au prix magique. Les produits dont le prix se termine par “.99” sont souvent perçus comme des articles promotionnels ou bon marché. Par conséquent, il est probable que la modification du dernier chiffre d’un prix change la perception de la qualité du produit. Si nous supposons que la qualité estimée du produit a un impact sur la demande, alors une baisse perçue de la qualité associée aux prix se terminant par “.99” entraîne une demande moindre et donc des profits moindres.

Pour illustrer, les consommateurs peuvent considérer qu’une cafetière affichée à moins de 20 $ n’est pas assez chère et voir ce prix comme un signe de faible qualité. Par conséquent, fixer le prix de la cafetière à 19,99 $ réduira considérablement la demande, démontrant l’inefficacité du prix magique dans ce cas précis.

Références

• Anderson E. T. & Simester D. I., “Indices de prix et connaissance du prix par le client”, 2008
• Guéguen N., Jacob C., Legoherel P. & Ngobo P., “Les prix se terminant par neuf et le comportement des consommateurs : une étude de terrain dans un restaurant”, International Journal of Hospitality Management, 2009
• Holdershaw J., Gendall P. & Garland R., “La généralisation de l’utilisation du prix magique dans le secteur de la distribution”, Marketing Bulletin, 1997
• Nyström H., Tarification de détail. Une approche économique et psychologique intégrée, 1970
• Schindler R. M. & Kirbarian T. M., “Réponse accrue des ventes consommateurs grâce à l’utilisation de prix se terminant par 99”, Journal of Retailing, 1996