00:54 イントロダクション
02:25 進歩の本質について
05:26 これまでの経緯
06:10 いくつかの定量的原則:観察原則
07:27 エントロピーを用いた「藁の中の針」問題の解決
14:58 サプライチェーンの集団はZipf分布に従う
22:41 サプライチェーンの意思決定では小さな数値が支配的
29:44 サプライチェーンにはあらゆる場所にパターンが存在する
36:11 いくつかの定量的原則:最適化原則
37:20 サプライチェーンの問題を解決するには5~10回のラウンドが必要
44:44 古いサプライチェーンは一方向に準最適である
49:06 局所的なサプライチェーンの最適化は問題を先送りにするだけ
52:56 より良い問題はより良い解決策に勝る
01:00:08 結論
01:02:24 今後の講義と聴衆からの質問
説明
サプライチェーンは電磁気学のように明確な定量的法則によって特徴付けることはできませんが、一般的な定量的原則は観察することができます。「一般的」とは、ほぼすべてのサプライチェーンに適用可能であることを意味します。そのような原則を明らかにすることは、サプライチェーンの数値レシピによる予測的最適化のためのエンジニアリングを促進するのに用いられるだけでなく、これらの数値レシピ全体をより強力にするためにも利用できるため、非常に重要です。ここでは、いくつかの観察原則といくつかの最適化原則という、2つの短い原則リストを検討します.
完全な書き起こし

皆さん、こんにちは。このサプライチェーン講義シリーズへようこそ。私はジョアンネス・ヴェルモレルです。本日は「サプライチェーンのための定量的原則」をご紹介します。YouTubeでライブ視聴されている方は、いつでもチャットで質問を投稿してください。ただし、講義中に質問を読むことはありません。講義の最後にチャットに戻り、できる限り多くの質問にお答えします.
定量的原則は非常に注目すべきものであり、サプライチェーンにおいては、最初の講義で見たように、オプショナリティの制御が伴います。これらの選択肢のほとんどは定量的な性質を持っています。いくら購入するか、生産量、在庫の移動量、さらには価格設定 ― 価格を上げるか下げるか ― を決定しなければなりません。したがって、サプライチェーンの数値レシピの改善を促す定量的原則は極めて重要です.
しかしながら、もし現代のほとんどのサプライチェーンの権威や専門家に、サプライチェーンにおける核心的な定量的原則は何かと尋ねたならば、多くの場合、改善された時系列予測のための一連の技術やそれに類するものという回答が得られると推測されます。私個人の見解としては、これは興味深くかつ重要なものである一方で、本質を捉え損ねていると考えています。進歩そのものの本質、すなわち何が進歩であり、サプライチェーンにおいてどのように進歩を実現できるかという点に、根本的な誤解があると信じています。例を挙げて説明しましょう.

6000年前に車輪が発明され、6000年後に車輪付きスーツケースが発明されました。この発明はこの特許によって示され、1949年に発明されたとされています。車輪付きスーツケースが発明された時点では、すでに原子力を利用し、最初の数発の原爆を爆発させていました.
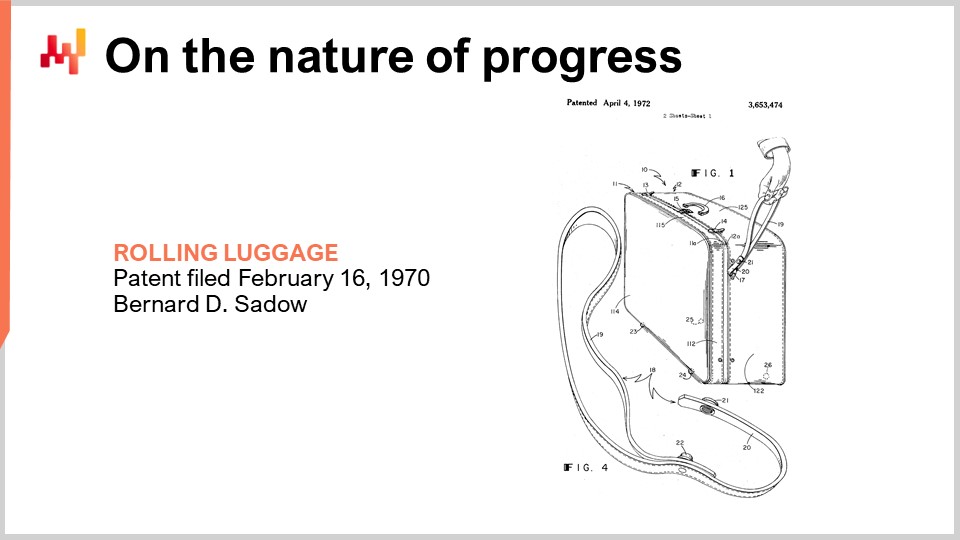
それから20年後の1969年、人類は月に初めて人を送りました。翌年、この特許に示されるように、僅かに改善されたハンドル(リードのような形状)を備えた車輪付きスーツケースが登場しました。しかし、依然としてあまり優れたものではありませんでした.

そしてさらに20年後、すでに民間利用が10年以上にわたって行われているGPS(全地球測位システム)が存在する中で、車輪付きスーツケースに適したハンドルが遂に発明されました.
ここで注目すべき教訓は少なくとも2つあります。まず、進歩に関して明らかな時間の矢印というものは存在しません。進歩は極めてカオス的かつ非線形な方法で進行し、他の分野で起こっていることから一つの分野で起こるべき進歩を評価するのは非常に困難です。この点は本日留意すべき要素の一つです.
次に、進歩と洗練を混同してはならないという点です。圧倒的に優れたものであっても、非常にシンプルである場合もあります。スーツケースの例を挙げれば、一度そのデザインを見れば、全く自明で分かりやすいものに見えるでしょう。しかし、それが容易に解決できた問題だったでしょうか?決してそうではありません。供給チェーン管理が解決の難しい問題であったという簡単な証拠は、高度な産業文明がこの問題に取り組むのに40年以上を要したという事実です。進歩は洗練の規則に従わないという点で欺瞞的であり、進歩が起こる前の世界がどのようなものであったかを特定するのは非常に困難です。なぜなら、進歩が起こるとともに世界観そのものが変わってしまうからです.

さて、サプライチェーンの議論に戻りましょう。これは本序章における6回目で最後の講義です。サプライチェーン講義全体の包括的な計画は、Lokadのウェブサイトでオンラインにてご確認いただけます。2週間前、私はサプライチェーンの20世紀におけるトレンドを、純粋な定性的視点からご紹介しました。本日は、これに対抗する形で、かなり定量的な視点からこの問題群にアプローチします.

本日は、一連の原則について検討します。ここでいう原則とは、あらゆるサプライチェーンの数値レシピの設計を改善するために使用できるものを意味します。我々は一般化を目指しており、そのため、すべてのサプライチェーンやそれらを改善するためのあらゆる数値手法にとって最も重要なものを見出すのは非常に困難です。ここでは、観察原則と最適化原則という、2つの短い原則リストを検討します.
観察原則は、サプライチェーンについて定量的に知識や情報を得る方法に適用されます。一方、最適化原則は、サプライチェーンに関する定性的な知識を得た後、具体的にはこれらの原則をどのように活用して最適化プロセスを改善するかに関係します.
サプライチェーンの観察を始めましょう。人々がまるで自分の目で直接サプライチェーンを観察できるかのように語るとき、私は非常に不思議に感じます。これはサプライチェーンの現実を大きく歪めた認識だと思います。サプライチェーンは、その設計上、定量的な観点から直接に人間の目で観察することはできません。というのも、サプライチェーンは地理的に分散しており、潜在的に数千のSKUや数万のユニットが関与するからです。人間の目では、今日のサプライチェーンの状態しか観察できず、過去の状態は捉えられません。サプライチェーンに関連する数字のうち、ほんの一部以上の数字を記憶することはできません.
サプライチェーンを観察したいときは、必ずエンタープライズソフトウェアを介して間接的に観察することになります。これはサプライチェーンを捉える非常に特定の方法です。サプライチェーンに関して定量的に行えるすべての観察は、この特定の手段であるエンタープライズソフトウェアを通じて行われます.
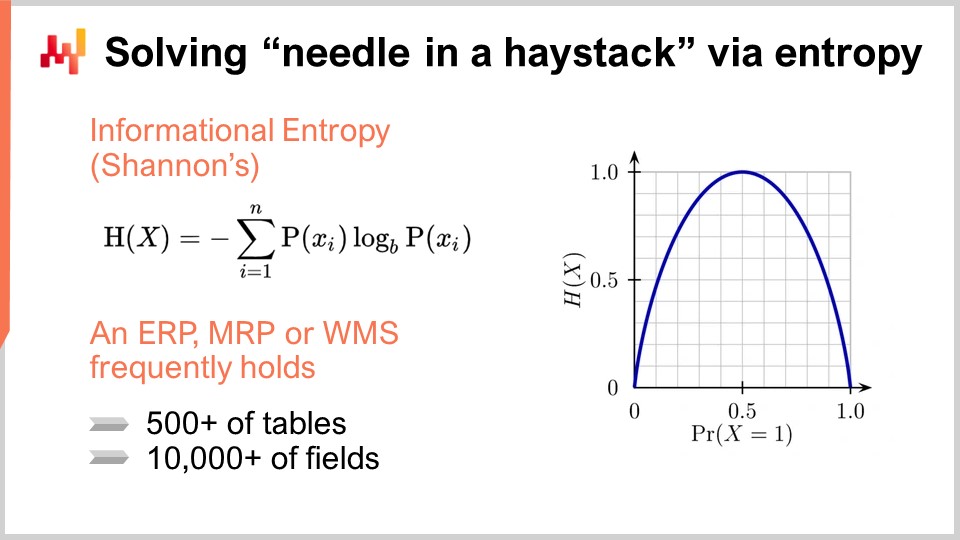
典型的なエンタープライズソフトウェアの特徴を見てみましょう。ほとんどのソフトウェアがそのように設計されているように、当該ソフトウェアにはデータベースが含まれます。このソフトウェアは大体500以上のテーブルと10,000のフィールド(フィールドは本質的にはテーブルのカラムです)を持つ可能性があります。入力点として、このシステムは膨大な量の情報を含んでいるかもしれません。しかし、多くの場合、サプライチェーンにとって実際に関連するのは、このソフトウェア複雑性全体のほんの一部に過ぎません.
ソフトウェアベンダーは、あらゆる多様な状況を考慮してエンタープライズソフトウェアを設計します。特定のクライアントを見ると、実際に使用されるのはソフトウェア機能全体のほんの一部である可能性が高いです。つまり、理論上は10,000のフィールドを探索できるかもしれませんが、実際には企業はごく僅かなフィールドしか使用していません.
課題は、存在しない、あるいは無関係なデータから関連情報をどのように選び出すかにあります。サプライチェーンはエンタープライズソフトウェアを通してしか観察できず、場合によっては複数のソフトウェアが関与することもあります。場合によっては、フィールドが一度も使用されず、データが一定でゼロやヌルばかりであることもあります。このような場合、そのフィールドは情報を全く含まないため、容易に除外できます。しかし実際には、偶然にでも利用された多くの機能があるため、この方法で除外できるフィールドの数はわずか約10%に過ぎないかもしれません.
一度も有意義に使用されたことのないフィールドを識別するために、情報エントロピーと呼ばれるツールに注目できます。シャノンの情報理論に馴染みのない方には、この用語は威圧的に感じられるかもしれませんが、実際は見た目ほど複雑ではありません。情報エントロピーは、シンボルの並びとして定義される信号に含まれる情報量を定量化することに関するものです。例えば、あるフィールドが「真」または「偽」の2種類の値のみを含み、そのカラムがこれらの値をランダムに変動させる場合、そのカラムは大量のデータを含むといえます。対照的に、100万行中たった一行だけが真で、残りがすべて偽である場合、データベースのそのフィールドはほとんど情報を含んでいないことになります.
情報エントロピーは非常に興味深い概念です。なぜなら、データベースの各フィールドに存在する情報量をビット単位で定量化できるからです。解析を行うことで、情報量の多い順から少ない順にフィールドを順位付けし、サプライチェーン最適化の目的に対してほとんど情報を持たないフィールドを除外することが可能となります。情報エントロピーは一見複雑に見えますが、理解するのはそれほど難しくありません.

例えば、ドメイン固有のプログラミング言語を考えると、我々は情報エントロピーを集約機能として実装しています。data.csvというフラットファイルの3列のデータのようなテーブルを用いることで、各カラムに存在するエントロピーの概要をプロットできます。このプロセスにより、どのフィールドが最も少ない情報しか含まないかを容易に判断し、除外することが可能です。エントロピーを指標として使用することで、プロジェクトを迅速に開始でき、何年もかかることがなくなります.
次の段階に進み、サプライチェーンについて最初の観察を行い、何を期待するかを考えます。自然科学では、標準的な期待値として正規分布(ベルカーブ、ガウス分布とも呼ばれる)が挙げられます。例えば、20歳の男性の身長や体重は正規分布に従います。生物の領域では、多くの測定値がこのパターンに従います。しかし、サプライチェーンに関しては、興味深い正規分布はほとんど見られません.
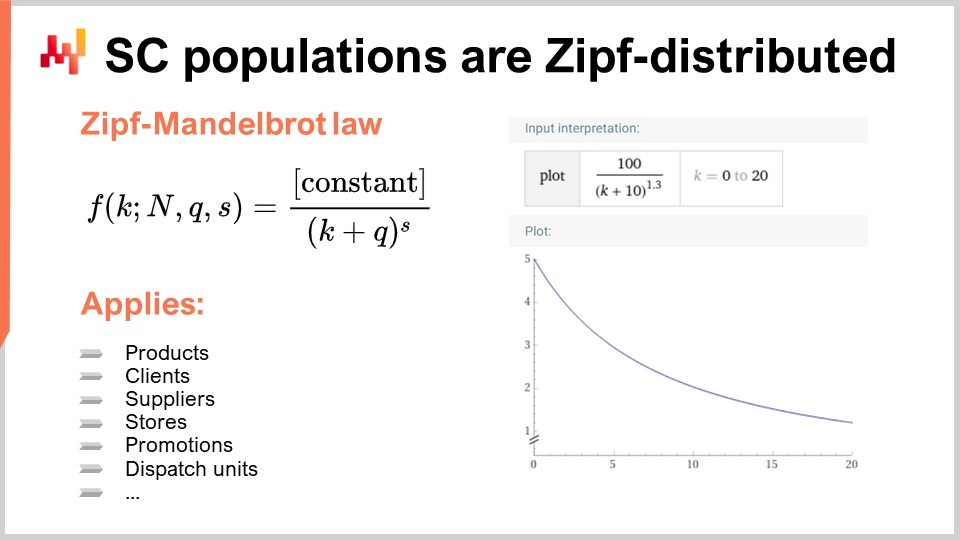
その代わり、サプライチェーンで興味深いほぼすべての分布はZipf分布に従います。Zipf分布は、示された数式で表現されます。この概念を理解するために、各製品の販売量という測定値に基づいて、製品群を考えてみてください。1年といった一定期間の中で、製品を販売量が多い順にランク付けします。そこで、ランクが与えられたときに予想される販売量を提供する曲線の形状を予測するモデルが存在するかどうかが問題となります。これがまさにZipf分布の本質です。ここで、fはZipf-Mandelbrot則の形状を表し、kはk番目に大きい要素を表します。正規分布における平均(μ)や分散(σ)のように、qとsという2つのパラメータが存在し、これらはデータから学習されます。これらのパラメータを用いて、対象となる集団に分布をフィッティングすることができます。Zipf-Mandelbrot則はこれらのパラメータを包含しています.
サプライチェーンにおけるほぼすべての対象集団がZipf分布に従っていることに留意することが重要です。これは、製品、クライアント、サプライヤー、プロモーション、さらには出荷ユニットに対しても当てはまります。Zipf分布は本質的にパレートの法則の派生形ですが、より扱いやすく、私の意見では、サプライチェーン上の任意の対象集団に期待されるものを明示的にモデル化しているため、より興味深いものです。もしZipf分布に従わない集団に出会った場合、それは原則からの真の逸脱というよりは、データに問題がある可能性が高いと言えるでしょう.

実世界でZipf分布の概念を活用するには、Envisionを使用できます。 このコードスニペットを見ると、実際のデータセットにこのモデルを適用するために数行のコードしか必要ないことがわかります。ここでは、数量を表す1列のデータを持つ「data.csv」というフラットファイルに、対象となる母集団が存在すると仮定しています。通常は、製品識別子と数量が存在します。4行目では、ランク集約器を用いて数量に基づいてランクを計算し並べ替えています。その後、6行目から11行目にかけて、Autodevによって明示的に示されたdifferentiable programmingブロックに入り、画面左側の数式と同様に、c、q、sという3つのスカラー・パラメータを宣言します。次に、Zipfモデルによる予測を計算し、観測された数量とモデルの予測との間の平均二乗誤差を用います。ごく数行のコードでZipf分布の回帰が可能になるのです。洗練されて聞こえても、適切なツールを使えば非常にシンプルです。

これにより、サプライチェーンのもう一つの観察的側面が明らかになります。サプライチェーンのどのレベルであっても、期待される数字は少なく、通常20未満です。観測されるデータ数が少ないだけでなく、観測される数字自体も小さいのです。もちろん、この原則は使用する単位に依存しますが、ここで「数字」と言うとき、サプライチェーンの観点から典型的な意味を持つ、すなわち観察して最適化しようとしているものを指しています。
小さな数字しか存在しない理由は、量的供給チェーンマニフェストに起因します。例として、店舗内のTシャツを考えてみましょう。店舗には何千枚ものTシャツが在庫としてあるかもしれませんが、実際にはサイズ、色、デザインにバリエーションのある何百種類ものTシャツが存在します。サプライチェーンの観点で重要な粒度、すなわちSKUでTシャツを見ると、あるSKUに対して数千枚のTシャツが存在するわけではなく、ほんの一握りしかないのです。
大量のTシャツがあったとしても、数千枚のTシャツがそのまま転がっていることはあり得ません。処理や移動の面で大問題になるからです。代わりに、それらのTシャツは便利な箱に梱包され、実際の運用ではそのように処理されます。例えば、Tシャツを大量に取り扱う流通センターでは、店舗に出荷するためにTシャツが箱に詰められているでしょう。場合によっては、サイズや色が異なるTシャツがフルアソートされた箱に入っており、チェーン全体の処理を容易にしているかもしれません。たとえ多数の箱が存在したとしても、数千個の箱がそのまま存在するわけではなく、数十個の箱であればきちんとパレットに整理されます。1つのパレットに数十個の箱が収まることができ、多くのパレットがある場合でも、それらが個々のパレットとしてばらばらに配置されるのではなく、通常はコンテナとして組織されます。そして、もし多くのコンテナがあれば、貨物船などが使用されるでしょう。
私が言いたいのは、サプライチェーンにおけるいかなる数字も、本質的には常に小さな数字であるということです。この状況は、単に上位の集約レベルに移るだけでは回避できません。なぜなら、集約レベルを上げると、規模の経済が働き、運用コストを下げるためにバッチ処理が導入されるからです。これは何度も繰り返され、最終的には店舗で販売される単品商品であっても、大量生産品であっても、常に小さな数字のゲームになるのです。
たとえ何百万枚ものTシャツを生産する工場があったとしても、おそらく巨大なバッチで生産され、その際に重要なのはTシャツの個数ではなく、バッチの数であり、これはずっと小さな数字になります。
ここで言いたいのは、まず科学計算や統計学で用いられるほとんどの手法を見渡す必要があるということです。サプライチェーンに関連しない他の多くの分野では、逆に、観測数が多く、精密さが求められる大きな数字が主流です。しかしサプライチェーンでは、観測される数字は小さく、かつ離散的なのです。
私の提案は、この原則に基づいたツールが必要であるということです。つまり、私たちが大きな数字ではなく、小さな数字に直面するという現実を十分に考慮し、取り入れたツールが必要だということです。もし、大数の法則、すなわち多数の観測や大きな数字そのものだけを前提に設計されたツールしか使えなければ、サプライチェーンでは全くのミスマッチとなります。
ちなみに、これはソフトウェアにも深い影響を与えます。小さな数字しかない場合、ソフトウェア層がこの観察結果を活かす手法は多く存在します。例えば、ハイパーマーケットの取引明細のデータセットを見てみると、私の経験と観察から、行の80%がハイパーマーケットで最終顧客に販売される数量が正確に1であることに気づくでしょう。では、この情報を表現するのに64ビットもの情報が必要でしょうか?いいえ、それはスペースと処理時間の大きな無駄です。この概念を取り入れることで、1桁または2桁のオーダーで運用効率を向上させることができます。これは単なる妄想ではなく、実際の運用上の利益につながるのです。現代のコンピュータは非常に強力ですが、その処理能力を、小さな数字が支配するサプライチェーン環境において、大きな数字を前提としたパラダイムのために無駄にしてしまうのはもったいないのです。
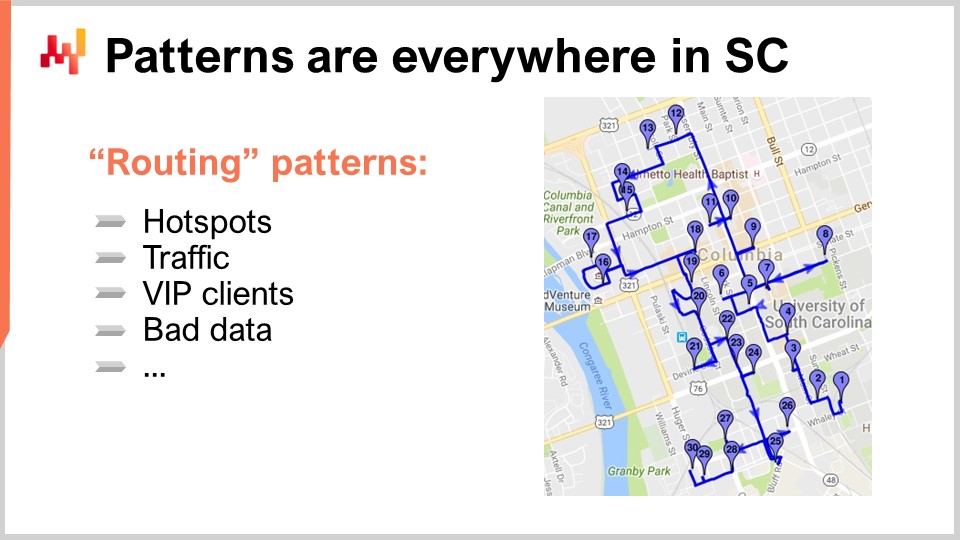
ここで、本日の最後の観察原則について触れます。サプライチェーンでは、あらゆるところにパターンが存在します。これを理解するために、通常パターンが存在しないと考えられている古典的なサプライチェーンの問題、すなわちルート最適化の問題を例にとってみましょう。ルート最適化の古典的な問題は、配達先リストが与えられた状態で、地図上に配置された配送先を通り、総輸送時間を最小限に抑える経路を見つけるというものです。一見すると、これはパターンを伴わない、純粋に幾何学的な問題のように思えます。
しかし、私はこの見方が完全に間違っていると主張します。この角度で問題に取り組むと、あなたは単に数学的な問題を扱っているに過ぎず、本来のサプライチェーンの問題を見失ってしまうのです。サプライチェーンは反復的なゲームであり、問題が何度も現れるのです。もし配送業務を行っているなら、ほぼ毎日配送を実施しているはずです。一つのルートだけではなく、文字通り毎日1つのルート、少なくともそれくらいは存在するはずです。
さらに、配送業務に従事している場合、複数の車両と運転手からなるフリートを持っている可能性が高いです。問題は単一のルートの最適化だけに留まらず、全フリートの最適化であり、このゲームは毎日繰り返されるのです。そこで、あらゆるパターンが現れるのです。
最初に、地図上のポイントはランダムに配置されているわけではありません。ホットスポット、つまり配送密度の高い地域があります。大都市にある大企業の本社のように、ほぼ毎日配送を受ける住所も存在します。大規模なeコマース企業であれば、この住所に毎営業日パッケージを配送しているはずです。これらのホットスポットは不変ではなく、季節性があります。夏や冬に非常に静かな地域もあります。パターンが存在しており、ルート最適化のゲームで非常に優れた結果を出すには、これらのホットスポットがいつどこで発生するかだけでなく、年間を通じてどのように移動するかも考慮する必要があります。さらに、交通状況も考慮に入れなければなりません。交通は時間依存であるため、幾何学的な距離だけを考えてはいけません。運転手が一日のある時点で出発すると、その後ルートを進むにつれて交通状況は変化します。このゲームをうまくプレイするためには、変動し予測可能な交通パターンを考慮する必要があります。たとえば、パリでは午前9時と午後6時に市全体が完全に渋滞しており、予測の専門家でなくともそれは明らかです。
また、現場で起こる出来事、例えば通常の交通パターンを乱す事故なども存在します。数学的な観点から配送を考えると、すべての配送ポイントが同一であると仮定しますが、実際はそうではありません。VIPクライアントがいたり、全体の半分を配送しなければならない特定の住所があったりします。効果的なルート最適化のためには、これらの重要な節目を考慮に入れる必要があります。
また、状況を把握する必要があり、世界に関するデータが不完全であることはよくあります。たとえば、橋が閉鎖されているにもかかわらずソフトウェアがそれを認識していない場合、問題は最初に橋が閉ざされていることを知らなかったのではなく、ソフトウェアがその問題から学ばず、常に最適とされるルートを提案するものの、結果として意味不明なルートになってしまう点にあります。その結果、人々はシステムに対抗することになり、サプライチェーンの観点からは実用的なルート最適化の解決策とは言えません。
要点は、サプライチェーンの状況を見ると、いたるところにパターンが存在するということです。洗練された数学的構造に気を取られず、これらの考察が時系列予測にも適用されることを忘れてはなりません。今回は、ルート最適化の問題がより顕在化していたため例として取り上げました。
結論として、サプライチェーンは明らかに見える次元や洗練された解だけでなく、観察可能なすべての次元から観察する必要があります。

これにより、サプライチェーンを見るべき方法に関連する第2の原則群に話が移ります。これまで、サプライチェーンを観察するための4つの原則、すなわち間接観察、エンタープライズソフトウェア、混乱の中から関連性のあるものとそうでないものを見極めること、そしてエントロピーに注目してきました。分布はしばしばZipfの法則に従い、少数でもパターンが現れることを観察しています。では、実際にどのように行動するのでしょうか?数学的な観点から言えば、最善の行動方針を決定するために何らかの最適化を行います。これが定量的な視点です。

まず注目すべきは、サプライチェーン向けの最適化ロジックが本番環境で稼働し始めると、バグなどの問題が発生するという点です。エンタープライズソフトウェアは非常に複雑で、多くの場合バグだらけです。自らサプライチェーン用の最適化ロジックを構築する際には、数多くの問題に直面するでしょう。しかし、あるロジックが本番投入されるほど十分であれば、現在直面している問題はおそらくエッジケースに過ぎません。もしエッジケースでなく、ソフトウェアやロジックが毎回誤作動していたならば、本番環境に投入されることはなかったでしょう。
この原則の考え方は、どんな問題も解決するのに5回から10回の反復が必要だということです。5~10回の反復と言うのは、問題に直面し、その原因を調査し、根本原因を理解して修正を試みるということを意味します。しかし、ほとんどの場合、その修正策だけでは問題は解決しません。問題の内部に隠れた別の問題が存在することや、自分が解決したと思っていた問題が実際の原因ではなかったこと、さらには状況がより広範な問題群を明らかにすることが分かるでしょう。あなたは広範な問題群の一部を解決したかもしれませんが、その問題の変種として別の問題が引き続き発生するのです。
サプライチェーンは複雑で絶えず変化する実世界のシステムであるため、すべての状況に対して完全に正しい設計を行うのは困難です。ほとんどの場合、最善を尽くして問題を解決し、その後、改良したロジックを実際の運用でテストして、機能するかどうかを確かめなければなりません。問題解決には反復が必要です。問題の解決に5〜10回の反復が必要であるという原則は、適応の速度やサプライチェーン最適化ロジックの更新・再計算頻度に大きな影響を与えます。たとえば、次の2年間の四半期予測を行うロジックがあり、それを四半期に一度しか実行しない場合、この予測ロジックに関する問題を解決するまでに1年から2年かかることになり、これは非常に長い時間です。
たとえ月ごとに実行されるロジック、例えばS&OP(セールス・アンド・オペレーションズ・プランニング)のプロセスであっても、問題を解決するには最長で1年かかる可能性があります。だからこそ、サプライチェーン最適化ロジックの実行頻度を上げることが重要なのです。たとえば、Lokadでは、5年先の予測であっても、すべてのロジックが毎日実行されています。これらの予測は、前日と大きく変わらなくても毎日更新されます。目的は統計的な精度を向上させることではなく、合理的な時間内に問題やバグを修正できるよう、ロジックを十分な頻度で実行することにあります。
この観察は、サプライチェーンマネジメントに固有のものではありません。Netflixのような企業の優れたエンジニアリングチームは、カオスエンジニアリングの概念を普及させました。彼らはエッジケースが稀であり、これらの問題を解決する唯一の方法は経験をより頻繁に繰り返すことだと認識しました。その結果、Chaos Monkeyと呼ばれるソフトウェアを作り、ネットワークの混乱やランダムなクラッシュを引き起こすことで、ソフトウェアインフラに混沌をもたらしています。Chaos Monkeyの目的は、エッジケースをより早く顕在化させ、エンジニアリングチームが迅速に対処できるようにすることです。
一見すると、オペレーションにさらなる混沌を導入するのは逆効果のように思えるかもしれませんが、このアプローチは高い信頼性で知られるNetflixにおいて有効であることが証明されています。彼らは、ソフトウェア起因の問題に直面した場合、解決までに多くの反復が必要であり、問題の核心に迫るためには迅速な反復が不可欠であることを理解しています。Chaos Monkeyは、反復速度を上げるための一つの方法にすぎません。
サプライチェーンの観点から見ると、カオスモンキーは直接適用できないかもしれませんが、サプライチェーン最適化ロジックの実行頻度を高めるという考え方は依然として非常に重要です。どのようなロジックであっても、それは高速かつ高頻度で実行されなければなりません。そうでなければ、直面する問題を一つも解決できないでしょう。

さて、長期間稼働しているサプライチェーンは準最適状態にあると言えます。ここでいう「長期間」とは、20年以上の運用実績があるサプライチェーンのことです。別の言い方をすれば、あなたのサプライチェーンの先人たちが全く無能だったわけではない、ということです。サプライチェーン最適化の取り組みを見ると、在庫レベルを半減させたり、サービスレベルを95%から99%に引き上げたり、ストックアウトを完全に無くしたり、リードタイムを半分にするなど、壮大な目標が掲げられることが多いです。これらは、ひとつのKPIに注目して大幅な改善を試みる一方向的な動きです。しかし、これらの取り組みは、何十年も運用されてきたサプライチェーンには、通常、そこに潜在する知恵があるという非常に単純な理由から、ほぼ必ず失敗しています。
例えば、サービスレベルが95%の場合、それを99%に引き上げようとすると、在庫レベルが大幅に増加し、その過程で大量の不要在庫が発生する可能性が高いです。同様に、一定の在庫量がある状態でそれを半分に削減する大規模な取り組みを行うと、持続不可能なサービス品質の問題が生じる可能性が高いです。
私が観察したところ、長期間運用されているサプライチェーンが一方向に準最適であるという原則を理解していない多くの実務者は、局所最適解の周辺で振動する傾向にあります。ここで、長期運用されているサプライチェーンが完全に最適であるとは言っていませんが、一方向に準最適であるというのです。グランドキャニオンの例えをすると、川は重力という一方向の力によって最適な流路を掘り進めます。たとえその力が10倍になったとしても、川は依然として多くの曲がりくねった道を描くでしょう。
要点は、長期間運用されているサプライチェーンで大幅な改善を図るには、複数の変数を同時に調整する必要があるということです。たった一つの変数にのみ注目しても、望む結果は得られません。特に、貴社が数十年にわたって現状維持で運用してきた場合、先人たちはその時代においていくつか正しい判断をしていたはずですから、誰も気に留めなかった極端に機能不全なサプライチェーンに偶然出会う可能性は極めて低いのです。サプライチェーンは厄介な問題であり、たとえ大規模に完全な機能不全状態を人工的に作り出すことが可能であっても、それは非常に稀なケースに過ぎません。

もう一つ考慮すべき点は、局所最適化は問題そのものを解決するのではなく、単に問題を先送りにするだけであるということです。これを理解するには、サプライチェーンが一つのシステムであり、サプライチェーンパフォーマンステストの観点からは、システム全体のパフォーマンスのみが重要だと認識する必要があります。局所的なパフォーマンスも重要ですが、全体像の一部に過ぎません。
一般的な考え方として、問題全般(サプライチェーンに限らず)に対して分割統治戦略を適用できるというものがあります。例えば、多くの店舗を持つ小売ネットワークでは、各店舗の在庫レベルを最適化したいと考えるかもしれません。しかし、実際には、店舗とそれらにサービスを提供する配送センターのネットワークがある場合、一店舗だけを微細に最適化して、その店舗だけ優れたサービスを実現しても、他の店舗に悪影響を及ぼすのは明白なのです。
正しい視点は、配送センターに1単位の在庫があるとき、まず自問すべきは「この単位はどこで最も必要とされているか?私にとって最も利益のある動きは何か?」ということです。在庫の配送、すなわち在庫管理定義の問題は、店舗レベルではなくシステム全体で考えるべき問題です。もし一店舗だけを最適化しようとすれば、他店舗で問題を引き起こす可能性が高いのです。
「局所的」という場合、この原則は単に地理的な意味だけでなく、サプライチェーン内の純粋な論理的な問題としても理解されるべきです。例えば、多くの製品カテゴリを持つeコマース企業では、各カテゴリごとに異なる予算を割り当てたいと考えるかもしれません。これもまた一種の分割統治戦略です。しかし、予算を各カテゴリに年初に固定的に分割して割り当てた場合、一方のカテゴリの需要が倍増し、他方のカテゴリの需要が半減したらどうなるでしょうか?この場合、二つのカテゴリ間で資金の不適切な配分という問題が生じます。ここでの問題は、いかなる分割統治の論理も適用できないという点にあります。局所最適化の技術を用いると、いわゆる最適化された解を作り出す過程で、かえって問題が新たに生まれてしまうかもしれません。

ここで、今日ご紹介した原則の中でもおそらく最も扱いにくい最後の原則に移ります。それは、「より良い問題設定はより良い解決策に勝る」というものです。これは特に一部の学術界で非常に混乱を招く考え方です。典型的な古典教育では、明確に定義された問題が提示され、次にその問題に対する解決策を探し始めます。例えば数学の問題では、ある生徒がより簡潔でエレガントな解答を提示し、それが最良の解答とされるのです。
しかし、実際のサプライチェーン管理では、物事はそのようには進みません。説明のために、60年前に遡って、非常に時間のかかる調理の問題を考えてみましょう。かつては、将来的にロボットが調理作業を担い、調理担当者の生産性を大幅に向上させるだろうと想像されていました。こうした考え方は1950年代、1960年代に広く信じられていました。
ところが、今日になって明らかになったのは、状況がそのように進化していないという事実です。調理の手間を最小限にするために、人々は今や既製の食事を購入するようになりました。これはまた、問題の転嫁の一例です。既製食事をスーパーマーケットに供給することは、参照商品数の増加や賞味期限の短縮といった理由で、生の製品を供給するよりもサプライチェーン上で困難なのです。この問題は、より優れたサプライチェーンの解決策によって解決されたのであって、より良い調理解決策が提供されたわけではありません。調理の問題は完全に取り除かれ、最小限の労力でまずまずの食事を提供するという新たな問題に再定義されたのです。
サプライチェーンの分野では、学術的な視点が既存の問題に対するより良い解決策の模索に偏りがちです。良い例としては、Kaggleコンペティションがあります。そこでは、データセット、問題、そして何百、何千ものチームが出揃い、最高の予測を目指して競い合うのです。明確に定義された問題と、数千もの解決策が互いに競う状況が存在します。この考え方の問題点は、サプライチェーンを改善するためには、より良い解決策が必要だという印象を与えてしまうことにあります。
この原則の本質は、より良い解決策がわずかな改善をもたらすかもしれないが、それはごく僅かなものでしかないということです。真に役立つのは、問題を再定義することであり、それは驚くほど困難な作業です。これは定量的な問題にも当てはまり、実際のサプライチェーン戦略と最適化すべき主要な問題について再考する必要があるのです。
多くの分野で、人々は問題を静的で不変なものとして捉え、より良い解決策を求めがちです。確かに、より優れた時系列予測アルゴリズムが役立つことは否定しませんが、時系列予測は統計的予測の領域に属し、サプライチェーン管理の全体最適とは別の領域の話です。旅行用スーツケースの例に戻ると、車輪付きスーツケースにおける重要な改善点は車輪そのものではなく、取っ手にあったのです。一見すると車輪と無関係に見えるこの改善点こそが、解決策の発見に40年を要した理由なのです。すなわち、より良い問題が浮かび上がるためには、既存の枠組みを超えた発想が求められるということです。
この定量的な原則は、直面する問題に挑戦することの重要性を説いています。もしかすると、あなたは問題について十分に考えておらず、解決策に執着してしまっているかもしれません。しかし、本来注目すべきは問題そのものと、その理解しきれていない部分です。問題が明確に定義された時点で、良い解決策は単なる実行の問題となり、さほど困難なものではなくなるのです。

結論として、サプライチェーンという学問分野には、印象的で権威ある多くの視点が存在します。これらは洗練されているかもしれませんが、ここで皆さんに問いかけたいのは、もしかするとそれらすべてが大きく誤った方向に進んでいるのではないか、ということです。時系列予測やオペレーショナルリサーチといった要素が問題に対する適切な視点であると本当に確信しているのでしょうか?どれだけの洗練さや、何十年にも及ぶエンジニアリングと努力が注がれても、私たちは本当に正しい道を歩んでいるのでしょうか?
本日、サプライチェーン管理にとって極めて重要であると私が考える一連の原則を紹介します。しかし、これらは皆さんの多くにとって奇妙に映るかもしれません。実績のあるものと奇妙なもの、二つの世界が存在する中で、数十年後に何が起こるのかが問われているのです。

進歩は混沌とした非線形のプロセスで展開する傾向があります。これらの原則の狙いは、予期せぬ事態に対応可能な、非常に混沌とした世界を受け入れることにあります。これにより、定量的な視点からサプライチェーンに改善をもたらす、より迅速で信頼性が高く、効率的なソリューションの開発が促進されるのです。

さて、いくつかの質問に移りましょう。
質問: ジップ分布はパレートの法則とどのように比較されるのでしょうか?
パレートの法則は80-20の経験則ですが、定量的な観点から見ると、ジップ分布は明示的な予測モデルです。その予測能力は、データセットに対して非常に直接的に検証することが可能です。
質問: ジップ・マンデルブロ分布は、疫学者が症例や死亡数を報告する際に用いる対数曲線として、サプライチェーンの変動を把握するために見る方が適切ではないでしょうか?
まったくその通りです。哲学的なレベルで言えば、あなたが生きるのは平凡の世界(Mediocrity-land)か、極端の世界(Extreme-land)かという問題です。サプライチェーンやほとんどの人間活動は極端な状況下に存在します。プロモーションの振幅を視覚化したい場合、対数曲線は実際に有用です。例えば、過去10年間の大規模小売ネットワークにおけるすべてのプロモーションの振幅を見ようとすると、通常スケールでは最大のプロモーションが他と比べ圧倒的に大きいため、他の数値が見えなくなってしまうかもしれません。したがって、対数スケールを用いれば変動がより明確に把握できるのです。ジップ・マンデルブロ分布を用いることで、数行のコードで展開できるモデルを提供しており、これは単なる対数的なデータの見方以上のものです。ただし、基本的な直感は同じだと私は考えます。高次の哲学的視点を求めるなら、ナシーム・タレブの『Antifragile』におけるMediocristan対Extremistanの概念を読むことをお勧めします。
質問: 局所的なサプライチェーン最適化に関して、サプライチェーンネットワークの協働やSNLPを支える基礎データに関連しているのでしょうか?
私が局所最適化に対して問題を感じるのは、大規模なサプライチェーンを運営する企業は通常、マトリックス組織を採用しているからです。この組織構造は分割統治的な考え方に基づいており、結果として局所的な最適化を意図的に促進してしまいます。例えば、需要予測を担当するチームと購買決定を担当するチームという、二つの異なるチームを考えてみてください。これらの問題、すなわち需要予測と購買最適化は完全に絡み合っており、需要予測の誤差率だけに注目して局所的に最適化し、その後で処理効率に基づいて購買を別々に最適化することはできません。システム全体への影響を考慮しなければならないのです。
今日、主要なサプライチェーンを推進する大企業が直面している最大の課題は、定量的な最適化を目指す際にシステム全体、ひいては会社全体を考える必要があるということです。これは、企業内で何十年にもわたって定着してきたマトリックス組織の枠組み、つまり各自が自分の明確な境界にのみ注目し大局を見失ってしまうという現状に反するものです。
この問題のもう一つの例は店舗の在庫です。在庫は、顧客の需要を満たすという役割と、商品としての役割の二つを持ちます。適正な在庫量を維持するためには、サービスの品質と店舗の魅力という両方の問題に取り組む必要があります。店舗の魅力とは、顧客に対して店舗を魅力的かつ興味深く見せることであり、これはマーケティングの問題に近いのです。企業内にはマーケティング部門とサプライチェーン部門がありますが、サプライチェーン最適化に関しては自然な協働が行われるわけではありません。つまり、これらすべての側面を統合しなければ、最適化は機能しないのです。
SNLPに関するあなたの懸念については、人々が単に会議のためだけに集まるという非効率な状況が問題です。数ヶ月前にSNLPに関するLokad TVのエピソードを公開していますので、具体的な議論をご希望であればそちらを参照してください。
質問: サプライチェーン戦略と定量的な実行の間で、時間とエネルギーはどのように配分すべきでしょうか?
素晴らしい質問です。私が第2回目の講義で述べたように、その答えは、日常業務の完全なロボット化が必要だということです。これにより、数値的な施策の継続的な戦略的改善に全ての時間とエネルギーを注ぐことが可能になります。もしサプライチェーン実行の些細な業務に10%以上の時間を割いているのであれば、その方法論自体に問題があると言えるでしょう。サプライチェーンの専門家は、本来自動化されるべき些細な実行問題に時間とエネルギーを浪費するほど貴重な存在ではありません。
戦略的な思考にほぼ全エネルギーを注げる方法論を採用する必要があり、その結果、即座に卓越した数値レシピとして実装され、日々のサプライチェーン運用を推進します。これは、ソフトウェア製品志向のデリバリーについて語る私の第三回目の講義に関連しています。
質問: 体系的な定式化に基づいたサプライチェーン問題に対し、最高の改善が可能な一種の天井分析を仮定することはできるのでしょうか?
私は決してそれは可能ではないと言いたいです。最適解や天井が存在すると考えることは、人間の創意工夫にも限界があると主張するのと同じです。人間の創意工夫に限界がないという証拠はありませんが、これは私の根本的な信念の一つです。サプライチェーンは厄介な問題です。問題を変革し、場合によっては大きな問題を企業にとっての大きな解決策や成長の機会へと変えることができます。たとえば、Amazonを見てください。2000年代初頭、ジェフ・ベゾスは、小売業者として成功するためには巨大で堅牢なソフトウェア基盤が必要であると理解しました。しかし、Amazonの電子商取引を運営するために必要なこの大規模で産業用の生産グレードのインフラは信じられないほど高価で、企業に数十億ドルもの費用がかかりました。そこで、Amazonのチームは、この莫大なクラウドコンピューティングインフラを、非常に大きな投資であったにもかかわらず、商業製品へと転換することに決めたのです。今日では、この大規模なコンピューティングインフラは、実際にAmazonの主要な利益源の一つとなっています。
厄介な問題について考え始めると、常に問題をより優れた形で再定義できることが理解できます。だからこそ、最適解が存在すると信じるのは誤りだと思うのです。天井分析の観点から考えると、固定された問題を対象としており、その固定された問題に対してはおそらく準最適な解決策が存在するかもしれません。たとえば、現代のスーツケースの車輪はおそらく準最適と言えるでしょう。しかし、完全に自明であるはずの何かを見落としてはいないでしょうか? もしかすると、車輪をはるかに改良する方法、これまで発明されていなかった革新が存在するかもしれません。それが現れたとたん、完全に自明な解決策に思えることでしょう。
だからこそ、これらの問題には天井がないと考える必要があります。問題は恣意的なものであり、問題を再定義して全く異なるルールでゲームを行うことができるのです。これは、人々がきちんとデザインされた問題を持ち、それに対して解決策を見出せると考える傾向があるため、両義的なものになっています。現代の西洋教育システムは、問題を提示してその解決策の質を評価するという、解決策発見型のマインドセットを強調します。しかし、本当に興味深いのは、問題そのものの質なのです。
質問: 最良の解決策は問題を解決するものですが、時には最良の解決策を見出すために時間とお金の両方がかかることがあります。これに対して何か回避策はあるのでしょうか?
もちろんです。理論上は正しい解決策であっても、実行に非常に時間がかかるのであれば、それは良い解決策とは言えません。この種の考えは、実際の世界と無関係な狭い数学的基準に基づいて完璧な解決策を追求する、特定の学術界で見られる傾向です。これこそが、私が適切な最適化問題について言及した際に話していたことなのです。
四半期ごとに、一人の教授が私のもとを訪れて、ルート最適化問題を解くためのオンラインアルゴリズムのレビューをしてほしいと頼むのです。最近私がレビューする論文のほとんどはオンライン版に焦点を当てています。私の返答はいつも同じです。あなたは正しい問題を解いていない。私にはあなたの解決策に興味はありません。なぜなら、あなたはそもそも問題そのものについて正しく考えていないからです。
進歩は洗練と混同してはなりません。進歩が単純なものから洗練されたものへと変化するという誤った認識は危惧すべきものです。実際には、進歩はしばしば極めて複雑なものから出発し、優れた思考と技術によってシンプルな形態へと到達することで実現されます。たとえば、21世紀のサプライチェーン動向に関する私の最後の講義では、ヴェルサイユ宮殿へ水を供給したマリーの機械が紹介されました。それは非常に複雑なシステムでしたが、現代の電動ポンプははるかにシンプルで効率的です。
進歩は必ずしも余分な洗練の中に見出されるものではありません。必要な場合もありますが、それが進歩の不可欠な要素というわけではありません。
質問: 大規模な小売ネットワークは在庫水準を主導していますが、注文をほぼ即座に履行する必要があります。時には、サプライヤー側からではなく自社でプロモーションを行うこともあります。このような場合、サプライヤー側でどのように予測し、それに応じた準備をすればよいのでしょうか?
まず、私たちは問題を異なる視点から見なければなりません。あなたは、何の前触れもなく大規模なプロモーションを展開する大手小売業者という、予測に基づく視点を前提としています。しかし、まずそれは必ずしも悪いことなのでしょうか? あなたの商品が事前の通知なしにプロモーションされたとしても、それはただの現実の一部に過ぎません。過去の履歴を見ると、そのような事象は定期的に発生しており、パターンすら存在しています。
私の原則に立ち返れば、パターンは至る所にあります。まず、未来を予測するのではなく、確率的予測を採用すべきだという視点を持つ必要があります。たとえ変動を完全に予期できなくても、それが全く予想外であるとも限らないのです。もしかすると、完全にサプライヤーに驚かされるのではなく、ゲームのルール自体を変える必要があるのかもしれません。もしくは、小売業者、小売ネットワーク、サプライヤーを拘束するようなコミットメントを交渉する必要があるかもしれません。もし小売ネットワークがサプライヤーに前もって知らせることなく大々的なプロモーションを始めた場合、現実的にはサプライヤーがサービス品質の維持に対して責任を負うことはできないのです。
もしかすると、解決策はもっと協力的なものかもしれません。サプライヤーはより優れたリスク評価を行うべきでしょう。もしサプライヤーが扱う資材が劣化しやすいものでなければ、数ヶ月分の在庫を持つことでより利益が出る場合もあります。人々はしばしば、遅延ゼロ、在庫ゼロ、全てゼロを理想と考えますが、果たしてそれが顧客の期待するものなのでしょうか? 顧客が求めているのは、豊富な在庫という付加価値かもしれません。繰り返しになりますが、答えは様々な要因に依存します。
問題を多角的に捉える必要があり、簡単な解決策は存在しません。直面している問題について真剣に考え、利用可能なすべての選択肢を検討すべきです。もしかすると、問題は在庫の量ではなく、生産能力そのものにあるのかもしれません。もし需要が急増し、大きなスパイクが発生するのに過度な費用がかからず、サプライヤーのサプライヤーが資材を迅速に提供できるのであれば、必要なのはより柔軟な生産能力にすぎないかもしれません。これにより、急増している商品に生産能力を振り向けることが可能になるのです。
ちなみに、これは特定の産業では実際に存在します。例えば、パッケージング業界は大規模な生産能力を保有しています。パッケージング業界のほとんどの機械は産業用プリンターであり、比較的安価です。この業界の人々は通常、ほとんど使用されない多くのプリンターを所有しています。しかし、大きなイベントがあったり、有名なブランドが大々的なプロモーションを行う場合には、新たなマーケティングの推進に合わせた大量の新パッケージを印刷する能力を持っているのです。
したがって、状況は様々な要因に依存するため、明確な答えを持っていないことをお詫び申し上げます。しかし、確実に言えるのは、直面している問題について真剣に考える必要があるということです。
これにて本日の講義、序章の第6回目かつ最後の講義を終了します。2週間後、同じ曜日、同じ時刻にサプライチェーンのパーソナリティについて講演いたします。それでは、また次回お会いしましょう。


