00:01 はじめに
02:44 予測ニーズの調査
05:57 モデルとモデリングの違い
12:26 これまでの経緯
15:50 少し理論と少し実践
17:41 微分可能プログラミング、SGD 1/6
24:56 微分可能プログラミング、自動微分 2/6
31:07 微分可能プログラミング、関数 3/6
35:35 微分可能プログラミング、メタパラメータ 4/6
37:59 微分可能プログラミング、パラメータ 5/6
40:55 微分可能プログラミング、癖 6/6
43:41 ウォークスルー、小売需要予測
45:49 ウォークスルー、パラメータフィッティング 1/6
53:14 ウォークスルー、パラメータ共有 2/6
01:04:16 ウォークスルー、損失マスキング 3/6
01:09:34 ウォークスルー、共変量統合 4/6
01:14:09 ウォークスルー、スパース分解 5/6
01:21:17 ウォークスルー、フリースケーリング 6/6
01:25:14 ホワイトボックス化
01:33:22 実験的最適化に戻る
01:39:53 結論
01:44:40 次回の講義と聴衆からの質問
説明
Differentiable Programming (DP) は、幅広い統計モデルの設計に利用される生成的パラダイムであり、予測的な供給チェーンの課題に非常に適しています。DPは、パラメトリックモデルに基づくほぼすべての「古典的」な予測手法を凌駕します。また、DPは実務者による採用の容易さを含む、サプライチェーン用途において重要なほぼ全ての側面で、2010年代後半までの「古典的な」機械学習アルゴリズムよりも優れています。
完全な書き起こし

このサプライチェーン講義シリーズへようこそ。私はジョアンネス・ヴェルモレルです。本日は「サプライチェーンにおける微分可能プログラミングを用いた構造化予測モデリング」をお届けします。正しい行動方針を選ぶには、未来に関する詳細な定量的洞察が必要です。実際、より多くの購入や生産など、あらゆる決定は未来へのある程度の予測を反映しています。主流のサプライチェーン理論は、この問題に取り組む手段として予測の概念を強調します。しかしながら、少なくとも古典的な形態において、予測の視点は二つの点で不足しています.
第一に、これは狭い時系列の予測視点に偏っており、現実のサプライチェーンに見られる多様な課題に対処するには不十分です。第二に、時系列の予測精度に狭い焦点を当てるため、本質を見失っているのです。僅かに予測精度が上がったとしても、それが自動的にサプライチェーンのリターン増加に結びつくわけではありません.
本講義の目的は、技術と手法の両面を併せ持つ、予測に対する代替アプローチを探求することにあります。ここでの技術は微分可能プログラミング、手法は構造化予測モデルとなります。本講義の終わりまでには、このアプローチをサプライチェーンの状況に適用できるようになるはずです。このアプローチは理論的なものではなく、ここ数年、Lokadにおける標準的なアプローチとなってきました。また、前回の講義をご覧になっていなくても、本講義が全く理解不能ということはありません。しかし、この講義シリーズでは、講義を順番に視聴することで大いに理解が深まる段階に達しています。本講義では、以前の講義で紹介された要素をいくつか再検討します.

サプライチェーンの予測ニーズを検討する際、将来の需要の予測が最も明白な候補となります。実際、需要をより正確に予測することは、より多くの購入や生産など、基本的な意思決定において不可欠な要素です。しかし、この講義シリーズの第三章で紹介したサプライチェーンの原則を通じて、サプライチェーンを推進するための予測要件には非常に多岐にわたる期待が存在することがわかりました.
特に、例えば、リードタイムは変動し、季節的なパターンを示します。ほぼすべての在庫に関する意思決定は、将来の需要だけでなく、将来のリードタイムの予測を必要とします。したがって、リードタイムは予測されなければなりません。返品は、フローの半分を占めることもあります。例えば、ドイツのファッション・イーコマースではそのような状況が見られます。そうした状況では、返品の予測が重要となり、製品ごとに返品の傾向が大きく異なります。したがって、その場合も返品は予測される必要があります.
供給面では、生産そのものが変動する可能性があり、それは単に追加の遅延やリードタイムの変動だけが原因ではありません。例えば、生産にはある程度の不確実性が伴うことがあります。これは農業のような低技術の分野で発生することもありますが、製薬業界のようなハイテク分野でも起こり得ます。したがって、生産収率も予測されなければなりません。最後に、顧客の行動も非常に重要です。例えば、獲得を促進する製品による需要喚起は非常に重要であり、逆に、ストックアウトが原因で大きな顧客離れを引き起こす製品の場合、その在庫切れが問題となります。したがって、そのような行動は分析・予測、つまり予測される必要があります。ここでの重要なポイントは、時系列予測はパズルの一部に過ぎないということです。現実のサプライチェーンが抱えるすべての状況に対応できるアプローチを持つためには、これらすべての状況を包含する予測的アプローチが必要不可欠です.

予測問題に関して一般的なアプローチは、モデルを提示することです。このアプローチは何十年にもわたり時系列予測の文献を牽引してきており、現在でも機械学習分野における主流のアプローチと言えるでしょう。私が「モデル中心的アプローチ」と呼ぶこの方法は非常に広範に浸透しており、そのモデル中心の視点が実際に何を意味しているのか、一度立ち止まって評価するのも難しいほどです.
本講義で私が提案するのは、サプライチェーンにはモデリング技術、すなわちモデリング中心の視点が必要であり、どれだけ多くのモデルを用いても現実のサプライチェーンが抱えるすべての要求に対応するには不十分であるということです。ここで、モデル中心的アプローチとモデリング中心的アプローチの違いを明確にしましょう.
モデル中心的アプローチは、何よりもまずモデルを重視します。モデルは一つのパッケージとして提示され、実行可能な数値レシピやソフトウェアの形を取ることが一般的です。たとえそのようなソフトウェアが存在しなくても、モデル自体が数学的に正確に記述され、完全な再実装が可能であることが期待されます。このパッケージ、すなわちソフトウェア化されたモデルが最終成果物と見なされるのです.
理想的には、このモデルはまるで数学的関数のように振る舞うことが期待されます。すなわち、入力があり、結果が出力されるのです。もしモデルに何らかの設定可能性が残されている場合、その設定項目は未解決の問題として扱われます。実際、すべての設定オプションはモデルの一貫性を弱めます。モデル中心的アプローチにおいて設定可能な要素やあまりにも多くのオプションが存在すると、モデルは複数のモデルへと分散し、結果として単一のモデルというものが存在しなくなり、ベンチマークが困難になってしまいます.
一方、モデリングアプローチは設定可能性に対して全く逆の観点を取ります。モデルの表現力を最大化することが最終目的となるのです。これは欠陥ではなく、むしろ特徴となります。モデリング中心の視点で提示される内容は一見混乱を招くかもしれません。なぜなら、モデリング中心のアプローチのプレゼンテーションでは、あくまで複数のモデルが示されるのですが、それらのモデルは全く異なる意図を持っているからです.
モデリングの視点から見ると、提示されるモデルはあくまで一例に過ぎません。それは完全なものや問題の最終的な解決策を示すものではなく、モデリング手法そのものを説明する一段階にすぎません。モデリング手法における主な課題は、アプローチの評価が非常に困難になる点です。実際、モデリング中心の視点では、モデルの可能性は広がるものの、単一のモデルに焦点を当てる単純なベンチマークが失われてしまいます。つまり、どちらか一方のモデルと比較するというよりも、私たちが持っているのは熟慮された意見ということになります.
しかしながら、ベンチマークがあり、その数値が示されているからといって自動的に科学的であるとは限らないことをすぐに指摘しておきたいと思います。その数値が単に無意味なものの場合もあれば、逆に熟考された意見だからといって科学性が劣るわけでもありません。つまり、単に異なるアプローチに過ぎず、現実にはさまざまなコミュニティ内でこの二つのアプローチは共存しているのです.
例えば、Facebookのチームが2017年に発表した論文 “Forecasting at Scale” では、ほぼモデル中心的アプローチの原型が提示されています。この論文ではFacebook Prophetモデルが紹介されています。一方、別のFacebookチームが2018年に発表した論文 “Tensor Comprehension” では、本質的にモデリング手法が示されています。この論文はモデリングアプローチの原型とみなすことができます。つまり、同じ企業内で同時期に活動する研究チームであっても、状況に応じて異なる角度から問題に取り組むことがあるのです.
本講義は一連のサプライチェーン講義の一部です。第一章では、サプライチェーンを学問としても実践としても捉える私の見解を示しました。初回の講義から、主流のサプライチェーン理論が期待に応えていないと主張してきました。実際、主流のサプライチェーン理論はモデル中心的アプローチに大きく依存しており、この点が現実のサプライチェーンの要求との間に摩擦を生む主な原因の一つであると考えています.
この講義シリーズの第二章では、一連の手法を紹介しました。実際、素朴な手法はサプライチェーンの状況が断続的かつしばしば対立的であるために通常は通用しません。特に、第二章の中にあった “Empirical Experimental Optimization” というタイトルの講義は、本講義で私が採用している視点と同様のものです.
第三章では、一連のサプライチェーンのペルソナを紹介しました。これらのペルソナは、候補となる解決策を一切考慮せず、私たちが直面する問題に専念することを意味しています。現実のサプライチェーンが抱える多様な予測課題を理解する上で、これらのペルソナは非常に有用です。これにより、現実のサプライチェーンの細部にほとんど注意が払われない狭い時系列の視点に囚われることを避けることができると考えています.
第四章では、一連の補助的な科学分野を紹介しました。これらの分野はサプライチェーンとは異なりますが、現代のサプライチェーン実務にはこれらの基礎知識が不可欠です。第四章では微分可能プログラミングの話題に軽く触れましたが、数分後にこのプログラミングパラダイムをより詳しく再紹介する予定です.
最後に、この第五章の最初の講義では、シンプルで、ある人は単純すぎると言うかもしれないモデルが、2020年に開催された世界規模の予測コンペティションで最先端の予測精度を達成するのを目の当たりにしました。本日は、前回の講義で紹介したこのモデルに関わるパラメータを学習するための一連の手法を紹介します.
本講義の残りは大きく二つのブロックに分かれ、その後にいくつかの締めの考察が続きます。第一のブロックは微分可能プログラミングに関するものです。第四章でこのトピックに触れましたが、今回はさらに詳しく見ていきます。本講義の終了時までには、ほぼ自身で微分可能プログラミングの実装を作成できるようになるはずです。ここで「ほぼ」と言うのは、使用している技術スタックによって進捗が異なる可能性があるためです。また、微分可能プログラミングは一筋縄ではいかない技術であり、実践でスムーズに動作させるにはある程度の経験が必要です.
本講義の第二のブロックは、小売需要予測の状況についてのウォークスルーです。このウォークスルーは、前回の講義で紹介した、2020年のM5予測コンペティションで1位を達成したモデルに続くものです。しかし、前回の講義ではモデルのパラメータがどのように計算されたのかについては詳述しませんでした。今回のウォークスルーではそれを詳細に解説し、前回触れなかったストックアウトやプロモーションなどの重要な要素についても取り上げます。最後に、これらの要素すべてに基づいて、サプライチェーン目的における微分可能プログラミングの適合性について私見を述べます.

確率的勾配降下法(SGD)は、微分可能なプログラミングの2本の柱の1つです。SGDは一見シンプルに見えますが、その効果がなぜ非常に高いのか完全には解明されていません。効果がある理由は絶対に明らかですが、なぜそれほど優れているのかがあまり明確ではありません。
確率的勾配降下法の歴史は1950年代にさかのぼることができ、かなり長い歴史を持っています。しかし、この手法が主流の認知を得たのは、ディープラーニングの出現したここ10年間のみです。確率的勾配降下法は数学的最適化の観点に深く根ざしています。我々は最小化したい損失関数Qを持ち、すべての可能な解を表す実数パラメータの集合Wを持っています。求めたいのは、損失関数Qを最小化するパラメータWの組み合わせです。
損失関数Qは基本的な特性を保持している必要があります:それは一連の項に加法的に分解可能であるということです。この加法分解の存在が確率的勾配降下法を機能させる根拠です。もし損失関数がこのように加法的に分解できない場合、確率的勾配降下法は有効な手法として適用できません。この観点では、Xは損失関数に寄与するすべての項の集合を表し、Qxは部分的損失を意味し、損失関数を部分項の和として捉える観点で各項の損失を表しています。
確率的勾配降下法は学習状況特有のものではありませんが、機械学習のユースケース全体に非常によく適しています。ここでいう学習とは、機械学習における学習を意味します。実際、トレーニングデータセットがある場合、このデータセットは観測値のリストの形となり、各観測はモデルの入力を表す特徴量と出力を表すラベルのペアで構成されます。本質的に、学習の視点からは、トレーニングデータセットに基づいて経験的誤差などにおいて最も良いパフォーマンスを示すモデルを設計することが求められます。学習の観点では、Xは実際にはその観測値のリストとなり、パラメータはこのデータセットに最も適合するように最適化する機械学習モデルのパラメータとなります。
確率的勾配降下法は基本的に、一度に1つの観測をランダムに選びながら反復処理を進める手法です。一度に1つの観測、すなわち小さなXを選び、その観測に対して、局所的な勾配(すなわちQxのnablaで表現される)を計算します。これは損失関数の全体ではなく、その一部分にのみ適用される局所的な勾配、つまり部分的な勾配と言えます。
確率的勾配降下法の1ステップは、この局所勾配を取り、部分的な観測に基づいてパラメータWを少しずつ更新することから成り立ちます。ここで実際に起こっているのは、WがW - η×nabla QxWとなって更新されるということです。これは、簡潔に言えば、学習の観点から1つの観測Xによって得られる局所勾配の方向にWパラメータを微調整することを意味し、その後ランダムに局所勾配を適用して反復していくのです。
直感的に、確率的勾配降下法が非常にうまく機能するのは、より高速な反復とノイズの多い勾配との間にトレードオフが存在するためです。確率的勾配降下法の本質は、勾配の測定が完璧でなくても、それを非常に高速に得られれば問題としない点にあります。たとえノイズの多い勾配であっても、より高速な反復が可能であれば、それを採用すべきです。これが、特定の解の品質を達成するために必要な計算資源を最小限に抑える上で、確率的勾配降下法が非常に効果的である理由です。
最後に、ηという変数があります。これは学習率と呼ばれます。実際には、学習率は定数ではなく、確率的勾配降下法の進行中に変動します。Lokadでは、学習率の進化を制御するためにAdamアルゴリズムを使用してηパラメータを調整しています。Adamは2014年に発表された手法で、確率的勾配降下法が関わる際には機械学習コミュニティで非常に人気があります。

微分可能なプログラミングの2本目の柱は自動微分です。この概念は既に前の講義で見たことがあるでしょう。ここで、コードの一部を通じてこの概念を再考してみましょう。このコードは、サプライチェーンの予測最適化の目的でLokadが設計したドメイン固有のプログラミング言語Envisionで書かれています。Envisionを選んだのは、他の言語(Python、Java、またはC#など)を使用する場合に比べ、例がはるかに簡潔で、かつ明確になることが期待できるからです。しかし、Envisionを使用しているからといって、何らかの秘伝のテクニックが組み込まれているわけではありません。これらの例は、他のプログラミング言語でも完全に再実装可能です。コード行数はおそらく10倍になるでしょうが、全体としては些細な違いに過ぎません。ここでは講義の一環として、Envisionが非常に明確かつ簡潔な説明を提供してくれています。
微分可能なプログラミングが線形回帰にどのように応用できるか見てみましょう。これは単なるおもちゃの問題であり、線形回帰に微分可能なプログラミング自体は必須ではありません。目的は単に、微分可能なプログラミングの構文に慣れることにあります。1行目から6行目では、観測テーブルを表すテーブルTを宣言しています。ここで言う観測テーブルとは、確率的勾配降下法で表されたXセットのことを指します。全く同じものです。このテーブルは、Xと表される特徴量の列とYと表されるラベルの列の2列から構成されています。求めたいのは、入力としてXを取り、線形モデル、より正確にはアフィンモデルによってYを予測することです。明らかに、このテーブルTには4つのデータポイントしか含まれていません。これは説明を明確にするための、非常に小さなデータセットです。
8行目では、autodiffブロックを導入しています。このautodiffブロックは、Envisionにおけるループと見なすことができます。今回の場合、このループはテーブルTを反復処理します。これらの反復は確率的勾配降下法のステップを反映しており、Envisionの実行がこのautodiffブロックに入ると、観測テーブルから1行ずつ選び、その後確率的勾配降下法のステップを適用する一連の繰り返し実行が行われます。そのため、勾配が必要となるのです。
勾配はどこから来るのでしょうか?ここでは、我々のモデルであるAx + Bという小さなプログラムを書いています。さらに損失関数として平均二乗誤差を導入し、勾配を求めます。このような単純な状況では、手動で勾配を記述することも可能ですが、自動微分という技術を用いると、プログラムを2通りの形にコンパイルできます。1つはプログラムの順方向実行用、もう1つはプログラムに含まれるすべてのパラメータに対する勾配を計算する逆方向実行用です。
9行目と10行目では、キーワード「auto」を使って2つのパラメータAとBを宣言しています。これは、Envisionにこれらのパラメータの値を自動で初期化するよう指示するものです。AとBはスカラー値です。自動微分はこのautodiffブロック内のすべてのプログラムに適用されます。本質的には、コンパイラレベルでこのプログラムを2回コンパイルする技術であり、一回は順方向パス用、もう一回は逆方向パス用で、後者は勾配の値を提供します。自動微分技術の素晴らしさは、通常のプログラムの実行に要するCPU量と逆方向パスで勾配を計算するためのCPU量がほぼ同等であることを保証する点にあります。これは非常に重要な特性です。最後に、14行目で、上記のautodiffブロックによって学習されたパラメータを出力しています。

微分可能なプログラミングは、そのプログラミングパラダイムとして真価を発揮します。任意の複雑なプログラムを構成し、そのプログラムの自動微分を実行することが可能です。このプログラムには、例えば分岐や関数呼び出しが含まれていても構いません。このコード例は、前回の講義で紹介したピンボール損失関数の定義を再考するものです。ピンボール損失関数は、経験的確率分布からの乖離が観測された際に、分位数推定値を導出するために使用されます。もし平均二乗誤差を最小化すれば、経験分布の平均の推定値が得られ、ピンボール損失関数を最小化すれば、分位数ターゲットの推定値が得られます。たとえば、90パーセンタイルを目標とするということは、対象の確率分布において、将来観測される値があなたの推定値以下である確率が90%(あるいは上回る確率が10%)であることを意味します。これはサプライチェーンにおけるサービスレベルの定義の分析を彷彿とさせます。
1行目と2行目では、ポアソン分布からランダムにサンプリングされた乖離値で埋められた観測テーブルを導入しています。ポアソン分布の値は平均3でサンプリングされ、10,000個の乖離値が得られます。4行目と5行目では、独自実装のピンボール損失関数を展開します。この実装は、前回の講義で紹介したコードとほぼ同一ですが、関数の宣言に「autodiff」というキーワードが追加されています。このキーワードが付加されることで、Envisionコンパイラはこの関数を自動的に微分できるようになります。理論上は、自動微分はどんなプログラムにも適用可能ですが、実際には微分が意味をなさないプログラムや関数も多々存在します。たとえば、2つのテキスト値を取り連結する関数では、自動微分を適用する意味はありません。自動微分は、入力と出力に数値が存在する関数でのみ意味を成します。
7行目から9行目では、autodiffブロックがあり、観測テーブルを通じて受け取った経験分布のターゲット分位数推定値を計算します。内部的には、これが実際にはポアソン分布です。分位数推定値は、8行目で「quantile」という名前のパラメータとして宣言され、9行目で独自実装のピンボール損失関数が呼び出されます。分位数ターゲットは0.5に設定されているため、実際には分布の中央値の推定値を求めています。最後に、11行目でautodiffブロックの実行を通じて学習された値を出力します。このコード例は、自動微分が関数呼び出しや分岐を含むプログラムにも完全に自動で適用できることを示しています。

autodiffブロックは、観測テーブルから一度に1行ずつ選び、確率的勾配降下法(SGD)の一連のステップを実行するループとして解釈できると述べました。しかし、この状況での停止条件については、まだあまり明示していません。Envisionにおいて、確率的勾配降下法はいつ停止するのでしょうか?デフォルトでは、確率的勾配降下法は10エポック後に停止します。機械学習用語でのエポックとは、観測テーブルを完全に一巡することを意味します。7行目では、autodiffブロックに「epochs」という属性を付与できます。この属性は省略可能で、デフォルトの値は10ですが、指定することで異なる回数を選べます。ここでは、100エポックを指定しています。計算の総時間はエポック数にほぼ線形であるため、もしエポック数が2倍になれば、計算時間もほぼ2倍になることに注意してください。
なお、7行目ではautodiffブロックに「learning_rate」という2番目の属性も導入されています。この属性も省略可能で、デフォルトは0.01です。学習率は、確率的勾配降下法のステップで見たηパラメータの進化を制御するAdamアルゴリズムの初期化に使われる係数です。これは基本的にあまり頻繁に触る必要のないパラメータですが、場合によってはこのパラメータを調整することで、全体の計算時間の約20%を節約できる可能性があります。

autodiffブロックで学習されるパラメータの初期化についても、さらに詳しく検討する必要があります。これまで「auto」というキーワードを使用してきましたが、Envisionではこれは、平均1、標準偏差0.1のガウス分布からランダムに値を抽出してパラメータを初期化することを意味します。この初期化方法は、通常ディープラーニングで行われる、ゼロを中心とするガウス分布によるランダム初期化とは異なります。Lokadがこの異なるアプローチを採用した理由は、後ほど実際の小売需要予測の状況に進む際に、より明確になるでしょう。
Envisionでは、パラメータの初期化を上書きして制御することが可能です。たとえばパラメータ “quantile” は9行目で宣言されていますが、初期化する必要はありません。実際、7行目では自動微分ブロックの直上に変数 “quantile” があり、値4.2が代入されているため、すでに特定の値で初期化されています。自動初期化はもはや不要です。パラメータに許容される値の範囲を強制することも可能で、これは9行目のキーワード “in” によって行われます。基本的に、“quantile” は1から10の間(両端を含む)であるべきと定義しています。これらの境界が設定されると、Adamアルゴリズムから得られる更新が許容範囲外にパラメータ値を押し出そうとした場合、その変化を制限して範囲内にとどめます。さらに、通常Adamアルゴリズムに付随するモーメンタム値もゼロに設定します。パラメータ境界の強制は従来のディープラーニングの方法とは異なりますが、この機能の利点は、実際の小売需要予測の例を議論し始めると明らかになるでしょう.

微分可能プログラミングは確率的勾配降下法に大きく依存しています。確率的要素こそが降下法を非常に高速に動作させる原動力であり、これは両刃の剣でもあります。部分的な損失から得られるノイズは単なる欠陥ではなく、特徴でもあります。少しのノイズがあれば、非常にフラットな勾配の領域に陥ることを避けることができるのです。つまり、ノイジーな勾配を持つことで、反復処理が速くなるだけでなく、勾配が極端に平坦になり降下が鈍る領域から抜け出す手助けにもなります。しかし、確率的勾配降下法使用時には、勾配の総和が和の勾配と同じでないことに注意が必要です。そのため、特に裾分布に関しては、わずかな統計的バイアスが生じます。それでも、こうした懸念がある場合は、理論がやや不透明でも数値的な手法で対応することは比較的簡単です.
微分可能プログラミング(DP)を、任意の数学的最適化ソルバーと混同してはなりません。微分可能プログラミングが機能するためには、勾配がプログラム全体を通じて流れる必要があります。微分可能プログラミングは任意に複雑なプログラムでも動作しますが、そのプログラムは微分可能プログラミングを念頭に置いて設計されなければなりません。また、微分可能プログラミングは文化でもあり、確率的勾配降下法と上手く連携するためのヒントやコツの集合体です。総じて、微分可能プログラミングは機械学習の分野の中でも比較的取り組みやすい技術です。それでも、このパラダイムを習得し、実運用でスムーズに動かすには、ある程度の技量が必要です.
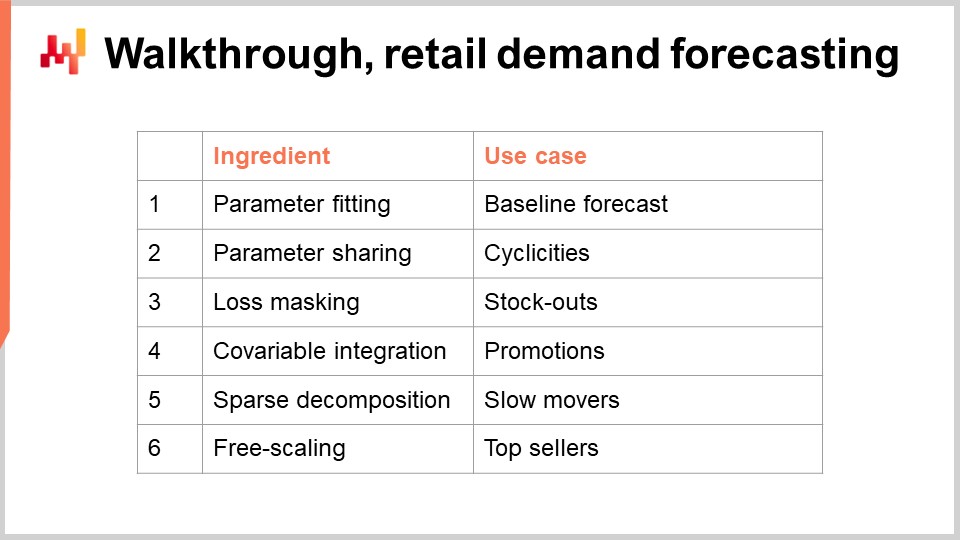
これで講義の第二部、ウォークスルーに着手する準備が整いました。ここでは、小売需要予測タスクのウォークスルーを行います。このモデリング演習は、前回の講義で提示した予測チャレンジと一致しています。簡単に言えば、小売ネットワークにおけるSKUレベルの日々の需要を予測したいのです。SKU、または在庫管理単位は、技術的には商品と店舗の直積であり、品揃えのエントリーに沿ってフィルタリングされたものです。たとえば、店舗が100軒、商品が10,000種類あり、全店舗にすべての商品が存在する場合、結果として100万のSKUが得られます.
決定論的な推定値を確率的なものに変換するツールが存在します。前回の講義では、ESSM手法を通じてそのうちの一つを見ました。次回の講義では、推定値を確率的推定値に変換するというこの具体的な問題について、さらに詳細に再検討します。しかし、今日のところは平均の推定にのみ注目し、その他の推定種類(分位点、確率的推定値など)は、本日提示する核となる例の自然な拡張として後で扱います。このウォークスルーでは、単純な需要予測モデルのパラメータを学習します。このモデルの単純さは一見すると誤解を招くかもしれませんが、実際にはこの種のモデルが2020年のM5予測コンペティションで示されたように、最先端の予測性能を実現しているのです.

パラメトリックな需要モデルでは、各SKUごとに1つのパラメータを導入します。これは極めて単純なモデルで、需要が各SKUに対して定数としてモデル化されます。しかし、この定数はすべてのSKUで同一というわけではありません。一度この一定の日次平均値が得られると、そのSKUのライフサイクル全体を通じて同じ値となります.
微分可能プログラミングを用いてこれがどのように実現されるか見てみましょう。1行目から4行目では、以前と同様にモックデータブロックを導入しています。実際には、このモデルおよびそのすべての変種は、ERP、WMS、TMSなど、ビジネスシステムから得られる入力に依存します。ERPから得られるデータの現実的な表現に数学モデルを組み込んで講義を行うと、今回の主題とは無関係な多数の偶発的な複雑さが生じるため、本講義では、実際の小売状況で観測されるようなデータを装うことなく、あえて現実味のないモックデータブロックを導入しています。このモックデータの唯一の目的は、テーブルとテーブル内の関係性を紹介し、提示されたコード例が完全でコンパイルおよび実行可能であることを保証することにあります。これまでに示したすべてのコード例は完全にスタンドアロンであり、前後に隠された部分は一切ありません。モックデータブロックの唯一の目的は、独立したコード片を確実に持つことです.
このウォークスルーのすべての例では、最初にこのモックデータブロックから始めます。1行目では “dates” を主キーとする日付テーブルを導入しています。ここでは、おおよそ2年と1か月の日付範囲を持っています。次に、2行目でSKUのリストであるSKUsテーブルを導入しています。このミニマルな例ではSKUは3つだけです。実際の大規模な小売ネットワークでは、SKUは数百万、いや数千万に及ぶでしょう。しかしここでは例のために非常に少ない数を採用しています。3行目では、SKUと日付の直積である “T” テーブルを用意しています。基本的に、この “T” テーブルから得られるのは、すべてのSKUとすべての日付が並んだ行列であり、2次元です.
6行目では、実際の自動微分ブロックを導入します。観測テーブルはSKUsテーブルであり、ここでの確率的勾配降下法は一度に1つのSKUを選択します。7行目では、唯一のパラメータとなる “level” を導入します。これはベクトルパラメータであり、これまでの自動微分ブロックではスカラーのパラメータしか導入していませんでした。以前のパラメータは単なる数値でしたが、ここでの “SKU.level” は実際には各SKUごとの1つの値をもつベクトルであり、これがSKUレベルでモデル化された定常的な需要を表しています。値の範囲も指定しており、その理由は後ほど明らかになります。このパラメータは最低0.01でなければならず、日次平均需要の上限として1,000を設定しています。このパラメータは自動的に1に近い値で初期化され、適切な出発点となります。このモデルでは、SKUごとにたった1つの自由度しかありません。最後に、8行目と9行目で実際にモデル自体を実装しています。8行目では “dot.delta” を計算しており、これはモデルで予測された需要から観測値 “T.sold” を引いたものです。モデルは単一の項、すなわち定数で、その後に観測値 “T.sold” が続きます.
ここで何が起こっているのか理解するために、いくつかのブロードキャスティングの挙動が見られます。“T” テーブルはSKUと日付のクロステーブルです。自動微分ブロックは観測テーブルの各行を反復処理しています。9行目では自動微分ブロック内にいるため、SKUテーブルから1行が選ばれています。このとき “SKUs.level” の値はベクトルではなく、観測テーブルの1行だけを選んだための単一のスカラー値となります。そして “T.sold” も、すでに1つのSKUが選ばれているため、行列ではなくなります。結果、“T.sold” は実際には日付に沿ったベクトルとなり、この差分 “SKUs.level - T.sold” を計算すると、日付テーブルに整合したベクトルが得られ、それを “D.delta” に代入します。これは、2年と1か月の日数ごとに1行あるベクトルです。そして最終的に、9行目で損失関数、つまり平均二乗誤差を計算しています。このモデルは非常にシンプルです。では、カレンダーパターンに関してはどうなるのでしょうか.

パラメータ共有は、おそらく最も単純で有用な微分可能プログラミング技法の一つです。パラメータが複数の観測行に貢献する場合、そのパラメータは共有されていると言います。観測間でパラメータを共有することで、勾配降下を安定させ、過学習の問題を軽減することができます。曜日パターンを例にとると、各SKUに対して様々な重みを表す7つのパラメータを導入することが考えられます。これまで、1つのSKUには定常需要のみの1つのパラメータしか持たせていませんでした。需要の認識をより豊かにするために、曜日ごとに固有の重みを持たせ、1週間7日分、7つの重みを乗算的に適用することが可能です.
しかし、すべてのSKUが固有の曜日パターンを持つとは限りません。実際には、プロダクトファミリー、プロダクトカテゴリー、サブカテゴリー、あるいは店舗内の部署など、曜日パターンを正確に捉えるカテゴリーや階層構造が存在すると仮定するのがはるかに合理的です。つまり、SKUごとに7つのパラメータを導入するのではなく、各カテゴリーごとに7つのパラメータを導入し、曜日パターンにおいて均質な挙動があると仮定するのです.
もしこれら7つのパラメータをレベルに対する乗算的効果として導入するなら、これは前回の講義でこのモデルに対して採用されたアプローチと全く同じで、M5コンペティションにおいてSKUレベルで第1位を獲得したものです。我々は定数のレベルと、曜日パターンに対する乗算的効果を持っています.
コードでは、1行目から5行目までで前述のモックデータブロックがあり、さらに “category” という追加テーブルを導入しています。このテーブルはSKUのグループ化テーブルであり、概念的にはSKUテーブルの各行に対して、カテゴリー・テーブル内にただ1つの対応行が存在します。Envision言語では、カテゴリーはSKUテーブルの上流にあると言います。7行目では曜日テーブルを導入しています。このテーブルは極めて重要で、捉えたい周期性パターンを反映する特定の形状で導入されています。7行目では、日付を7で割った余りに基づいて日付を集計することで、曜日テーブルを作成しています。これにより、正確に7行を持つテーブルが生成され、その7行は1週間の7曜日それぞれを表します。日付テーブルの各行に対して、データベース内の曜日テーブルの各行にはただ1つの対応行が存在することになります。したがって、Envision言語に従えば、曜日テーブルは “date” テーブルの上流に位置します.
次に “CD” テーブルがあります。これはカテゴリーと曜日の直積です。行数としては、曜日が7行あるため、カテゴリー数×7行となります。12行目では “CD.DOW” (DOWは曜日の略)という新たなパラメータを導入します。これはCDテーブルに属する別のベクトルパラメータです。自由度の観点では、ちょうどカテゴリー数に7を掛けた数のパラメータ値を持つことになり、これが求めるものであります。つまり、SKUごとではなく、各カテゴリーごとに1つのパターンでこの曜日パターンを捉えるモデルを目指しています.
このパラメータを宣言し、“in” キーワードを用いて “CD.DOW” の値が0.1から100の間にあることを指定します。13行目では、モデルで表現された需要を記述しています。需要は “SKUs.level * CD.DOW” として表され、これが需要そのものを示します。ここで、需要から観測値 “T.sold” を引いたものがデルタとなり、そこで平均二乗誤差を計算します.
13行目では、多くのブロードキャスティングの魔法が働いています。“CD.DOW” はカテゴリーと曜日のクロステーブルです。自動微分ブロック内にいるため、CDテーブルはカテゴリーと曜日のクロステーブルとなります。また、自動微分ブロックはSKUsテーブルを反復しているため、1つのSKUを選ぶと事実上1つのカテゴリーが選ばれたことになります(カテゴリー・テーブルは上流にあるため)。つまり、“CD.DOW” はもはや行列ではなく、7次元のベクトルとなります。しかし、“date” テーブルの上流にあるため、その7行が日付テーブルにブロードキャストされます。このブロードキャストは、曜日テーブルの各行が日付テーブルの特定の行と結びついているため、一通りの方法しかありません。結果として、二重のブロードキャストが行われ、最終的にSKUに対して曜日単位の周期性を持つ一連の需要値が得られます。これが現時点での我々のモデルであり、損失関数の他の部分に変更はありません.
Envisionのリレーショナルな特性から得られるブロードキャスティングの挙動と微分可能プログラミングの機能を組み合わせることで、周期性に非常にエレガントに取り組む方法が見出せます。カレンダーの周期性は、わずか3行のコードで表現可能です。この手法は、非常にスパースなデータを扱う場合でも優れた性能を発揮します。たとえ月平均1単位しか売れない製品であっても問題なく動作するでしょう。そのような場合、数十もしくは数百の製品を含むカテゴリーを設けるのが賢明なアプローチです。この技法は、年間の月や月内の日といった他の周期パターンを反映するためにも利用可能です.
前回の講義で紹介されたモデルは、M5コンペティションで最先端の成果を達成したもので、曜日、年間の月、月内の日という3つの周期性を乗算的に組み合わせたものです。これらのパターンはすべて、乗算として連鎖されています。他の2つのバリエーションの実装は、注意深い皆さんに委ねられていますが、各周期パターンごとに数行のコードで済むため、非常に簡潔です.

前回の講義では、販売予測モデルを紹介しました。しかし、私たちが関心を持つのは売上ではなく、需要です。売上がゼロであることと需要がゼロであることを混同すべきではありません。ある日に店舗で顧客が購入できる在庫がなかった場合、ロカドでは欠品に対処するためにロスマスキング手法が用いられます。これは欠品に対処する最も単純な手法ですが、唯一のものではありません。私の知る限り、生産現場では少なくとも他に2つの手法が使われており、それぞれに利点と欠点があります。これらの手法は本日は扱いませんが、後の講義で取り上げる予定です。
コード例に戻ると、1行目から3行目はそのままです。続く部分を見ていきましょう。6行目では、在庫状況を示すブール値フラグでモックデータを充実させています。各SKUおよび各日に対して、その日の終わりに店舗で欠品が発生したかどうかを示すブール値が存在します。15行目では、終日の欠品が観測された日をゼロにして除外するようにロス関数を修正しています。これにより、欠品の発生によるバイアスがある状況下で勾配が逆伝播されないことを保証しています。
ロスマスキング手法の最も不可解な点は、モデル自体を変更しないことにあります。実際、14行目で表現されるモデルは全く同じで、一切の変更が加えられていません。変更されるのはロス関数そのものだけです。この手法は単純ですが、モデル中心の視点からは大きく逸脱しています。根本的には、モデリング中心の技法です。欠品によるバイアスを認識し、それをモデリングに反映させることで状況を改善しようとしています。しかし、実際に変更しているのはモデル自体ではなく、最適化するロスです。つまり、このモデルは純粋な数値誤差の観点からは他のモデルと比較できなくなってしまいます。
前回の講義で説明したようなウォルマートのような状況では、ロスマスキング手法はほとんどの製品にとって十分です。経験則として、需要が常に1単位しか在庫されていないほどまばらでなければ、この手法はうまく機能します。さらに、欠品が非常に頻繁な製品は避けるべきです。というのも、それらは小売業者が日末に欠品状態になることを明示的に狙った戦略であるからです。これは、特に極めて鮮度の高い製品で、日末に在庫切れ状態を狙う場合によく見られます。これらの制限を補う代替手法もありますが、今日は取り上げる時間がありません。

プロモーションは小売において重要な要素です。より一般的には、小売業者が需要に影響を与え、形成する方法は、価格設定や商品のゴンドラへの移動など数多く存在します。予測のための追加情報を提供する変数は、サプライチェーン分野では通常、共変量(covariates)と呼ばれます。天気データやソーシャルメディアデータのような複雑な共変量に対しては楽観的な考えが多く見られます。しかし、より高度なトピックに入る前に、明らかに需要に大きな影響を与える価格情報といった、部屋の中の象に対処する必要があります。したがって、このコード例の7行目および14行目で、「category.ed」を導入しています。ここで「ed」は需要の弾力性(elasticity of demand)を意味します。これは各カテゴリーごとに1つの自由度を持つ共有ベクトルパラメータであり、需要の弾力性を表現するためのものです。16行目では、価格弾力性の指数関数形式、すなわち(-category.ed * t.price)の指数として導入しています。直感的には、この形式では価格が上昇すると指数関数の効果により需要が急速にゼロに収束し、逆に価格がゼロに近づくと需要は爆発的に増加します。
この指数関数形式の価格反応は単純ですが、パラメータを共有することで、モデル内でこのような指数関数を使用しても高い数値安定性が保たれます。実際、特にウォルマートのような状況下では、割引や通常価格との差分、供給者によるマーケティング施策を表す共変量、またはゴンドラなどを取り入れるカテゴリ変数など、複数の価格情報が存在します。微分可能プログラミングを使えば、状況に応じた任意に複雑な価格反応を構築することは非常に容易です。ほぼあらゆる種類の共変量を統合することが簡単にできます。

動きの遅い商品は、小売やその他多くの業界において避けられない現実です。これまでに紹介したモデルは、SKUごとに1つのパラメータ、すなわち1つの自由度を持っており、共有パラメータを含めればさらに多くなります。しかし、年に1回または数回しか回転しないSKUの場合、SKUごとに1つの自由度さえも確保できないため、解決策は共有パラメータのみに依存し、SKUレベルの自由度を持つすべてのパラメータを排除することにあります。
2行目と4行目では、「products」と「stores」という2つのテーブルを導入し、テーブル「SKUs」は、productsとstoresの直積をフィルタリングしたサブテーブルとして構築されます。これは品揃えの定義そのものです。15行目と16行目では、製品テーブルに親和性を持つレベルと、店舗テーブルに親和性を持つレベルという、2つの共有ベクトルパラメータを導入しました。これらのパラメータは、最大値である0.01から100という特定の範囲内で定義されています。
さて、18行目では、SKUごとのレベルは製品レベルと店舗レベルの掛け算によって構成されています。残りのスクリプトは変更されていません。では、どのように機能するのでしょうか?19行目では、SKU.levelはスカラー値です。観測テーブルであるSKUsテーブルを反復するautodeskブロックが存在します。したがって、18行目のSKUs.levelは単なるスカラー値です。次にproducts.levelがあります。productsテーブルはSKUsテーブルの上流に位置するため、各SKUに対して該当する製品は一つだけです。よって、products.levelは単なるスカラー数値です。同様に、SKUsテーブルの上流にあるstoresテーブルにも同じことが言えます。18行目では、この特定のSKUに紐づく店舗は1つだけです。したがって、私たちが得るのは2つのスカラー値の掛け算であり、それがSKU.levelとなります。残りのモデルは修正されていません。
これらの手法は、時に「データが足りない」または「データがまばらすぎる」という主張に全く新しい視点を提供します。実際、微分可能な観点からは、そのような主張はあまり意味を持ちません。絶対的な意味でデータが少なすぎるとかまばらすぎるということはなく、単にまばら性、あるいは極端なまばら性に向けて調整可能なモデルが存在するだけです。課せられた構造は、学習プロセスを可能にするだけでなく、数値的に安定させるためのガイドレールのような役割を果たします。
ゼロから機械学習モデルがすべてのパターンを発見しようとする他の手法と比べ、この構造化アプローチは学習すべき構造そのものを確立します。したがって、ここで作用している統計的メカニズムは、学習すべき内容に対する自由度が制限されます。その結果、データ効率の面では非常に効率的になり得ます。もちろん、これらすべては適切な構造を選択していることに依存しています。
ご覧のように、実験を行うことは非常に簡単です。すでに非常に複雑なことに取り組んでおり、50行未満で、かなり複雑なウォルマートのような状況に対応できるのです。これは大きな成果です。多少の経験的プロセスはありますが、実際のところその規模はほんの数十行です。企業の運営に関わるERP、すなわち大規模な小売ネットワークでは、通常、1000のテーブルとテーブルごとに100のフィールドが存在することを念頭に置いてください。したがって、この構造化予測モデルの複雑さに比べ、業務システムの複雑さは途方もなく大きいのです。もし反復に少々時間を要しても、それはほとんど問題になりません。
さらに、M5予測コンペティションで実証されたように、サプライチェーンの実務者はすでにパターンを把握しています。M5チームが曜日、月、日の3つのカレンダーパターンを使用したとき、これらのパターンはどの経験豊富なサプライチェーン実務者にとっても自明のものでした。サプライチェーンの現実は、隠れたパターンを発見しようとしているわけではなく、例えば価格を大幅に下げれば需要が大幅に増加するという事実は誰も驚かせません。残る疑問は、効果の大きさと反応の正確な形状がどうなっているかだけです。これらは比較的技術的な詳細ですが、少し実験を行う余裕があれば、これらの問題は比較的容易に解決できます。
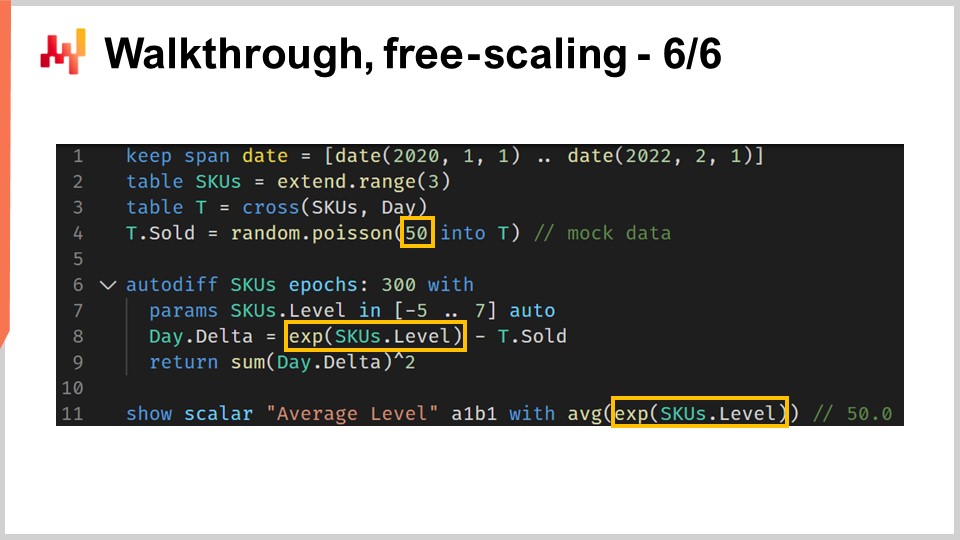
このウォークスルーの最後のステップとして、微分可能プログラミングの小さな癖について指摘しておきます。微分可能プログラミングは、一般的な数学的最適化ソルバーと混同してはなりません。勾配降下法が進行していることを念頭に置く必要があります。より具体的には、パラメータを最適化および更新するために用いられるアルゴリズムは、ADAMアルゴリズムに付随する学習率と同じ最大降下速度を持っています。Envisionでは、デフォルトの学習率は0.01です。
コードを見ると、4行目で販売数量が平均50のポアソン分布からサンプリングされる初期化を導入しています。もしレベルを学習したい場合、技術的には50程度の値を持つレベルが必要です。しかし、パラメータを自動初期化すると、値は約1から始まり、0.01刻みでしか増加できません。そのため、実際に50に到達するには約5,000エポック必要となります。共有されないパラメータであるSKU.levelの場合、このパラメータは各エポックで1度しか触れられないため、5,000エポックが必要となり、計算速度が不必要に遅くなります。
降下を速めるために学習率を上げるという解決策も考えられます。しかし、学習率を膨張させることは通常、適切なアプローチではないため推奨しません。実際の状況では、この共有されないパラメータに加え、共有パラメータも存在します。これらの共有パラメータは、各エポック中に確率的勾配降下法によって何度も更新されます。もし学習率を大幅に上げると、共有パラメータに対して数値的不安定性が生じるリスクがあります。SKUレベルの更新速度を上げたとしても、他のパラメータの数値安定性に問題が発生する可能性があります。
より良い手法としては、リスケーリングのトリックを用い、パラメータを指数関数で包む方法があります。これがまさに8行目で実施されていることです。このラッパーを用いることで、レベルのパラメータ値を非常に低い値または非常に高い値に、より少ないエポック数で到達できるようになります。この癖(クワーク)は、本ウォークスルーで現実的な小売需要予測の例を示すために導入する必要がある、ほぼ唯一の癖です。結局のところ、これは些細な癖に過ぎません。それにもかかわらず、微分可能プログラミングでは勾配の流れに注意を払う必要があるということを改めて思い出させてくれます。微分可能プログラミングは全体として流動的な設計体験を提供しますが、魔法ではありません。
締めくくりとして、構造化モデルは最先端の予測精度を実現しているという点を挙げておきます。この点は前回の講義で広く論じられました。しかし、今日提示された要素に基づくと、構造化パラメトリックモデルを用いた微分可能プログラミングにおいて、精度自体が決定的な要因ではないと主張できます。私たちが得るのは「理解」であり、単に予測を行うソフトウェアを得るのではなく、捉えようとしているパターンそのものに対する直接的な洞察を得るのです。例えば、今日紹介したモデルは、曜日ごとの明示的な重み付けと需要の弾力性を伴った需要予測を直接提供します。もしこの需要に、たとえばブラックフライデーに関連する上昇分、すなわち毎年同じ時期に起こるわけではない準季節性のイベントを導入する場合、それも可能です。単に因子を追加すれば、曜日パターンなど他のパターンから独立したブラックフライデーの上昇分の推定が得られます。これは非常に重要な点です。
構造化アプローチによって得られるのは、生のモデルそのもの以上の「理解」です。例えば、負の弾力性、すなわち価格を上げると需要が増えるという結果になった場合、ウォルマートのような状況ではこれは非常に疑わしい結果です。おそらく、これはモデルの実装に欠陥があるか、根本的な問題があることを示しているでしょう。精度指標が何を示そうとも、もし製品の値段を上げることで購入数が増えるという結果が出た場合は、データパイプライン全体に疑問を持つべきです。これこそが「理解」ということです。
また、モデルは変化に対応可能です。微分可能プログラミングは非常に表現力豊かです。現在のモデルは、ひとつの過程の一回の反復に過ぎません。市場が変革する場合や企業自体が変わる場合でも、現行のモデルが自然にその進化を捉えることができると信頼できます。自動進化なんてものは存在せず、この進化を捉えるにはサプライチェーン-サイエンティストの努力が必要です。しかし、その努力は比較的最小限に抑えられると期待できます。つまり、非常に小さく整然としたモデルであれば、後でその構造を再調整する際の作業は、巨大なエンジニアリングの塊であるモデルと比べて、はるかに小さいものになるということです.
慎重に設計された場合、微分可能プログラミングによって生成されたモデルは非常に安定しています。この安定性は、構造の選択に帰着します。微分可能プログラミングによって最適化されるプログラムでは、安定性は自動的に得られるものではなく、パラメータに特定の意味論がある非常に明快な構造が存在する場合にのみ得られるものです。例えば、モデルを再学習するたびに曜日ごとの重みが全く異なる値になるようなモデルがあるとすると、実際のビジネス環境はそこまで急激に変化していないはずです。モデルを2回実行すれば、曜日ごとの値はかなり安定しているはずです。もしそうでなければ、需要のモデリング方法に何か大きな問題があるということになります。したがって、モデルの構造を賢明に選択すれば、非常に安定した数値結果を得ることができます。これにより、サプライチェーンの文脈で複雑な機械学習モデルを使用する際に陥りがちな落とし穴を回避することができます。実際、サプライチェーンの観点からすれば、数値的不安定性は至って致命的で、各所でラチェット効果が発生します。需要の推定値が変動すれば、根拠のない購買注文や生産注文がランダムに発生してしまうことを意味します。一度生産注文が出されると、翌週になって「それは間違いだった」と取り消すことはできません。あなたはその決定に縛られてしまうのです。未来の需要を推定する指標が不安定であれば、在庫補充(replenishment)や生産注文が膨張してしまうでしょう。この問題は、設計段階で安定性を確保することで解決可能です。
機械学習を実際の運用に導入する上で最大の障壁のひとつは信頼です。数百万ユーロやドルを運用する際、数値レシピで何が起こっているのかを理解することは極めて重要です。サプライチェーンでのミスは非常に高額な損失を招く可能性があり、理解不足なアルゴリズムの誤用によって引き起こされたサプライチェーンの災害の例も多く存在します。微分可能プログラミングは非常に強力ですが、それによって構築されるモデルは信じられないほどシンプルです。これらのモデルは、通常、分岐や関数を含む単純な乗算モデルであり、実際にはExcelのスプレッドシート上で実行することも可能です。Excelスプレッドシートに搭載できない唯一の要素は自動微分ですが、もちろん、数百万のSKUがある場合にはスプレッドシートでこれを試みるべきではありません。しかしそのシンプルさは、スプレッドシートに記入する内容と非常に相性が良いのです。このシンプルさこそが信頼の確立を促し、機械学習を単なる派手なプロトタイプではなく実際の運用に持ち込む大きな要因となります。
最後に、これらの全ての特性を組み合わせることで、非常に高精度な技術が得られます。この視点は、本講義シリーズの最初の章で議論されました。我々はサプライチェーンに投入されるすべての努力を、使い捨ての資源として扱うのではなく、資本主義的な投資として位置付けたいと考えています。このアプローチにより、これらの取り組みを投資とみなし、時間の経過とともに投資収益を生み出し続けることができます。微分可能プログラミングは、サプライチェーンにおける資本主義的視点と非常に相性が良いのです。

第2章では、「実験的最適化」と題された重要な講義を紹介しました。この講義は、サプライチェーンにおいて実際に改善し、より良い成果を出すとはどういうことかという、シンプルでありながら根本的な疑問に対するひとつの可能な回答を示しています。微分可能プログラミングの視点は、サプライチェーンの実務者が直面する多くの課題に対して非常に具体的な洞察を提供します。企業のソフトウェアベンダーは、サプライチェーンの失敗の原因をしばしば悪いデータに求めます。しかし、私はこれは問題の見方を誤っているに過ぎないと考えています。データはそれ自体であり、あなたのERPシステムはデータサイエンス向けに設計されてはいないものの、何年も、場合によっては何十年もスムーズに運用され、社内の人々はそれを使ってサプライチェーンを管理しています。たとえ、サプライチェーンに関するデータを収集するあなたのERPシステムが完璧でなくとも問題ありません。完璧なデータが得られると期待するのは、ただの空想に過ぎないのです。サプライチェーンは非常に複雑な世界であり、そのためシステムも完璧ではないのです。現実的には、ひとつの業務システムだけでなく、せいぜい六つ程度が存在し、これらは完全に一致しているわけではありません。これは単なる現実です。しかし、企業ベンダーが悪いデータを非難するとき、その背後には企業に関する特定の前提のもとで設計された予測モデルが存在しているのが実情です。もしあなたの企業がその前提のいずれかに反する場合、その技術は完全に崩壊してしまいます。この状況では、非合理的な前提条件を持った予測モデルにデータを投入しても、完璧ではないために技術が崩壊するのです。企業側に問題があるとするのは全く合理的ではありません。問題なのは、サプライチェーンの文脈においてありえないデータを前提とする、ベンダーが推し進める技術そのものなのです。
本日は精度指標に関するベンチマークを一切提示しませんでした。しかし、私の主張は、これらの精度指標はほとんど重要ではないということです。予測モデルは意思決定を推進するためのツールに過ぎません。重要なのは、何を購入し、何を生産し、価格を上げるか下げるかといった、意思決定が良いか悪いかという点です。確かに、悪い意思決定は予測モデルに起因することもあります。しかし、ほとんどの場合、それは精度の問題ではありません。例えば、ある売上予測モデルがあり、適切に管理されていなかった在庫切れの視点を修正しました。しかし、在庫切れの視点を修正したときに、実際には精度指標自体を修正したのです。すなわち、予測モデルを修正することは必ずしも精度の向上を意味するのではなく、多くの場合、実際に直面している問題や視点を根本から見直し、精度指標やそれ以上の部分を変更することになるのです。従来の視点の問題は、精度指標が立派な目標であると仮定している点にあります。それは必ずしも正しいとは言えません。
サプライチェーンは現実の世界で機能しており、予期せぬ出来事や奇想天外な事態が数多く発生します。例えば、船によるスエズ運河の閉塞のような事態は全く予想外の出来事です。そのような状況では、この地域に関連する全てのリードタイム予測モデルが即座に無効化されてしまいます。もちろん、これはこれまで実際に起こったことがなかったため、そのような状況下ではバックテストを行うことはできません。しかし、たとえ船がスエズ運河を塞ぐという極端な状況であっても、本日提案しているようなホワイトボックスアプローチを採用していれば、モデルを修正することは可能です。この修正にはある程度の推測が伴いますが、それで問題はありません。全く間違っているよりは、おおよそ正しい方が良いのです。例えば、スエズ運河が閉塞している場合、「このルートを通る全ての供給品についてリードタイムを1か月延長しよう」と単純に決定することができます。これは非常に大雑把な対応ですが、すでに情報がある状態で全く遅延がないと仮定するよりは良いのです。さらに、変化は内部から頻繁に生じます。例として、1つの古い流通センターと、数十の店舗に供給する新しい流通センターを持つ小売ネットワークを考えてみましょう。店舗への供給品が基本的に古い流通センターから新しい流通センターへ移行している状況が進行しているとします。このような状況は、特定の小売業者の歴史上ほとんど一度しか起こらず、バックテストは現実的に不可能です。しかし、微分可能プログラミングのようなアプローチを採用すれば、このような段階的な移行に合致するモデルを実装することは全く容易です。

結論として、微分可能プログラミングは未来に対する洞察を体系化するためのアプローチを提供する技術です。微分可能プログラミングは、文字通り未来の見方自体を形作ることを可能にします。これは認識(perception)の側面に位置しており、この認識に基づいてより良いサプライチェーンの意思決定を下すことができ、その意思決定が行動(action)を駆動するのです。主流のサプライチェーン理論における最大の誤解のひとつは、認識と行動を完全に独立した要素として扱えるという考え方です。例えば、計画(認識)を担当するチームと、在庫補充(行動)を担当する独立したチームを設ける形がそれにあたります。
しかし、認識と行動のフィードバックループは非常に重要であり、最も大切な要素です。これは、正しい認識へと導く仕組みそのものなのです。このフィードバックループがなければ、あなたが見ているものが本当に正しいのか、あるいはあなたが思っているものなのかすら判断できません。このフィードバック機構は不可欠であり、これを通してサプライチェーンの行動に即した正確な未来の定量的評価へとモデルを導くことができるのです。主流のサプライチェーンアプローチは、基本的に非常に硬直した予測手法に固執しているため、この点をほぼ完全に見落としています。一つの予測モデルに固執すれば、行動側から得られる全てのフィードバックは無意味となり、それを無視する以外に手立てがなくなってしまうのです。
もし特定の予測モデルに固執しているなら、行動から得られる情報を受けてモデルを再構成することはできません。一方で、微分可能プログラミングは、その構造化モデリングアプローチにより、全く異なるパラダイムを提供します。予測モデルは完全に使い捨て可能なものであり、そのすべてを自由に変更することができます。もし行動からのフィードバックが、予測の視点に根本的な変更を要求するのであれば、単にその根本的な変更を実装すれば良いのです。特定のモデルのバージョンに固執する必要はありません。モデルを非常にシンプルに保つことは、運用段階において継続的に変更可能なオプションを保持するために大いに役立ちます。というのも、構築したモデルが巨大で工学的な怪物のようなものであれば、運用後に変更するのは非常に困難になるからです。継続的な変更を可能にするための重要な要素は、コード行数や内部の複雑さにおいて非常に節約されたモデルである必要がある点にあります。これが微分可能プログラミングの真価を発揮するところです。高い精度を追求するのではなく、高い関連性を達成することが重要なのです。関連性がなければ、どんな精度指標も全く意味をなさなくなります。微分可能プログラミングと構造化モデリングは、関連性を達成し、その関連性を時間の経過とともに維持するための道筋を提供してくれます。

本日の講義はこれで終了します。次回は3月2日、同じ時間、パリ時間午後3時に、サプライチェーンのための確率的モデリングについて発表します。単に一つの未来を選定してそれを正しいと宣言するのではなく、あり得るすべての未来を検討することの技術的な意味合いにより近づきます。実際、サプライチェーンをリスクに対して効果的に強靭なものにするためには、あり得るすべての未来を考慮することが非常に重要です。もし一つの未来だけを選べば、予測が完璧でない限り、非常に脆弱なシステムになってしまいます。ご存知の通り、予測が完全に正しいことは決してありません。だからこそ、あらゆる可能性のある未来を検討するという考えを取り入れることが非常に重要であり、現代の数値レシピを用いてその方法を考察していきます。
質問: 局所的な極小値を避けるために確率的ノイズが加えられますが、どのように活用またはスケールして、大きな逸脱を防ぎ、勾配降下法が目標から大きく逸脱しないようにしているのでしょうか?
非常に興味深い質問です。この回答には2つの側面があります。
まず第一に、これがAdamアルゴリズムが勾配ステップの大きさにおいて非常に保守的である理由です。勾配は本質的に無限であり、数千、あるいは数百万といった値になる可能性があります。しかし、Adamでは最大ステップが学習率によって上限が定められているため、実質的にAdamは文字通り最大ステップを強制する数値レシピを提供し、それによって大規模な数値的不安定性を回避できるのです。
さて、学習率が設定されているにもかかわらず、単なる変動によって一度に一ステップずつ反復的に動くものの、その多くが誤った方向に進む可能性も否定できません。だからこそ、確率的勾配降下法はまだ完全には理解されていないと言えるのです。実際の運用では非常にうまく機能していますが、なぜそれほど効果的に働くのか、なぜ極めて速く収束するのか、またどうしてもっと多くの問題が発生しないのかは、特に高次元空間で動作することを考えると、完全には解明されていません。通常、実際には何十、場合によっては何百ものパラメータが各ステップで調整されるのです。2次元や3次元で直感的に考えると非常に誤解を招きやすく、高次元では物事の挙動が全く異なるのです。
つまり、この質問の本質は非常に重要です。一方では、Adamの勾配ステップの大きさに対する極めて保守的な性質があり、もう一方ではその仕組みは十分に理解されていないものの、実際には非常にうまく機能しているという側面があります。ちなみに、確率的勾配降下法が完全には直感的でないという事実こそが、この手法が約70年間知られていたにもかかわらず効果的だと認識されなかった理由でもあると考えています。約70年間、人々はこの手法の存在を知っていたものの非常に懐疑的であり、深層学習の大成功がコミュニティに対して「実際に非常に効果的に機能している」と認識させたのです。
Question: あるパターンが弱く、したがってモデルから削除すべきであると判断するにはどうすればよいでしょうか?
再び、非常に良い質問です。厳密な基準は存在せず、実際にはサプライチェーン・サイエンティストの判断に委ねられるものです。もし導入したパターンがごくわずかな利益しかもたらさず、コード上はたった2行で計算時間に関しても無視できる影響しかない場合、また将来的にそのパターンを除去するのが半ば容易であれば、「まぁ、残しておいても問題はなさそうだ。大きな害はなく、悪くもない。今は弱いかもしれないが、状況によってはこのパターンが強く転じる可能性もある」と考えるでしょう。保守性の観点からはそれで問題ありません。
しかしながら、捉える要素が少なく、モデルに多大な計算負荷を加えるパターンも存在します。一度にパラメータやロジックを追加するたびに、必要な計算リソースが膨張し、モデルはより遅く、扱いづらくなります。もしこの弱いパターンが悪い方向に強化され、予測モデリングにおいて不安定性を引き起こし、混乱を招くと考えるなら、通常は「いや、削除すべきだ」と判断する状況です。
ご覧の通り、本当に判断の問題なのです。差分可能プログラミングは一種の文化であり、あなたは一人ではありません。Lokadでは、同僚や仲間たちが様々なアプローチを試みており、これこそが私たちが育成しようとしている文化です。全能のAIという、全ての問題を解決する人工知能の視点と比べると、少し期待外れに感じるかもしれませんが、実際のところサプライチェーンは非常に複雑で、私たちの人工知能手法はまだ粗削りであるため、人間の知性に代わる現実的な代替手段は存在しないのです。ここでいう判断とは、あらゆるアルゴリズムのトリックでは全く満足のいく答えにたどり着けないため、適用可能な非常に人間的な知性が必要である、という意味です。
とはいえ、何らかのツールを設計できないというわけではありません。それはまた別の話題になりますが、Lokadで提供している設計支援ツールについて実際に取り上げるかどうかは今後の検討次第です。判断を下す必要がある場合に備え、必要な計測機能をすべて提供し、サプライチェーン・サイエンティストが現状のモデルの運命について決断を下す際の苦労を最小限に抑えようという考え方です。
Question: 機械学習や差分可能プログラミングが大幅に良い結果をもたらすための、サプライチェーンの複雑性の閾値は何でしょうか?
Lokadでは、年間売上高が1000万ドル以上の企業に対して、実質的な成果をもたらすことが多いです。私の考えでは、年間売上高が5000万ドル以上の企業になると、本当の意味でその効果が発揮され始めます。
その理由は、根本的に非常に信頼性の高いデータパイプラインを構築する必要があるからです。ERPシステムから毎日すべての関連データを抽出できなければなりません。データが良いか悪いかはさておき、保持しているデータには多くの欠陥があるかもしれません。それでも、毎日基本的な取引データを抽出するための配管作業は膨大です。もし企業があまりにも小規模であれば、多くの場合専任のIT部門すら存在せず、信頼性の高い日次抽出が行えず、その結果、成果に大きな影響を及ぼします。
さらに、業種や複雑性の観点から言えば、私の意見では、多くの企業やサプライチェーンは最適化にすら着手していません。先に述べた通り、主流のサプライチェーン理論は、より正確な予測を追求すべきだと強調しています。予測誤差を低減することが目標であり、例えば多くの企業は計画チームや予測チームを編成して取り組んでいます。しかし、私の見解では、これらは本質的にビジネスに付加価値を生むものではなく、誤った問題設定に対する非常に洗練された回答を提供しているに過ぎません。
驚くかもしれませんが、差分可能プログラミングが際立つのは、それが根本的に非常に強力だからではなく、通常、企業にとって真に関連性のある仕組みが初めて導入されるからです。例えば、サプライチェーンで実装されるほとんどのモデルは、安全在庫モデルのように、実際のサプライチェーンとは全く無関係なものです。安全在庫モデルでは、リードタイムがマイナスになる、つまり「今注文しても昨日に届く」という前提に立っています。これは全く意味を成さず、その結果、安全在庫運用の成果は通常、満足のいくものにはなりません。
差分可能プログラミングが輝くのは、壮大な数値的優位性を達成したり、他の機械学習手法よりも優れているからではなく、複雑でカオスな、常に変化する半ば悪夢のような適用環境において、処理するデータに対して真に関連性のある解を提供できるからです。
これ以上質問はなさそうです。では、来月のサプライチェーンにおける確率的モデリング講義でお会いしましょう。


