Kontinuierlicher Rang-Wahrscheinlichkeits-Score (CRPS)

learn menu
Originally written by Joannes Vermorel, June 2016. -> Ursprünglich verfasst von Joannes Vermorel, Juni 2016. Updated by Alexey Tikhonov, May 2024. -> Aktualisiert von Alexey Tikhonov, Mai 2024.

Probabilistische Prognosen weisen jeder möglichen Zukunft eine Wahrscheinlichkeit zu. Dennoch sind nicht alle probabilistischen Prognosen gleich genau, und es werden Metriken benötigt, um die jeweilige Genauigkeit verschiedener probabilistischer Prognosen zu bewerten. Einfache Genauigkeitsmetriken wie MAE (Mean Absolute Error) oder MAPE (Mean Absolute Percentage Error) sind nicht direkt auf probabilistische Prognosen anwendbar. Der Continuous Ranked Probability Score (CRPS) verallgemeinert den MAE für den Fall probabilistischer Prognosen. Zusammen mit der Kreuzentropie ist der CRPS eine der am häufigsten verwendeten Genauigkeitsmetriken, wenn probabilistische Prognosen eine Rolle spielen.

Überblick

Der CRPS wird häufig verwendet, um die jeweilige Genauigkeit zweier probabilistischer Vorhersagemodelle zu bewerten. Insbesondere kann diese Metrik mit einem Backtesting Prozess kombiniert werden, um die Genauigkeitsbewertung durch die Nutzung mehrerer Messungen desselben Datensatzes zu stabilisieren.

Diese Metrik unterscheidet sich insbesondere von einfacheren Metriken wie dem MAE durch ihren asymmetrischen Ausdruck: Während die Prognosen probabilistisch sind, sind die Beobachtungen deterministisch. Im Gegensatz zur Pinball-Verlustfunktion konzentriert sich der CRPS nicht auf einen spezifischen Punkt der Wahrscheinlichkeitsverteilung, sondern betrachtet die Verteilung der Prognosen als Ganzes.

Formale Definition

Sei $${X}$$ eine Zufallsvariable.

Sei $${F}$$ die kumulative Verteilungsfunktion (CDF) von $${X}$$, sodass $${F(y)=\mathbf{P}\left[X \leq y\right]}$$.

Sei $${x}$$ die Beobachtung und $${F}$$ die der empirischen probabilistischen Prognose zugeordnete CDF.

Der CRPS zwischen $${x}$$ und $${F}$$ wird definiert als:

$$\qquad \qquad \qquad \qquad{CRPS(F, x) = \int_{-\infty}^{\infty}\Big(F(y)- 𝟙(y - x)\Big)^2dy} \qquad \qquad \qquad \qquad \qquad \qquad \tag{1}$$

wobei $${𝟙}$$ die Heaviside-Stufenfunktion ist und eine Stufenfunktion entlang der reellen Linie bezeichnet, die annimmt:

  • den Wert 1, wenn das reelle Argument positiv oder null ist,
  • den Wert 0 andernfalls.

Der CRPS wird in derselben Einheit wie die beobachtete Variable ausgedrückt (z.B., wenn die Nachfrage eines Produkts in Einheiten prognostiziert wurde, wird der CRPS ebenfalls in Einheiten angegeben).

Der CRPS verallgemeinert den mean absolute error (MAE). Tatsächlich reduziert er sich auf den MAE, wenn die Prognose deterministisch ist. Dieser Punkt wird in Diagramm D unten veranschaulicht.

Bekannte Eigenschaften

Gneiting und Raftery (2004) zeigen, dass der Continuous Ranked Probability Score äquivalent formuliert werden kann als:

$$\qquad \qquad \qquad \qquad {CRPS(F,x) = \mathbf{E}\Big[|X-x|\Big]-\frac{1}{2}\mathbf{E}\Big[|X-X^*|\Big]} \qquad \qquad \qquad \qquad \qquad \qquad \tag{2}$$

wobei

  • $${X}$$ und $${X^*}$$ unabhängige Kopien einer linearen Zufallsvariable sind,
  • $${X}$$ die mit der kumulativen Verteilungsfunktion $${F}$$ assoziierte Zufallsvariable ist,
  • $${\mathbf{E}[X]}$$ der Erwartungswert von $${X}$$ ist.

Numerische Auswertung

Aus numerischer Sicht besteht eine einfache Methode zur Berechnung des CRPS darin, das ursprüngliche Integral in zwei Integrale mit gut gewählten Grenzen aufzubrechen, um die Heaviside-Stufenfunktion zu vereinfachen, was ergibt:

$$\qquad \qquad \qquad \qquad{CRPS(F, x) = \int_{-\infty}^x F(y)^2dy + \int_x^{\infty}\Big(F(y)- 1\Big)^2dy} \qquad \qquad \qquad \qquad \qquad \tag{3}$$

In der Praxis, da $$F$$ eine durch ein Prognosemodell gewonnene empirische Verteilung ist, besitzt die entsprechende Zufallsvariable $${X}$$ eine kompakte Unterstützung, was bedeutet, dass es nur eine endliche Anzahl von Punkten gibt, bei denen $${\mathbf{P}[X = x] \gt 0}$$ gilt. Außerdem sind alle Werte von $$x$$ diskrete Zahlen. Somit können die Integrale in diskrete endliche Summen umgewandelt werden, wie in der unten stehenden Formel und in Diagramm B im nächsten Abschnitt dargestellt.

$$\qquad \qquad \qquad \qquad{CRPS(F, x) = \sum_{k=0}^x F(y_k)^2 + \sum_{x+1}^{n} (F(y_k) - 1)^2} \qquad \qquad \qquad \qquad \qquad \qquad \tag{4}$$

In der Formel (4) steht der Index $$n$$ für das letzte Element des rechten Endes einer Wahrscheinlichkeitsverteilung (z.B., der höchste Nachfragewert mit nicht-null Wahrscheinlichkeit).

Schließlich, da die CRPS-Berechnung für einen einzelnen Zeitpunkt durchgeführt wird, muss zur Berechnung des CRPS über einen bestimmten interessierenden Bewertungszeitraum (z.B., für das Verantwortlichkeitsfenster, welches sich aus der supplier Lieferzeit und der reorder Periode zusammensetzt) der Durchschnitt der für diesen Zeitraum berechneten CRPS-Werte herangezogen werden.

$$\qquad \qquad \qquad \qquad \qquad \qquad {CRPS = \frac{1}{T} \sum_{t=1}^{T} CRPS_t} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \tag{5}$$

Visuelle Intuition

Um die CRPS-Berechnung zu veranschaulichen, betrachten Sie das folgende Beispiel (siehe die unten stehenden Diagramme):

A: Zunächst haben wir eine probabilistische Nachfrageprognose unter Verwendung einer negativen Binomialverteilung erstellt und deren Ausläufer abgeschnitten, wenn die Wahrscheinlichkeiten unter 0,1% lagen (was extrem unwahrscheinliche Ereignisse darstellt, wie sie etwa einmal alle drei Jahre auftreten). Prognostizierte Nachfragewerte mit nicht-null Wahrscheinlichkeiten erstreckten sich über den Bereich von 1 bis 26 Einheiten. Später stellte sich heraus, dass die tatsächliche Nachfrage 15 Einheiten betrug (wie durch die vertikale rote gestrichelte Linie dargestellt).

B: Wir haben den CRPS gemäß der oben genannten vierten Formel berechnet (siehe “Numerische Auswertung”). Der resultierende CRPS-Wert stellt die Summe zweier Bereiche dar, die in hellrot gefüllt sind.

C: Wie in Diagramm A, jedoch mit einer zusätzlich dargestellten Einzelprognose zum Vergleich.

D: Die auf die Einzelprognose angewendete CRPS-Berechnung zeigt, dass, wenn der CRPS auf eine Einzelprognose angewendet wird, das Ergebnis eine MAE-Genauigkeitsmetrik ist. Tatsächlich sind Einzelprognosen triviale Formen probabilistischer Prognosen, bei denen wir implizit einer einzelnen Zahl eine 100%ige Wahrscheinlichkeit zuweisen. Anschließend wird ein kumulatives Wahrscheinlichkeitsdiagramm für den CRPS durch zwei Stufenfunktionen dargestellt – eine für Einzelprognosen und eine für die tatsächliche Nachfrage. Das bedeutet, dass je nach relativer Position der Einzelprognose zur tatsächlichen Nachfrage eine der beiden Summen in der CRPS-Formel (4) zu null wird: die erste Summe für Überprognosen und die zweite Summe für Unterprognosen.

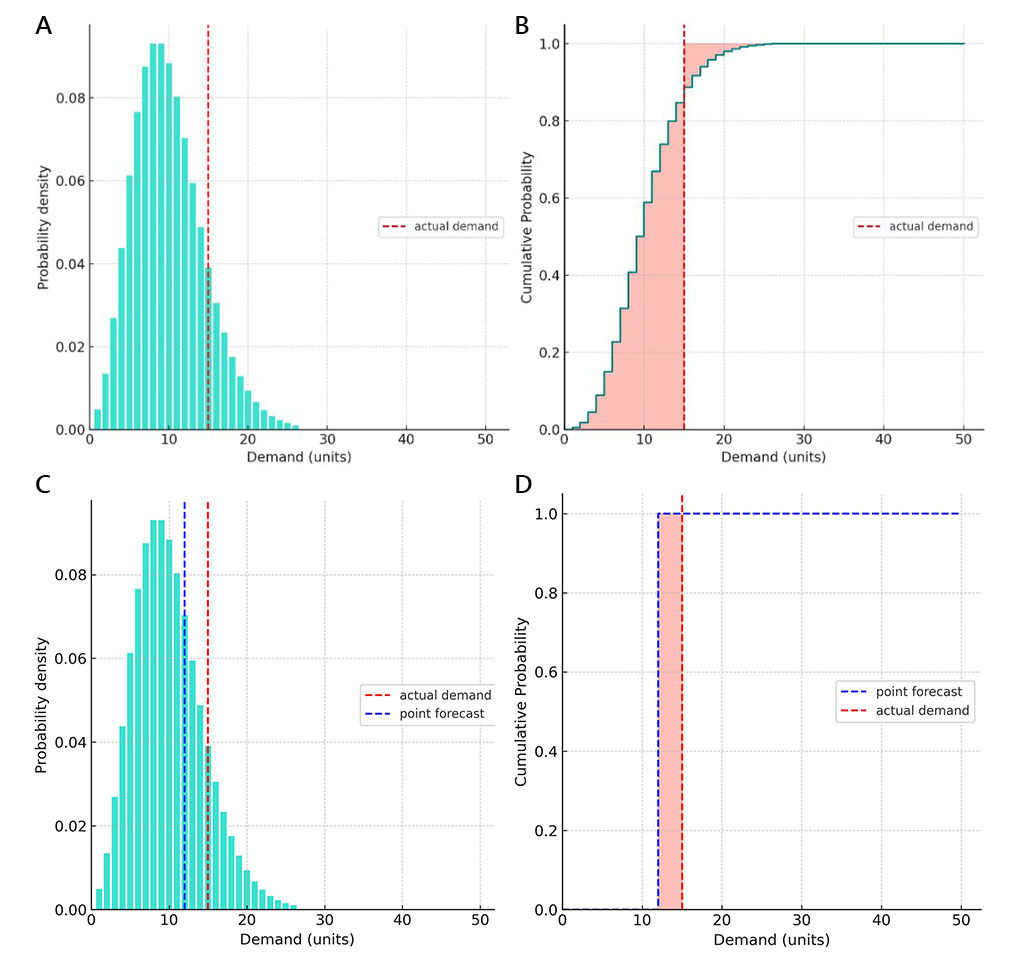
Ein Diagramm, das eine probabilistische Prognose und die CRPS-Metrik zur Bewertung ihrer Genauigkeit veranschaulicht.
A: Probabilistische Prognose. B: CRPS. C: Probabilistische vs. Einzelprognose. D: Der CRPS der Einzelprognose entspricht MAE.

Für das anhand dieser 4 Diagramme dargestellte Beispiel betragen die resultierenden CRPS-Werte für die probabilistische Prognose und für die Einzelprognose 3,32 bzw. 3. Betrachtet man die Zahlen, könnte man schließen, dass die Einzelprognose genauer ist, da ihre Genauigkeitsmetrik kleiner (besser) ist als die der probabilistischen Prognose. Diese Schlussfolgerung ist jedoch falsch.

Im obigen Beispiel haben wir nur einen Wert der tatsächlichen Nachfrage betrachtet, jedoch werden bei der Erstellung der probabilistischen Prognose unter Verwendung historischer Daten die Wahrscheinlichkeiten entsprechend den Auftretenshäufigkeiten der jeweiligen Nachfragewerte (unter Berücksichtigung der im Lerndatensatz verfügbaren Werte) angepasst. Werden sie angemessen gewählt, so wird der durchschnittliche CRPS-Wert für den Testdatensatz vergleichbar mit dem des Trainings-/Validierungsdatensatzes sein, da die Prognose die Auftretenshäufigkeiten unterschiedlicher Nachfragewerte in den Testdaten adäquat widerspiegelt.

Das unten stehende Diagramm veranschaulicht die Überlegenheit probabilistischer Prognosen gegenüber Einzelprognosen.

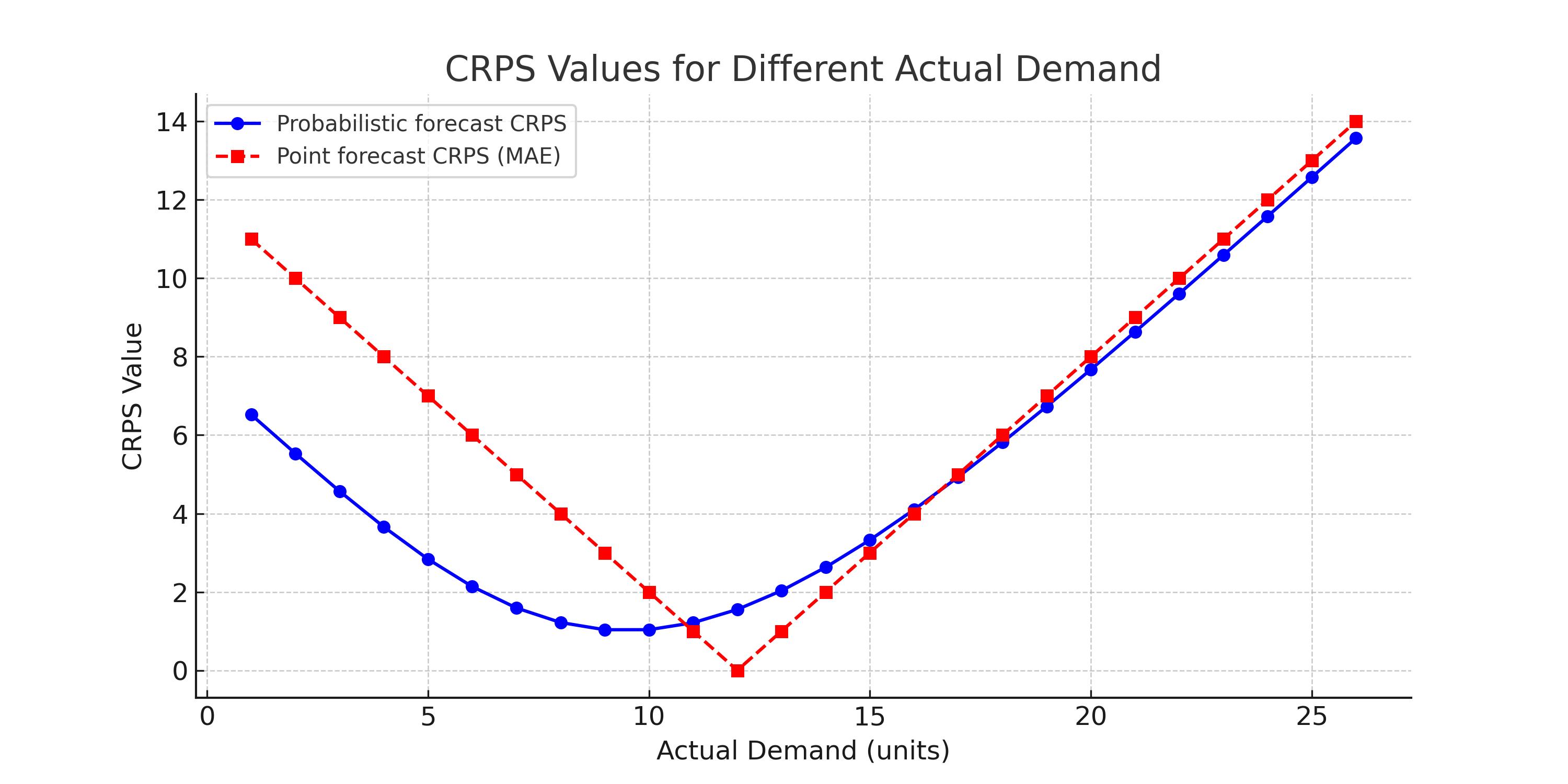
Ein Diagramm, das zeigt, wie sich der CRPS in Abhängigkeit von den tatsächlichen Werten sowohl für probabilistische als auch für Einzelprognosen ändert.

Beachten Sie, wie gleichmäßig sich der CRPS in Abhängigkeit von den unterschiedlichen tatsächlichen Werten verändert. Zudem ist festzustellen, dass abgesehen von einem winzigen Bereich (in dem die Einzelprognose der tatsächlichen Nachfrage sehr nahekommt), in allen anderen Bereichen der CRPS für probabilistische Prognosen kleiner ist als jener der Einzelprognose.

Würden wir mehrere unterschiedliche Einzelprognosen hätten, bliebe diese Beobachtung dennoch bestehen. Man müsste die rote Kurve je nach Einzelprognose gedanklich nach links oder rechts verschieben, aber die Überlegenheit probabilistischer Prognosen bliebe weiterhin gültig.

Literatur

Gneiting, T. und Raftery, A. E. (2004). Strictly proper scoring rules, prediction, and estimation. Technischer Bericht Nr. 463, Department of Statistics, University of Washington, Seattle, Washington, USA.