00:00 はじめに
02:55 リードタイムの事例
09:25 実際のリードタイム (1/3)
12:13 実際のリードタイム (2/3)
13:44 実際のリードタイム (3/3)
16:12 これまでの経緯
19:31 予定到着時間: 1時間後
22:16 CPRS (まとめ) (1/2)
23:44 CPRS (まとめ) (2/2)
24:52 クロスバリデーション (1/2)
27:00 クロスバリデーション (2/2)
27:40 リードタイムの平滑化 (1/2)
31:29 リードタイムの平滑化 (2/2)
40:51 リードタイムの構成 (1/2)
44:19 リードタイムの構成 (2/2)
47:52 準季節性リードタイム
54:45 対数ロジスティックリードタイムモデル (1/4)
57:03 対数ロジスティックリードタイムモデル (2/4)
01:00:08 対数ロジスティックリードタイムモデル (3/4)
01:03:22 対数ロジスティックリードタイムモデル (4/4)
01:05:12 不完全なリードタイムモデル (1/4)
01:08:04 不完全なリードタイムモデル (2/4)
01:09:30 不完全なリードタイムモデル (3/4)
01:11:38 不完全なリードタイムモデル (4/4)
01:14:33 リードタイムにおける需要 (1/3)
01:17:35 リードタイムにおける需要 (2/3)
01:24:49 リードタイムにおける需要 (3/3)
01:28:27 予測手法のモジュール性
01:31:22 結論
01:32:52 次回の講義と聴衆からの質問
説明
リードタイムは、ほとんどのサプライチェーンにおいて基本的な要素です。リードタイムは、需要と同様に予測可能であり、予測されるべきです。リードタイム専用の確率的予測モデルを使用することができます。サプライチェーンの目的のために確率的なリードタイム予測を作成する一連の技術が提示されます。これらの予測、すなわちリードタイムと需要の組み合わせは、サプライチェーンにおける予測モデリングの礎となります。
フル・トランスクリプト

このサプライチェーン講座シリーズへようこそ。私はジョアンネス・ヴェルモレルです。本日は「リードタイムの予測」について講演します。リードタイム、そして一般的にその他の遅延は、供給と需要のバランスを取る上でサプライチェーンの基本的な側面です。関係する遅延を考慮する必要があります。例えば、おもちゃの需要について考えてみましょう。クリスマス前の需要の季節的ピークを適切に予測しても、商品の受け取りが1月であれば意味がありません。リードタイムは、需要と同様に計画の細部を左右します。
リードタイムは変動します。非常に大きく変動するのです。これは事実であり、すぐにその証拠を示します。しかし、一見するとこの命題は不可解に思えます。そもそもなぜリードタイムがこんなにも変動するのかは明らかではありません。製造プロセスでは、1ミクロン未満の公差で動作することができます。さらに、製造プロセスの一環として、例えば光源の適用といった効果を1マイクロ秒単位で制御することが可能です。もし物質の変化をミクロン単位、そしてマイクロ秒単位で制御できるのなら、同程度の精度で需要の流れを制御できるはずです。あるいは、そうでないかもしれません。
この考え方は、なぜサプライチェーンの文献でリードタイムが軽視されがちであるかを説明するかもしれません。サプライチェーンの書籍や、結果として、サプライチェーンソフトウェアでは、在庫モデルの入力パラメーターとしてリードタイムを紹介する程度に、その存在がほとんど認められていません。本講義では、次の3つの目標があります:
リードタイムの重要性とその性質を理解したいと思います。 リードタイムを、特に不確実性を取り込むことができる確率的モデルに注目しながら、どのように予測できるかを理解したいと思います。 サプライチェーンの目的にかなう形で、リードタイム予測と需要予測を組み合わせる方法を見出したいと思います。

主流のサプライチェーン文献によれば、リードタイムは僅かな脚注程度の価値しかないとされています。この表現は誇張に聞こえるかもしれませんが、実際はそうではありません。科学文献に特化した検索エンジンであるGoogle Scholarによると、2021年の「demand forecasting(需要予測)」というクエリでは10,500本の論文がヒットします。結果をざっと見ると、実に大多数の論文があらゆる状況や市場における需要予測について論じていることがわかります。同じく2021年でGoogle Scholarで「lead time forecasting(リードタイム予測)」というクエリを実行すると、結果は71件にとどまります。リードタイム予測に関する論文の件数は非常に限られており、1年分の研究を概観するのも数分で済むほどです。
実際、リードタイムの予測について真に論じているのはせいぜい十数件であることが判明しています。実際には、「long lead time forecast(長いリードタイム予測)」や「short lead time forecast(短いリードタイム予測)」といった表現で、需要予測を指している場合がほとんどで、リードタイムそのものの予測を指しているわけではありません。この演習は、「demand prediction(需要予測)」や「lead time prediction(リードタイム予測)」など、類似の表現や他の年に対しても繰り返すことが可能です。それらのバリエーションも同様の結果をもたらします。これは聴衆の皆さんへの課題として残しておきます。
この概算から、需要予測に関する論文はリードタイム予測に関する論文の約1,000倍存在するといえます。サプライチェーンの書籍やソフトウェアもこれに倣い、リードタイムは二流の存在、取るに足らない技術的な側面として扱われています。しかし、本講義シリーズで紹介するサプライチェーンの関係者は、異なる見解を示します。これらの関係者は架空の企業を代表しているかもしれませんが、サプライチェーンの典型的なアーキタイプを反映しています。彼らは、典型的な状況とはどのようなものかを示してくれます。では、リードタイムに関して彼らが何を伝えてくれるか見てみましょう。
Parisは、自社の小売ネットワークを展開する架空のファッションブランドです。Parisは海外のサプライヤーから注文を行い、リードタイムは長く、時には6ヶ月以上に及ぶこともあります。これらのリードタイムは不完全にしか把握されていませんが、新作コレクションは、関連するマーケティング活動で定義された適切なタイミングで店舗に投入されなければなりません。サプライヤーのリードタイムは、適切な予測を必要とします;つまり、予測が必要です。
Amsterdamは、チーズ、クリーム、バターの製造に特化した架空のFMCG企業です。チーズの熟成プロセスは既知で制御されていますが、数日程度の変動があります。しかし、その数日間こそが、Amsterdamの主要な販売チャネルである小売チェーンによって引き起こされる集中的なプロモーションの期間に他なりません。これらの製造リードタイムは予測を必要とします。
Miamiは、架空の航空 MRO(メンテナンス、修理、オーバーホール)企業です。MROは、メンテナンス、修理、オーバーホールの略です。全てのジェット機は飛行を継続するために年間で数千点の部品を必要とします。一つの部品の不足が航空機を離陸不能にする可能性があります。修理可能な部品の修理期間、すなわちTAT(ターンアラウンドタイム)は、回転部品が再び使用可能になる時期を定義します。しかし、このTATは修理の内容に応じて日から月単位まで変動し、部品が航空機から取り外された時点ではその修理内容は分かっていません。これらのTATは予測を必要とします。
San Joseは、多種多様な家庭用品やアクセサリーを流通させる架空のeコマース企業です。サービスの一環として、San Joseは各取引に対して納期の約束を行っています。しかし、実際の配送は信頼性が完全とは言えない第三者の企業に依存しています。したがって、San Joseは各取引に対して約束できる納期について十分な見積もりを必要とします。この見積もりは暗黙のうちにリードタイム予測であると言えます。
最後に、Stuttgartは架空の自動車アフターマーケット企業です。同社は、自動車修理を提供する支店を運営しています。自動車部品の最低購入価格は、長くやや不規則なリードタイムを提供する卸売業者から得ることができます。一方、より信頼性が高いが、価格が高く、距離が近いサプライヤーも存在します。各部品に対して適切なサプライヤーを選択するには、各サプライヤーに関連するリードタイムの適切な比較分析が必要です。
ご覧の通り、ここまでに紹介したすべてのサプライチェーン関係者は、少なくとも1つ、しばしば複数のリードタイムの予測を必要としています。需要予測の方がリードタイム予測よりも注意と労力を要すると議論することもできますが、最終的にはほとんどすべてのサプライチェーン状況で両方が必要とされます。
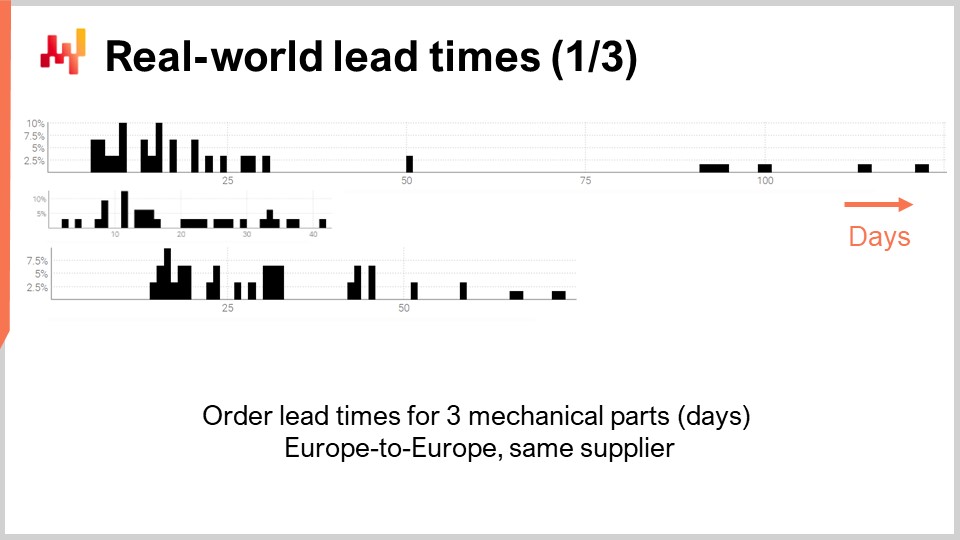
では、いくつかの実際のリードタイムを見てみましょう。画面には、3種類の機械部品に関連する観測されたリードタイムを集計して作成された3つのヒストグラムが表示されています。これらの部品は、西ヨーロッパに所在する同じサプライヤーから注文されたものです。注文は同じく西ヨーロッパに所在する企業から行われています。x軸は観測されたリードタイムの期間(日数で表される)を示し、y軸は観測数をパーセンテージで示しています。以下、すべてのヒストグラムは同じ規則に従い、x軸は日数、y軸は頻度を表します。これら3つの分布から、いくつかの観察結果を得ることができます。
まず、データがまばらであることが挙げられます。観測値は数十件に過ぎず、これらのデータは数年にわたって収集されたものです。この状況は典型的です。もし企業が月に一度だけ注文するなら、リードタイムの観測値100件を集めるのにほぼ10年かかります。したがって、統計処理を行うにあたっても、大規模な数値ではなく、小規模な数値に対応する必要があります。実際、大量のデータを扱える贅沢さはなかなか得られないでしょう。
第二に、リードタイムは不規則です。観測値は数日から四半期に及ぶまで幅があります。平均リードタイムを算出することは可能ですが、どの部品に対しても平均値に依存するのは賢明とは言えません。また、これらの分布が正規分布に近いものではないことも明らかです。
第三に、サイズや価格が比較的似通った3種類の部品が存在するにもかかわらず、リードタイムは大きく変動します。データをより充実させるためにこれらの観測値をまとめてしまいたくなるかもしれませんが、非常に異なる分布を混ぜ合わせることになるため、明らかに賢明ではありません。これらの分布は、平均や中央値、さらには最小値や最大値においても一致していません。
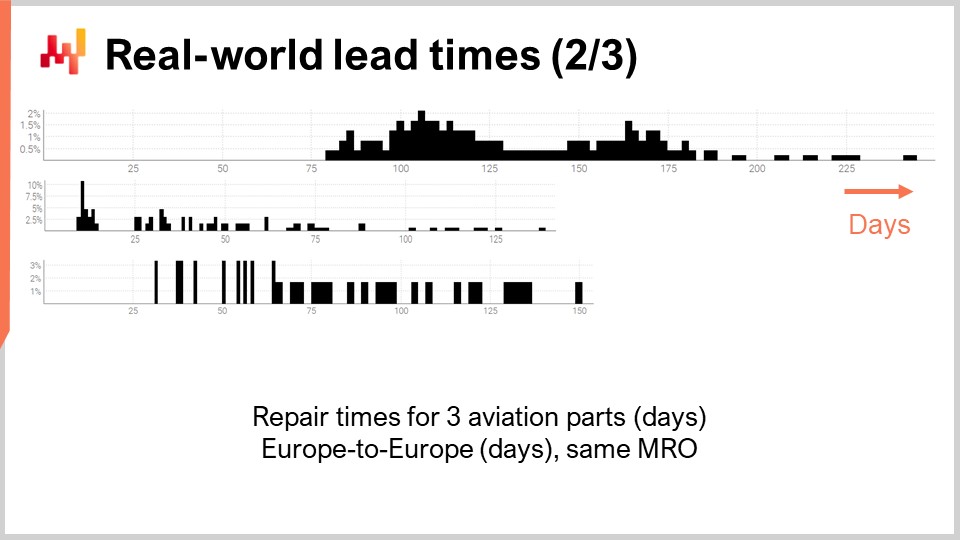
次に、別のリードタイムの群を見てみましょう。これらの期間は、3つの異なる航空機部品の修理に要する時間を反映しています。最初の分布は、2つのモードと尾部があるように見えます。分布に2つのモードが現れる場合、通常それはそれらのモードを説明する隠れた変数が存在することを示唆します。例えば、2種類の異なる修理作業が存在し、それぞれ固有のリードタイムがある可能性があります。2番目の分布は、1つのモードと尾部があるように見えます。このモードは約2週間という比較的短い期間に一致します。これは、部品がまず検査され、場合によっては追加の介入なしに使用可能と判断されるプロセスを反映している可能性があり、その結果、リードタイムが大幅に短縮されるのです。3番目の分布は、明確なモードや尾部が見られず、全体に広がっているように見えます。ここでは複数の修理プロセスが混在している可能性があり、それらがひとまとめになっているかもしれません。観測点がたった36件ほどと少ないため、これ以上詳しく断言するのは難しいです。この3番目の分布については、本講義の後半で再検討します。
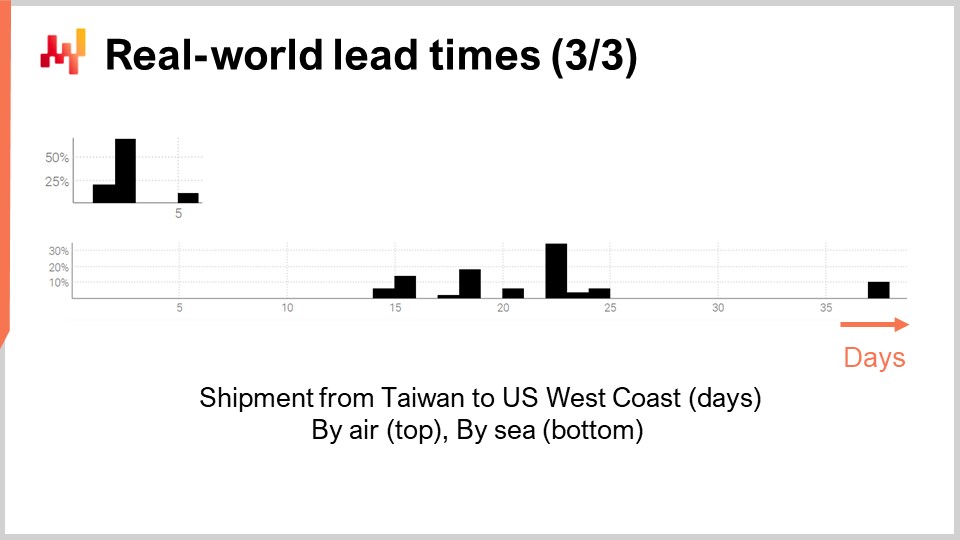
最後に、台湾から米国西海岸への輸送遅延を表す2つのリードタイムを見てみましょう。航空輸送と海上輸送のいずれの場合も、予想通り貨物機は貨物船よりも速いです。2番目の分布は、海上輸送の場合、元の船に間に合わず、次の船で出荷されることで、遅延がほぼ倍増する可能性を示唆しているようです。同じ現象が航空輸送にも見られるかもしれませんが、データが非常に限られているため、あくまで推測に過ぎません。ここで指摘しておきたいのは、リードタイムに関しては、数件の観測値しか得られないという状況は珍しいことではないという点です。こうした状況は頻繁に起こります。本講義では、数千件もの観測値ではなく、手元にあるごくわずかなリードタイムデータを活用できるツールや手法を探求していることを念頭に置くことが重要です。両分布における短い隙間は、曜日ごとの周期性が働いていることも示唆していますが、現在のヒストグラムではこの仮説を検証するには適切ではありません。
実際のリードタイムに関するこの短いレビューから、背後にあるいくつかの現象を把握することができます。確かに、リードタイムは高度に構造化されており、遅延は原因なしに発生することはなく、それらの原因は特定、分解、定量化することが可能です。しかし、リードタイムの細部の構成は、少なくとも現時点では、ITシステムに十分に記録されていないことが多いです。航空業界のような特定の産業で観測されたリードタイムの詳細な分解が利用可能であっても、リードタイムが完全に予測可能であることを意味するわけではありません。リードタイム内のサブセグメントや各フェーズは、それぞれ固有の不可避な不確実性を示す可能性があります。
このサプライチェーン講義シリーズは、サプライチェーンの研究と実践の両面に関する私の見解と洞察を示しています。これらの講義をある程度独立させようとしていますが、連続して視聴する方が理解が深まります。本講義の残りは、このシリーズで既に紹介された要素に依存していますが、すぐに復習を行います。
最初の章は、サプライチェーンの分野およびその研究に関する一般的な紹介です。この講義シリーズで採用される視点を明らかにします。すでにお気づきかもしれませんが、この視点はサプライチェーンに関して一般的に考えられている主流のものとは大きく異なります。
第2章では、一連の方法論を紹介します。実際、サプライチェーンは素朴な方法論を打ち破ります。サプライチェーンは、それぞれ独自の目的を持つ人々で構成されているため、中立的な存在は存在しません。この章では、予測 供給チェーン最適化を専門とする企業向けソフトウェア会社LokadのCEOとしての私自身の利害の衝突を含む、これらの複雑な点に対処します。
第3章では、一連のサプライチェーン「ペルソナ」を概観します。これらのペルソナは、今日簡単にレビューした架空の企業であり、サプライチェーンの状況の原型を表すことを意図しています。これらのペルソナの目的は、解決策の提示を後回しにして、問題に専念することにあります。
第4章では、サプライチェーンの補助科学について見直します。これらの科学はサプライチェーンそのものに関するものではありませんが、現代のサプライチェーン実践には不可欠と考えられるべきです。この章では、コンピューティングハードウェアからサイバーセキュリティの懸念に至るまで、抽象化層を通った進行が含まれます。
第5章、そして本章は予測モデリングに専念しています。予測モデリングは単なる需要予測よりも一般的な視点であり、単に需要を予測するだけのものではありません。これは、関心のあるサプライチェーンの将来の要因を推定し、定量化するために使用できるモデルの設計に関するものです。今回はリードタイムに焦点を当てますが、より広くサプライチェーンでは、ある程度の確実性をもって知られていないものには全て予測が必要です。
第6章では、予測モデル、より具体的には第5章で紹介した確率モデルを活用しながら最適化された意思決定をどのように計算するかを説明します。第7章では、量的供給チェーンマニフェストの取り組みの実際の企業実行について議論するため、主に非技術的な視点に戻ります。

本日はリードタイムに焦点を当てます。リードタイムがなぜ重要であるかを見たばかりで、実際のリードタイムの短い一連の例をレビューしたばかりです。したがって、リードタイムモデリングの要素に進みます。確率論的な視点を採用するため、確率予測の良さを評価する指標であるContinuous Rank Probability Score (CRPS)を簡単に再紹介します。また、クロスバリデーションと、確率論的視点に適したクロスバリデーションの変種も紹介します。これらのツールを用いて、リードタイムに関する初の非ナイーブな確率モデルを紹介し評価します。リードタイムのデータはまばらであるため、最初の課題はこれらの分布を平滑化することです。リードタイムは一連の中間フェーズに分解することができるので、分解されたリードタイムのデータが利用できると仮定すると、確率論的な視点を維持しながらそれらを再構成する何かが必要です。
次に、差分可能プログラミングを再紹介します。差分可能プログラミングは、この講義シリーズですでに需要予測に使われましたが、リードタイム予測にも利用できます。アジアからの輸入品に見られる典型的なパターンである旧正月がリードタイムに与える影響を捉えるためのシンプルな例から始めます。
次に、対数ロジスティック分布を活用したリードタイムのパラメトリックな確率モデルに進みます。改めて、差分可能プログラミングがモデルのパラメータ学習において重要な役割を果たします。その後、不完全なリードタイムの観測値を考慮してこのモデルを拡張します。実際、まだ完了していない発注であっても、リードタイムに関する情報が得られます。
最後に、単一の在庫補充状況において、確率的なリードタイム予測と確率的な需要予測を統合します。これにより、予測モデリングにおいてモジュール性が、モデル自体の細部以上に重要である理由を実証する機会となります。

確率予測に関する講義5.2では、すでに確率予測の質を評価するためのいくつかのツールを紹介しています。実際、平均二乗誤差や平均絶対誤差といった一般的な精度指標は点予測にのみ適用され、確率予測には適用されません。しかし、予測が確率的になったからといって、一般的な意味での精度が無視されるわけではありません。確率論的な視点に適合する統計的な手段が必要なだけなのです。
これらの手段の中に、Continuous Rank Probability Score (CRPS)があります。画面にはその式が示されています。CRPSは、L1メトリック、すなわち絶対誤差の確率分布版の一般化です。一般的なCRPSは、ここでFと呼ばれる分布と、Xと呼ばれる観測値を比較します。CRPS関数から得られる値は観測値と同一の単位で表されます。例えば、Xが日数で表されたリードタイムであれば、CRPSの値も日数で表されます。

CRPSは、2つの分布を比較するためにも一般化することができます。画面で行われているのはこのことです。これは先の式のわずかな変形にすぎません。この指標の本質は変わらないのです。もしFが真のリードタイム分布で、F_hatがその推定値であれば、CRPSは日数で表されます。CRPSは、2つの分布間の違いの大きさを反映します。また、CRPSは、最初の分布から全ての質量を移動させ、第二の分布と全く同じ形にするのに必要な最小限のエネルギーとして解釈することもできます。
これで、一次元の2つの確率分布を比較する手段が整いました。これは、まもなくリードタイムの初の確率モデルを導入する際に重要となるでしょう。
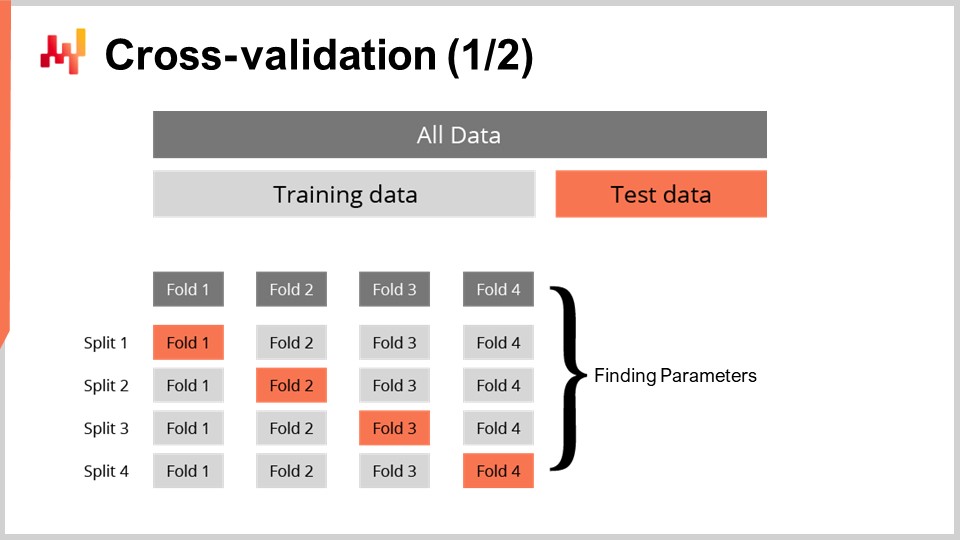
確率予測の良さを測る指標があるだけでは十分ではありません。その指標は手元にあるデータでの良さを測るものですが、我々が真に求めているのは、まだ存在しないデータに対して予測の良さを評価する能力です。実際、我々が関心を持つのは過去に観測されたリードタイムではなく、未来のリードタイムなのです。我々のモデルが未観測のデータに対して良い性能を発揮する能力を、一般化能力と呼びます。クロスバリデーションは、まさにモデルの一般化能力を評価するための一般的な手法です。
最も単純な形では、クロスバリデーションは観測値を少数のサブセットに分割することから成り立ちます。各反復で、一つのサブセットが取り除かれ、テストサブセットと呼ばれます。そして、残りのサブセット(トレーニングサブセットと呼ばれる)を用いてモデルが生成または訓練されます。訓練後、モデルはテストサブセットに対して検証されます。このプロセスは何度か繰り返され、すべての反復で得られた平均的な良さが最終的なクロスバリデーション結果となります。
観測値間の時間依存性のため、時系列予測の文脈ではクロスバリデーションはほとんど使用されません。先に述べたように、クロスバリデーションは観測値が独立していることを前提としています。時系列の場合は、代わりにバックテストが使用されます。バックテストは、時間依存性を考慮に入れたクロスバリデーションの一形態と見なすことができます。
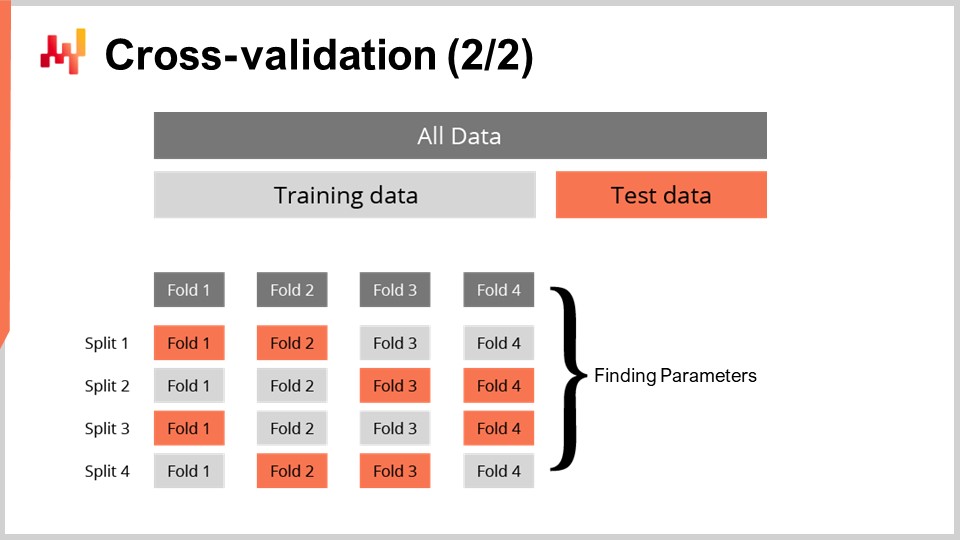
クロスバリデーションの手法には、対処すべき多くの側面を反映する無数のバリエーションがありますが、本講義の目的のためにそれらをすべて網羅することはありません。私は、各分割でトレーニングサブセットとテストサブセットがおおよそ同じサイズになる特定のバリエーションを使用します。この方法は、まもなくコードで示すように、確率モデルの検証に対応するために導入されたものです。
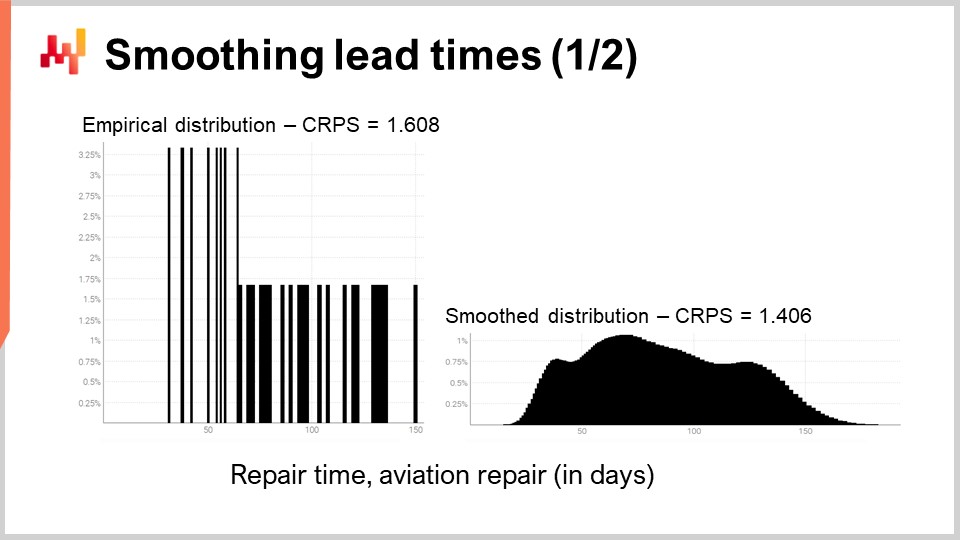
以前画面で見た実際のリードタイムの一例を再び見てみましょう。左側では、ヒストグラムが第3の航空機修理時間分布に関連付けられています。これらは先ほど見た観測値と同じもので、ヒストグラムは単に縦方向に引き伸ばされただけです。これにより、左右のヒストグラムは同じスケールを共有します。左側のヒストグラムでは約30件の観測値があります。それほど多くはありませんが、通常得られる数よりは多いのです。
左側のヒストグラムは実証的分布と呼ばれます。これは観測値から得られた生のヒストグラムそのものです。ヒストグラムは、整数日で表される各期間に対して1つのビンを持ち、各ビンごとに観測されたリードタイムの数をカウントしています。データがまばらなため、実証的分布はバーコードのように見えます。
ここに問題があります。もし、ちょうど50日で2件のリードタイムが観測されている場合、49日や51日が観測される確率が全くゼロであると言えるでしょうか?それはありえません。明らかに、連続した期間の幅が存在するにもかかわらず、実際の基礎分布を観測するのに十分なデータがないだけであり、その基礎分布はこのバーコードのような分布よりもはるかに滑らかであるはずです。
したがって、この分布を平滑化する方法は無数にあります。見た目は良くても統計的に妥当でない平滑化手法も存在します。良い出発点として、平滑なモデルが実証的分布よりもより正確であることを確認したいと考えています。実は、CRPSとクロスバリデーションという2つの手段を既に導入しており、それによってそれが可能となるのです。
すぐに、結果が表示されます。バーコード分布に関連するCRPS誤差は1.6日であり、平滑な分布に関連するCRPS誤差は1.4日です。これらの数値はクロスバリデーションによって得られました。誤差が低いということは、CRPSの観点から見て、右側の分布が2つの中で最も正確であることを示しています。1.4日と1.6日の差0.2日は大きな差ではありませんが、ここで重要なのは、いくつかの中間期間が突発的にゼロ確率になることなく滑らかに分布している点です。これは合理的であり、修理プロセスの理解から、修理が繰り返されればその期間はほぼ必ず発生するはずだと考えられるためです。CRPSは、この平滑化によってもたらされた改善の真の深さを反映しているわけではありませんが、少なくともCRPSが低下したことで、この変換が統計的に妥当であることが確認されます。
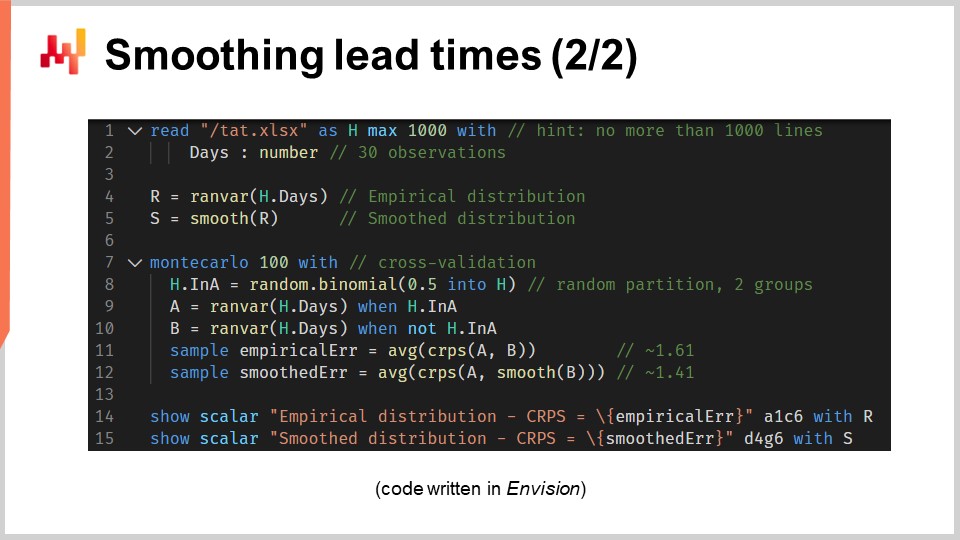
それでは、これら2つのモデルを生成し、2つのヒストグラムを表示したソースコードを見てみましょう。空行を除けば、全体で12行のコードで実現されています。いつものように、この講義シリーズでは、サプライチェーンの予測最適化のためにLokadが開発したドメイン固有言語Envisionでコードが書かれています。しかし、魔法のようなものではなく、このロジックはPythonで書くことも可能です。ただし、本講義で扱う問題に関しては、Envisionの方がより簡潔で自己完結しています。
これらの12行のコードを見直してみましょう。1行目と2行目では、データが1列のみのExcel スプレッドシートを読み込んでいます。このスプレッドシートには30件の観測値が含まれており、これらのデータは「days」という1列のみを持つ"H"という名前のテーブルにまとめられています。4行目では、実証的分布を構築しています。変数"R"はデータ型"ranvar"を持っており、代入の右側にある"ranvar"関数は、観測値を入力として受け取り、“ranvar"データ型で表現されたヒストグラムを返す集約関数です。その結果、“ranvar"データ型は一次元の整数分布に特化しています。“ranvar"データ型はこの章の前の講義で紹介しました。このデータ型は、各操作に対して一定のメモリ使用量と一定の計算時間を保証します。ただし、“ranvar"の欠点は、不可逆的な圧縮が伴う点ですが、その圧縮によるデータ損失はサプライチェーンの目的において無視できるよう設計されています。
5行目では、組み込み関数 “smooth” を使って分布を平滑化しています。内部的には、この関数は元の分布をポアソン分布の混合に置き換えます。ヒストグラムの各ビンは、そのビンの整数位置と等しい平均値を持つポアソン分布に変換され、最終的に混合は各ポアソン分布に、そのビン自体の重みに比例した重みを割り当てます。別の見方をすれば、“smooth” 関数は、各観測値をそれ自体と等しい平均値を持つポアソン分布に置き換えるのと同等であり、その後、各観測値ごとのポアソン分布が混合されます。混合とは、各ヒストグラムビンの値を平均化することを意味します。なお、“ranvar"変数"R"と"S"は、14行目と15行目で表示されるまで再利用されません。
7行目では、モンテカルロブロックを開始します。このブロックは一種のループであり、モンテカルロというキーワードの直後にある100という値によって100回実行されます。モンテカルロブロックは、ある程度のランダム性を含むプロセスに従って生成される独立した観測値を収集するためのものです。一般的なプログラミング言語で通常用いられるループではなく、なぜEnvisionに特定のモンテカルロ構文があるのかと疑問に思われるかもしれませんが、専用の構文を持つことで大きな利点が得られるのです。まず、疑似乱数生成に使用されるシードに至るまで、各反復が真に独立していることが保証されます。次に、複数のCPUコアまたは複数のマシンに対して作業負荷を自動的に分散する明確なターゲットを提供します。
8行目では、テーブル “H” 内にブール値のランダムベクトルを作成します。この行では、テーブル “H” の各行ごとに、真または偽の独立したランダムな値(偏差値)を生成しています。Envisionでは通常、ループが配列プログラミングにより抽象化されています。これらのブール値を用いて、テーブル “H” を2つのグループに分割しています。このランダムな分割は交差検証プロセスに利用されます.
9行目と10行目では、それぞれ “A” と “B” という2つの “ranvar” を作成しています。再び “ranvar” 集約関数を使用していますが、今回は集約関数呼び出し直後に “when” キーワードでフィルターが適用されています。“A” は、変数 a の値が true である行のみを用いて生成され、“B” はその逆、すなわち a の値が false である行のみから生成されます.
11行目と12行目では、モンテカルロブロックから注目すべき数値を収集しています。Envisionでは、キーワード “sample” はモンテカルロブロック内にのみ配置可能で、モンテカルロプロセスを何度も反復する際に行われる観測値を収集するために使用されます。11行目では、元のリードタイム集合からのサブサンプルという2つの経験的分布間のCRPSで表される平均誤差を計算しています。“sample” キーワードは、モンテカルロ反復中に収集された値を指定しており、右辺にある “AVG” 集約関数(平均を意味)は、ブロック終了時に単一の推定値を生成するために用いられます.
12行目では、11行目で行った操作とほぼ同じことを実行します。ただし今回は、“ranvar” “B” に対して “smooth” 関数を適用します。スムース版が単純な経験的分布とどれだけ近いかを評価したいのです。結果として、CRPSの観点からは元の経験的分布よりも近いことが分かりました.
14行目と15行目では、ヒストグラムとCRPSの値を表示します。これらの行は、前のスライドで見た図を生成しています。このスクリプトは、モデルの経験的分布の品質に対するベースラインを示すものです。実際、この “barcode” モデルは一見単純に見えるものの、確率的なモデルであることに変わりはなく、なおかつ確率論的な側面を持っています。したがって、このスクリプトは、少なくともCRPSの観点からは、元の経験的分布のスムース版を通じてより良いモデルも提供しています.
現時点では、プログラミング言語にどれだけ精通しているかによっては、非常に多くの情報に圧倒されるように感じるかもしれません。しかしながら、観測数がわずかでも合理的な確率分布を作成できることは、非常にシンプルであると強調したいと思います。コードは12行ありますが、実際のモデリング部分は4行目と5行目のみです。もしスムース版のみに興味があるなら、“ranvar” “S” は1行のコードで済むでしょう。つまり、まず ranvar 集約を適用し、次にスムーズ演算子を適用するだけで完了する、文字通りワンライナーのコードです。残りは単なる計測と表示であり、適切なツールがあれば、リードタイムであれ他の何であれ、確率的モデリングは極めてシンプルに行えます。大掛かりな数学も、複雑なアルゴリズムも、巨大なソフトウェアも必要ありません。それは単純で、驚くほどシンプルなのです.

どのようにして出荷が6ヶ月遅れるのでしょうか?答えは明白です:一日ずつ進むのです。より真面目に言えば、リードタイムは通常、一連の遅延に分解できます。例えば、サプライヤのリードタイムは、注文がバックログキューに入る際の待機遅延、商品が製造される際の製造遅延、そして最終的に商品が出荷される際の輸送遅延に分解することができます。したがって、リードタイムが分解可能であるならば、それを再構成できることも重要です.
もし未来が正確に予測できる非常に決定論的な世界に生きていたならば、リードタイムの再構成は単なる加算の問題に過ぎなかったでしょう。先ほどの例に戻ると、注文リードタイムは、待機遅延(日数)、製造遅延(日数)、および輸送遅延(日数)の合計となります。しかし、我々は未来が完全に予測可能な世界には存在しません。今回の講義冒頭で示した現実のリードタイム分布は、この命題を裏付けるものです。リードタイムは不規則であり、今後数十年にわたって根本的に変わる理由はほとんどありません.
したがって、将来のリードタイムはランダム変数として扱うべきです。これらのランダム変数は、不確実性を無視するのではなく、取り込み、定量化します。具体的には、リードタイムの各構成要素も個別にランダム変数としてモデル化する必要があります。先ほどの例に戻ると、注文リードタイムはランダム変数であり、待機遅延、製造遅延、輸送遅延という3つのランダム変数の合計として得られるのです.
画面には、独立した一次元の整数値ランダム変数2つの和の公式が示されています。この公式は、もし合計がZ日であり、最初のランダム変数XがK日を占めるならば、2番目のランダム変数YはZ-K日でなければならないと述べています。この種の加算は、一般に数学では畳み込みと呼ばれています.
一見、この畳み込みには無限の項が存在するように思われるかもしれませんが、実際には有限の項のみを考慮すれば十分です。まず、すべての負の期間は確率がゼロであり、負の遅延は時間を逆行することを意味するからです。次に、大きな遅延の場合、確率が極めて小さくなるため、実用的なサプライチェーン上ではほぼゼロと見なすことができます.
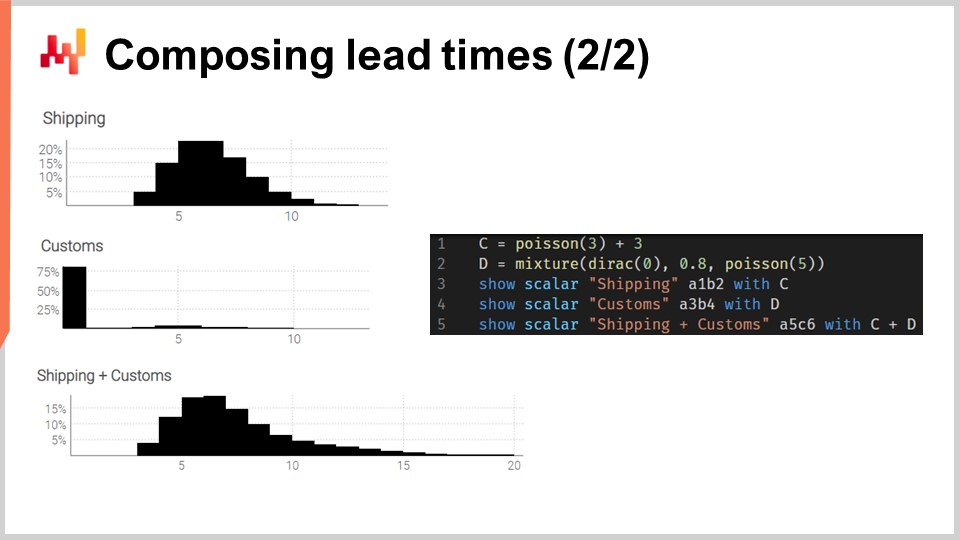
これらの畳み込みを実際に適用してみましょう。まず、出荷遅延と通関での遅延という2つのフェーズに分解できる輸送時間を考察します。この2つのフェーズを独立した2つのランダム変数でモデル化し、それらを加算して輸送時間を再構成したいのです.
画面の左側に表示されるヒストグラムは、右側のスクリプトによって生成されています。1行目では、出荷遅延が定数を加えたポアソン分布の畳み込みとしてモデル化されています。ポアソン関数は “ranvar” データ型を返し、3を加えることで分布が右にシフトします。結果として得られた “ranvar” は変数 “C” に代入され、3行目で表示されます。これは、数単位(この場合は3単位)右にシフトしたポアソン分布の形状として確認できます。2行目では、税関での通関がゼロにおけるディラック分布と5におけるポアソン分布の混合としてモデル化されています。ゼロにおけるディラック分布は全体の80%の確率で現れ、これは多くの場合、貨物が税関で検査されずに特に遅延なく通過する状況を反映しています。一方、20%の場合、貨物は税関で検査され、遅延は平均5のポアソン分布としてモデル化されます。結果として得られた ranvar は変数 “D” に代入され、4行目で表示され、左側の中央部のヒストグラムとして示されます。この非対称な特性は、ほとんどの場合、税関が追加の遅延を引き起こさないことを反映しています.
最後に、5行目で C と D の和を計算します。この加算は、C と D の両方が数値ではなく ranvar であるため、畳み込みとなります。これは、このスクリプト内で2回目の畳み込みが行われたことを意味します(既に1行目で畳み込みが実行されています)。結果として得られた ranvar は表示され、左側の3番目で最下部のヒストグラムとして示されます。この3番目のヒストグラムは最初のものと似ていますが、尾部がはるかに右に広がっているのが特徴です。再び、数行のコードで、通関での遅延のような現実の非自明な効果に対応できることが示されました.
しかし、この例には2つの批判があるかもしれません。第一に、定数がどこから来るのかが明示されていないことです。実際には、これらの定数を歴史的なデータから学習したいのです。第二に、ポアソン分布はシンプルであるという利点はあるものの、特に裾が重い状況を考えると、リードタイムのモデリングにおいて必ずしも現実的な形状とは言えないかもしれません。そこで、これら2点について対処する必要があります.
データからパラメータを学習するために、このシリーズの講義で既に紹介したプログラミングパラダイム、すなわち微分可能プログラミングに立ち返ります。もしこの章の以前の講義をまだ視聴していないなら、現講義終了後にぜひご覧いただきたいと思います。微分可能プログラミングについては、これらの講義でさらに詳しく紹介されています.
微分可能プログラミングは、確率的勾配降下法と自動微分という2つの技術の組み合わせです。確率的勾配降下法は、各観測値ごとにパラメータを勾配の逆方向へ微調整する最適化手法であり、自動微分は、プログラミング言語のコンパイラのように、一般的なプログラム内に現れる全パラメータの勾配を計算するコンパイル技術です.
リードタイムの問題を例に、微分可能プログラミングを説明しましょう。これは、このパラダイムに精通しているかどうかにかかわらず、復習または入門として役立つでしょう。ここでは、中国からの輸入に関連するリードタイムにおける旧正月の影響をモデル化しようとしています。実際、旧正月のために工場が2~3週間閉鎖されるため、リードタイムが延びるのです。旧正月は周期的に毎年訪れますが、グレゴリオ暦における厳密な季節性を持つわけではありません.
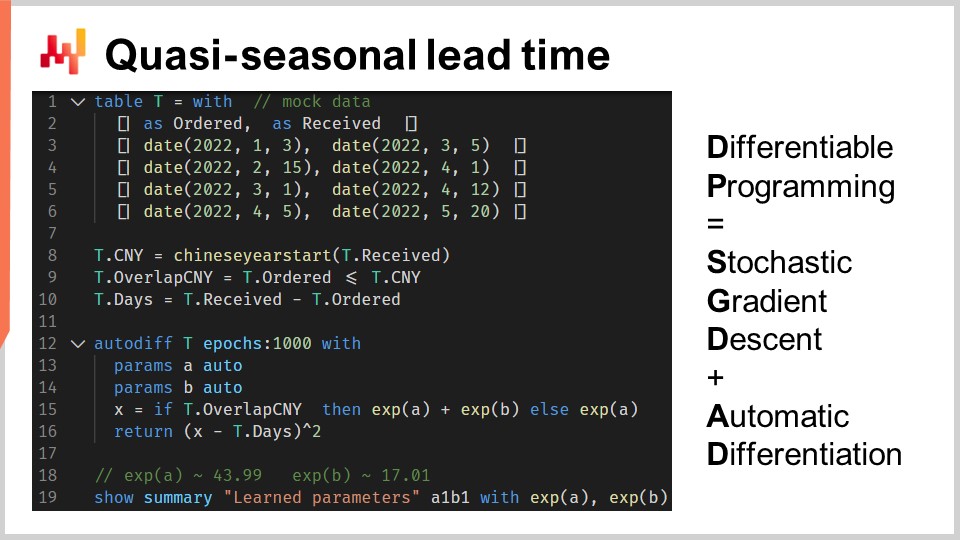
1行目から6行目では、注文日と受取日を含む4件の架空の購入注文を導入しています。実際、これらのデータはハードコードされるのではなく、企業のシステムから過去のデータとして読み込まれるでしょう。8行目と9行目では、リードタイムが旧正月と重なるかどうかを計算しています。変数 T.overlap_CNY はブール値のベクトルで、観測値が旧正月の影響を受けるか否かを示しています.
12行目では “autodiff” ブロックを導入します。テーブル T が観測テーブルとして使用され、1000 エポックが設定されています。これは、テーブル T の各観測値、つまり各行が1000回訪問されることを意味します。確率的勾配降下法の1ステップは、“autodiff” ブロック内のロジックの1回の実行に対応します.
13行目と14行目では、2つのスカラー・パラメータが宣言されます。“autodiff” ブロックはこれらのパラメータを学習します。パラメータ A は旧正月の影響がない場合のベースラインリードタイムを、パラメータ B は旧正月に起因する追加遅延をそれぞれ反映します。15行目では、モデルのリードタイム予測である X を計算します。これは決定論的モデルであり、確率的なものではありません。つまり、X は一点のリードタイム予測を示します。右辺は単純で、もし観測値が旧正月と重なれば、ベースラインに旧正月の要素を加えた値を返し、そうでなければベースラインのみを返します。“autodiff” ブロックは各観測値ごとに処理するため、15行目での T.overlap_CNY はベクトルではなくスカラー値となります。この値は、テーブル T 内で観測値として選ばれた1行と一致します.
パラメータ A と B は、微分可能プログラミングの小技である指数関数 “exp” に包み込まれています。実際、確率的勾配降下法を操るアルゴリズムは、パラメータの増分変化に対して比較的保守的であるため、もし10以上に成長する可能性のある正のパラメータを学習したい場合、このパラメータを指数関数で処理することで収束が促進されます.
16行目では、予測 X と観測された期間(T.days で日数として表現)との間の平均二乗誤差を返します。再び、“autodiff” ブロック内では T.days はスカラー値となり、テーブル T が観測テーブルとして扱われるため、この返り値は確率的勾配降下法によって最小化される損失として扱われます。自動微分は、この損失からパラメータ A と B への勾配を逆伝播させます。最後に、19行目で、リードタイムのベースラインと旧正月成分に対応する学習済みのパラメータ A と B の値が表示されます.
これで、統計的パターンを学習する多用途なツールとしての微分可能プログラミングの再紹介を終了します。ここから、より複雑な状況に合わせた “autodiff” ブロックの再検討に入ります。しかし、たとえ少々圧倒されるように感じても、ここで行われている処理は決して複雑なものではないことを改めて強調しておきます。おそらく、このスクリプトで最も複雑なコードは、8行目で呼ばれる “ChineseYearStart” 関数の実装部分であり、これは Envision 標準ライブラリの一部です。数行のコードで、2つのパラメータを持つモデルを導入し、それらのパラメータを学習するというシンプルさは、実に驚くべきものです.
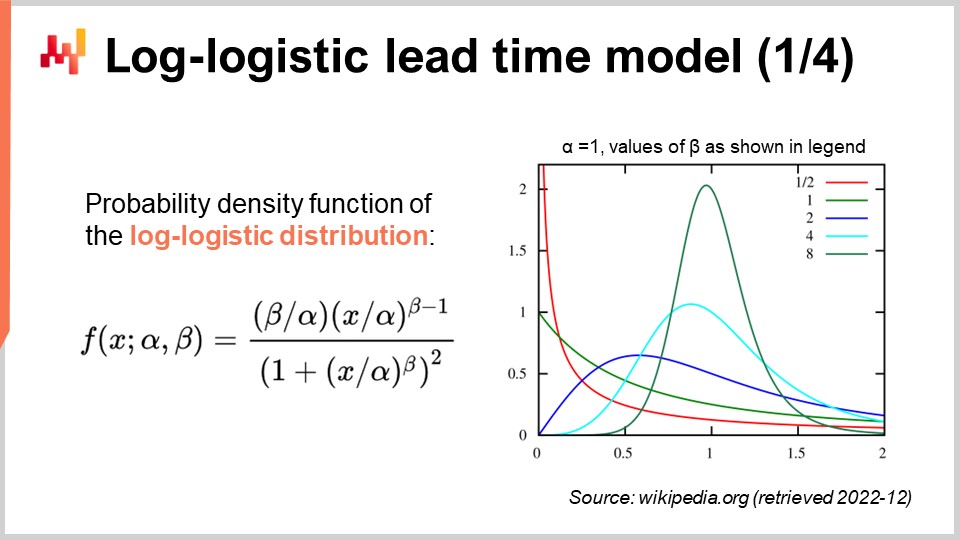
リードタイムはしばしば裾が重く、つまりリードタイムが逸脱すると、その逸脱は大きなものとなります。したがって、リードタイムをモデル化するには、裾重い挙動を再現できる分布を採用することが望ましいです。数学文献にはそのような分布が多数紹介されていますが、その全てを概観するだけでも数時間を要してしまいます。ここで強調したいのは、ポアソン分布には裾の重さがないという点です。そこで本日は、裾重い分布である対数ロジスティック分布を選びます。この分布を採用する主な理由は、Lokadのチームが複数のクライアントに対してリードタイムを対数ロジスティック分布でモデル化しており、最小限の複雑さでうまく機能しているからです。ただし、対数ロジスティック分布が万能の解決策であるわけではなく、Lokadが状況に応じてリードタイムを異なる方法でモデル化するケースも多く存在することを念頭に置いておくべきです.
画面には、対数・ロジスティック分布の確率密度関数が表示されています。これは2つのパラメータ、αとβに依存するパラメトリック分布です。αパラメータは分布の中央値を示し、βパラメータは分布の形状を制御します。右側には、さまざまなβ値によって得られる一連の形状が表示されています。この密度の式は一見威圧的に見えるかもしれませんが、球の体積を求める公式と同様に、教科書にある標準的な内容なのです。暗記しようとするかもしれませんが、実は解析的な式が存在することだけを知っていればよく、オンラインで再検索するのに1分もかかりません。

私たちの目的は、対数・ロジスティック分布を活用して確率的リードタイムモデルを学習することです。そのために、対数尤度を最小化します。実際、この第5章の前回の講義では、確率的視点に適したいくつかの指標を確認しました。少し前にCRPS(連続順位確率スコア)を再検討しましたが、今回はベイズ的視点を採用した対数尤度を再検討します。
要するに、2つのパラメータが与えられると、対数・ロジスティック分布は実際のデータセットで観測される各観測値が現れる確率を示します。私たちは、この尤度を最大化するパラメータを学習したいのです。対数、すなわち単なる尤度ではなく対数尤度を用いるのは、数値のアンダーフローを避けるためです。アンダーフローは、ゼロに非常に近い非常に小さな数値を扱う際に発生し、これらの数値は現代の計算機ハードウェアで一般的な浮動小数点表現と相性が悪いのです。
このように、対数・ロジスティック分布の対数尤度を計算するため、その確率密度関数に対して対数を適用します。その解析的表現が画面に示されています。この表現は実装可能であり、以下の3行のコードでまさにそのことが行われています。
1行目では「L4」関数が導入されます。L4は「log-logisticの対数尤度」を意味しており、たくさんのLと対数が登場します。この関数は、2つのパラメータαとβ、および観測値xの3つの引数を取ります。そして、この関数は尤度の対数を返します。関数L4はキーワード「autodiff」で装飾されており、これは自動微分によってこの関数が微分されることを意図していることを示します。つまり、この関数の戻り値からその引数であるαとβへ、勾配が逆伝播します。厳密には、観測値xを通しても勾配は伝わりますが、学習過程では観測値は不変とするため、勾配が観測値に影響を与えることはありません。3行目には、スクリプトの直上にある数学的式の逐語的な転写が示されています。
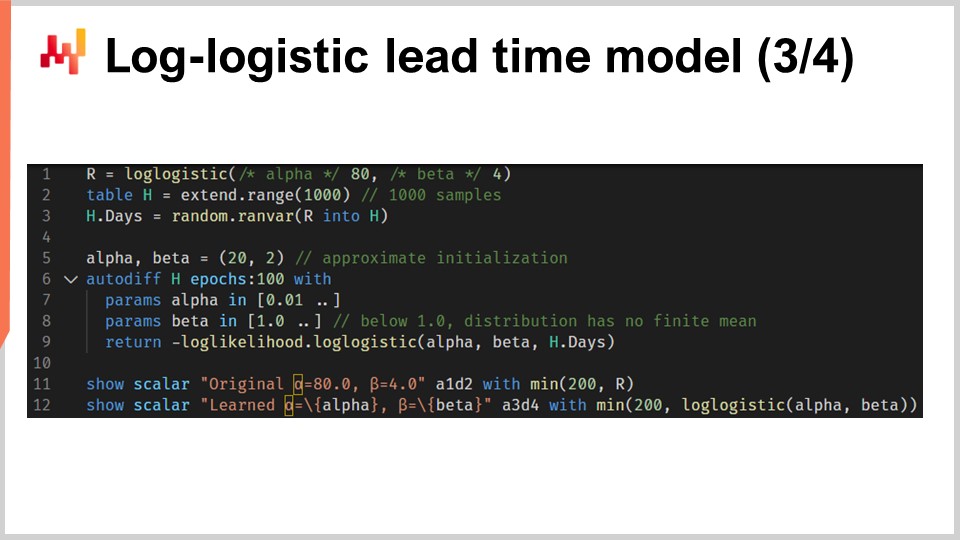
さて、対数・ロジスティック分布に基づく確率的リードタイムモデルのパラメータを学習するスクリプトを一緒に見ていきましょう。1行目と3行目では、モックのトレーニングデータセットを生成しています。実際の現場では、モックデータを生成するのではなく、過去のデータを使用するでしょう。1行目では、元の分布を表す「ranvar」を作成します。演習のため、これらのパラメータ、αとβを再学習したいのです。対数・ロジスティック関数はEnvisionの標準ライブラリの一部で、「ranvar」を返します。2行目では、1,000件のエントリを含むテーブル「H」を作成し、3行目では、元の分布「R」からランダムにサンプリングされた1,000個の偏差値を描画します。このベクトル「H.days」がトレーニングデータセットとなります。
6行目では「autodiff」ブロックがあり、ここで学習が行われます。7行目と8行目では、2つのパラメータ、αとβを宣言し、ゼロ除算などの数値問題を避けるためにこれらのパラメータに制約を設けています。αは0.01以上、βは1.0以上である必要があります。9行目では、対数尤度の逆数である損失を返します。実際、慣例として「autodiff」ブロックは損失関数を最小化するため、尤度を最大化するにはマイナス符号が必要となるのです。関数"log_likelihood.logistic"はEnvisionの標準ライブラリの一部ですが、その内部では、前のスライドで実装した関数L4を呼び出しているだけです。つまり、ここで特別な魔法が働いているわけではなく、すべて自動微分によって損失からパラメータαとβへ勾配が逆伝播しているのです。
11行目と12行目では、元の分布と学習された分布がプロットされます。ヒストグラムは200で上限が設定され、この上限によりヒストグラムが少し見やすくなっています。この点については後ほど詳しく説明します。また、このスクリプトの「autodiff」部分の性能について疑問に思われるかもしれませんが、単一のCPUコア上で実行して80ミリ秒未満で動作します。微分可能プログラミングは多才であるだけでなく、現代の計算機ハードウェアの計算資源を十分に活用しています。
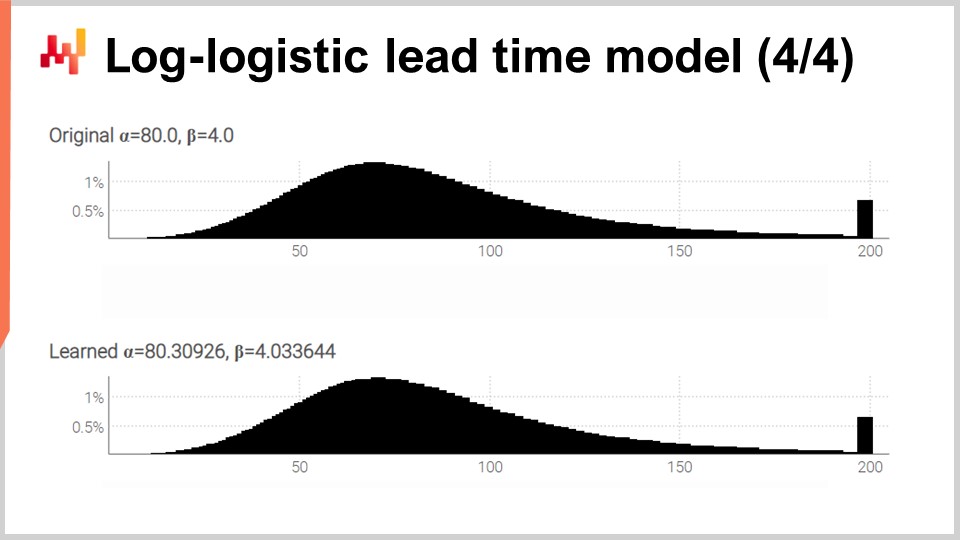
画面には、先ほどレビューしたスクリプトによって生成された2つのヒストグラムが表示されています。上部には、元の分布とその元のパラメータであるαとβ(それぞれ80と4)が示されています。下部には、微分可能プログラミングによって学習された2つのパラメータを持つ分布が示されています。右端にある2つのピークは、かなり伸びる尾部を切り捨てた結果に対応しています。ちなみに、稀ではありますが、注文されてから1年以上経過して商品が受領される場合もあります。これはすべての業界で当てはまるわけではなく、乳製品では特に見られませんが、機械部品や電子機器では時折見受けられます。
学習プロセスは完全ではないものの、元のパラメータ値から1%以内の結果が得られています。これは、少なくとも微分可能プログラミングによる対数尤度の最大化が実際に機能することを示しています。対数・ロジスティック分布が適切かどうかは、直面しているリードタイム分布の形状次第ですが、他の任意のパラメトリック分布を選択することも可能です。必要なのは、確率密度関数の解析的な表現だけです。こうした分布は数多く存在し、一度教科書にあるような式があれば、微分可能プログラミングでのシンプルな実装があとは自動的に行ってくれます。
リードタイムは、取引が完了した後に一度だけ観測されるものではありません。取引が進行中でも、何かしらの情報を得ており、不完全なリードタイムの観測値が存在します。例えば、100日前に注文を出したとしましょう。商品はまだ届いていませんが、リードタイムが少なくとも100日であることは既に把握できます。この100日の期間は、まだ完全には観測されていないリードタイムの下限を表しています。不完全なリードタイムはしばしば非常に重要なのです。講義の最初に述べたように、リードタイムのデータセットはしばしば希薄です。観測値がせいぜい6件しかないデータセットは珍しくありません。そのような場合、進行中の観測値も含め、すべての観測値を最大限に活用することが重要です。
次の例を考えてみましょう。注文は合計で5件あります。うち3件はすでに配達され、リードタイムは約30日でした。しかし、最後の2件は、それぞれ40日と50日間保留中です。最初の3件の観測からは、平均リードタイムは約30日であるべきですが、不完全な最後の2件がこの仮説を覆しています。40日と50日のバックオーダーは、リードタイムが実際にはかなり長いことを示唆しています。したがって、不完全だからといって最後の注文を捨てるべきではなく、この情報を活用して、リードタイムが60日程度になると信じを更新すべきなのです。
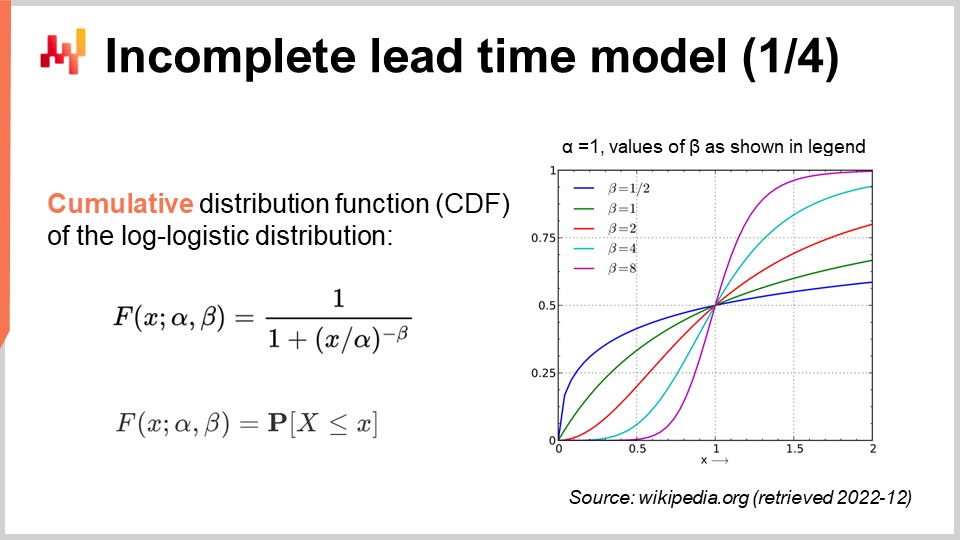
ここで、確率的リードタイムモデルを再検討し、今回は不完全な観測値も考慮に入れます。つまり、最終的なリードタイムの下限にすぎない観測に対処したいのです。そのために、対数・ロジスティック分布の累積分布関数(CDF)を使用できます。この式は画面に示されており、再び教科書にある内容です。対数・ロジスティック分布のCDFは、シンプルな解析表現という利点があります。以降、この技法を検閲データに対処する「条件付き確率技法」と呼びます。

このCDFの解析表現に基づき、対数・ロジスティック分布の対数尤度を再検討できます。画面上のスクリプトは、先ほどのL4実装の改訂版を提供しています。1行目では、ほぼ同じ関数宣言が行われています。この関数は第4の引数として、観測が不完全かどうかを示すBoolean値「is_incomplete」を追加で受け取ります。2行目と3行目では、もし観測値が完全であれば、従来の通常の対数・ロジスティック分布の場合と同様に、標準ライブラリの対数尤度関数を呼び出します。以前のL4実装のコードを繰り返すことも可能でしたが、今回のバージョンはより簡潔になっています。4行目と5行目では、現在の不完全な観測「X」より大きいリードタイムが最終的に観測される対数尤度を表現しています。これはCDF、正確にはその対数を通して実現されています。
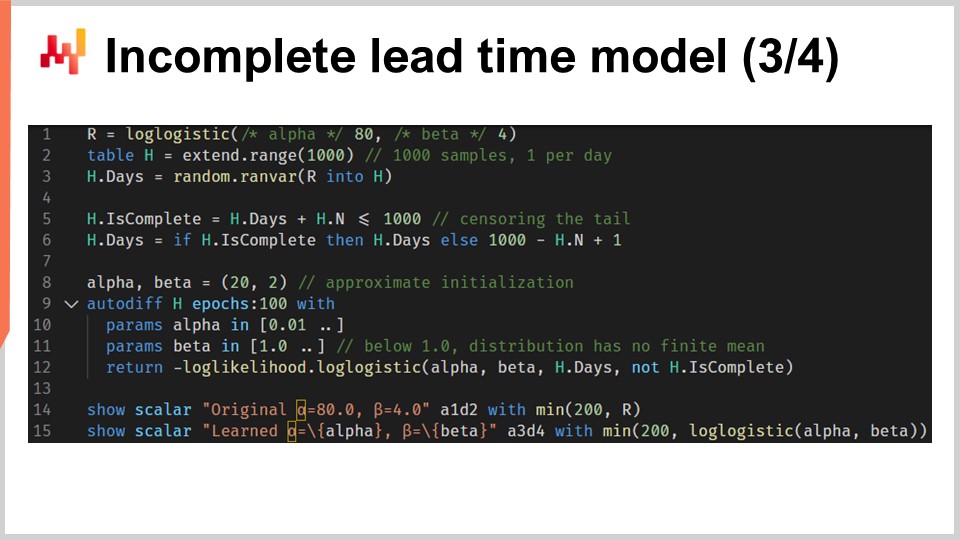
次に、不完全なリードタイムが存在する状況下で対数・ロジスティック分布のパラメータを学習するスクリプトを再現します。画面上のスクリプトは先ほどのものとほぼ同一です。1行目から3行目では、データを生成しており、これらの行は変更されていません。ここで、H.Nは2行目で暗黙的に生成される自動生成ベクトルで、生成された行に1から始まる番号を振っています。以前のバージョンではこの自動生成ベクトルは使われていなかったのですが、今回は6行目の末尾にH.Nベクトルが現れます。
5行目と6行目が特に重要です。ここではリードタイムを打ち切る(センサリング)処理を行っています。まるで、1日に1回のリードタイム観測を行い、あまりにも新しい観測値は情報が得られないために切り捨てているかのようです。例えば、7日前に開始された20日のリードタイムは、7日間の不完全なリードタイムとして現れます。6行目の終わりまでに、最近の観測値(現時点以降に終了するもの)が不完全なリードタイムのリストとして生成されます。残りのスクリプトは変更されておらず、唯一12行目でH.is_completeベクトルが対数尤度関数の第4引数として渡される点だけが異なります。つまり、12行目で先ほど導入した微分可能プログラミング関数を呼び出しているのです。
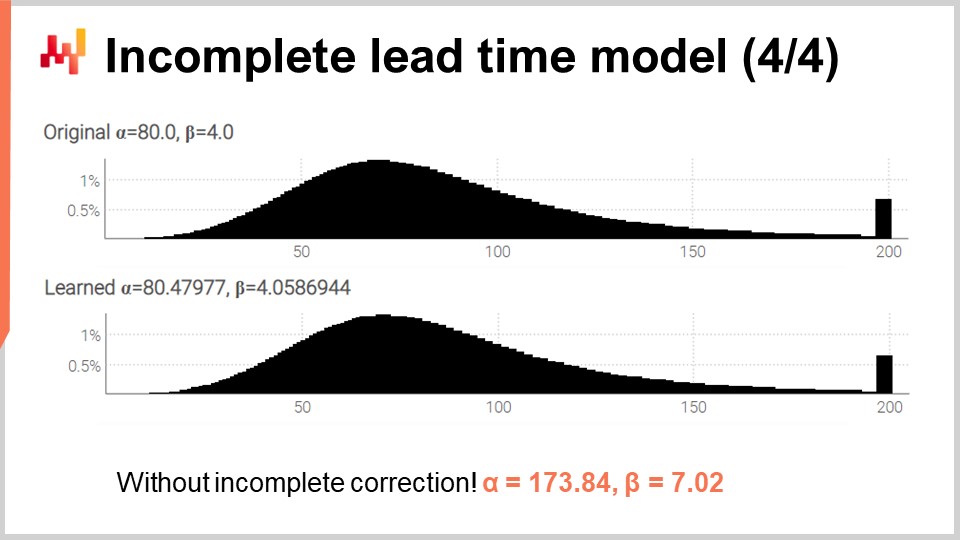
最後に、画面にはこの改訂版スクリプトによって生成された2つのヒストグラムが表示されます。多数の不完全なリードタイムが存在する中でも、パラメータは高精度で学習されています。不完全な観測値への対処が不必要な複雑さでなかったことを確認するため、スクリプトを再実行しましたが、今回は最初に全観測値が完全であると仮定した3引数の対数尤度関数の修正版を使用しました。αとβについては、画面下部に表示される値が得られ、予想通りそれらの値は元のαとβの値とは全く一致しませんでした。
この講義シリーズでは、検閲データに対処する技法が今回初めて紹介されるわけではありません。この章の第2講義では、ストックアウトに対処するために損失マスキング技法が紹介されました。実際、通常は将来の販売額ではなく将来の需要を予測したいのです。ストックアウトは、在庫切れがなければ発生したであろう全販売を観測できないため、下方のバイアスをもたらします。条件付き確率技法は、ストックアウトの場合と同様に検閲された需要に対処するために使用できます。条件付き確率技法は損失マスキングよりもやや複雑なため、損失マスキングで十分であれば、それ以上の手法は必要ないでしょう。
リードタイムの場合、データが希薄であることが主な動機となります。データが非常に少ない場合、不完全な観測値であっても、すべての観測値を最大限に活用することが極めて重要です。実際、条件付き確率技法は、不完全な観測値を単に捨てるのではなく活用する点で、損失マスキングよりも強力です。例えば、在庫単位が1つあり、その1つが販売された場合、ストックアウトを示唆するものとして、条件付き確率技法は需要が1以上であったという情報を活用します。
ここで、確率的モデリングの驚くべき利点が得られます。すなわち、多くのサプライチェーン状況で発生する検閲問題に対し、洗練された対処方法を提供してくれるのです。条件付き確率を活用することで、体系的なバイアスの多くのクラスを排除することが可能になります。
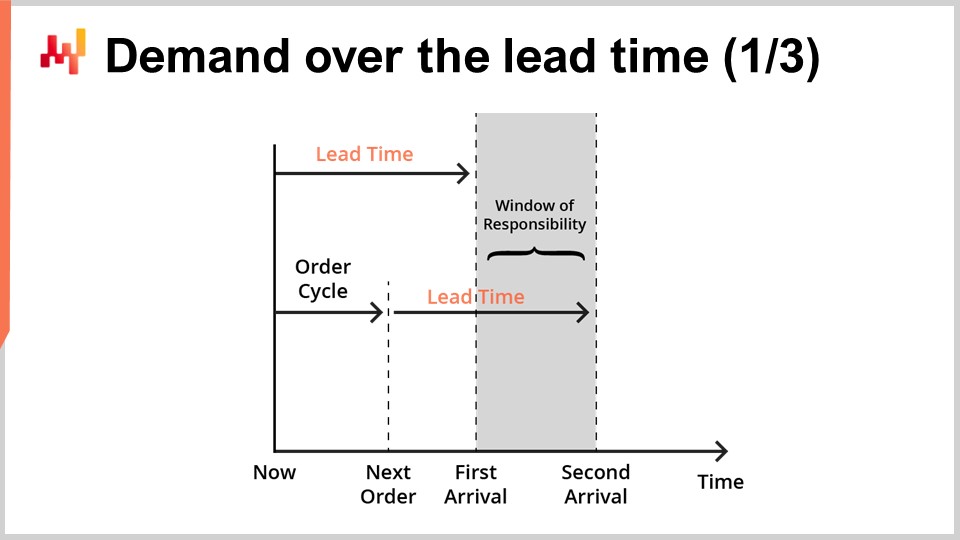
リードタイム予測は通常、需要予測と組み合わせて使用されることを意図しています。実際、画面に示されているような単純な在庫補充の状況を考えてみましょう。
私たちは単一の商品を扱っており、在庫は1社のサプライヤーから再注文することで補充されます。サプライヤーから再注文するかどうかの決定を支援する予測を求めています。今再注文すれば、商品は「第一到着」と記された時点に到着します。その後、再注文の機会が訪れ、「次回注文」と記された時点に再び注文可能となり、この場合、商品は「第二到着」と記された時点に到着します。「責任ウィンドウ」として示される期間が、再注文の判断において重要な期間となります。
実際、どんなに再注文を決定しても、最初のリードタイム前に届くことはありません。したがって、最初の到着前に発生する需要に対応する管理はすでに失われています。次に、後の再注文の機会が訪れるため、第二回目の到着後の需要に対応するのはもはや我々の責任ではなく、次の再注文の責任となります。従って、第二回目の到着後の需要に対応する意図で再注文を行うべきではなく、次の再注文の機会まで延期すべきです。
再注文の判断を支援するために、予測すべき要因は2つあります。まず、最初の到着時点での在庫残量の予測を行うべきです。実際、最初の到着時に十分な在庫が残っていれば、現時点で再注文する理由はありません。次に、責任期間内の需要の予測を行うべきです。現実の設定では、現在注文している商品の保管コストを評価するため、責任期間を越える需要も予測する必要があるかもしれません。しかし、簡潔さとタイミングのため、本日は責任期間内の在庫予測と需要予測に焦点を当てます。
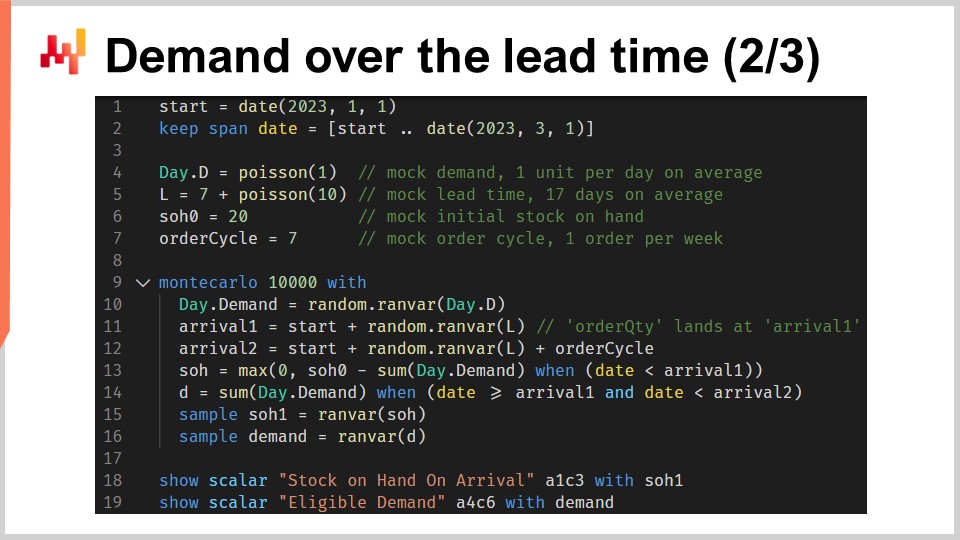
このスクリプトは、先ほど議論した責任期間の要因、すなわち予測を実装しています。入力として確率的リードタイム予測と確率的需要予測を受け取り、到着時の在庫量と責任期間内に発生する適格な需要という2種類の確率分布を返します。
1行目と2行目では、1月1日から始まり3月1日に終わるタイムラインを設定しています。予測の設定では、このタイムラインはハードコーディングされることはありません。4行目では、単純な確率的需要モデルが導入されます。これはタイムライン全体にわたって日ごとに繰り返されるポアソン分布であり、平均して1日あたり1単位の需要となります。明確さのために単純な需要モデルを使用していますが、実際の設定では、例えばESSM(エンセmbles状態空間モデル)を使用することも考えられます。状態空間モデルは確率的モデルであり、この章の最初の講義で紹介されました。
5行目では、もう一つの単純な確率的モデルが導入されます。この2番目のモデルはリードタイム用です。これは7日分右にシフトされたポアソン分布であり、そのシフトは畳み込みを通じて行われます。6行目で初期在庫を定義し、7行目で注文サイクルを定義します。この値は日数で表され、次回の再注文が行われるタイミングを示します。
9行目から16行目には、このスクリプトの核心となるモンテカルロブロックがあります。この講義の前半で、交差検証のロジックをサポートするために別のモンテカルロブロックを紹介しましたが、ここでは別の目的でこの構造を再利用しています。具体的には、到着時の在庫量と責任期間内の適格な需要という2つの確率変数をそれぞれ計算したいのです。しかし、確率変数の代数学だけではこの計算を十分に表現できないため、モンテカルロブロックが用いられています。
この章の第3回目の講義では、確率的予測とシミュレーションの間に二重性があることを指摘しました。モンテカルロブロックはこの二重性を示しています。まず確率的予測から始め、それをシミュレーションに変換し、最後にシミュレーションの結果を再び別の確率的予測に変換します。
細かい点を見てみましょう。10行目では、需要に対して1つの軌跡を生成します。11行目では、本日注文していると仮定して最初の注文の到着日を生成し、12行目では、今から1つの注文サイクル後に注文していると仮定して第二回目の注文の到着日を生成します。13行目では、最初の到着時の在庫残量を計算します。これは初期在庫から最初のリードタイム期間中に観測された需要を差し引いたものです。max zeroは在庫が負にならないことを意味しています。つまり、バックログは発生しないと仮定しています。このバックログなしの仮定は変更可能であり、バックログの場合は聴衆への演習として残されています。ヒントとして、微分可能なプログラミングを用い、在庫が再び利用可能になるまでの日数に応じて、未対応需要がどの程度バックログに変換されるかを評価することができます。
スクリプトに戻りますが、14行目では責任期間中に発生する需要、すなわち適格な需要を計算します。15行目と16行目では、“sample” キーワードを使って2つの重要な確率変数を収集します。この講義での最初のEnvisionスクリプト(交差検証を扱ったもの)とは異なり、ここでは単なる平均値ではなく、確率分布を収集しようとしています。15行目と16行目の両方で、代入の右側に現れる確率変数はアグリゲーターです。15行目では到着時の在庫量に関する確率変数を、16行目では責任期間内に発生する需要に関する別の確率変数を得ます。
18行目と19行目で、これら2つの確率変数が表示されます。さて、ここで一旦立ち止まり、このスクリプト全体を振り返ってみましょう。1行目から7行目はモックデータのセットアップでしかなく、18行目と19行目は結果の単なる表示に過ぎません。実際のロジックは9行目から16行目の8行の間に存在し、厳密には13行目と14行目にその核心が位置しています。
たった数行、厳密に数えて10行未満で、確率的リードタイム予測と確率的需要予測を組み合わせ、実際のサプライチェーンにおけるハイブリッドな確率予測を構築しています。ここで注目すべきは、リードタイム予測や需要予測の詳細に依存するものは一切なく、シンプルなモデルが用いられている点です。もっと洗練されたモデルを使用しても結果は変わらず、必要なのは2つの確率モデルがあれば、その軌跡を生成できるということです。
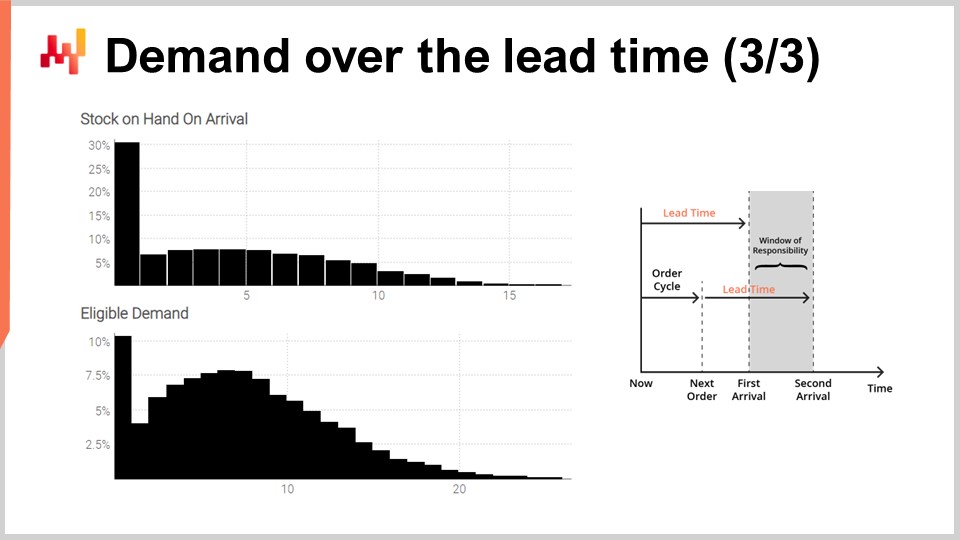
最後に、画面上にこのスクリプトによって生成されたヒストグラムが表示されます。上部のヒストグラムは到着時の在庫量を示しており、初期在庫がゼロとなる確率は概ね30%です。つまり、最初の到着日の直前に在庫切れが発生している可能性が30%あるということです。平均在庫量は約5単位かもしれませんが、この状況を平均値だけで判断すると、実情を大きく誤認することになります。初期在庫の状況を適切に反映するには、確率的予測が不可欠です。
下部のヒストグラムは、責任期間に関連する需要を示しています。需要がゼロとなる確率は概ね10%です。この結果は驚くべきものかもしれません。実際、今回の演習は平均して1日1単位の定常的なポアソン需要から始まりました。注文間隔は7日間であり、リードタイムが変動しなければ、7日間で需要がゼロとなる確率は0.1%未満であるはずです。しかし、スクリプトはこの事象がはるかに頻繁に発生することを示しています。その理由は、最初のリードタイムが通常より長く、第二のリードタイムが通常より短い場合に、責任期間自体が小さくなる可能性があるためです。
責任期間内に需要がゼロとなるということは、ある時点で在庫量が非常に高くなる可能性があることを意味します。状況によりこれは重大な問題となる場合もあればそうでない場合もありますが、たとえば保管容量に制限がある場合や、在庫が劣化性である場合には、致命的となる可能性があります。再び申し上げますが、平均需要(おそらく約8程度)だけでは需要の実情を信頼性をもって把握することはできません。平均1単位/日の定常需要から得られたこの非常に非対称な分布こそが、変動するリードタイム効果の現れなのです。
このシンプルなセットアップは、在庫補充の状況においてリードタイムがいかに重要であるかを示しています。サプライチェーンの観点から見ると、リードタイム予測と需要予測を分離するのは、せいぜい実用的な抽象化にすぎません。真に注目すべきは、日々の需要そのものではなく、需要とリードタイムの組み合わせなのです。もしバックログや返品などの他の確率的要因が存在すれば、それらもモデルの一部となっていたでしょう。

この講義シリーズの本章は、一般的なサプライチェーン教科書で通常「需要予測」と呼ばれるところを「予測モデリング」と題しています。この章のタイトルの意図は、本講義を進めるうちに次第に明らかになるはずです。実際、サプライチェーンの観点からは、サプライチェーンシステムの進化を予測することが求められます。需要は確かに重要な要因ですが、唯一の要因ではなく、リードタイムのような他の変動する要因も予測する必要があります。さらに何よりも大切なのは、これらすべての要因を最終的に統合して予測することです。
実際、これらの予測要素を統合して意思決定プロセスを支援する必要があります。したがって、重要なのは最終的な需要予測モデルを追求することではありません。この作業は、追加の精度が得られたとしても会社の最善の利益に反する形で行われるため、ほとんど無駄骨に終わる可能性が高いのです。モデルが洗練されればされるほど、不透明さ、バグ、計算資源の消費も増加します。経験則として、モデルが高度になればなるほど、別のモデルと運用上うまく連携させるのは困難になります。重要なのは、自由に組み合わせられる予測技術のコレクションを構築することです。これが予測モデリングにおけるモジュール性の本質です。本講義では、6種類程度の技術が紹介されました。これらの技術は、不完全な観測といった現実世界の重要な側面に対応するため有用であり、また非常にシンプルで、今日紹介したコード例のいずれも実際のロジックが10行を超えることはありませんでした。何よりも重要なのは、これらの技術がレゴブロックのようにモジュール化され、互いにうまく連携し、ほぼ無限に再構成可能であるという点です。
サプライチェーンにおける予測モデリングの究極の目的は、このような技術を特定することにあると理解されるべきです。各技術は、それ自体が既存の予測モデルを見直し、それを簡素化または改善するための機会となるべきです。

結論として、学術界でリードタイムがほとんど無視されているにもかかわらず、リードタイムは予測可能であり、予測されるべきです。現実のリードタイム分布の短いシリーズを検証することで、2つの課題が明らかになりました。まず、リードタイムは変動するということ、そして次に、リードタイムは断片的であるということです。したがって、断片的かつ不規則なリードタイムの観測に対処するための適切なモデリング技術を導入しました。
これらのリードタイムモデルは確率的であり、本章を通じて徐々に導入されてきたモデルの延長線上にあります。また、確率の視点が、在庫切れや保留中の注文などのサプライチェーンにほぼ遍在する不完全観測の問題に対して、優れた解決策を提供することも確認しました。最後に、後の意思決定プロセスを支援するために、確率的リードタイム予測と確率的需要予測を組み合わせ、必要な予測モデルを構築する方法を示しました。

次回の講義は3月8日、水曜日の午後3時(パリ時間)に行われます。本日の講義は技術的な内容でしたが、次回は主に非技術的な内容となり、サプライチェーン・サイエンティストの事例について議論します。実際、主流のサプライチェーン教科書は、予測モデルや最適化モデルが何の根拠もなく突如現れ機能するかのようにサプライチェーンを扱い、実際の「ウェットウェア」、つまり担当者の役割を完全に無視しています。したがって、定量的サプライチェーンイニシアティブを率いることが期待されるサプライチェーン・サイエンティストの役割と責任をより詳しく見ていきます。
それでは、質問に進みます。
質問: 万が一、ある人がさらなるイノベーションや、ジャストインタイム以外の理由で在庫を保持しておきたい場合はどうすればよいのでしょうか?
これは実に非常に重要な質問です。この概念は通常、サプライチェーンの経済モデル化、すなわち本講義シリーズで技術的に「経済ドライバー」と呼ばれるものを通じて扱われます。つまり、今日顧客に対応する代わりに、後の時点で同じ商品を何らかの理由でより重要な他の顧客、例えばVIP顧客に提供する機会があるため、敢えて今日の顧客にサービスを提供しない方が良いのかという問いです。本質的には、今日の顧客に対応するよりも、後で別の顧客に対応することでより大きな価値を獲得できるということを意味しています。
そのようなケースは実際に存在します。例えば航空業界において、あなたがMRO(メンテナンス、修理、オーバーホール)プロバイダーであるとしましょう。あなたには長期契約で定期的にサービスを提供している通常のVIP顧客、すなわち非常に重要な航空会社がいます。そうした場合、常にこれらの顧客に対応できるようにしたいものです。しかし、もし別の航空会社から1ユニットの問い合わせがあった場合、その顧客にサービスを提供することは可能ですが、彼らとは長期契約が結ばれていません。そこで、価格を非常に高く設定して、後の在庫切れの可能性を補うに足る価値を確保するのです。結論として、この最初の質問に対しては、これは単に予測の問題ではなく、むしろ経済ドライバーの適切なモデリングの問題だと考えます。在庫を保持したいのであれば、在庫を予備として保持している間に1ユニットを要求する顧客に対応しないという合理的な反応が得られる最適化モデルを構築することが求められます。
ところで、これもまた典型的な状況として、キットを販売している場合です。キットとは、多くの部品をまとめて販売するものであり、残った1つの部品は、キット全体の価値のほんの一部にしかならない場合があります。問題は、この最後の部品を売ってしまうと、キットを組み立て、その定価で販売することができなくなるという点です。したがって、後で(多少の不確実性はあるかもしれませんが)キットを販売できるように、在庫としてその部品を保持する方が望ましい状況に陥るかもしれません。しかし、結局は経済的要因に帰着するため、私ならこのように対処するでしょう。
質問: 近年、サプライチェーンの遅延は戦争やパンデミックが原因で多発しており、以前にはそのような状況がなかったため予測が非常に困難でした。これについてどのようにお考えですか?
私の見解では、リードタイムは昔から変動してきたということです。私は2008年からサプライチェーンの世界で働いており、両親は私より30年以上前からこの分野に携わっていました。記憶にある限り、リードタイムは常に不規則で変動してきました。抗議行動、戦争、関税の変更など、常に何かしらの事象が起こっています。確かに、過去数年は非常に不規則でしたが、もともとリードタイムはかなり変動していたのです。
誰も次の戦争やパンデミックを予測できると主張することはできません。もしそれらの出来事が数学的に予測可能であったなら、人々は戦争に加担したりサプライチェーンに投資したりするのではなく、株式市場で取引し、市場の動きを先読みして金持ちになっていたはずです。
要点は、予期せぬ事態に備えるということです。もし未来に自信が持てない場合、実際に予測のばらつきを大きく見積もることができます。これは、予測をより正確にするのとは逆で、平均的な期待はそのままに、テール部分を拡大し、その確率的予測に基づく決定が、変動に対してよりレジリエントになるようにするためです。つまり、現状よりも大きな予測上のばらつきを意図的に設計するのです。結局のところ、物事が予測しやすいか困難かという考えは、未来を正確に予測できるという前提に立ったポイント予測の視点から生まれるものであり、正確な未来予測というものは存在しません。唯一できるのは、未来に対する無知さを表現し定量化する、幅広い確率分布を用いることなのです。
正確な計画の微妙な実行に依存する決定を細かく調整する代わりに、ある程度の変動を見越して計画を立てることで、それらの変動に対する決定の堅牢性を高めることができます。しかし、これはサプライチェーンに過度な打撃を与えない範囲の変動にのみ当てはまります。例えば、より長いサプライヤーリードタイムには対処できても、もし倉庫が爆撃されれば、どんな予測もその状況を救うことはできません。
質問: Excelのadd-inである itsastat のような、様々な分布を提供するツールを使って、Microsoft Excelでこれらのヒストグラムを作成し、CRPSを計算することは可能でしょうか?
はい、可能です。Lokadのメンバーの一人が、在庫補充の状況を表す確率モデルをExcelのスプレッドシートで実装した実例があります。本質的な問題は、Excelにはネイティブのヒストグラムデータ型が存在しないため、Excelでは各セルに数値、すなわち1つの数字しか扱えない点にあります。もし1つのセルに完全なヒストグラムが格納できれば、非常にエレガントでシンプルなのですが、私の知る限り、Excelではそれは実現不可能です。しかしながら、もしヒストグラムを表現するために約100行ほどのコードを書く覚悟があるなら、コンパクトではなく実用性に欠けるものの、Excelで分布を実装し、確率的モデリングを行うことができます。例としてのリンクはコメント欄に掲載する予定です。
ここで注意すべきは、Excelがこの作業に最適ではないため、比較的骨の折れる作業になるということです。Excelは一種のプログラミング言語であり、何でも可能ですが、add-inなしで実現できる一方、非常に冗長なコードになるため、非常に整然としたものを期待しない方がよいでしょう。
質問: リードタイムは、注文時間、生産時間、輸送時間などの要素に分解されます。もしより細かくリードタイムを管理したい場合、このアプローチはどのように変わるのでしょうか?
まず、リードタイムの管理をより細かくするということは、平均リードタイムを短縮したいのか、あるいはリードタイムの変動性を低減したいのかという点を考慮する必要があります。興味深いことに、多くの企業が平均リードタイムの短縮に成功しましたが、その代償としてリードタイムのばらつきが増加するというトレードオフに直面しています。すなわち、平均的なリードタイムは短くなるが、時には大幅に長くなることもあるのです。
この講義では、モデリングの演習に取り組んでいます。それ自体は何ら行動を起こすわけではなく、観察、分析、および予測のためのものです。しかし、リードタイムを分解してその基礎となる分布を分析することで、どの要素が最も変動しているのか、またサプライチェーンに最も悪影響を与えているのはどの要素かを確率的モデルで評価することが可能になります。その情報を元に「もしこうだったら」といったシナリオを検討できます。例えば、リードタイムのある部分について「もしそのテールがもう少し短かったら、または平均がもう少し短かったらどうなるだろう?」と問い、すべてを再構成し、サプライチェーン全体の予測モデルを再実行して、その影響を評価することができます。
このアプローチにより、突発的な現象も含めた様々な現象について部分的に論理的に考えることが可能となります。これは新たなアプローチというより、これまで行ってきた手法の延長線上にあり、第6章ではこれらの確率的モデルに基づいた実際の意思決定の最適化について扱います。
質問: SAPでリードタイムを再計算し、より現実的な時間枠を提供することでシステムの引き込みや引き戻しを最小限に抑えることができると思いますが、可能でしょうか?
免責事項: SAPはサプライチェーン最適化分野におけるLokadの競合他社です。私の初期の回答としては、SAPではそれは実現不可能というのが実情です。実際、SAPにはサプライチェーン最適化を扱う4種類の異なるソリューションが存在し、どのスタックの話をしているかに依存します。しかし、これらすべてのスタックに共通しているのは、ポイント予測に重点を置いたビジョンであるという点です。SAPのすべては、予測が正確であるという前提の下に設計されています。
はい、SAPには最初に述べた正規分布のように調整可能なパラメータがいくつかあります。しかし、私が観察したリードタイムの分布は正規分布ではありません。私の知る限り、主流のSAPのサプライチェーン最適化設定はリードタイムに正規分布を仮定しています。問題は、ソフトウェアの根幹で大きく誤った数学的仮定がなされている点にあります。ソフトウェアアーキテクチャの核心に入り込む広範囲な誤った仮定から、単にパラメータ調整で回復することはできません。理論上は、逆算して正しい決定を生み出すパラメータを見つけ出すことは可能かもしれませんが、実際には数多くの問題が発生するため、本当にその価値があるのか疑問です。
確率的視点を採用するには、予測自体が確率的であり、最適化モデルも確率モデルを利用する必要があります。問題は、たとえリードタイムの予測がわずかに改善されたとしても、SAPのその他の部分は結局ポイント予測に戻ってしまうという点です。どんなに工夫しても、結局はそれらの分布は一点に圧縮されてしまうのです。平均値で近似できるという考えは、憂慮すべきことだけでなく、根本的に誤りです。したがって、技術的にはリードタイムを調整することは可能ですが、その後に発生する多くの問題を考えると、実施する価値があるかは疑問です。
質問: 同じ部品を複数の供給業者から注文する状況があります。これは、リードタイム予測において重要な情報ですが、アイテムごとにリードタイム予測を行うべきでしょうか、それともアイテム群をまとめる方法を取る場合があるのでしょうか?
これは非常に興味深い質問です。もし同じ品目に対して2社の供給業者がいる場合、問題は品目と供給業者の類似性の程度に依存します。まず状況を見極める必要があります。一方の供給業者が隣接しており、もう一方が地球の反対側にあるならば、これらは別々に扱うべきです。しかし、ここでは2社の供給業者がかなり似通っており、同じ品目を扱っているという興味深い状況を仮定します。その場合、これらの観測値をまとめるべきかどうかが問題となります。
興味深いのは、微分可能なプログラミングを活用することで、供給業者に対する重みと品目に対する重みを組み合わせ、学習の力にその役割を任せるモデルを構築できる点です。これにより、リードタイムの中で品目の要素により多くの重みを置くべきか、供給業者の要素に重みを置くべきかが自動的に調整されます。どちらか一方の供給業者が平均して若干早いというバイアスが存在する可能性もありますが、品目によっては処理に時間がかかるものもあり、どちらが速いかはどの品目を見ているかによって大きく異なってしまいます。すべてを供給業者と品目ごとに細分化してしまうと、十分なデータが得られなくなるでしょう。したがって、ここでお勧めするのは、微分可能なプログラミングを活用して、部品レベルのパラメーターと供給業者レベルのパラメーターの両方を導入する方法です。そうすれば、パラメーターの総数が部品数×供給業者数になるのではなく、部品数と供給業者数の合計、あるいは供給業者のカテゴリー数を加えた程度に抑えられ、パラメーター数が爆発することなく、供給業者に関連する要素を追加して、過去のデータに基づいた動的なミックスを実現できるのです。
質問: 注文数および一緒に注文される製品も最終的にリードタイムに影響を与えると思います。この種の問題に全ての変数を含める複雑性について詳しく説明していただけますか?
前述の例では、2種類の期間がありました。ひとつは注文サイクル、もうひとつはリードタイムそのものです。注文サイクルは、まだ決定されていないために不確実性が生じる点で興味深いです。これは基本的に、ほぼいつでも決定可能なものであり、完全に自分たちの手で決定できる内部要因です。これはサプライチェーンにおいて価格など、他の要素も同様です。需要は存在し、観測されますが、実際に設定する価格も自分たちで決めるものです。明らかに不適切な価格設定もありますが、それは全て自分たちで決定しているのです。
注文サイクルは自分たちで決定するものです。さて、あなたがおっしゃるのは、次の注文のリードタイムが正確なタイミングで発生するかどうかの不確実性、つまりいつ注文が行われるかが不明であるという点です。確かにその通りです。確率的モデリングを実装できると、第六章で議論するように、注文サイクルを単に「7日」と定義するのではなく、企業の投資収益率を最大化する再注文ポリシーを採用すべきになるのです。つまり、今日の最適な注文判断は、まだ下されていない次の注文判断に依存する―いわば「蛇が自らの尾を噛む」状況になってしまうのです。この種の問題はポリシー問題、すなわち連続的な意思決定問題として知られています。根本的には、意思決定プロセスを規定する数学的な対象、すなわちポリシーを構築することが求められるのです。
ポリシー最適化の問題は非常に複雑であり、これについては第六章で詳しく扱う予定です。しかし、要点としては、あなたの質問に戻ると、2つの異なる要素が存在するということです。一つは、あなたが何もしなくても独立して変動する供給業者リードタイムという要素、そしてもう一つは、内部プロセスに依存して最適化されるべき注文タイミングという要素です。
これにより、最終的には最適化と予測モデルが収束することが分かります。結局、どちらも相互に影響し合っており、ほぼ同じものになってしまうのです。
本日はこれで以上です。お忘れなく、3月8日、同じ時間にお会いしましょう。水曜日の午後3時です。ありがとうございました。それでは、また次回お会いしましょう.


