00:00 Introduction
02:53 Decisions vs Artifacts
10:07 Experimental optimization
13:51 The story so far
17:01 Today’s decisions
19:36 The manifesto of the quantitative supply chain
21:01 The retail stock allocation problem
24:49 Economic forces on the store SKU
29:35 Reifying the futures
32:41 Reifying the options - 1/3
38:25 Reifying the options - 2/3
43:02 Reifying the options - 3/3
44:44 Stock reward function - 1/2
51:41 Stock reward function - 2/2
56:19 Prioritized stock allocations - 1/4
59:59 Prioritized stock allocations - 2/4
01:03:39 Prioritized stock allocations - 3/4
01:06:34 Prioritized stock allocations - 4/4
01:12:58 Smoothing the warehouse flow - 1/2
01:16:48 Smoothing the warehouse flow - 2/2
01:22:12 Action reward function
01:25:02 The real world is messy
01:27:38 Conclusion
01:30:00 Upcoming lecture and audience questions
説明
サプライチェーンの意思決定にはリスク調整済みの経済評価が必要です。 確率的予測を経済評価に変換することは容易ではなく、専用のツールが求められます。しかし、在庫管理で示されるような結果としての経済的な優先順位付けは、伝統的な手法よりもはるかに強力であることが証明されています。私たちは小売在庫配分の課題から始めます。流通センター(DC)と複数の店舗を含む2層ネットワークにおいて、すべての店舗が同じ在庫を巡って競合していることを踏まえ、DCの在庫をどの店舗に配分するかを決定する必要があります。
完全文書き起こし

このサプライチェーン講義シリーズへようこそ。私はジョアンネス・ヴェルモレルです。今日は「確率的予測を用いた小売在庫配分」についてご説明します。小売における在庫配分はシンプルでありながら根本的な課題です。すなわち、運営する流通センターと店舗間で、いつ、どれだけの在庫を移動させるかという問題です。在庫移動の決定は将来の需要に依存するため、何らかの需要予測が必要となります。
しかしながら、店舗レベルでの小売需要は不確実であり、未来の需要の不確実性は根本的に排除できません。この根本的な不確実性を適切に反映する予測が必要であるため、確率的予測が求められます。それにもかかわらず、サプライチェーンの最適化意思決定のために確率的予測を最大限に活用することは容易ではありません。従来の決定論的予測を前提に設計された既存の在庫手法を転用したくなるかもしれませんが、そうすると確率的予測を導入した根本的な理由が失われてしまいます。
この講義の目的は、サプライチェーンの意思決定を最適化するために、確率的予測をそのままの形で最大限に活用する方法を学ぶことにあります。最初の例として、小売在庫配分の問題を検討し、この問題を通じて店舗レベルでの在庫水準を実際に最適化する方法を見ていきます。さらに、確率的予測の検証により、流通センターから店舗への在庫フローを平滑化し、ネットワークの運用コストを最適化・削減するといった新たなクラスのサプライチェーン問題にも取り組むことが可能になります。
この講義は、サプライチェーンにおける意思決定の技法とプロセスに捧げられたシリーズの第6章の始まりです。ここでは、意思決定は個々の局所的な最適化を行うのではなく、サプライチェーン全体を統合したシステムとして考慮して最適化されるべきであることを確認します。例えば、SKU(在庫管理単位)を狭い視点でのみ捉えることの問題などが挙げられます。
サプライチェーンの意思決定に取り組む最初のステップは、実際のサプライチェーン意思決定を明確にすることです。サプライチェーンの意思決定は、サプライチェーンに直接的かつ物理的な影響を与えます。例えば、流通センターから店舗へ在庫を1単位移動させる行動は現実のものであり、その瞬間、店舗の棚に1単位が加わり、流通センターからは1単位が欠落し、他の場所へ再配分することはできなくなります。
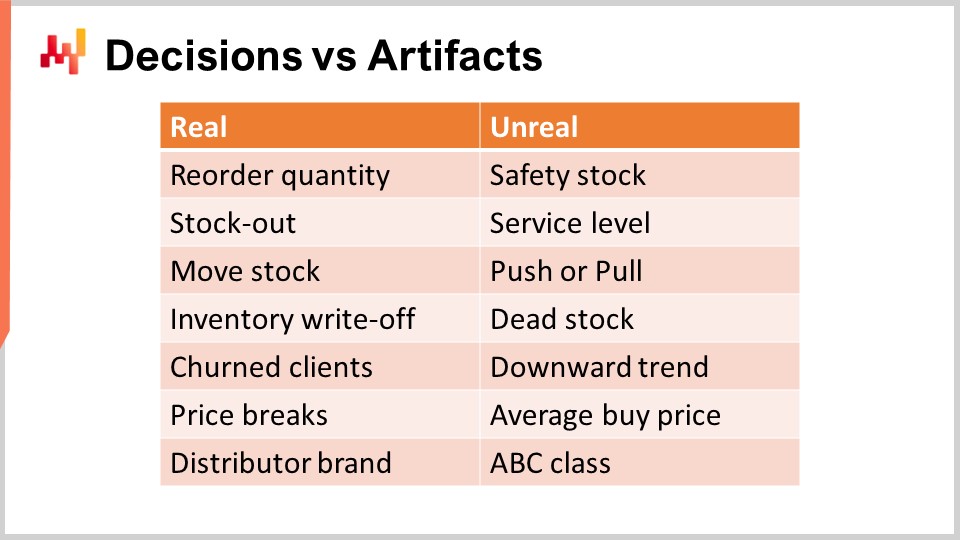
対照的に、アーティファクトはサプライチェーンに直接的な物理的影響を与えません。アーティファクトとは、通常、サプライチェーンの意思決定に至る中間的な計算工程であるか、もしくはサプライチェーンシステムの一部の特性を表す統計的な推定値のことです。残念ながら、サプライチェーンに関する文献では、意思決定とアーティファクトの区別について多くの混乱が見受けられます。
注意すべきは、投資収益は意思決定の改善によってのみ得られるということです。アーティファクトの改善はほとんど意味をなしません。場合によっては、企業がアーティファクトの改善に過度に時間を費やすと、それが実際のサプライチェーン意思決定の改善を妨げる気晴らしになってしまいます。画面には、主流のサプライチェーン関係者の間でしばしば見受けられる混乱のリストが示されています.
例えば、安全在庫について考えてみましょう。この在庫は実在するものではなく、安全在庫と実働在庫の2種類が存在するわけではありません。在庫は1種類のみで、唯一の判断は追加が必要かどうかという点です。再発注する数量は現実的なものですが、安全在庫自体はそうではありません。同様に、サービスレベルも実在するものではありません。サービスレベルは非常にモデル依存的であり、実際の小売需要では販売データが乏しいため、任意のSKUに対して十分なデータがなく、有意なサービスレベルを算出するのは困難です。サービスレベルにアプローチする方法はモデリング技法や統計的推定を用いることであり、これは問題ありませんが、これもまたアーティファクトであって現実そのものではありません。これは、サプライチェーンに対して持つ数学的視点の一例にすぎません.
同様に、プッシュかプルかという問題も視点の問題です。サプライチェーン全体のネットワークを考慮に入れた適切な数値的レシピは、ある起点から目的地へ在庫を1単位移動させる可能性のみを考慮します。現実なのは在庫の移動そのものであり、その在庫移動を起点の条件に基づいて発動するか、あるいは目的地の条件に基づいて発動するかは単なる視点の問題です。これがプッシュかプルかを定義しますが、多くても数値的レシピの些細な技術的詳細に過ぎず、サプライチェーンの核心的現実を示すものではありません.
デッドストックとは、近い将来に在庫の償却リスクがある在庫の推定値に過ぎません。クライアントの視点からは、デッドストックと生在庫という区別はなく、どちらも魅力が異なる製品であっても、本質的には在庫に対するある種のリスク評価です。これは問題ありませんが、最終的な在庫償却、すなわち価値が失われたことを示すものと混同してはなりません.
同様に、下降傾向も観察される需要をモデル化する際に存在しうる数学的要素のひとつです。通常、需要モデルにおいては時間依存の要因、例えば時間に対する線形依存や指数関数的依存が導入されます。しかし、これ自体が現実を正確に反映しているわけではありません。現実には、顧客の喪失などによりビジネスが低下している可能性があり、離脱率などがサプライチェーンの実態を示しています。下降傾向は単にパターンを集約するために用いられるアーティファクトにすぎません.
同様に、いかなるサプライヤーも平均購入価格で製品を販売することはありません。現実は、購入注文書を作成し、数量を選定し、その数量に応じてサプライヤーが提供する価格優遇を活用できるということです。その結果、価格優遇や交渉によって決まる購入価格が適用されます。平均購入価格は実在するものではないため、これらの数値的アーティファクトを根本的な真実と捉えないよう注意してください.
最後に、トップセラーから回転の遅い製品までを分類するABC分析は、単なる取り扱い量に基づくSKUや製品の些細な分類に過ぎません。これらのクラスは実際の属性ではありません。通常、製品の半数は四半期ごとにABCクラスが変動しますが、クライアントや市場の視点からはそれほど大きな変化はありません。これは単なる数値的アーティファクトであり、例えば製品がディストリビューターブランドに属しているかどうかといった、サプライチェーンに大きな影響を与える根本的な属性と混同すべきではありません。本章では、数値的アーティファクトに時間や労力を浪費するのではなく、サプライチェーンの意思決定に注力することの重要性が次第に明らかになるでしょう.
「最適化」という言葉が聞かれると、知識豊富な聴衆には通常、数学的最適化の視点が思い浮かびます。ある一群の変数と損失関数が与えられた場合、その目標は損失関数を最小化する変数の値を見つけ出すことにあります。しかし、このアプローチは、関連する変数が既知であることを前提としているため、サプライチェーンではうまく機能しません。たとえ変数が既知であっても、天候データのようにサプライチェーンに大きな影響を与える多数の変数が存在し、そのデータ取得には莫大なコストが伴うため、データ取得の労力に見合うかは明らかではありません.
さらに厄介なのは、損失関数自体がほとんど未知である点です。損失関数は何とか推定することは可能ですが、サプライチェーンから得られる実世界のフィードバックと損失関数との対峙によってのみ、この損失関数の適切性に関する有効な情報が得られます。これは数学的な正しさの問題ではなく、適合性の問題です。この数学的構成物である損失関数が、サプライチェーンの最適化対象を十分に反映しているかどうかは疑問です。この「変数と損失関数が未知である中での最適化」という難問に、講義2.2「実験的最適化」で取り組みました。実験的最適化の視点では、問題は既に与えられているのではなく、繰り返しの実験を通して発見されなければならないと説いています。損失関数とその変数の正しさの証明は、数学的性質として現れるのではなく、サプライチェーン自体から得られた適切な実験に基づく一連の観察を通して明らかになるのです。実験的最適化は最適化に対する我々の見方に根本的な挑戦を突きつけるものであり、本章で採用する視点でもあります。ここで紹介するツールと技法は、実験的最適化の視点に基づいています.
どの時点においても、現在用いている数値的レシピは陳腐化していると宣言され、我々のサプライチェーンにより適合すると判断される別の数値的レシピに置き換えられる可能性があります。したがって、新たな数値的レシピが生まれるたびに、それを直ちに生産環境に投入し、サプライチェーンの意思決定にその恩恵がすぐに反映されるよう、大規模な最適化プロセスを実行できる状態にしておく必要があります。例えば、損失関数を特定した後、3ヶ月間データサイエンティストのチームを投入してソフトウェア最適化技法を構築する、ということはできません.
この講義はサプライチェーン講義シリーズの一部です。これらの講義はある程度独立して視聴可能なようにしていますが、提示された順序で視聴したほうが理解しやすい段階に来ています。以前の講義をまだ視聴していなくても問題はありませんが、このシリーズは提示された順序で視聴するのが最も理解しやすいでしょう.
第1章では、サプライチェーンを学問分野として、また実践としての見解を示しました。第2章では、実験的最適化を含むサプライチェーンの課題に対処するための一連の手法を提示しました。これらの手法は、ほとんどのサプライチェーン問題が対立的な性質を持つために必要とされます。第3章では、解決策ではなく問題そのものに焦点を当てました。第4章では、厳密にはサプライチェーンそのものではなく、サプライチェーンの補助となる学問分野を紹介し、現代のサプライチェーン実践に不可欠であることを示しました。第5章では、将来の排除できない不確実性に対処するために不可欠な、特に確率的予測をはじめとする一連の予測モデリング技法を提示しました.
今日、この第6章の最初の講義では、意思決定手法に踏み込みます。科学文献では、1950年代の動的計画法から強化学習、さらには深層強化学習に至るまで、過去70年間にわたって無数の意思決定手法とアルゴリズムが発表されてきました。しかし、問題は生産グレードのサプライチェーン成果を実現することにあります。実際、これらの手法のほとんどは、何らかの理由でサプライチェーンの目的には実用的でない隠れた欠陥を抱えています。今日は、小売在庫配分というサプライチェーン意思決定の典型例に焦点を当てます。この講義は、より複雑な意思決定や状況への道を切り開くものです。
画面には本日の講義の概要が示されています。最も単純なサプライチェーン問題である小売在庫配分でさえ、取り扱う範囲は意外と広いのです。これらの要素は、より複雑な状況のための構成要素を表しています。まず、定量的サプライチェーンのマニフェストを再確認し、その後、小売在庫配分問題の意味を明確にします。また、この問題に存在する経済的要因についても見直します。さらに、確率的予測という概念と、それを実際に(もしくはその一つの表現方法として)どのように表現するかについても再検討します。予測と候補となる意思決定(選択肢)の精緻化によって、どのように意思決定をモデル化するかを見ていきます。
次に、在庫報酬関数を導入します。この関数は、一連の経済的要因を考慮に入れ、確率的予測を各在庫配分選択肢に関連づける経済的スコアへと変換するための最小限のフレームワークと見なすことができます。選択肢にスコアが付与されると、優先順位リストを作成することができます。この優先順位リストは一見単純に見えますが、数値的安定性とホワイトボックス化の面で、現実のサプライチェーンにおいて非常に強力かつ実用的なものとなります。
この優先順位リストを活用することで、配送センターから店舗への在庫フローをほぼ手間なく平滑化し、配送センターの運用コストを低減することができます。最後に、アクション報酬関数について簡単に概観します。今日、この関数はシンプルさを除けば、ほぼあらゆる面でLokadにおける在庫報酬関数に取って代わっています。
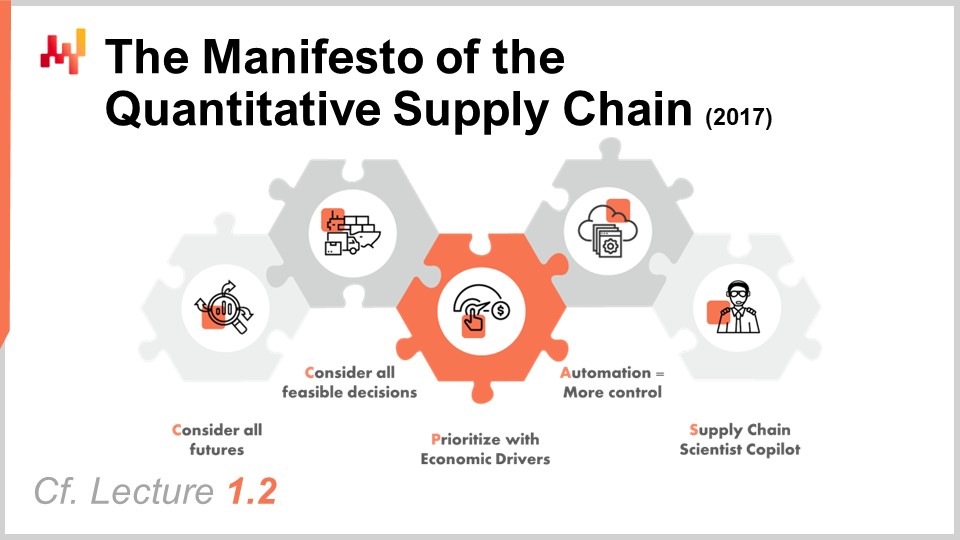
定量的サプライチェーンのマニフェストは、私が2017年に初めて発表した文書です。この視点は講義1.2で広く取り上げられましたが、明瞭さのために本日は簡単におさらいします。柱は5つありますが、今回我々に関連するのは最初の3つだけです。最初の3つの柱は以下のとおりです:
あらゆる可能な未来を考慮すること、つまり確率的予測だけでなく、変動するリードタイムや将来の価格など、不確実性を伴うその他すべての要素を予測することです。 実行可能なすべての意思決定を考慮し、成果物ではなく意思決定そのものに注目することです。 経済的ドライバーに基づいて優先順位をつけること、これが本日の講義の主題です。
特に、確率的予測をどのようにして経済的リターンの見積もりに変換できるかを見ていきます。
小売在庫配分問題において。これは私が定義するものですが、やや恣意的ではありますが、本日の講義ではこの定義を用います。私たちは、配送センターと複数の店舗という2層のネットワークを仮定します。配送センターはすべての店舗にサービスを提供しており、もし複数の配送センターが存在する場合でも、各店舗は単一の配送センターからのみサービスを受けると仮定します。目的は、配送センターに存在する在庫を適切に各店舗に配分することであり、すべての店舗が同一の在庫を巡って競合するのです。
すべての店舗は、配送センターからの毎日のスケジュールに沿って日々補充されると仮定します。したがって、毎日、各店舗ごとに各製品の何ユニットを移動させるかを決定しなければなりません。移動させる総ユニット数は、配送センターにある在庫を超えることはできず、また店舗の棚容量にも制限があることが合理的に考えられます。仮に配送センターの在庫が無限であれば、在庫をどの店舗に配分するかでアービトラージやトレードオフをする必要がなくなり、問題は単一段階のサプライチェーンとなってしまいます。ネットワークの二層性は、店舗が同じ在庫を巡って競合するという事実からのみ生じるのです。
当然、店舗の売上や、配送センターおよび店舗レベルでの在庫状況が把握できると仮定します。つまり、取引データが利用可能であるということです。また、配送センターで行われる入荷については、不確実性を伴う到着予定時刻(ETA)とともに既知であると仮定します。さらに、製品の仕入れ価格、販売価格、場合によっては製品カテゴリなど、地味ながらも重要な情報がすべて利用可能であると仮定します。これらの情報は、たとえ30年前のものであっても、あらゆるERPやWMS、およびPOSシステムに含まれているはずです。
本日は、配送センター(DC)の補充をこの問題に含めていません。実際、配送センターの補充と店舗への配分は密接に関連しているため、通常はこれらの問題を同時に扱います。しかし、明瞭かつ簡潔に講義を進めるため、本日はより単純な問題から取り組むことにしています。ただし、本日提示するアプローチは、自然に配送センターの補充も含められるように拡張可能であることに留意してください。

特定の日に特定の製品について、店舗へ在庫を1ユニット追加で移動させるかどうかは、一連の経済的要因に依存します。もしその移動が利益を生むのであれば、実施したい、そうでなければ実施しません。画面に主要な経済的要因が示されており、本質的に、店舗に在庫を多く置くことは一連の利益をもたらします。これには、販売機会損失を回避することによる粗利益の増加、品切れの減少によるサービス品質の向上、そして店舗の魅力度の向上が含まれます。実際、店舗が魅力的であるためには、豊富に在庫しているように見える必要があります。そうでなければ、店舗は寂しげに見え、消費者が購入に消極的になる可能性があります。これは小売における一般的な観察事項ですが、必ずしもハードラグジュアリーなどすべてのセグメントに当てはまるわけではありません。しかし、一般商品やファッション店舗においては、この考えは有効です。
残念ながら、在庫を増やすことには欠点もあり、店舗に多く在庫があることで期待できるリターンが逓減してしまいます。これらの欠点には、追加の保管コスト(在庫過剰の場合、在庫評価損につながることもあります)や、店舗スタッフが大量の出荷を処理できず、受入過負荷が生じるリスクなどが含まれます。もし納入量がスタッフの棚への陳列能力を超えると、店舗内で混乱と無秩序が生じます。さらに、機会費用という側面もあり、ある店舗に1ユニット配置すれば、別の店舗に配置することはできなくなります。配送センターに返送して再配分することは可能ですが、通常非常に高コストであるため、最後の手段となります。小売業者は、在庫を戻す必要のない効率的な店舗配分を目指すべきです。
また、在庫の流れをスムーズにすることも非常に望ましいです。配送センター(DC)は、経済的効率がピークに達する名目上の容量を持っています。このピーク効率は、DCの物理的な配置や、そこに配置された常勤スタッフの数に左右されます。理想的には、DCは日々運用され、その名目上の容量に非常に近い状態で稼働することで、最もコスト効率が良くなります。しかし、配送センターでピーク効率を維持するには、DCから各店舗への流れを平滑化する必要があります。経済的観点は、伝統的なサービスレベル志向の観点とは異なり、我々はパーセンテージではなく、ドル単位のリターンを求めています。ネットワークレベルで在庫配分スキームを調整し、運用コストを削減することと、店舗でのサービス品質がわずかに低下することのトレードオフが妥当かどうかを判断する唯一の方法は、ここで提示する経済的視点を採用することにあります。サービスレベルの視点では、このような判断は下せません。我々の現時点での目標は、与えられた在庫配分の意思決定に対して経済的成果を見積もる数値的レシピを確立することです。
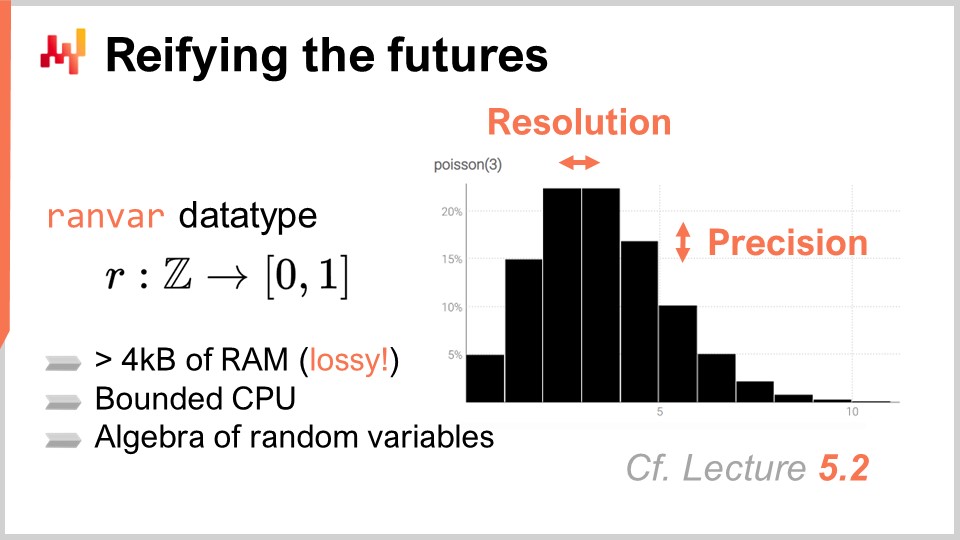
前章、第5章では、確率的予測の作成方法について議論し、一次元離散確率分布を表す特殊なデータ型「ranvar」を紹介しました。要するに、ranvarはEnvisionにおける単純な一次元確率的予測を表現するための特殊なデータ型です。
Envisionは、サプライチェーンの予測最適化を目的としてLokadによって設計されたドメイン固有のプログラミング言語です。これらの講義においてEnvision自体に本質的な独自性はありませんが、プレゼンテーションの明瞭さと簡潔さのために使用されています。本日説明する数値レシピは、Python、Julia、Visual Basicなど、どの言語でも実装可能です。
ranvarの重要な側面は、高性能な確率変数の代数演算を提供する点にあります。パフォーマンスは、計算コスト、メモリコスト、そして許容できる数値近似の度合いとのバランスです。小売ネットワークを扱う際、SKUは数百万、あるいは数千万に達する可能性があり、それぞれが少なくとも一つの確率的予測またはranvarを持つため、計算性能が極めて重要です。その結果、数百万から数千万のヒストグラムが生成されることもあり得ます。
ranvarの、ヒストグラムと比較した際の主な特性は、CPUコストとメモリコストの両方を上限付きで可能な限り低く抑える点にあります。また、導入される数値近似がサプライチェーンの観点から無視できるものであることを保証することも極めて重要です。ここで扱っているのは科学計算ではなくサプライチェーン計算であることに留意してください。数値計算は正確であるべきですが、極端な精度は必要ありません。つまり、十億分の一程度の近似誤差があっても、サプライチェーンの観点からは影響は無視できるのです。数値計算は正確さを求められますが、過度な精度は求められません。
以下では、確率的予測は特定のデータ型を持つ変数の集まりであるranvarsとして提供されると仮定します。実際には、ranvarsをヒストグラムに置き換えても、パフォーマンスや利便性の面を除けば、ほぼ同様の成果が得られます。
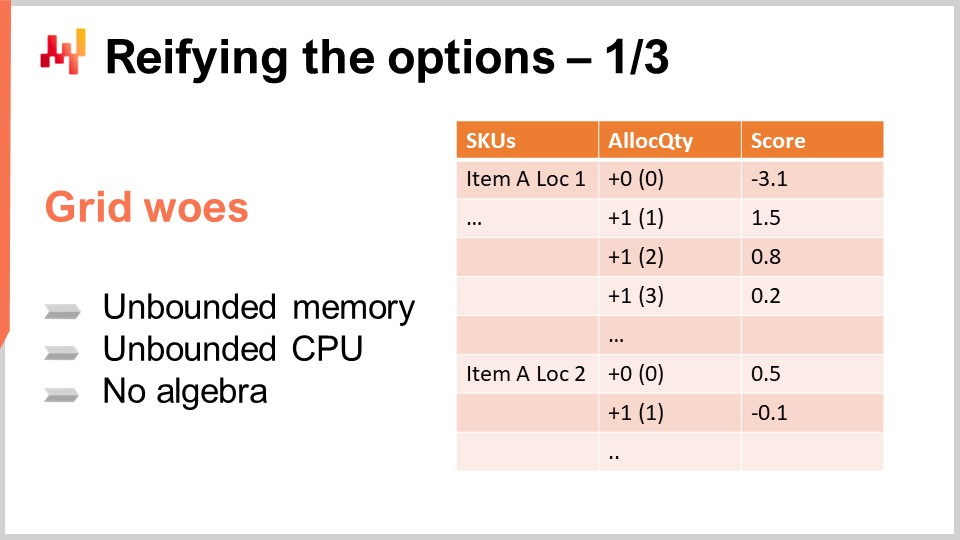
確率的予測が整ったところで、次に意思決定へのアプローチ方法を考えてみましょう。まず、選択肢について検討します。選択肢とは潜在的な意思決定そのものであり、例えば、ある製品を特定の日に特定の店舗に0ユニット、1ユニット、2ユニット、または3ユニットを配分するというものです。もし2ユニットを配分することに決めたなら、それが意思決定となります。選択肢とは、これから決定される全ての項目のことです。
これらの選択肢を整理するシンプルな方法は、画面に示されているようにリストにまとめることです。このリストは複数のSKUを網羅しており、各SKUごとに選択肢として1行ずつ追加されます。各選択肢は、配分される数量を表しています。0、1、2、3…といった具合に設定可能です。実際には無限に続ける必要はなく、配送センターの在庫数で上限を設けることができます。より現実的には、通常、製品の店舗内最大棚容量などの下限も存在します。
つまり、全SKUを含むリストがあり、各SKUごとに配送センターからの配分候補となるすべての数量が挙げられています。スコア欄には、その配分を行った場合に期待される限界的成果が付与されています。適切に設計されたスコアは、スコアが高い順に項目を選ぶことで、小売ネットワーク全体の経済的成果を最適化することを保証します。
画面に示されている2つのSKUでは、配分量が増加するにつれてスコアが低下しており、これは多くのSKUで観察される逓減するリターンの現象を示しています。基本的に、店舗に最初の1ユニットを配置することは、2ユニット目よりもはるかに大きなリターンをもたらします。最初のユニットはほぼ常に2番目のユニットより収益性が高いのです。最初は何もないため品切れ状態にあり、1ユニット配置すれば最初の顧客の品切れは解消されます。2ユニット目の場合、最初の顧客は既に満足しているため、2人目の顧客が現れたときにのみ有用となり、経済的リターンは小さくなります。しかし、一般的には在庫が増えるにつれてリターンは逓減します。選択肢間で経済的リターンが厳密に逓減しない例外もありますが、そのケースは後の講義で再検討します。とりあえず、在庫増加に伴いリターンが厳密に逓減するという単純な状況に留めておきます。
ここで示された、すべてのSKUと選択肢が一覧できる表現は、通常「グリッド」と呼ばれます。意図としては、このグリッドをROI(投資収益率)の降順に並べ替えることです。これらのグリッド自体には問題はないものの、計算コストやメモリ使用量の面で非常に効率的ではなく、ただの大きな表以上の機能は提供しません。小売ネットワークを考えると、このグリッドは最終的に十億行にもなる可能性があります。ビッグデータは良いですが、データが小さい方が摩擦が少なく、より機敏に対応できます。大規模なデータ問題を小規模なデータ問題に変換することが、現場でのシンプルさにつながるのです。

このように、Lokadが大量の選択肢に対処するために採用した解決策の一つがzedfuncsです。このデータ型は、ranvarsと同様に、しかし意思決定の観点からのranvarの対となるものです。ranvarsがあらゆる可能な未来を表すのに対して、zedfuncsはあらゆる可能な意思決定を表します。ranvarsが確率を表現するのに対して、zedfuncは一次元離散の選択肢に関連する全ての経済的成果を表現します.
The zedfunc、または zedfunction は、技術的には、正の整数と負の整数の両方を実数に写像する関数です。これは技術的な定義です。しかし、ranvars と同様に、有限のメモリで任意の複雑な関数、すなわち zedfunc を表現することは不可能です。この場合、精度と解像度との間で妥協をする必要もあります.
サプライチェーンマネジメントにおいては、任意に複雑な経済関数は存在しません。かなり複雑なコスト関数は存在し得ますが、それも任意に複雑というわけではありません。実際、zedfunc は 4 キロバイト以下に圧縮することが可能です。これにより、全体のコスト関数を表すデータ型を得つつ、数値近似の誤差がサプライチェーンの観点から無視できる程度に保たれ、常に 4 キロバイト未満に圧縮されます。最終的な(離散的な)決定に影響を及ぼさないほど数値近似を小さく保てば、たとえ無限の精度があったとしても、最終的に同じ結果になるので、その数値近似は完全に無意味と言えるでしょう.
4 キロバイトを使用する理由はコンピューティングハードウェアに関連しています。サプライチェーンマネジメント向けの現代のコンピュータハードウェアに関する以前の講義で見たように、ワークステーション、ノートブック、またはクラウド上のコンピュータであっても、最新のコンピュータのランダムアクセスメモリ (RAM) はバイト単位でのアクセスを許しません。RAM にアクセスするとすぐに、4 キロバイトのセグメントが読み出されるため、ハードウェアの設計・動作に合わせてデータ量は 4 キロバイト以下に抑えるのが最善です.
Lokad が zedfunc に用いる圧縮アルゴリズムは、ranvars で使用されるものとは異なります。なぜなら、同じ数値問題に対処しているわけではないからです。ranvars では、連続するセグメントの確率の質量を保持することが主な関心事ですが、zedfunc では焦点が異なり、位置から位置へと観測される変動量を保持することが通常求められます。なぜなら、その変動をもって最終的に利益が得られる選択肢か、あるいはプロセスを終了すべきかを判断できるからです。したがって、圧縮アルゴリズムも異なっています.

画面上には、在庫ユニット数に依存する想定保管コストを反映した zedfunc のプロットが表示されています。zedfunc は関数に関連付けられる古典的なベクトル空間と同様に、ベクトル空間の利点(加算・減算が可能)を享受します。メモリの局所性を保持することで、特定のデータ構造によって選択肢間の局所性を捉えることなく、非常に大きなテーブルを用いる単純なグリッド実装と比べ、一桁高速な操作が可能となります.
前のスライドでご覧になったプロットはスクリプトによって生成されました。1 行目と 2 行目では、2 つの線形関数 f と g を宣言しています。関数 “linear” は標準ライブラリの一部であり、“linear of one” は単なる恒等関数、つまり 1 次の多項式です。関数 “linear” は zedfunc を返し、zedfunc に定数を加えることも可能です。我々は、1 次の多項式である f と g の 2 つを持っています。3 行目では、f と g の積を通じて 2 次の多項式を構築します。5 行目から 10 行目は、zedfunc をプロットするための定型的なユーティリティです.
ここで、zedfunc と経済的成果を格納するためのデータコンテナが整いました。zedfunc は、ranvar が確率的予測のために果たしていた役割と同様のデータコンテナです。しかし、これら経済的成果を計算するための数値的手法がまだ必要です。データコンテナはあるものの、どのように経済的成果を計算し zedfunc に反映するかはまだ説明していません.

在庫報酬関数は、確率的予測と短い一連の経済的要因を考慮して、単一 SKU の各在庫レベルに対する経済リターンを計算するための小規模なフレームワークです。歴史的に、Lokad では我々の実践を統一するために在庫報酬関数が導入されました。2015 年には、Lokad はすでに確率的予測に数年間取り組んでおり、試行錯誤を通して有用な数値的手法の一連を見出していました。しかし、それらは統一されておらず、やや混沌としていました。在庫報酬関数は当時の知見をすっきりと、簡潔なミニマリスティックなフレームワークにまとめ上げました。2015 年以降、より優れた手法が開発されていますが、それらはまたより複雑です。明瞭さのため、まずは在庫報酬関数から始め、この関数を先に紹介するのが良いでしょう.
在庫報酬関数は、本質的には確率的予測に付随する経済的成果を計算する数値的手法を見つけ出すためのものです。在庫報酬関数は画面上に示されている式に従い、手元在庫 k に対して時刻 t で得られる経済リターンを定義します。変数 R は、ドルやユーロなどの単位で表現される経済リターンを示します。この関数は時刻 (t) と在庫 (k) の2変数を持ち、あらゆる在庫レベルに対する報酬を計算することを目的としています.
考慮すべき経済変数は 4 つあります:
M は販売された各ユニットあたりの粗利益です。1 ユニットを確実にサービスすることで得られる利益を意味します. S は品切れペナルティで、顧客へのサービス提供に失敗するたびに発生する一種の仮想的なコストです。たとえ顧客にペナルティを支払わなくても、適切なサービスが提供できなかったことに伴うコストが存在し、このコストはモデル化されるべきものです。最も単純なモデル化方法の一つは、サービスを提供できなかった各ユニットにペナルティを課すことです. C は保管コスト、すなわち各ユニットあたりの期間ごとのコストです。もし 1 ユニットを 3 期間在庫すれば 3 倍の C、2 ユニットであれば 6 倍の C となります. Alpha は将来のリターンを割引するために使用されます。遠い未来の出来事は、近い未来に起こる出来事ほど重要ではないという考えに基づいています. 在庫報酬関数は、過度に単純化することなく、できるだけシンプルな設計となっています。この式は、需要が在庫を上回る場合、リターンに我々が保有する全在庫分の利益が含まれることを示しています.
これは最初の行で述べている内容です。すなわち、k 個分の利益があるので、在庫中の全ユニットを販売し、その後、サービス提供できなかったユニットに対して Y(t) - k のペナルティが課せられます.
それ以外の場合、在庫が需要を上回っているときは、本日販売分の利益を表す Y(t) × M の恩恵を受けます。その後、保管コストを支払わなければなりません。本日の保管コストは日末に残る在庫 (k - Y(t)) に C を掛けたものに、さらに翌日の在庫報酬関数 R* に alpha を掛けたものとなります.
R* には注意点があります。これは在庫報酬関数 R とほぼ同一ですが、品切れペナルティのみがゼロに設定されています。その理由は単純で、在庫の観点から、後で在庫を補充する機会があると仮定しているためです。本日に品切れが発生すれば手遅れとなり品切れペナルティが発生しますが、翌日に発生すると見なされる品切れペナルティは回避可能とされます.
しかし、将来、より後の期間に発生すると見なされる品切れについては、各期間ごとに補充が可能であると仮定します。したがって、後の期間に起こる品切れでは、まだ遅い再注文が可能なため、実際には品切れは発生していません。そのため、品切れペナルティはゼロとされ、再注文によって品切れを防げると期待しているのです.
時間割引係数 alpha は非常に有用で、本質的に特定のタイムホライズンを指定する必要をなくしてくれます。在庫報酬関数は有限のタイムホライズンではなく、無限大まで継続するため、1 より小さい値である alpha によって、非常に遠い未来の出来事に付随する経済的成果は極めて小さくなり無意味となります。これにより、サプライチェーンのタイムホライズンを 60 日、90 日、1 年、2 年といった恣意的なカットオフに区切る必要がなくなります.

Envision において、在庫報酬関数は ranvar を入力として受け取り、zedfunc を返します。在庫報酬関数は、確率的予測 (ranvar) を、一連の選択肢に対する推定経済リターンを格納するコンテナである zedfunc に変換する小さな構成要素です。名前が示す通り、在庫報酬関数は、在庫が 0 ユニット、1 ユニット、2 ユニット、3 ユニット…の場合に発生する各在庫状況に関連する経済リターンを示しています。zedfunc は各在庫レベルにおける経済的成果を反映し、対応する在庫レベルに結びついた経済リターンをエンコードします.
これらの zedfunc を計算するプロセスが画面上に示されています。1 行目では、単一日のモック需要としてランダムなポアソン分布を導入します。2 行目から 7 行目では経済変数を導入し、ちなみに α を 2 つ用意しています。さらにもう一つの注意点として、在庫にはラチェット効果が存在します。一度在庫が店舗に向けて出荷されると、その在庫を戻すのは通常非常に高コストとなります。これは、店舗への配分がほぼ最終決定であることを反映しています。保管コストの面では、在庫過剰の場合に実際に保管コストが発生するため、α はあまり小さくしてはいけません。この決定は取り消すことができないのです。しかし、利益に関連する α に関しては、将来の品切れに対応する他の機会があるのと同様に、後日出荷される在庫で同じ利益を生む機会もあるため、保管コスト側で起こることに比べ非常に積極的に割引する必要があります.
9 行目から 11 行目では、在庫報酬関数そのものを導入します。先のスライドで紹介した在庫報酬関数は、利益、保管コスト、品切れペナルティの 3 つの構成要素に線形的に分解できます。実際、これらは線形分離されており、Envision ではそれぞれが個別に計算されます。zedfunc は粗利益を示す係数 M を掛けることができます.
13 行目から 15 行目では、3 つの経済的構成要素を加えることで最終的な報酬が再構成されます。このスクリプトでは、zedfunc のベクトル空間が存在するという性質を活用しています。これらの zedfunc は数値ではなく関数ですが、加算が可能であり、その結果もまた zedfunc である別の関数となります。変数 reward は、これら 3 つの構成要素を合計した結果です。内部的には、在庫報酬関数の計算は固定点解析を通じて行われ、各構成要素が一定時間で処理可能です。この一定時間による計算は些細な技術的詳細に思えるかもしれませんが、大規模な小売ネットワークを扱う場合には、洗練されたプロトタイプと実際の製品グレードの解決策との違いを生み出します.

ここで、在庫配分問題に対処するために必要なすべての要素が統合されました。確率的予測を ranvar として表現し、これら ranvar を任意の在庫値に対する経済リターンを返す関数に変換する手法、そしてその経済的成果を zedfunc として容易に表現することができます。最終的に在庫配分問題に取り組むためには、次の根幹的な疑問に答える必要があります。すなわち、もし 1 ユニットしか移動できないなら、どのユニットをなぜ移動するのか?ネットワーク内のすべての店舗が流通センターの同じ在庫を巡って競合しており、流通センターから特定の店舗へ 1 ユニットを移動させる決定の質はネットワーク全体の状況に依存します。単一の店舗だけを見ることで、その決定が良いかどうかを評価することはできません.
例えば、既に 2 ユニットの在庫がある店舗があり、3 ユニット目を追加すれば、期待されるサービスレベルが 80% から 90% に向上すると仮定しましょう。これは良いことであり、ネットワーク内の他の店舗も、サービスレベルが 80 から 90 に上がるために追加 1 ユニットを導入するという考えに同意するかもしれません。それは非常に理にかなっていますので、彼らはこれを良い動きだと判断するでしょう。しかし、もしこれから移動させようとしているこの 3 ユニット目が、実は流通センターに残る最後のユニットであった場合はどうでしょうか?ネットワーク内の別の店舗が既に品切れに苦しんでおり、このユニットを3 ユニット目として移動させると、同じ商品の品切れ状態にある店舗の品切れ状態が長引くことになります。この状況では、品切れ状態にある店舗へユニットを移動させる方が確実に良い判断となり、より高い優先順位を与えるべきです.
そのため、SKU 単位で在庫レベルを経済的に評価するのは意味がありません。局所最適化の問題点は、大規模なシステムで運用する場合には通用しないということにあります。サプライチェーンでは、局所的に対処すると、単に問題を先送りするだけで、本質的な解決には至りません。SKU の在庫レベルの適正性は、ネットワーク全体の状態に依存しているのです。この単純な例は、安全在庫や リオーダー・ポイント の計算が、少なくとも実世界の状況においては、サプライチェーンの教科書で見られる模型例と比べてほとんど無意味である理由を明確にしています.
ここでは、本当にすべての在庫配分を相互に優先順位付けしたいと考えており、最も高い評価を得た選択肢が疑問に対する答え、すなわち、もし 1 ユニットしか移動できないならそれが移動すべきユニットとなります.

在庫割り当てオプションのランク付けは、適切なツールがあれば比較的簡単です。ここで、このEnvisionスクリプトを確認しましょう。1行目では、A、B、Cという名前の3つのSKUを作成します。2行目では、1から10までのランダムな購入価格をモックデータとして生成します。3行目では、各SKUに対する報酬を表すべきモックのzedfuncを生成します。実際には、zedfuncは在庫報酬関数を用いて計算されるべきですが、コードを簡潔にするためにここではモックデータを使用しています。報酬は、在庫レベル6でゼロになる減少する線形関数です。4行目では、在庫レベルを表すグリッドの略称であるテーブルGを作成します。10を超える在庫レベルは評価する価値がないと仮定しています。この仮定は合理的です。なぜなら、モックデータでは在庫レベル6を超えると報酬関数がマイナスになるからです。6行目では、在庫内の任意のユニットに対する限界報酬を抽出し、このグリッドテーブルを作成します。報酬を表す関数であるzedfuncを使用して、在庫位置G.Nの値を抽出しています。なお、6行目以降は、データがもともとどのように生成されたかは問題になりません。1行目から4行目は本番環境では使用されないモックデータですが、6行目以降は本番環境でも実質的に同じ扱いになります。
7行目では、スコアを、(zedfuncが示す)リターンのドルと、投資されたドルである購入価格との比率として定義します。1ユニットあたりに支払う金額に対して返ってくるドルの額の比率を求めています。つまり、最も高いスコアは、1ドルあたりのリターン率が最も高い在庫割り当てに対して得られるのです。
最後に、9行目から15行目では、スコアが高い順に並べ替えたテーブルを表示します。スクリプトには華麗なロジックはなく、最初の4行は単なるモックデータの生成、最後の6行は優先順位付けされた割り当ての表示にすぎません。一度zedfuncが存在し、各在庫レベルにおける経済的リターンを表す関数が整えば、それらのzedfuncを優先順位リストに変換するのは完全に簡単です。

画面上では、先ほどのEnvisionスクリプトを実行して得られたテーブルにより、SKU Cが1位にランク付けされていることが示されています。すべてのSKUは最初のユニットに対して同じ経済リターン、すなわち5ドルのリターンを持っています。しかし、Cの購入価格は3.99ドルと最も低いため、5ドルの報酬を3.99ドルで割ると約1.25というスコアになり、これがグリッド上で最も高いスコアとなります。Cの第2ユニットは約1のスコアを持ち、これが2番目に高いスコアになります。
グリッドの3番目の位置には、別のSKUであるBがあります。Bは購入価格が高いため、最初のユニットのスコアは0.96に過ぎません。しかし、SKU Cに最初の2ユニットを割り当てた際の逓減するリターンにより、Bの最初のユニットはCの3番目のユニットよりも高いスコアとなり、その結果、BがCの3番目のユニットより上位にランク付けされます。本質的に、この優先順位リストは非常に深く掘り下げられますが、しきい値によって切り詰められることを意図しています。例えば、最小限の投資回収率を設定し、その投資回収率を上回るユニットのみを割り当てると決定できます。一度しきい値が定義されると、カットオフを上回るすべての行を取り、SKUごとに行数をカウントします。これにより、各SKUに割り当てるべきユニットの総数が得られます。このカットオフの問題には後ほど再び触れますが、基本的な考え方は、しきい値が決まればSKUごとにカウントを集計し、それが各SKUに割り当てるべき総数量となるということです。これは、流通センターに存在するWMSやERPが、翌日の店舗への出荷を整理する際に期待するものと全く同じです。
優先順位リストは、何が優先されるべきかを決定するための概念的なビューに過ぎません。しかし、しきい値を設定して集計すれば、最終的には小売店舗ネットワークに存在する各SKUごとの割り当て数量に戻ります。
優先順位付けされた在庫割り当ての表示は、一見シンプルですが非常に強力です。1行から次の行へと進むにつれて、割り当てオプション間の競争が展開する様子が見て取れます。最良のSKUが最初に割り当てられますが、在庫レベルが高くなると、在庫が少ない他のSKUに比べて競争力が低下します。こうして優先順位リストはSKU間で切り替わり、店舗に割り当てられる資本に対する期待リターンを最大化します。
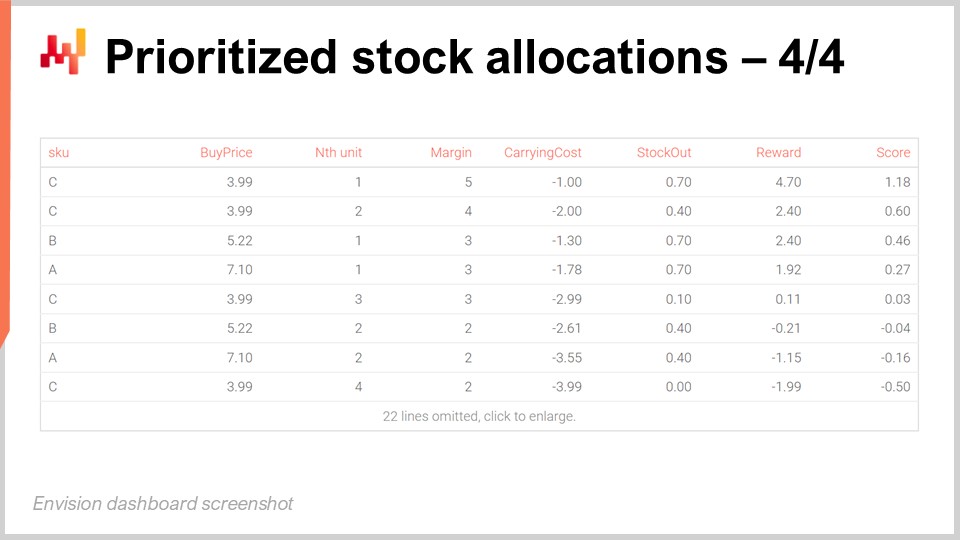
この画面では、2スライド前に紹介したものの最小限のバリアントである別のEnvisionスクリプトを用いて得られた、前のテーブルの変形版を示しています。基本的には、報酬に寄与する経済的要因を分解しています。ここでは、追加の3つの列、すなわち、マージン、保管コスト、在庫切れがあります。マージンは、割り当てられる1ユニットあたりの予想平均粗利益を示します。保管コストは、その1ユニットを店舗の在庫として保持する際の予想平均コストです。在庫切れは回避されるべき予想ペナルティであり、したがって在庫切れペナルティはここでは正の値となっています。最終的な報酬は、この3つの要素の合計であり、すべての値はドルなどの通貨単位で表現されています。マージンドル、保管コストドル、在庫切れドル、および報酬の各列は、その1ユニットを店舗に投入することで期待される総ドル額を示しています。
これにより、ドルで表現されたこの数値レシピの理解とデバッグが、パーセンテージで表す場合と比べて格段に容易になります。実際、どんな非自明な数値レシピも、その設計上、かなり不透明になりがちです。深い不透明性を得るためにディープラーニングは必要ありません。たとえ控えめな線形回帰であっても、いくつかの要因が絡むと十分に不透明になるのです。このような不透明性は、どんな非自明な数値レシピでも共通しており、サプライチェーンの現実世界において、担当者がモデル化の技術的な細部に迷い、混乱し、気を散らされる原因となります。
経済的要因を分解する優先順位付けされた割り当てリストは、強力な監査ツールです。これにより、サプライチェーン担当者は技術的な細部に翻弄されることなく、基本に直接疑問を呈することができます。例えば、「現状を踏まえて保管コストは理にかなっているのか?」「そのコストは、我々が負っているリスクと整合しているのか?」といった質問を直接投げかけることができます。予測や季節性、季節性のモデル化方法、減少傾向の要因の組み込みなどは無視して構いません。最終的な結果、つまりこれらの保管コストに対するドルで表されたアウトプットを直接問いただせるのです。本当に妥当なのか?意味が通じるのか?非常に頻繁に、意味不明な数字を見つけ出し、即座に修正することが可能です。
もちろん、こうした状況は避けたいものですが、サプライチェーンのすべての問題が非常に微妙な予測問題であると仮定してはなりません。ほとんどの場合、問題は過酷です。例えば、データが正しく処理されなかった場合など、何らかの問題が発生し、その結果、負のマージンや負の保管コストなど全く意味不明な数字が生じ、サプライチェーンに大混乱をもたらすことがあります。
もしサプライチェーンのインストゥルメンテーションが需要予測精度のみに専念しているなら、実際の問題の90%以上(大規模なサプライチェーンではおそらく99%)を見落としていることになります。サプライチェーンのインストゥルメンテーションは、意思決定に寄与する主要な要因を浮き彫りにするために絶対不可欠であり、企業を収益化させる要因に集中するためには、これらの要因が経済的なものでなければなりません。さもなければ、パーセンテージで運用すると、自分たちの行動に優先順位をつけることができず、結果として些細な不具合に無差別に対処することになるのです。大規模なサプライチェーンでは、常に膨大な数の数値的不具合が存在します。これらすべてに無差別に対処すると、実質的に重要でない事柄に常に取り組むことになってしまいます。だからこそ、リターンとコストをドルで示す必要があるのです。そうすれば、数値レシピに対する作業や開発努力に実際の優先順位を付けることができるのです。場合によっては、不具合が修正に値するかどうかを判断する必要すらなく、もし年間で数ドル分の摩擦に過ぎないのであれば、実際には修正に値する不具合ではないのです。
さて、割り当てリストの適切なカットオフを選定する問題に戻りましょう。店舗SKUにより多くの在庫を割り当てる際に、ほぼ逓減するリターンがあることがわかりました。しかし、見るべきは単に倉庫やディストリビューションセンターだけではなく、サプライチェーン全体です。ここでは、倉庫とディストリビューションセンターという用語を同じ意味で使用しています。倉庫またはディストリビューションセンターは固定費が支配的です。確かに、臨時労働者でスタッフを増強することは可能ですが、コストがかかる傾向にあり、さらに臨時労働者は通常、常勤のスタッフよりも資格が低いといった問題も発生します。
したがって、どの倉庫やディストリビューションセンターにも、経済効率が最高潮に達する目標容量があります。この目標容量は増減可能ですが、通常は常勤スタッフの規模調整を伴うため、プロセスは比較的遅いものとなります。倉庫は四半期ごとに目標容量を調整することは期待できますが、ピーク効率が発揮される名目上の容量を日々調整することは期待できません。それほどダイナミックではありません。
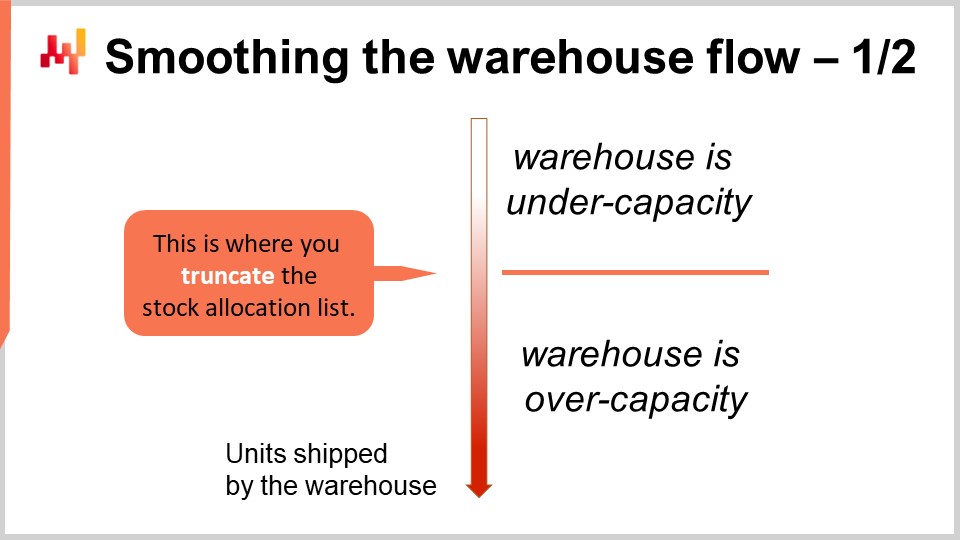
我々は、特段の経済的インセンティブがない限り、倉庫を常にピーク効率、またはできるだけピークに近い状態で運用し続けたいと考えています。優先順位付けされた在庫割り当ての視点は、まさにその実現への道を切り開きます。リストを少し短くまたは長くしてカットオフを微調整することで、倉庫の目標容量と一致させることができます。実際、これには3つの大きな利点があります。
第一に、倉庫内のフローの平準化です。これにより、倉庫はほとんどの場合、ピーク容量で運用され、多くの運用コストを節約できます。第二に、在庫割り当てプロセスは、実際のサプライチェーンで頻発する様々な小さな事故に対して、よりレジリエントになります。トラックが軽微な交通事故に巻き込まれたり、スタッフが病気で出勤しなかったりと、計画を乱す小さな理由は山ほどあります。それが倉庫の運用を完全に止めるわけではありませんが、予定していた容量で正確に運用されない可能性があります。この優先順位リストを用いれば、倉庫が実際に稼働しているどんな容量でも最大限に活用することができるのです。
第三の利点は、この在庫割り当ての優先順位リストのアプローチにより、サプライチェーンチームがもう倉庫スタッフのレベルを細かく管理する必要がなくなる点です。小売ネットワークの販売速度に大まかに合わせるために、倉庫の目標容量を調整するだけで十分であり、日々の容量を細かく管理する必要はほとんどなくなります。
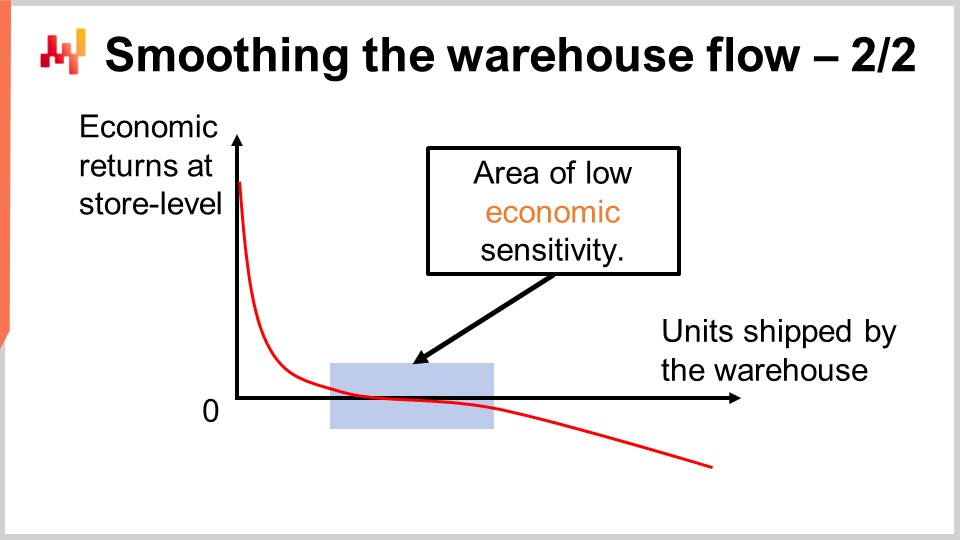
Lokadの経験では、フラットな容量カットオフを通じて倉庫内のフローを平準化する方法が、ほとんどの小売状況でうまく機能することが示されています。画面上には、あらゆるカットオフを考慮した際に観察される典型的な経済リターン曲線が表示されています。X軸には、倉庫から出荷されるユニット数が示されています。各ユニットの限界寄与を観察できるように、概念的にはユニットが1つずつ出荷されると仮定しています。もちろん、本番環境ではユニットは一括で出荷されますが、これは単に曲線をプロットするための仮定です。Y軸には、店舗レベルでの限界経済成果、すなわちネットワーク内の任意の店舗に出荷されるn番目のユニットに対する成果が示されています。最初に割り当てられるユニット群がリターンの大部分を生み出します。実際、リストのトップは常に、即時解決が求められる在庫切れの状況で構成されます。これが、最初のユニットが在庫切れに対処し、経済リターンが非常に高い理由です。その後、リターンは徐々に減少し、曲線は平坦な領域に入ります。
この領域は、私が「低い経済感度の領域」と呼ぶ部分です。本質的には、サービスレベルを徐々に100%に近づけていますが、過剰な死蔵在庫はまだ生み出していません。このような優先順位に基づく割り当てを行うと、在庫切れの問題への対処を超えて在庫を押し進めることで、ファストムーバーに在庫が山積みになってしまいます。現時点で正確に必要とされていない場所に在庫を抱えることになり、将来的には在庫切れに悩まされることなく在庫補充の機会は訪れるものの、在庫が比較的速やかに売れるため影響は最小限にとどまります。本質的には、これは流通センターから店舗へ在庫を移動させる際の機会費用の問題に他なりません。在庫をさらに割り当てるにつれて、将来の選択肢を徐々に失っていくのです。
この領域は比較的平坦ですが、在庫を過剰に押し進め、不測の在庫償却が発生する可能性が無視できない状況になると、著しくネガティブになり始めます。さらに在庫を押し進めると、より深刻な過剰在庫の状況が生じ、結果として曲線は大きくマイナスになります。あまりにも在庫を押し進めると、将来的に大量の在庫償却が発生するでしょう。カットオフがこの低感度領域内にある限り問題はなく、カットオフの位置に極端な敏感さはありません。これが、倉庫の容量が日々の販売量を直接模倣する必要がない理由です。
実際、ほとんどの小売ネットワークでは、売上において一週間の曜日別の非常に強い周期パターンが観察されます。例えば、土曜日は最も多く売れる日ですが、倉庫がこの曜日別の周期パターンを正確に模倣する必要はありません。非常に均一な平均値を維持できるので、ターゲット容量は店舗ネットワーク全体の売上高にほぼ一致すれば十分です。もしターゲット容量がネットワーク全体の売上高を常に少し下回っている場合、最初は各店舗の在庫が徐々に枯渇し、その後大きな問題に直面するでしょう。逆に、毎日実際の売上よりも少し多く供給してしまうと、すぐに各店舗が完全に飽和してしまいます。
バランスを大きく崩さなければ、曜日ごとのパターンを細かく管理する必要はなく、問題なく機能します。曜日パターンの細かい管理が不要なのは、最初の単位が大部分のリターンをもたらすためであり、カットオフがほぼ平坦なセグメント内にある限り、経済的観点からシステムがそれほど敏感でなくなるからです。

さて、明確さと簡潔さを期して在庫報酬関数を提示しましたが、今回の講義では既に多くの内容を扱っていたためです。しかし、在庫報酬関数はサプライチェーン科学の頂点ではなく、確率予測の細かな点に関してはやや単純すぎる面があります。
2021年に、Lokadのメンバーの一人がアクション報酬関数を発表しました。いわば、アクション報酬関数は在庫報酬関数の精神的子孫ですが、この関数は確率予測そのものに対して、より細分化された視点を提供します。実際、すべての確率予測が同じではありません。季節性、変動するリードタイム、そして流通センターへの入庫ETAなどが、在庫報酬関数では考慮されなかったのに対し、アクション報酬関数ではすべて考慮されています。
ちなみに、これらの機能はより細かい予測を必要とするため、そのような確率予測をすべて生成できる優れた予測技術が求められます。この点では、在庫報酬関数の方が要求が低いのです。概念的には、アクション報酬関数は発注頻度(どれだけ頻繁に発注するか)と供給リードタイム(発注後、在庫が補充されるまでの時間)を明確に切り離しており、これら二つの要素は在庫報酬関数では一体化されていましたが、アクション報酬関数では明確に分離されています。
さらに、アクション報酬関数は意思決定の所有権という視点も備えており、これはポリシーを導入せずとも、実際のポリシーから得られるほとんどの利益を享受するための、シンプルながらかなり巧妙な手法です。技術的な観点からポリシーが実際に何を意味するのかについては後の講義で議論しますが、結局のところ、ポリシーを導入し始めると物事はより複雑になるということです。興味深い話ではありますが、確かに複雑です。ここでのアクション報酬は、ポリシーに頼らずとも、その経済的利益の大部分を享受できるという巧妙な工夫がされています。

在庫報酬関数と、その優れた代替手段であるアクション報酬関数は、Lokadで何年にもわたり実運用されてきました。これらの関数は、さもなければ小売ネットワークを悩ませる一連の問題を本質的に簡素化します。例えば、店舗に既に存在する各在庫ユニットに付随する経済リターンを見るだけで、死蔵在庫の評価が容易になります。しかし、今日触れていない視点が山ほど存在します。これらの側面については、後の講義で取り上げる予定です。
今日ご紹介した内容を若干変更するだけで対処できる視点もあります。例えば、ロット乗数や在庫リバランスです。今日示したスクリプトにほんの少しの変更を加えるだけで、これらの問題に取り組むことが可能です。ここで言う在庫リバランスとは、特定の輸送コストを前提として、在庫を流通センターに戻すか、または店舗間で直接移動させることで、店舗ネットワーク内の在庫のバランスを取ることを意味します。
次に、もう少し手間はかかるが比較的単純な視点もあります。例えば、機会費用、一定の輸送コスト、そして店舗の受入過多を考慮する場合です。店舗スタッフが受け取ったすべてのユニットを処理できず、その結果、ある日に棚に陳列する時間が足りず、店舗内が大混乱に陥ることがあります。これらの視点にも対処できますが、今日示した内容に加えてかなりの作業が必要となるでしょう。
さらに、マーチャンダイジングや店舗全体の魅力向上といった、優先順位の一部として取り上げるべき視点も存在します。これらには、今日示したような軽微な変更では到底不十分な、より高度な技術的アプローチが必要です。例によって、専門家が最適な方法を持っていると主張する際には、健康的な懐疑心を持つことをお勧めします。サプライチェーンにおいて最適な方法というものは存在せず、私たちは単なるツールを持っているに過ぎません。中には優れているものもありますが、いずれも最適と呼ぶには程遠いのです。
結論として、誤差のパーセンテージは重要ではなく、重要なのは金額です。その金額は、サプライチェーンが物理的レベルで何をしているかによって決まります。ほとんどのKPIは、最良でも些細なものであり、サプライチェーン意思決定を導く数値レシピを継続的に改善するプロセスの一部に過ぎません。しかし、数値レシピを直接改善し、サプライチェーンの結果を直ちに向上させる場合と比較すると、その効果はかなり間接的です。
Excelシートはサプライチェーンにおいて至る所で使用されています。これは、主流のサプライチェーン理論が意思決定を第一級の市民として取り扱うことに失敗したためだと思います。その結果、企業は時間やお金を浪費し、第二級の市民、すなわちアーティファクトに注力することになります。しかし、最終的には意思決定が下されなければならず、在庫配分、価格選定、販売ポイント、さらには攻撃的な価格設定などを決める必要があります。適切な支援がないと、サプライチェーンの実務者は意思決定を第一級の市民として扱うことを可能にする唯一のツール、すなわちExcelに頼らざるを得なくなります。
しかし、サプライチェーンの意思決定を第一級の市民として扱うことは可能であり、これこそが本日行ったことです。現代のサプライチェーンにおける典型的なアプリケーション環境の複雑さを考えれば、ツール自体はそれほど複雑ではありません。さらに、適切なツールがあれば、流通センターから店舗への在庫の流れを最小限の労力でスムーズにするなどの機能を引き出すことができます。これらの機能は適切なツールによって容易に達成でき、少なくとも運用レベルの環境ではExcelスプレッドシートでは到底期待できない成果を示しています。

本日はこれで終わりにしたいと思います。次回の講義は7月6日水曜日、パリ時間午後3時に行われます。第7章では定量的サプライチェーン施策の戦術的実行について議論します。ちなみに、後の講義では第5章の確率予測と第6章の意思決定技術についても再度触れる予定です。特定のテーマに深く踏み込む前に、すべての要素について包括的かつ入門者向けの視点を持つことが私の目標です。
では、ここで実際に質問を見てみましょう。
質問: zedfuncは無限の可能性を持ち得ます。その場合、すべての解が短期的なものにならないでしょうか?
zedfunctionは、文字通り一連のオプションを格納するデータコンテナであり、適用される時間軸は私がスクリプトで使用したアルファ値、すなわち時間割引値に組み込まれています。本質的に、zedfunctionの経済的成果に組み込まれている目標時間軸はzedfunction自体には存在せず、それを構成する経済計算の中にあるのです。zedfunctionは単なるデータコンテナであることを忘れないでください。それが短期的か長期的かを決定づける要素であり、当然ながら数値レシピもあなたの優先順位に合わせて調整すべきです。例えば、もしあなたの会社がキャッシュフローの問題で大きなストレス下にあるなら、資金の流入を急ぐ、つまり在庫の清算に走るといった、より短期的な視点を取るでしょう。逆に、現金に余裕があれば、販売を後回しにしてより良い価格で売り、より高い粗利益を確保するという選択が可能です。改めて、これらすべてのことがzedfunctionを用いれば可能になるのです。zedfunctionは単なるコンテナであり、望む経済的成果のための特定の数値レシピを必ずしも前提とするものではありません。
質問: ほとんどの仮定は、目的関数の既存の実数値に基づくべきだと思いませんか?
実際のものとは何でしょうか?これは、実験的最適化についての講義で取り上げた問題の本質です。値や測定結果があると言っても、実際にあるのは数学的あるいは数値的な構造に過ぎません。数値であるからといって正しいとは限りません。私のサプライチェーンへのアプローチは実験科学として行われるべきであり、実世界とつながらなければなりません。つまり、仮定はあらかじめ存在する実数値に基づくものではなく、そういった実数値というものは存在しないので、必ず検証され、サプライチェーンで観測できる実際のデータと照らし合わせて挑戦されなければならないのです。あなたの仮定が正しいかどうかは、サプライチェーンの現実との接触を通じてのみ評価されます。
ここで実験的最適化の視点は厄介になります。なぜなら、数学的最適化の視点は、すべての変数が既知であり、すべての変数が実数で、すべての変数が観測可能で、損失関数が正しいと仮定するからです。しかし、私が主張しているのは、サプライチェーンは非常に複雑なシステムであり、実際にはほとんどの場合、間接的な測定値しか得られないということです。私が在庫水準と言う際、実際に店舗に足を運んで在庫が正しいか確認しているわけではなく、非常に間接的な測定、つまり、かつてデータサイエンスのためではなく何らかの理由で約20年前に導入されたenterprise softwareシステムから得た電子記録を利用しているのです。これが言いたいことです。サプライチェーンは常に地理的に分散しているため、測定するすべてのデータは間接的なものであり、これらの測定の現実性は常に疑問視されるのです。直接観測というものは存在せず、管理やチェックのために直接観測を行ったとしても、それはサプライチェーンで操作すべきすべての値のごく一部に過ぎません。
質問: 在庫報酬関数において、マージンのような単純なパラメータに加えて、在庫切れペナルティも扱っていますが、これらの複雑なパラメータを最適化するにはどうすれば良いでしょうか?
非常に良い質問です。実際、在庫切れペナルティは実在し、そうでなければ誰も高いサービスレベルを維持しようとしないでしょう。経済的に見れば、私の知る限りのすべての小売業者が在庫切れペナルティの存在を確信しており、顧客は質の高いサービスが提供されないことを嫌います。しかし、在庫切れペナルティを「複雑」と呼ぶのではなく、複雑な問題である、つまり非常に面倒な問題であり、その困難さの一部は小売ネットワークの長期戦略に直結している点にあります。たとえば、ほとんどのクライアントにおいて、在庫切れペナルティは企業のCEOと直接議論する事項であり、経営の最上位に関わる、極めて長期的な戦略上の問題なのです。
つまり、在庫切れペナルティ自体は複雑というわけではなく、非常に高いリスクが伴う議論であるため、確かに複雑といえます。我々は何を目指すべきでしょうか?顧客をどう扱うべきでしょうか?最高の価格を提供し、サービスの質が完璧でない場合は謝罪する、という選択か、あるいは極めて低価格で何かユニークなものを提供するのか?または、新規性を追求するのか?新規性を追求する場合、新製品が常に入荷することになり、新製品が継続的に入荷すれば旧製品はフェーズアウトしていくため、在庫切れを容認せざるを得なくなるのです。これが、新規性を導入し続ける方法だからです。
在庫切れペナルティは、企業の長期戦略に直接関わるため評価が難しいものです。実際のところ、最良の評価方法は実験によるものです。ある値を選び、在庫切れペナルティ、すなわち在庫ペナルティ係数のおおよその推定値を導き出し、その上で各店舗でどのような在庫状況が現れるかを観察します。そして、その在庫水準が理想の店舗像を反映しているか、つまり、本当に顧客に求められるものか、小売ネットワークで達成すべきものかを、人々の感覚に委ねるのです。
ご覧の通り、ここでは行ったり来たりの議論があります。通常、サプライチェーンの専門家は一連の数値を試し、経済的な結果を提示し、さらにある要因に付随するマクロ的なコストについて説明します。彼らは「非常に大きな品切れペナルティを設定することも可能ですが、注意してください。そうすると在庫配分ロジックが常に大量の在庫を店舗へ押し寄せることになる」と言うかもしれません。
特に、例えば、Eコマースの台頭により、多くの小売ネットワークは「特に専門店において、店舗での品切れに対してより寛容になった」と主張しています。基本的に、製品が欠品している場合、特にサイズといったバリエーションが不足していると、人々はEコマースでオンライン注文をするからです。店舗はまるでショールームのようになり、実際に店舗が製品販売の唯一の手段であった時に期待されたサービス品質とは大きく異なるものになります。
Question: 与えられた期間内の傾向を正しく把握するために、複合在庫報酬関数を導入することは可能でしょうか?
一体、何の傾向を理解するというのでしょうか?もしそれが需要の傾向であるならば、在庫報酬関数は確率的予測を取り込む関数です。ですから、需要にどのような傾向があっても、それは通常、需要をどのようにモデル化するかに起因します。在庫報酬関数の観点からは、確率的予測自体が傾向の有無にかかわらず、それらを既に内包しているのです。
さて、もし在庫報酬の定常的な視点に関して別のご質問があるなら、あなたの指摘は全く正しいです。在庫報酬関数は完全に定常的な視点を持っており、需要が各期間に確率的に全く同じように繰り返されると仮定しているため、傾向も季節性も存在しません。これは純粋に定常的な見方です。この場合、答えは「いいえ」となります。在庫報酬関数は非定常な需要に対応することはできません。しかし、アクション報酬関数はそれに対応可能です。これが、非定常な確率的需要に対処できるためにアクション報酬関数へ移行した動機の一つでもありました。
Question: 倉庫の容量は固定と仮定されていますが、実際にはピッキング、梱包、出荷の労力に依存します。カットオフポイントは倉庫運営の最適化によって定義されるべきではないでしょうか?
はい、もちろんです。これは、経済感度が低い領域での話ですが、あなたの優先在庫配分リストは、そのセグメント内であればカットの位置に対して非常に敏感ではありません。平均的には、どれだけ出荷し、どれだけ販売するかのバランスが取れている必要があり、それが理にかなっているのです。もし、倉庫最適化ロジックを実行した後で、ピッキング、梱包、出荷の労力や変動を考慮してカットオフを若干調整したいのであれば、それで構いません。直前の変更も可能です。この優先在庫配分リストの素晴らしい点は、出荷されるユニットの正確な範囲を、まさに直前で最終決定できるところにあります。必要なのは集計という一つの操作だけで、それは非常に迅速に行えるため、選択肢が広がります。まさにこれが、このアプローチが新たな供給網最適化のクラスを切り拓くと私が述べた理由です。定められた出荷枠に固執することなく、ピッキング、梱包、出荷の労力をその時々で再編成することが可能になるのです。
Question: 倉庫の流れを平滑化するには、生産の流れも平滑化する必要があります。この意思決定モデルはそれを考慮しているのでしょうか?
私は、必ずしも滑らかな生産フローを要求しているわけではないと言いたいです。多くの小売ネットワーク、例えば総合小売店では、大手FMCG企業から一度に大量生産された商品の発注を行っています。流通センターの運営コストの面で利益を得るために、生産フローを平滑化する必要はありません。たとえ生産が平滑でなくとも、流通センターから店舗へ出荷するだけで利益は得られます。
しかし、あなたのご指摘は全く正しいです。もし、垂直統合されたブランドで、生産施設、流通センター、店舗を自社内で完結している場合、サプライチェーン全体の最適化とフロー全体の平滑化に対する明確な関心が生じます。このネットワーク全体の最適化のアプローチは、本日私が示した内容の精神に非常に沿ったものです。しかし、真のマルチエシロンのサプライチェーンネットワークを最適化したいのであれば、今日ご紹介したものとは異なる手法が必要となります。それを実現するための多くの構成要素は存在しますが、今日提示したスクリプトを少し調整するだけでは不十分です。これは今後の講義で扱うマルチエシロンのセットアップに関する技術であり、より複雑なものとなります。
Question: 在庫報酬アプローチと期待誤差は、金融の期待値の概念を思い起こさせます。あなたの見解では、なぜこのアプローチはまだサプライチェーン分野で主流になっていないのでしょうか?
全くその通りです。この種の、真の経済的結果の分析は、金融界では長い間行われてきました。ほとんどの銀行が1980年代からこれらの計算を実施しており、さらにそれ以前は紙とペンで行われていたと考えられます。つまり、他の分野では長年にわたって行われてきた慣行なのです。
私が考えるに、サプライチェーンの問題点は、インターネットが登場するまでは、店舗や流通センターなどが地理的に分散していたことに起因します。1995年以前は、企業間でインターネットを介してデータを移動することは可能でしたが、非常に複雑でした。実現は可能でしたが、信頼性があり低コストで、すべてのデータを統合できる企業システムを持つことは稀でした。つまり、サプライチェーンは1980年代にはデジタル化されていたものの、ネットワーク化は十分とは言えなかったのです。ネットワークの要素や関連インフラは、ほとんどの企業にとって2000年以降になってから整備されたと言えるでしょう。
問題は、例えば、流通センターで業務を行っていても、ネットワーク全体からはかなり孤立していたため、倉庫管理者に高度な数値計算を行うためのリソースがなかったことです。倉庫管理者は管理すべき倉庫があり、通常は分析者ではありませんでした。そのため、インターネット時代以前に存在した、ネットワーク全体で情報が共有される前の慣行が引き続き行われてきたのです。それが理由であり、なおかつサプライチェーンは非常に大規模で複雑なものであるため、変化するスピードも遅いのです。
非常に優れたデータレイクを用いてネットワーク全体でデータが共有されるようになったのは、例えば2010年のことであり、今から10年前の話です。私が観察するところ、一部の企業は現在動き出しており、すでに移行を果たしている企業もありますが、サプライチェーンの規模と複雑性を考えると、10年という期間は決して長いものではありません。だからこそ、この種の分析は金融分野では約40年間も既定の手法として用いられてきたのに対し、サプライチェーン分野では未だ普及途上にあるのです(少なくとも私の謙虚な意見では)。
Question: 主に誤配置コストに基づいて計算される品切れコストはどうでしょうか?
それは可能です。改めて申し上げますが、品切れコストは文字通りあなたが下す決定です。それは、あなたが顧客に対して提供したいと考えるサービスの戦略的視点を表しています。基礎となる実体はなく、あくまであなたが望むものでしかありません。誤配置コストについて言えば、実際のところ、多くの小売ネットワークが存続しているのは、忠実な顧客基盤を持っているからです。一般的な小売店であっても週に一度訪れる店舗、四半期ごとに訪れるファッション店舗、または2年に一度訪れる家具店など、人々は再来店します。長期的な顧客忠誠心を維持し、店舗でのポジティブな体験を保証するためには、サービスの質が不可欠です。通常、ほとんどの店舗において、失われた忠誠心のコストは誤配置コストをはるかに上回ります。一例として、最安値を売りにしたブランド戦略を採る小売店が挙げられます。この場合、品揃えやサービス品質を犠牲にして、何よりも低価格を優先する可能性があります。
Question: 倉庫に在庫を保持する目的は何でしょうか?それは製品を低価格に保つためか、あるいは店舗に高価格で供給するためでしょうか?
これは非常に優れた質問です。なぜ流通センターに在庫を保持する必要があるのでしょうか?すべてをクロスドッキングして直接店舗に送ってしまえばいいのではないでしょうか?
すべてをクロスドッキングする小売ネットワークも存在しますが、この方法を採用しても、サプライヤーに注文を出す時と実際に在庫を店舗に発送する時の間には遅延が生じます。特定の配分スキームを念頭に特定数量を注文することもありますが、在庫が流通センターに届いた際に、考えを変更する柔軟性があります。二日前に考えた配分スキームに固執する必要はありません。
流通センターに在庫を保持せずに単にクロスドッキングを行うことも可能ですが、その遅延のおかげで、考えを変更してやや異なる出荷指示を行うことができます。これは、例えば予期せぬ需要急増による品切れが発生した場合に有用です。品切れは望ましくないものの、それは予想以上の需要があることを示しており、一概に悪いことばかりではありません。
その他の状況では、サプライヤーとの発注制約のために倉庫に在庫を保持することが必要です。例えば、FMCG企業は週に一度しか注文を受け付けず、通常、流通センターに満載トラック分の納品を行いたがります。あなたの注文は大口かつバッチ処理となり、流通センターはその納品に対するバッファーとして機能します。また、このセンターは在庫の配分先を後から変更する選択肢も提供します。
在庫が流通センターにある限り、考えを変更することが可能です。しかし、一度特定の店舗に配分されてしまうと、それを再び倉庫に戻すための輸送コストは非常に高額になるため、避けるべきです。
ありがとうございました。次回お会いできることを願っています。今後は戦術的戦略の実行方法と、実際の企業における定量的サプライチェーン施策の立ち上げについて議論します。またお会いしましょう!