Резервный запас (страховой запас)

От Жоаннеса Вермореля, декабрь 2007 (последнее обновление в январе 2012)

Страховой запас – это метод оптимизации запасов, который определяет, сколько товара необходимо держать сверх ожидаемого спроса для достижения заданного уровня обслуживания. Дополнительный запас выполняет роль «страховочного» буфера – отсюда и название – для защиты компании от ожидаемых будущих колебаний. Формула страхового запаса зависит как от ожидаемого будущего спроса, так и от ожидаемого времени выполнения заказа. Неопределённость предполагается нормально распределённой для обоих факторов. Формула страхового запаса является универсальной во многих системах управления запасами, включая наиболее известные ERP и MRP.

Обновление, июль 2020: Подход, описанный ниже, является «учебным» в цепочке поставок, однако, к сожалению, он оказывается крайне неэффективным. В частности, ни будущий спрос, ни время выполнения заказа не распределены нормально (то есть не по Гауссу). Более того, весь подход полностью игнорирует тот факт, что все артикулы, которые могут быть заказаны или произведены компанией, конкурируют за одни и те же ресурсы. Мы настоятельно рекомендуем не использовать модели страхового запаса, когда речь идёт о реальных цепочках поставок.

Целевая аудитория: Этот документ предназначен прежде всего для специалистов по цепочкам поставок в розничной торговле или производстве. Однако он также будет полезен редакторам программного обеспечения для бухгалтерии/ERP/eCommerce, которые хотели бы расширить свои приложения функциями управления запасами.

Мы постарались свести математические требования к минимуму, однако полностью обойтись без формул не удалось, так как основная цель этого документа – быть практическим руководством по вычислению страхового запаса.

Скачать: calculate-safety-stocks.xls (таблица Microsoft Excel)

Введение

Управление запасами – это финансовый компромисс между издержками на запасы и затратами, связанными с отсутствием товара (stock-out). Чем больше запасов, тем больше требуется оборотный капитал и тем выше издержки, связанные с обесцениванием запасов. С другой стороны, недостаток запасов приводит к дефициту товаров, упущенным возможностям продаж и может прервать весь производственный процесс.

Запасы зависят, в основном, от двух факторов

Спрос за время поставки: количество товаров, которые будут израсходованы или куплены.
Время выполнения заказа: задержка между принятием решения о пополнении запасов и повторной доступностью.

Однако оба этих фактора подвержены неопределённостям

колебания спроса: поведение клиентов может развиваться довольно непредсказуемым образом.
изменения времени выполнения заказа: поставщики или транспортные компании могут столкнуться с непредвиденными трудностями.

Определение уровня страхового запаса по сути является выбором компромисса между перечисленными затратами с учётом неопределённостей.

Соотношение издержек на запасы и затрат, связанных с отсутствием товара, сильно зависит от специфики бизнеса. Поэтому вместо прямого анализа этих затрат, мы введём классическое понятие уровня обслуживания.

Уровень обслуживания выражает вероятность того, что заданный уровень страхового запаса не приведёт к дефициту товара. Естественно, при увеличении страхового запаса уровень обслуживания также повышается. При очень больших запасах уровень обслуживания стремится к 100% (то есть вероятность дефицита товара становится нулевой).

Выбор уровня обслуживания, то есть допустимой вероятности дефицита товара, выходит за рамки данного руководства, но у нас есть отдельное руководство по расчёту оптимальных уровней обслуживания.

Модель пополнения запасов

Точка повторного заказа – это уровень запасов, при достижении которого должен быть произведён заказ. Если бы не было неопределённостей (то есть будущий спрос был бы точно известен, а поставки – абсолютно надёжны), точка повторного заказа просто равнялась бы суммарному прогнозируемому спросу за время выполнения заказа, также называемому спросом за время выполнения заказа.

На практике, из-за неопределённостей, получаем

reorder point = lead time demand + safety stock

Если предположить, что прогнозы не имеют систематической погрешности (с точки зрения статистики), то отсутствие страхового запаса приводило бы к уровню обслуживания в 50%. Действительно, отсутствие смещения в прогнозах означает, что вероятность того, что будущий спрос окажется больше или меньше спроса за время выполнения заказа, равна (напомним, что спрос за время выполнения заказа – это всего лишь прогнозируемое значение).

Внимание: прогнозы могут быть несмещёнными, но не точными. Смещение указывает на систематическую ошибку модели прогнозирования (например, всегда завышают спрос на 20%).

Нормальное распределение ошибки

На данном этапе нам нужен способ описания неопределённости спроса за время выполнения заказа. В дальнейшем мы будем предполагать, что ошибка распределена нормально, что иллюстрируется на следующем изображении.

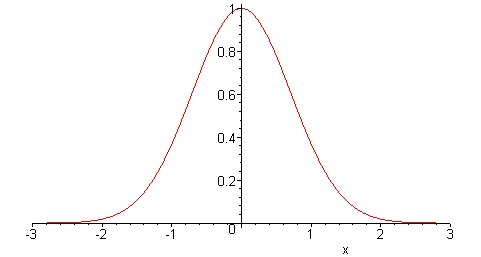
Нормальное распределение, также известное как Гауссово.

Статистические заметки: предположение о нормальном распределении не является произвольным. В определённых ситуациях статистические оцениватели сходятся к нормальному распределению, как это предписано центральной предельной теоремой. Однако эти соображения выходят за рамки данного руководства.

Нормальное распределение определяется всего двумя параметрами: средним значением и дисперсией. Поскольку мы предполагаем, что прогнозы несмещённые, мы считаем, что среднее значение распределения ошибок равно нулю, что не означает, что ошибка отсутствует.

Определение дисперсии ошибки прогноза – это более сложная задача. Lokad, как и большинство инструментов прогнозирования, предоставляет оценки MAPE (средняя абсолютная процентная ошибка), связанные с его прогнозами. Для полноты картины мы объясним, как можно использовать простые эвристики для решения этой проблемы.

В частности, дисперсия в исторических данных может быть использована в качестве хорошей эвристики для оценки дисперсии ошибки прогноза. Дэвид Пиасецки также предлагает использовать прогнозируемый спрос вместо среднего спроса в выражении для дисперсии, то есть

$$σ^2 = E[ (y_t - y')^2 ]$$

где $$E$$ обозначает оператор среднего, $$y_t$$ – исторический спрос за период $$t$$ (обычно это объём продаж), а $$y’$$ – прогнозируемый спрос.

Основная идея этого предположения заключается в том, что ошибка прогноза очень часто коррелирует с ожидаемой величиной колебаний: чем больше предстоящие колебания, тем выше ошибка прогноза.

На самом деле расчёт этой дисперсии ошибки включает несколько тонкостей, которые будут рассмотрены более подробно ниже.

Выражение страхового запаса

На данном этапе мы определили как среднее, так и дисперсию, следовательно, распределение ошибок известно. Теперь нам нужно вычислить допустимый уровень ошибки в этом распределении. Выше мы ввели понятие уровня обслуживания (в процентах) для этого.

Примечания: Мы предположили, что время выполнения заказа является статичным. Однако очень похожий подход можно использовать и для изменяющегося времени выполнения заказа. См.

Чтобы преобразовать уровень обслуживания в уровень ошибки, также называемый коэффициентом обслуживания, мы должны использовать обратную кумулятивную функцию нормального распределения (иногда её также называют обратным нормальным распределением) (см. NORMSINV для соответствующей функции в Excel). Хотя это может показаться сложным, на самом деле нет. Мы предлагаем взглянуть на апплет нормального распределения, чтобы получить более наглядное представление. Как видно, кумулятивная функция преобразует процент в площадь под кривой, а порог по оси X соответствует значению коэффициента обслуживания.

Интуитивно, мы вычисляем

safety stock = standard deviation of error * service factor

Более формально, пусть $$S$$ - это страховой запас, тогда получаем

$$S = \sigma \cdot \text{icdf}(P)$$

где $$\sigma$$ – стандартное отклонение (то есть квадратный корень из $$\sigma^2$$, дисперсии, определённой выше), $$cdf$$ – нормированная кумулятивная функция нормального распределения (со средним, равным нулю, и дисперсией, равной единице) и $$P$$ – уровень обслуживания.

Напомним, что

reorder point = lead time demand + safety stock

Пусть $$R$$ обозначает точку повторного заказа, тогда получаем

$$R = y' + \sigma \cdot \text{icdf}(P)$$

Сопоставление времени выполнения заказа и прогнозного периода

До сих пор мы просто предполагали, что для заданного времени выполнения заказа мы можем напрямую получить соответствующий прогноз будущего спроса. На практике все обстоит не так. Анализ исторических данных обычно начинается с агрегирования данных по временным периодам (обычно неделям или месяцам).

Однако выбранный период может не точно соответствовать времени выполнения заказа, поэтому требуются дополнительные расчёты, чтобы выразить спрос за время выполнения заказа и связанную с ним дисперсию (учитывая, что мы всё ещё предполагаем нормальное распределение ошибки прогноза, как подробно описано в предыдущем разделе).

Интуитивно, спрос за время выполнения заказа можно вычислить как сумму прогнозируемых значений для будущих периодов, попадающих в интервал времени выполнения заказа. При этом необходимо аккуратно скорректировать последний прогнозируемый период.

Формально, пусть $$T$$ — период, а $$L$$ — время выполнения заказа. Тогда запишем

$$L = k \cdot T + \alpha \cdot T$$

где $$k$$ — целое число и $$0 ≤ α < 1$$. Пусть $$D$$ — спрос за время выполнения заказа. Тогда окончательное выражение для спроса за время выполнения заказа выглядит следующим образом

$$ D = \sum_{t=1}^k y'_t + \alpha y'_{k+1} $$

где $$y’_n$$ — прогнозируемый спрос на $$n^{th}$$ период в будущем.

Принимая те же предположения о нормальном распределении, мы можем вычислить дисперсию ошибки прогноза как

$$\sigma^2 = E\left[ (y_t - y')^2 \right]$$

где $$y’$$ — средний прогноз по периоду

$$y' = \frac{D}{k + \alpha}$$

Однако, $$\sigma^2$$ вычислена здесь как дисперсия на период, в то время как нам нужна дисперсия, соответствующая времени выполнения заказа. Пусть $$\sigma_{L}^2$$ — это скорректированная дисперсия на время выполнения заказа, тогда получаем

$$\sigma_{L}^2 = (k + \alpha) \sigma^2$$

Наконец, мы можем переписать точку повторного заказа как

$$R = D + \sigma_{L} \cdot \text{cdf}(P)$$

Использование Excel для расчёта точки повторного заказа

В этом разделе подробно описано, как рассчитать точку повторного заказа в Microsoft Excel. Рекомендуем ознакомиться с примером Excel-таблицы, предоставленным в материалах.

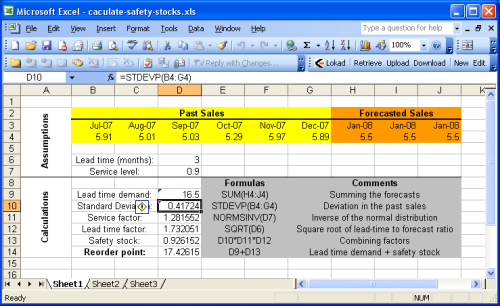
Лист Excel, иллюстрирующий формулу страхового запаса.

Пример таблицы в основном разделён на две части: предпосылки в верхней части и расчёты в нижней части. Прогнозы считаются частью предпосылок, так как прогнозирование продаж (или спроса) выходит за рамки данного руководства. Для деталей вы можете обратиться к нашему руководству по прогнозированию продаж в Microsoft Excel.

Большинство формул, приведённых в предыдущем разделе, представляют собой простые операции (сложение, умножение), которые очень легко выполнить в Microsoft Excel. Однако выделяются две функции

NORMSINV (Microsoft KB): оценивает кумулятивную функцию нормального распределения, обозначаемую здесь как cdf.
STDEV (Microsoft KB): оценивает стандартное отклонение, обозначаемое здесь как $$σ$$. Напомним, что стандартное отклонение $$σ$$ – это квадратный корень из дисперсии $${σ^2}$$.

Для простоты первый лист не реализует эвристику $${σ^2 = E[ (y_t - y’)^2 ]}$$ при вычислении коэффициента обслуживания. Этот подход реализован во втором листе (Sheet2) Excel-документа. Поскольку в примере предполагается стационарность прогнозов, точка повторного заказа остаётся неизменной с этой эвристикой и без неё.

Ресурсы

Управление запасами и планирование производства, Эдвард А. Сильвер, Дэвид Ф. Пайк, Рейн Петерсон, Wiley; 3-е издание, 1998