Функция потерь Pinball

learn menu
Автор: Жоаннес Верморель, февраль 2012 года

Функция потерь Pinball, также известная как квантильная потеря, является метрикой, используемой для оценки точности квантильного прогноза.

Оценка точности квантильного прогноза является сложной проблемой. Действительно, в отличие от классических прогнозов, где целью является максимальное приближение прогноза к наблюдаемым значениям, ситуация с квантильными прогнозами является смещенной (нарочно). Поэтому наивное сравнение наблюдаемых значений и прогнозов неудовлетворительно. Функция потерь Pinball возвращает значение, которое можно интерпретировать как точность модели квантильного прогнозирования.

Формула

Пусть $${\tau}$$ - целевой квантиль, $${y}$$ - реальное значение и $${z}$$ - квантильный прогноз, тогда функция потерь $${L_\tau}$$ (функция потерь Pinball) может быть записана следующим образом:

$${ \begin{eqnarray} L_{\tau}(y,z) & = & (y - z) \tau & \textrm{ если } y \geq z \\\ & = & (z - y) (1 - \tau) & \textrm{ если } z > y \end{eqnarray} }$$

Скачать: pinball-loss-function.xlsx

Электронная таблица демонстрирует, как вычислить функцию потерь Pinball в Microsoft Excel. Фактическая формула не сложнее большинства показателей точности, таких как MAPE.

Иллюстрация

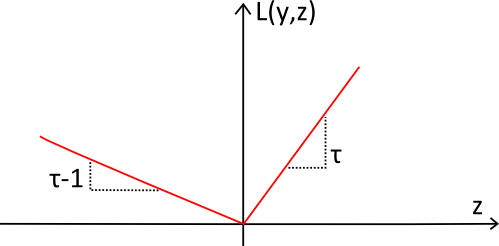
/pinball-loss-function

Функция потерь Pinball (красная линия) получила свое название из-за своей формы, которая напоминает траекторию шара на пинболе. Функция всегда положительна, и чем дальше от цели $${y}$$, тем больше значение $${L_\tau(y,z)}$$. Наклон используется для отражения желаемого дисбаланса в квантильном прогнозе.

Лучшая модель квантиля имеет наименьшую функцию потерь Pinball

Самый важный результат, связанный с функцией потерь Pinball, заключается в том, что чем ниже функция потерь Pinball, тем более точен квантильный прогноз.

Можно доказать, что функция, минимизирующая функцию потерь Pinball, также обеспечивает оптимальный квантиль. Однако формализм, необходимый для доказательства, выходит за рамки данной статьи.

Таким образом, для сравнения относительной точности двух моделей квантиля (например, Lokad против других) достаточно вычислить среднюю функцию потерь Pinball каждой модели на достаточно большом количестве временных рядов, чтобы убедиться, что наблюдаемая разница является статистически значимой. На практике достаточно нескольких сотен временных рядов, чтобы определить, какая модель квантиля является наиболее точной.

Особенность Lokad

Предполагаемая простота понятия точности для классического прогноза (т.е. среднего прогноза) в большинстве случаев преувеличена, на наш взгляд. Прогнозы, как средние, так и квантильные, подвержены переобучению, что значительно усложняет сравнение моделей прогнозирования. Однако функция потерь Pinball представляет собой очень простой способ оценки относительной точности двух моделей квантильного прогнозирования.

Дополнительная информация