Вероятностное прогнозирование (Цепочка поставок)

Прогноз считается вероятностным, а не детерминированным, если он содержит набор вероятностей, соответствующих всем возможным будущим исходам, вместо того чтобы указывать один конкретный исход как «прогноз». Вероятностные прогнозы важны, когда степень неопределенности не может быть снижена, что практически всегда имеет место при рассмотрении сложных систем. Для цепочек поставок вероятностное прогнозирование необходимо для принятия устойчивых решений в условиях неопределенного будущего. В частности, спрос и срок поставки — два ключевых аспекта анализа цепочки поставок — лучше всего решаются с помощью вероятностного прогнозирования. Вероятностная перспектива естественным образом предполагает экономическую приоритизацию решений, основанных на их ожидаемой, но неопределенной отдаче. Широкий спектр статистических моделей предоставляет вероятностные прогнозы. Некоторые из них структурно близки к их детерминированным аналогам, в то время как другие существенно отличаются. Оценка точности вероятностного прогноза требует использования специальных метрик, отличающихся от метрик детерминированных прогнозов. Использование вероятностных прогнозов требует специализированных инструментов, отличных от используемых для детерминированных прогнозов.

Детерминированные против вероятностных прогнозов

Оптимизация цепочек поставок основывается на правильном предвидении будущих событий. Эти события численно предсказываются посредством прогнозов, которые включают широкий спектр числовых методов для количественной оценки будущего. Начиная с 1970-х годов, наиболее широко используемой формой прогноза является детерминированный прогноз временных рядов: величина, измеряемая во времени — например, спрос в единицах для продукта — проецируется в будущее. Прошлая часть ряда представляет собой исторические данные, а будущая часть — прогноз.

Эти прогнозы временных рядов называются детерминированными, поскольку для каждой точки во времени они предоставляют единственное значение, которое ожидается максимально близким к будущему результату. Конечно, хоть прогноз и является однозначным, широко известно, что он вряд ли окажется абсолютно точным. Будущие результаты будут расходиться с прогнозом. Соответствие детерминированного прогноза будущим результатам количественно оценивается с помощью метрик точности, таких как среднеквадратичная ошибка (MSE).

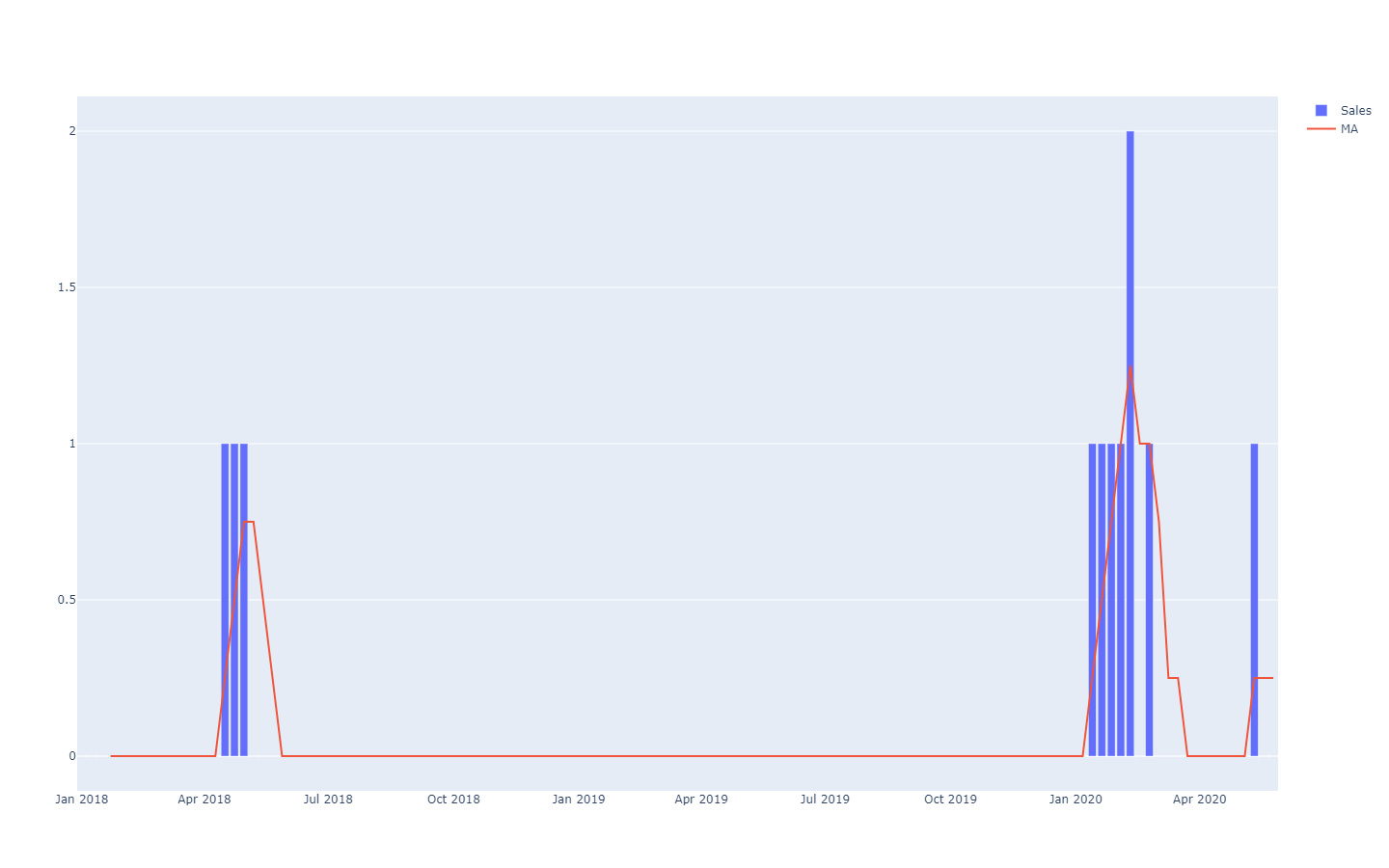
Вероятностные прогнозы принимают иной подход к предсказанию будущих исходов. Вместо того чтобы выдавать одно значение как «наилучший» исход, вероятностный прогноз заключается в присвоении вероятности каждому возможному результату. Иными словами, все будущие события остаются возможными, но имеют разную вероятность. Ниже представлена визуализация вероятностного прогноза временного ряда с эффектом «дробовика», который обычно наблюдается в большинстве реальных ситуаций. Мы более подробно рассмотрим эту визуализацию ниже.

Временной ряд, представляющий собой величину, измеряемую во времени, вероятно, является самой известной и широко используемой моделью данных. Эту модель можно прогнозировать как с применением детерминированных, так и вероятностных методов. Однако существует множество альтернативных, зачастую более богатых, моделей данных, к которым также можно применять оба вида прогнозирования. Например, компания, занимающаяся ремонтом авиационных двигателей, может захотеть предсказать точный список запасных частей, которые понадобятся для предстоящего обслуживания. Такое предвидение может принимать форму прогноза, но это не будет прогноз временного ряда. Детерминированный прогноз для этой операции представляет собой точный список деталей и их количеств, в то время как вероятностный прогноз — вероятность для каждой комбинации деталей (с учетом количеств), что именно эта комбинация окажется необходимой для проведения ремонта.

Кроме того, хотя термин «прогноз» подчеркивает аспект предвидения, эту концепцию можно обобщить на любые статистически выведенные суждения о системе, включая её прошлые (но неизвестные) характеристики. Практика статистического прогнозирования возникла в XX веке, до появления современной перспективы статистического обучения, которая охватывает все экстраполяции на основе данных, независимо от временного аспекта. Для ясности мы будем и далее использовать термин «прогноз», даже если временной аспект всегда предполагает, что прошлое известно, а будущее — нет. Например, компания может захотеть оценить продажи, которые произошли бы для продукта в магазине, если бы товар не был распродан в этот день. Такая оценка полезна для количественного определения масштабов проблемы с точки зрения качества обслуживания. Однако, поскольку событие уже прошло, «реальные» продажи никогда не будут зафиксированы. Тем не менее, если они еще не были тривиально зафиксированы, статистическая оценка прошедшего спроса является задачей, очень близкой к оценке будущего спроса.

Вероятностные прогнозы содержат больше информации, чем их детерминированные аналоги. В то время как детерминированный прогноз предоставляет «лучшее предположение» о будущем результате, он ничего не говорит об альтернативных исходах. Фактически, всегда можно преобразовать вероятностный прогноз в его детерминированный аналог, взяв среднее, медиану, моду и т.д. распределения вероятностей. Однако обратное неверно: из детерминированного прогноза нельзя восстановить вероятностный.

Тем не менее, хотя вероятностные прогнозы статистически превосходят детерминированные, они до сих пор используются редко в цепочках поставок. Однако их популярность неуклонно растет в последнее десятилетие. Исторически вероятностные прогнозы появились позже, поскольку требуют значительно больших вычислительных ресурсов. Использование вероятностных прогнозов для целей цепочки поставок также требует специализированного программного обеспечения, которое зачастую недоступно.

Сценарии использования цепочки поставок

Оптимизация цепочки поставок заключается в принятии «правильного» решения — в текущий момент времени — которое максимально эффективно решит будущую ситуацию, оцененную лишь приблизительно. Однако неопределенность, связанная с будущими событиями, в значительной степени неизбежна. Таким образом, компании необходимо, чтобы решение было устойчивым к тому, что предвидение будущего события — то есть прогноз — может быть неточным. Это минимально реализовано с середины XX века посредством анализа страхового запаса. Однако, как мы увидим ниже, помимо исторической значимости, нет причин отдавать предпочтение страховым запасам перед «нативными» вероятностными числовыми рецептами.

Перспектива вероятностного прогнозирования занимает радикальную позицию по отношению к неопределенности: этот подход стремится количественно оценить неопределенность в максимальной степени. В цепочках поставок затраты, как правило, сосредоточены на статистических экстремумах: именно неожиданный высокий спрос приводит к отсутствию запасов, а неожиданный низкий спрос — к списанию запасов. Между этими крайностями инвентарь нормально обновляется. Грубо говоря, вероятностные прогнозы представляют собой попытку управления редкими, но дорогостоящими ситуациями, характерными для современных цепочек поставок. Вероятностные прогнозы можно и нужно рассматривать как основной элемент любой практики управления рисками в цепочке поставок.

Многие аспекты цепочек поставок особенно подходят для вероятностного прогнозирования, например:

• спрос: одежда, аксессуары, запасные части, а также многие другие виды продукции, как правило, сопряжены с непредсказуемым и/или прерывистым спросом. Запуски новых продуктов могут оказаться как успешными, так и провальными. Акции конкурентов могут временно и нерегулярно отбирать значительную долю рынка.
• срок поставки: зарубежный импорт может столкнуться с целым рядом задержек на любом этапе цепочки (производство, транспорт, таможня, приемка и т.д.). Даже местные поставщики могут время от времени иметь длительные сроки, если возникает дефицит. Сроки поставки, как правило, характеризуются распределениями с «тяжелыми хвостами».
• урожай (свежие продукты): количество и качество продукции многих свежих продуктов зависят от таких условий, как погода, которая находится вне контроля компании. Вероятностный прогноз количественно оценивает эти факторы на весь сезон и дает возможность выйти за рамки временного горизонта, охватываемого классическими прогнозами погоды.
• возвраты (электронная коммерция): когда покупатель заказывает один и тот же товар в трех разных размерах, велика вероятность, что два из них будут возвращены. Более того, хотя существуют существенные региональные различия, покупатели склонны пользоваться благоприятными условиями возврата, когда они предоставляются. Вероятность возврата для каждого заказа должна быть оценена.
• списание (авиация): ремонтируемые детали самолетов — часто называемые роторными — иногда не подлежат ремонту. В этом случае деталь списывается, поскольку она больше не пригодна для повторного использования на самолете. Хотя обычно невозможно заранее узнать, удастся ли детали отремонтировать, следует оценить вероятность их списания.
• запасы (розничная торговля B2C): покупатели могут перемещать, повреждать или даже красть товары из розничного магазина. Таким образом, электронный уровень запасов является лишь приблизительной оценкой фактической доступности товаров на полках, как ее воспринимают покупатели. Уровень запасов, воспринимаемый покупателями, должен оцениваться посредством вероятностного прогноза.
• …

Этот краткий список демонстрирует, что направления, для которых применим вероятностный прогноз, значительно превосходят традиционные подходы «прогнозирования спроса». Хорошо налаженная оптимизация цепочки поставок требует учета всех существенных источников неопределенности. Хотя иногда возможно снизить неопределенность — как подчеркивает бережливое производство — обычно существуют экономические компромиссы, и, в результате, определенная степень неопределенности остается неизбежной.

Прогнозы, однако, представляют собой всего лишь обоснованные предположения о будущем. Хотя вероятностные прогнозы можно считать удивительно детальными суждениями, в этом отношении они принципиально не отличаются от своих детерминированных аналогов. Ценность вероятностных прогнозов для цепочки поставок заключается в том, как эта детализированная информация используется для принятия более прибыльных решений. В частности, от вероятностных прогнозов, как правило, не ожидается большей точности, чем от их детерминированных аналогов, если оценивать их с помощью детерминированных метрик точности.

В защиту изменчивости

Несмотря на то, что многие подходы к цепочке поставок выступают за снижение изменчивости, она останется — отсюда и необходимость в вероятностных прогнозах. Первое заблуждение заключается в том, что изменчивость обязательно является негативным явлением для цепочки поставок; это не так. Второе заблуждение — в том, что изменчивость можно устранить с помощью инженерных мер; это невозможно.

Изменчивость имеет положительные последствия для цепочки поставок в различных ситуациях. Например, на стороне спроса многие сегменты управляются новизной — мода, культурные продукты, товары мягкой и твёрдой роскоши, а также бизнесы, зависящие от случайного успеха. Большинство новых продуктов не становятся популярными (провальными), но те, что становятся хитами, приносят огромную прибыль. Дополнительная изменчивость полезна, поскольку увеличивает вероятность значительных доходов, в то время как потери ограничены (в худшем случае весь запас списывается). Постоянный поток новых продуктов, выводимых на рынок, обеспечивает постоянное обновление «хитов», в то время как старые утрачивают свою актуальность.

С точки зрения поставок, процесс закупок, обеспечивающий предложения с высокой изменчивостью цен, превосходит — при прочих равных условиях — альтернативный процесс, генерирующий гораздо более стабильные (то есть менее изменчивые) цены. Действительно, выбирается вариант с наименьшей ценой, а остальные отбрасываются. Не имеет значения, что «средняя» закупочная цена низкая; важно обнаруживать поставщиков с еще более низкими ценами. Таким образом, правильно организованный процесс закупок должен быть настроен на увеличение изменчивости, например, за счет регулярного поиска новых поставщиков вместо ограничивания процесса закупок только известными поставщиками.

Иногда изменчивость может быть полезна по более тонким причинам. Например, если бренд слишком предсказуем в своих акционных операциях, покупатели замечают закономерность и начинают откладывать покупку, зная, что акция неизбежно наступит. Изменчивость — даже нерегулярность — в проведении промо-акций в определенной степени смягчает такое поведение.

Другой пример — наличие факторов, создающих путаницу, внутри самой цепочки поставок. Если новые продукты всегда запускаются одновременно с телевизионной и радиокампанией, становится статистически сложно различить влияние телевидения и радио. Добавление изменчивости в интенсивность кампаний для каждого канала позволяет впоследствии извлечь больше статистической информации, которая затем может быть использована для более эффективного распределения маркетинговых ресурсов.

Естественно, не всякая изменчивость полезна. Бережливое производство правильно акцентирует внимание на том, что на производственной стороне цепочки поставок изменчивость обычно оказывает негативное воздействие, особенно когда речь идёт об изменяющихся задержках. Действительно, процессы LIFO (последним поступил – первым вышел) могут случайно появляться, что, в свою очередь, усугубляет изменчивость времени выполнения заказа. В таких ситуациях случайная изменчивость должна быть устранена, как правило, посредством улучшения процесса, а иногда — за счёт лучшего оборудования или инфраструктуры.

Изменчивость — даже если она оказывает негативное воздействие — часто остаётся неустранимой. Как мы увидим в следующем разделе, цепи поставок подчиняются закону малых чисел. Заблуждение полагать, что уровень магазина когда-либо сможет быть надёжно предсказан — с детерминированной точки зрения — в то время как покупатели не всегда знают, что они собираются купить. Более того, снижение изменчивости всегда сопровождается затратами (а дальнейшее снижение обходится ещё дороже), при этом предельное уменьшение изменчивости даёт всё меньшую отдачу. Таким образом, даже если изменчивость можно уменьшить, по сути, её очень редко удаётся полностью устранить из-за экономических последствий.

Закон малых чисел

Закон малых чисел в цепочке поставок можно сформулировать так: на протяжении всей цепочки преобладают малые числа. Этот наблюдательный закон является следствием эффекта экономии от масштаба и ещё нескольких факторов, которые определяют большинство структурных аспектов цепочек поставок:

• поставщик, который обеспечивает десятки тысяч единиц материалов в день, скорее всего, устанавливает минимальные размеры заказов (MOQ) или ценовые пороги, препятствующие слишком частым заказам. Количество заказов, поступающих поставщику в любой день, редко превышает однозначное число.
• завод, выпускающий десятки тысяч единиц продукции в день, обычно работает партиями по тысяче единиц. Продукция зачастую упаковывается целыми поддонами. Количество партий в течение любого дня, как правило, не превышает небольшого двузначного числа.
• склад, получающий десятки тысяч единиц в день, обычно обслуживается грузовиками, при этом каждый грузовик разгружает весь свой груз на складе. Количество грузовиков, обслуживающих склад в любой день, редко превышает двузначное число, даже для очень больших складов.
• розничный магазин, способный хранить на складе десятки тысяч единиц, обычно располагает ассортиментом из тысяч различных товарных позиций. Количество единиц, хранящихся в запасе для каждого товара, чрезвычайно редко превышает однозначное число.
• …

Естественно, изменив единицу измерения, всегда можно представить числа в завышенных значениях. Например, если вместо подсчёта количества поддонов считать количество граммов поддонов или их денежную стоимость в центах США, появляются очень большие числа. Однако закон малых чисел следует понимать с позиции разумного управления цепями поставок. Хотя в теории этот принцип может показаться довольно субъективным, на практике это не так, благодаря очевидной дискретности современных цепочек поставок: пакеты, коробки, поддоны, контейнеры, грузовики …

Этот закон имеет большое значение для вероятностного прогнозирования. Во-первых, он указывает на то, что дискретные прогнозы преобладают в ситуациях цепочки поставок, то есть ожидаемый результат (или выбранный вариант) является целым числом, а не дробным. Вероятностные прогнозы особенно подходят для дискретных случаев, поскольку для каждого дискретного исхода можно оценить вероятность. В противоположность этому, детерминированные прогнозы испытывают трудности с дискретными исходами. Например, что должно означать утверждение о том, что ожидаемые ежедневные продажи товара составляют 1.3 единицы? Товары не продаются дробно. Хотя из этого высказывания можно вывести более логичное «дискретное» толкование, его вероятностный аналог (например, 27% вероятность, что спрос составит 0 единиц, 35% — 1 единицу, 23% — 2 единицы спроса и т.д.) намного проще, поскольку отражает дискретный характер исследуемого явления.

Во-вторых, хотя может показаться, что вероятностные прогнозы требуют радикально больше вычислительных ресурсов, на практике это не так, именно благодаря закону малых чисел. Действительно, возвращаясь к обсуждаемым ежедневным продажам товара, нет смысла численно оценивать вероятность того, что спрос в любой конкретный день превысит 100. Эти вероятности можно округлить до нуля — или до какого-либо произвольно малого значения. Влияние на числовую точность модели цепочки поставок остаётся незначительным. Как правило, разумно считать, что для вероятностных прогнозов требуется примерно на три порядка величины больше вычислительных ресурсов, чем для их детерминированных аналогов. Однако, несмотря на эти накладные расходы, преимущества с точки зрения эффективности цепочки поставок значительно превосходят стоимость вычислительных ресурсов.

Метрики точности для вероятностных прогнозов

Как бы то ни было, достаточно хорошо разработанный вероятностный прогноз указывает на то, что для данного исхода действительно существовала ненулевая вероятность. Это интригующе, поскольку на первый взгляд может показаться, что вероятностные прогнозы каким-то образом не подвержены реальности, подобно гадалке, дающей крайне неоднозначные предсказания, которые никогда нельзя опровергнуть, ведь гадалка всегда может позже придумать объяснение, как правильно интерпретировать пророчества. На самом деле существует несколько способов количественной оценки качества вероятностного прогноза. Некоторые из этих способов представляют собой метрики, схожие по духу с метриками, используемыми для оценки точности детерминированных прогнозов. Другие же способы расходятся в более радикальном и глубоком направлении по сравнению с детерминированной точкой зрения.

Давайте кратко рассмотрим четыре различных подхода для оценки точности вероятностного прогноза:

• функция потерь пинбол
• функция непрерывно ранжированной вероятности (CRPS)
• байесовское правдоподобие
• генеративно-состязательная перспектива

Функция потерь пинбол pinball loss function обеспечивает метрику точности для оценки квантиля, полученного из вероятностного прогноза. Например, если мы хотим оценить такое количество запаса, которое с вероятностью 98% окажется больше или равно спросу клиента в магазине для данного товара, это количество можно получить непосредственно из вероятностных прогнозов, просто суммируя вероятности, начиная с 0 единиц спроса, 1 единицы спроса … до тех пор, пока суммарная вероятность не превысит 98%. Функция потерь пинбол loss function обеспечивает прямое измерение качества этой смещённой оценки будущего спроса. Её можно рассматривать как инструмент для оценки качества любой точки функции кумулятивной плотности вероятности вероятностного прогноза.

Непрерывно ранжированная оценка вероятностей (CRPS) предоставляет метрику, которую можно интерпретировать как «величину смещения» массы вероятностей, необходимую для переноса всей вероятностной массы к наблюдаемому результату. Это наиболее прямое обобщение средней абсолютной ошибки (MAE) в сторону вероятностного подхода. Значение CRPS имеет ту же размерность, что и единица измерения самого результата. Этот подход можно обобщить на произвольные метрические пространства, а не только на одномерные случаи, с помощью так называемой «теории транспортировки» и расстояния Монжа–Канторовича (что выходит за рамки данного документа).

Правдоподобие и его аналог по перекрёстной энтропии принимают байесовскую точку зрения минимальной степени удивления: чем выше вероятность наблюдаемых результатов, тем лучше. Например, пусть есть две вероятностные модели A и B: модель A утверждает, что вероятность наблюдения 0 единиц спроса составляет 50% для любого дня; модель B утверждает, что вероятность наблюдения 0 единиц спроса составляет 1% для любого дня. Мы наблюдаем спрос в течение 3 дней и фиксируем следующие значения: 0, 0, 1. У модели A был примерно 10% шанс сгенерировать эти наблюдения, в то время как у модели B этот шанс составляет лишь примерно 0,01%. Таким образом, модель B гораздо менее вероятно является правильной по сравнению с моделью A. Правдоподобие отличается от детерминированного подхода отсутствием осмысленного абсолютного критерия для оценки моделей. Вместо этого оно предоставляет механизм для сравнения моделей, но численно этот механизм не может быть использован ни для чего, кроме как для сравнения моделей.

Генеративно-состязательная перспектива является самой современной точкой зрения на данный вопрос (Ian Goodfellow et al., 2014). По сути, эта перспектива утверждает, что «лучшая» вероятностная модель — та, на основе которой можно генерировать результаты методом Монте-Карло, неотличимые от реальных результатов. Например, если рассмотреть исторический список транзакций в местном гипермаркете, можно обрезать эту историю в произвольный момент в прошлом и с помощью вероятностной модели генерировать фальшивые, но реалистичные транзакции впоследствии. Модель будет считаться «идеальной», если окажется невозможным посредством статистического анализа определить момент перехода набора данных от «реальных» к «фальшивым» данным. Суть генеративно-состязательного подхода заключается в том, чтобы «изучить» метрики, выявляющие недостатки любой вероятностной модели. Вместо того чтобы фокусироваться на конкретной метрике, эта перспектива рекурсивно использует методы машинного обучения для «изучения» самих метрик.

Поиск лучших способов оценки качества вероятностных прогнозов остаётся активной областью исследований. Нет чёткого разграничения между вопросами «Как создать лучший прогноз?» и «Как определить, что прогноз лучше?». Недавние исследования значительно размыли границы между этими направлениями, и, вероятно, следующие прорывы будут связаны с дальнейшими изменениями в подходе к вероятностным прогнозам.

Практически нулевые вероятности и логарифмическое правдоподобие

Очень маленькие вероятности естественным образом возникают при рассмотрении многомерной ситуации через призму вероятностных прогнозов. Эти маленькие вероятности являются проблематичными, поскольку компьютеры не обрабатывают числа с неограниченной точностью. Сырые значения вероятностей часто оказываются «практически нулевыми» в том смысле, что они округляются до нуля из-за ограничений числовой точности. Решение этой проблемы заключается не в смене программного обеспечения на вычисления с произвольной точностью — что крайне неэффективно с точки зрения вычислительных ресурсов —, а в использовании «логарифмического трюка», который превращает умножения в сложения. Этот трюк используется — так или иначе — практически каждым программным обеспечением, работающим с вероятностными прогнозами.

Предположим, что у нас есть случайные величины $$X_1, X_2, \ldots, X_n$$, представляющие спрос за день для всех $$n$$ различных товаров, предлагаемых в данном магазине. Пусть $$\hat{x}_1, \hat{x}_2, \ldots, \hat{x}_n$$ соответствуют эмпирически зафиксированному спросу в конце дня для каждого товара. Для первого товара — описываемого через $$X_1$$ — вероятность наблюдения $$\hat{x}_1$$ записывается как $$P(X_1=\hat{x}_1)$$. Теперь предположим, несколько упрощённо, но для ясности, что все товары являются строго независимыми с точки зрения спроса. Вероятность совместного события наблюдения $$\hat{x}_1, \hat{x}_2, \ldots, \hat{x}_n$$ равна:

Если $$P(X_k=\hat{x}_k) \approx \tfrac{1}{2}$$ (грубое приближение) и $$n=10000$$, то совместная вероятность выше имеет порядок $$\tfrac{1}{{2^{10000}}} \approx 5 \times 10^{-3011}$$, что является очень маленьким значением. Это значение выходит за пределы представимых чисел, даже с учётом 64-битных чисел с плавающей точкой, которые обычно используются в научных вычислениях.

«Логарифмический трюк» заключается в работе с логарифмом данного выражения, то есть:

Логарифм превращает серию умножений в серию сложений, что оказывается гораздо более устойчивым с числовой точки зрения, чем серия умножений.

Использование «логарифмического трюка» часто необходимо при работе с вероятностными прогнозами. Логарифмическое правдоподобие — это буквально логарифм правдоподобия (введённого ранее), именно потому, что сырое правдоподобие обычно было бы численно не представимо с учётом распространённых типов чисел с плавающей точкой.

Алгоритмические особенности вероятностных прогнозов

Вопрос о компьютерной генерации вероятностных прогнозов почти так же обширен, как и область машинного обучения. Разграничения между этими двумя направлениями, если таковые существуют, в основном являются вопросом субъективного выбора. Тем не менее, в этом разделе представлен довольно выборочный список заметных алгоритмических подходов, которые можно использовать для получения вероятностных прогнозов.

В начале XX века, возможно, в конце XIX века, появилась идея расчёта страхового запаса, при которой неопределённость спроса моделируется с помощью нормального распределения. Поскольку таблицы нормального распределения уже были созданы для других наук, в частности для физики, применение страхового запаса требовало лишь умножения уровня спроса на коэффициент «страхового запаса», взятый из готовой таблицы. По рассказам, многие учебники по цепям поставок, написанные до 1990-х годов, до сих пор содержали таблицы нормального распределения в приложениях. К сожалению, основной недостаток этого подхода заключается в том, что нормальные распределения не являются разумным предположением для цепочек поставок. Во-первых, с точки зрения цепочек поставок можно с уверенностью сказать, что ничто никогда не распределено нормально. Во-вторых, нормальное распределение является непрерывным, что противоречит дискретной природе событий цепочки поставок (см. «Закон малых чисел» выше). Таким образом, хотя по сути «страховые запасы» имеют вероятностную составляющую, основная методология и вычислительные приёмы решительно ориентированы на детерминированный подход. Этот подход приведён здесь, однако, для ясности.

Перенесемся в начало 2000-х, когда методы ансамблевого обучения — наиболее известными представителями которых, вероятно, являются случайные леса и градиентный бустинг деревьев — относительно легко расширялись от своих детерминированных основ до вероятностной перспективы. Ключевая идея ансамблевого обучения заключается в комбинировании многочисленных слабых детерминированных предсказателей, таких как решающие деревья, для создания превосходящего детерминированного предсказателя. Однако можно скорректировать процесс смешивания для получения вероятностей, а не просто единой совокупной величины, таким образом превращая метод ансамблевого обучения в вероятностный метод прогнозирования. Эти методы являются непараметрическими и способны аппроксимировать распределения с толстыми хвостами и/или мультимодальные распределения, как это обычно наблюдается в цепочке поставок. У этих методов, как правило, есть два заметных недостатка. Во-первых, по своей конструкции функция плотности вероятности, создаваемая этим классом моделей, содержит множество нулей, что препятствует попыткам использовать метрику логарифмического правдоподобия. Более того, эти модели не совсем соответствуют байесовской перспективе, поскольку новые наблюдения часто модель считает «невозможными» (то есть с нулевой вероятностью). Однако эту проблему можно решить с помощью методов регуляризации¹. Во-вторых, модели, как правило, настолько велики, как значительная часть исходного набора данных, а операция «предсказания» оказывается почти столь же вычислительно затратной, как и операция «обучения».

Гиперпараметрические методы, объединяемые под названием «глубокое обучение», которое взорвалось в 2010-х, были, почти случайно, вероятностными. Действительно, хотя подавляющее большинство задач, в которых глубокое обучение действительно блистает (например, классификация изображений), фокусируется исключительно на детерминированных прогнозах, оказывается, что метрика кросс-энтропии — вариант логарифмического правдоподобия, обсуждавшегося выше — обладает очень крутыми градиентами, которые часто хорошо подходят для стохастического градиентного спуска (SGD), лежащего в основе методов глубокого обучения. Таким образом, модели глубокого обучения строятся как вероятностные не потому, что вероятности представляли интерес, а потому, что градиентный спуск сходится быстрее, когда функция потерь отражает вероятностный прогноз. Таким образом, в отношении глубокого обучения цепочка поставок отличается своим интересом к реальному вероятностному выводу модели глубокого обучения, в то время как большинство других случаев использования сводят распределение вероятностей к его среднему, медиане или моде. Смешанные плотностные сети — это тип сети глубокого обучения, направленной на изучение сложных распределений вероятностей. Сам результат представляет собой параметрическое распределение, возможно, состоящее из гауссовских компонент. Однако, в отличие от «страховых запасов», смесь многих гауссов может на практике отражать поведение с толстыми хвостами, наблюдаемое в цепочках поставок. Хотя методы глубокого обучения часто считаются передовыми, следует отметить, что достижение численной стабильности, особенно когда речь идет о плотностных смесях, остается несколько «темным искусством».

Дифференцируемое программирование является продолжением глубокого обучения, которое получило популярность в самом конце 2010-х. Оно разделяет многие технические характеристики глубокого обучения, но значительно отличается по фокусу. В то время как глубокое обучение направлено на обучение произвольных сложных функций (например, игра в го) путем объединения большого количества простых функций (например, свёрточных слоев), дифференцируемое программирование сосредоточено на тонкой структуре процесса обучения. Самая детализированная, самая выразительная структура, буквально, может быть оформлена в виде программы, которая включает условные операторы, циклы, вызовы функций и т.д. Дифференцируемое программирование представляет особый интерес для цепочки поставок, поскольку задачи, как правило, имеют высокую структурированность, и эти структуры известны экспертам². Например, продажи одной конкретной рубашки могут снижаться из-за продаж другой рубашки другого цвета, но не будут снижаться из-за продаж рубашки, отличающейся на три размера. Такие структурные предпосылки являются ключевыми для достижения высокой эффективности использования данных. Действительно, с точки зрения цепочки поставок объем данных, как правило, очень ограничен (см. закон малых чисел). Поэтому структурирование проблемы помогает обеспечить изучение необходимых статистических закономерностей даже при ограниченном объеме данных. Структурные предпосылки также помогают решать задачи численной стабильности. По сравнению с ансамблевыми методами, структурирование проблемы занимает меньше времени, чем инженерия признаков; обслуживание модели также упрощается. С другой стороны, дифференцируемое программирование остается довольно молодой перспективой на сегодняшний день.

Подход методом Монте-Карло (1930/1940) можно использовать для рассмотрения вероятностных прогнозов с другой стороны. До сих пор обсуждаемые модели предоставляют явные функции плотности вероятности (PDF). Однако с точки зрения метода Монте-Карло модель можно заменить генератором — или сэмплером — который случайным образом генерирует возможные исходы (иногда называемые «отклонениями»). Функции плотности вероятности можно восстановить путем усреднения результатов работы генератора, хотя зачастую функции плотности обходят стороной, чтобы снизить требования к вычислительным ресурсам. Действительно, генератор часто проектируется так, чтобы быть значительно более компактным — с точки зрения данных — чем представляемые им функции плотности. Большинство методов машинного обучения — включая перечисленные выше, предназначенные для непосредственного решения задач вероятностного прогнозирования — могут способствовать обучению генератора. Генераторы могут принимать форму низкоразмерных параметрических моделей (например, моделей состояния) или гиперпараметрических моделей (например, моделей LSTM и GRU в глубоких нейронных сетях). Ансамблевые методы редко используются для поддержки генеративных процессов из-за их высоких вычислительных затрат на операцию «предсказания», которая широко применяется в подходе Монте-Карло.

Работа с вероятностными прогнозами

Получение полезных инсайтов и принятие решений на основе вероятностных прогнозов требует специализированных численных инструментов. В отличие от детерминированных прогнозов, где используются просто числа, сами прогнозы представлены либо явными функциями плотности вероятности, либо генераторами Монте-Карло. Качество работы вероятностных инструментов на практике столь же важно, как и качество самих вероятностных прогнозов. Без этих инструментов использование вероятностных прогнозов сводится к детерминированному процессу (подробнее об этом в разделе «Антипаттерны» ниже).

Например, инструменты должны уметь выполнять следующие задачи:

• Объединить неопределенное время производства с неопределенным временем транспортировки, чтобы получить «общее» неопределенное время выполнения заказа.
• Объединить неопределенный спрос с неопределенным временем выполнения заказа, чтобы получить «общий» неопределенный спрос, который должен быть покрыт запасами.
• Объединить неопределенные возвраты заказов (электронная коммерция) с неопределенной датой прибытия заказа поставщика в транзите, чтобы получить неопределенное время выполнения заказа для клиента.
• Расширить прогноз спроса, полученный статистическим методом, добавив риск хвоста, определенный вручную на основе понимания контекста, не отраженного в исторических данных, например, пандемии.
• Объединить неопределенный спрос с неопределенным состоянием запасов с учетом срока годности (розничная торговля продуктами), чтобы получить неопределенное количество оставшихся запасов к концу дня.
• …

Как только все вероятностные прогнозы — и не только по спросу — будут корректно объединены, следует осуществить оптимизацию решений в цепочке поставок. Это включает вероятностный анализ ограничений, а также функцию оценки. Однако аспект инструментов выходит за рамки настоящего документа.

Существует два основных «подхода» к инструментам для работы с вероятностными прогнозами: во-первых, алгебры над случайными величинами, во-вторых, вероятностное программирование. Эти два подхода дополняют друг друга, поскольку у них разный набор преимуществ и недостатков.

Алгебра случайных величин обычно работает с явными функциями плотности вероятности. Она поддерживает обычные арифметические операции (сложение, вычитание, умножение и т.д.), но перенесенные в вероятностную область, часто при этом предполагая статистическую независимость случайных величин. Такая алгебра обеспечивает численную стабильность, почти на уровне её детерминированного аналога (то есть простых чисел). Все промежуточные результаты могут быть сохранены для последующего использования, что оказывается весьма полезным для организации и устранения неполадок в конвейере извлечения данных. С другой стороны, выразительность этих алгебр, как правило, ограничена, поскольку обычно невозможно выразить все тонкие условные зависимости, существующие между случайными величинами.

Вероятностное программирование принимает метод Монте-Карло для решения задачи. Логика записывается один раз, обычно с полностью детерминированной точки зрения, но выполняется многократно с помощью инструментов (то есть процесса Монте-Карло) для сбора необходимых статистических данных. Максимальная выразительность достигается за счет «программных» конструкций: можно смоделировать произвольные, сложные зависимости между случайными величинами. Запись логики посредством вероятностного программирования также, как правило, оказывается несколько проще по сравнению с алгеброй случайных величин, поскольку логика включает лишь обычные числа. С другой стороны, существует постоянный компромисс между численной стабильностью (большее число итераций обеспечивает лучшую точность) и вычислительными ресурсами (большее число итераций требует больше ресурсов). Кроме того, промежуточные результаты, как правило, не сохраняются, поскольку их существование носит лишь временный характер — именно для того, чтобы снизить нагрузку на вычислительные ресурсы..

Недавние исследования в области глубокого обучения также указывают на то, что существуют и другие подходы, помимо двух описанных выше. Например, вариационные автокодировщики предлагают перспективы для выполнения операций над латентными пространствами, дающих впечатляющие результаты при реализации очень сложных преобразований данных (например: автоматическое удаление очков с портрета на фотографии). Хотя эти подходы концептуально весьма интригующи, на сегодняшний день они не показали значительной практической ценности при решении проблем цепочки поставок.

Визуализация вероятностных прогнозов

Самый простой способ визуализировать дискретное распределение вероятностей — это гистограмма, где вертикальная ось указывает вероятность, а горизонтальная ось — значение интересующей случайной величины. Например, вероятностный прогноз времени выполнения заказа можно отобразить следующим образом:

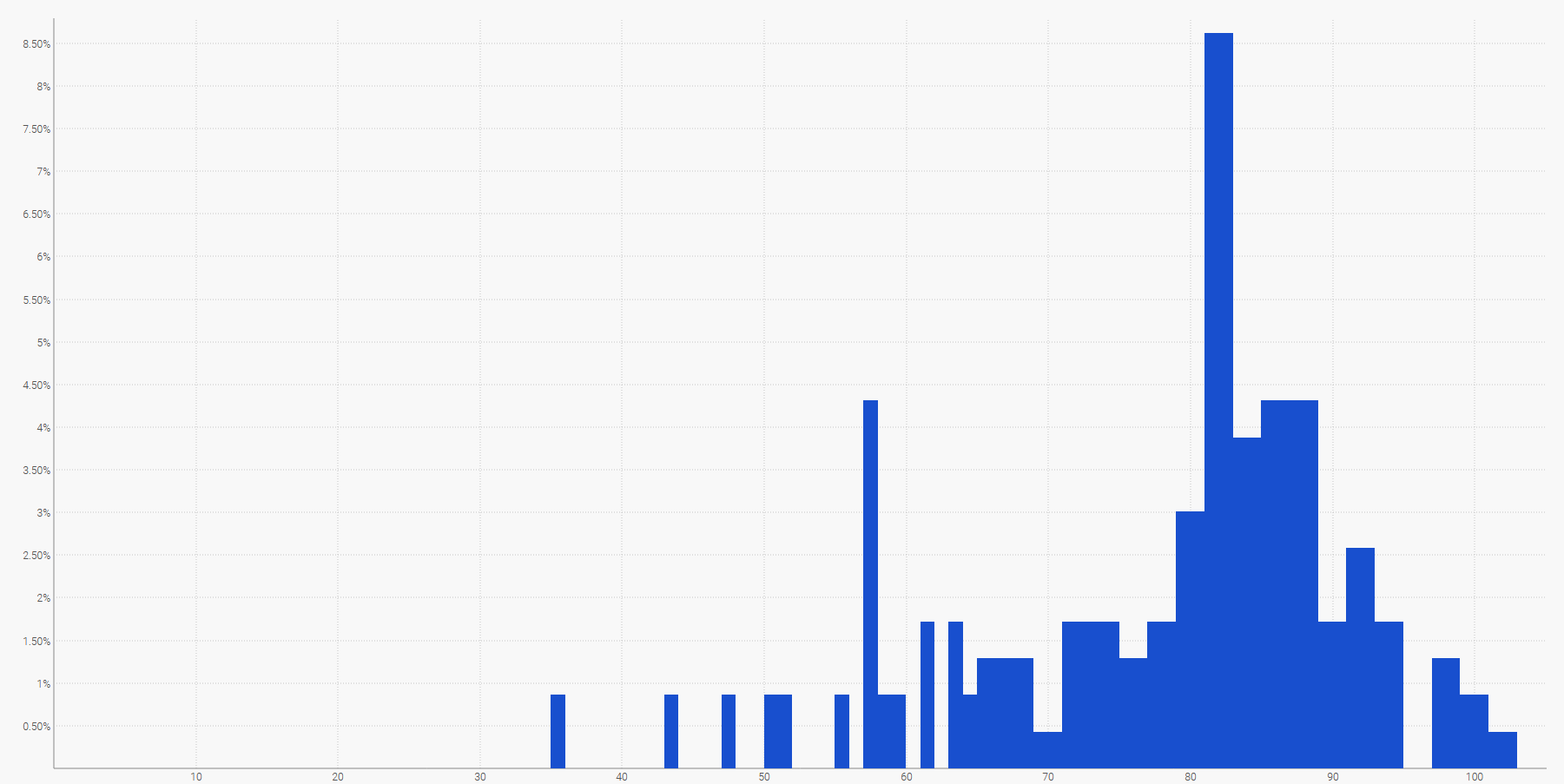
Будущий спрос, суммированный за определенный период времени, также может быть представлен в виде гистограммы. Более того, гистограмма подходит для всех одномерных случайных величин, принадлежащих $${ℤ}$$, множеству целых чисел.

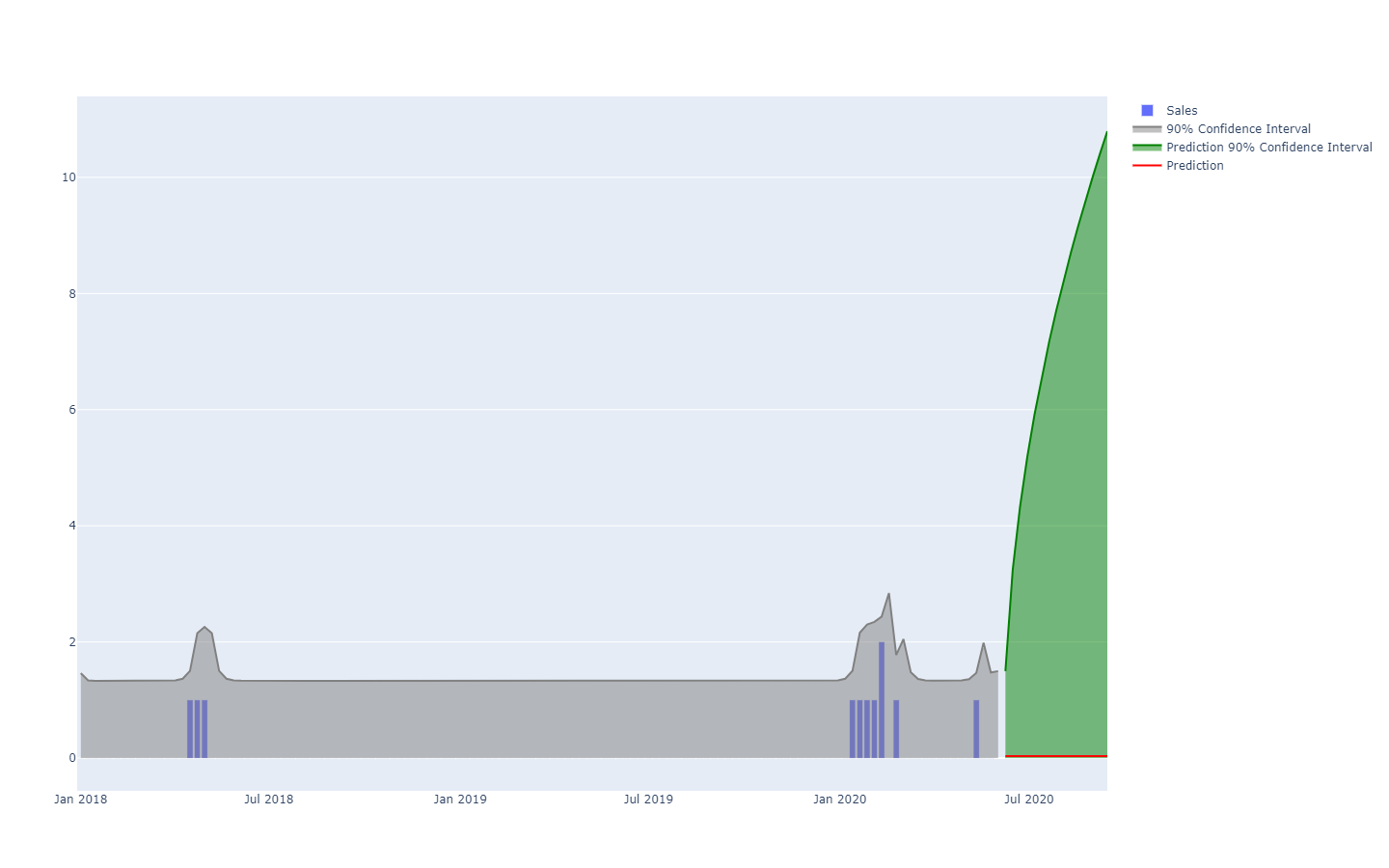
Визуализация вероятностного аналога равномерно распределенного временного ряда — т.е. величины, изменяющейся по дискретным равным промежуткам времени — уже гораздо сложнее. Действительно, в отличие от одномерной случайной величины, для такого распределения нет канонической визуализации. Учтите, что промежутки нельзя считать взаимно независимыми. Таким образом, хотя возможно представить «вероятностный» временной ряд как серию гистограмм — по одной на каждый период — такое представление существенно искажает характер развития событий в цепочке поставок.

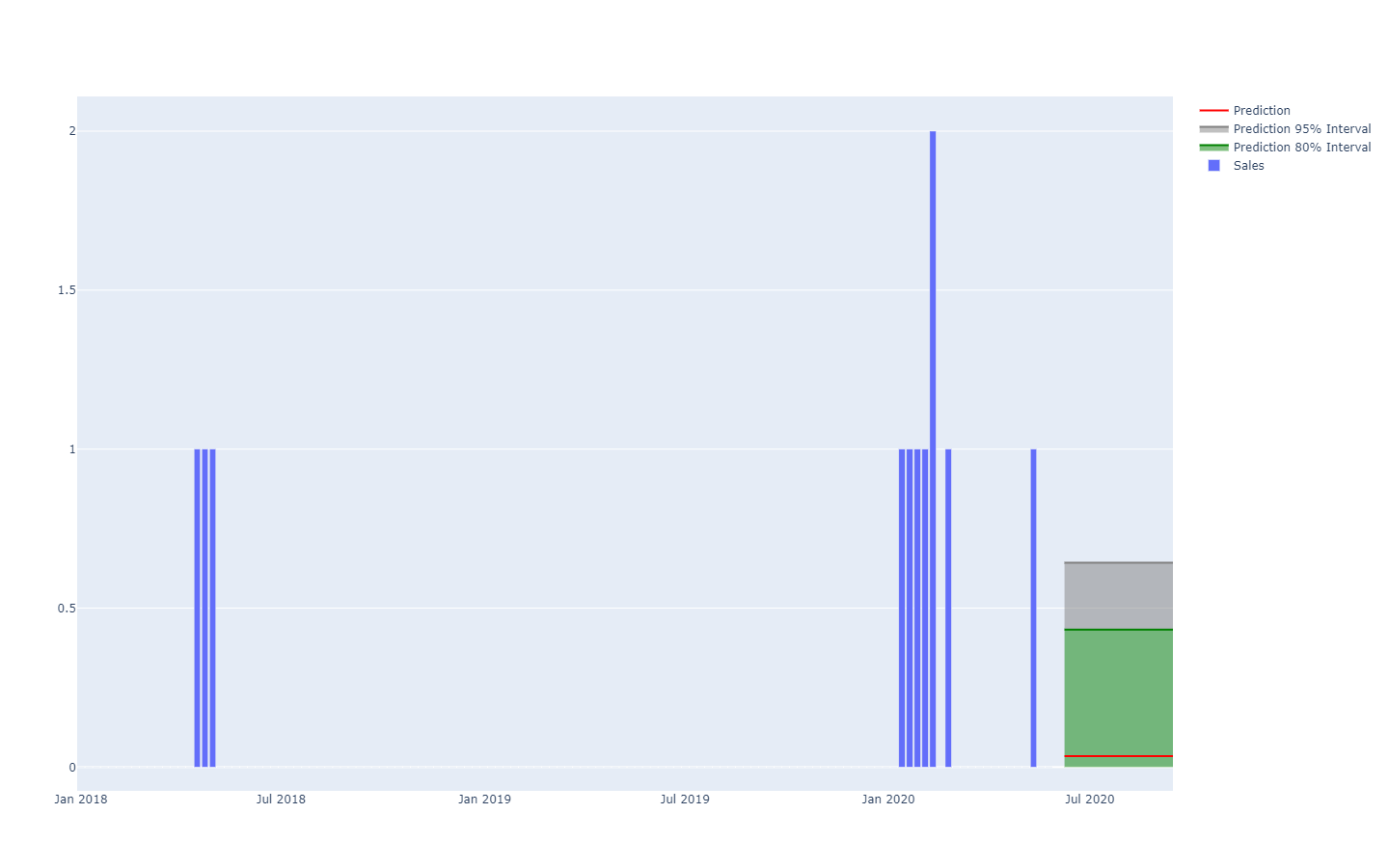
Например, не исключено, что новый продукт покажет хорошие результаты и достигнет высоких объемов продаж (успех). Также не исключено, что тот же новый продукт потерпит неудачу и покажет низкие объемы продаж (провал). Однако огромные колебания от дня к дню между успешными и неудачными продажами крайне маловероятны.

Доверительные интервалы, как это обычно описывается в литературе по цепочкам поставок, несколько вводят в заблуждение. Они, как правило, подчеркивают ситуации с низкой неопределенностью, которые не характерны для реальных условий цепочки поставок;

Обратите внимание, что эти доверительные интервалы представляют собой именно распределения вероятностей, размещенные рядом друг с другом с цветовыми схемами, подчеркивающими определенные квантильные пороги.

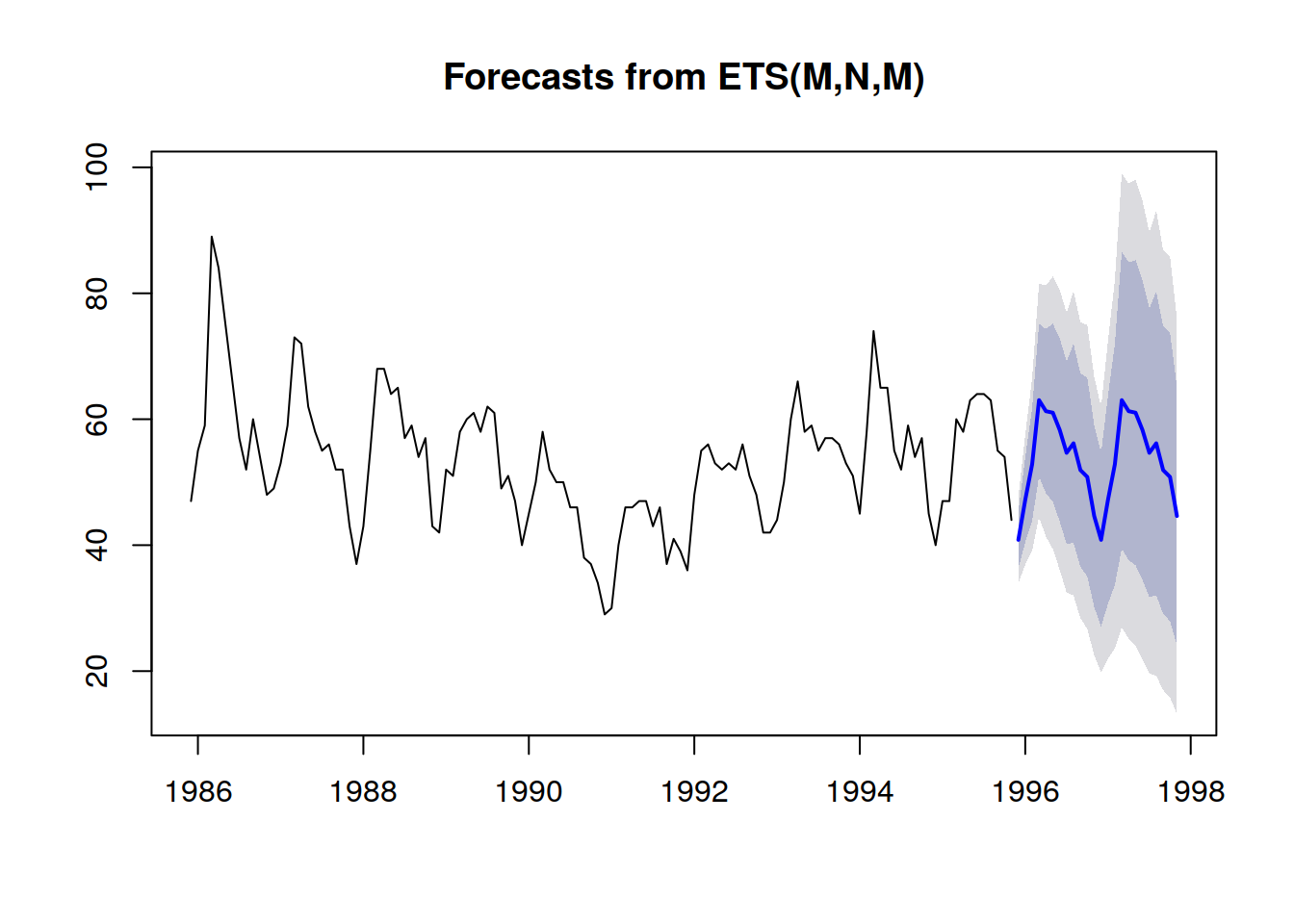
Лучшим представлением — то есть, которое не игнорирует сильные зависимости между периодами — является рассмотрение кумулятивных значений во времени, вычисление их квантилей, а затем дифференцирование для восстановления приростов за каждый период (см. первую иллюстрацию вероятностного прогноза в начале данной статьи). Визуализация остается той же, но лежащая в ее основе семантика отличается. Теперь мы анализируем квантильные значения сценариев, выделяя чрезвычайно благоприятные (соответственно, неблагоприятные) сценарии.

Антипаттерны вероятностного прогнозирования

Вероятностные прогнозы бросают вызов тому, как многие интуитивно воспринимают будущее. В этом разделе мы рассмотрим некоторые из наиболее часто неправильно понимаемых аспектов вероятностного прогнозирования.

Не существует «непредсказуемых» событий

С точки зрения детерминированного подхода предсказать результат лотереи невозможно, поскольку шанс угадать составляет «один к миллиону». Однако с вероятностной точки зрения задача тривиальна: каждый билет имеет шанс «один к миллиону» на победу. Очень высокая дисперсия результата не должна отождествляться с какой-либо «неизученностью» явления, которое можно вполне понять, как в случае с лотереей. Вероятностное прогнозирование заключается в количественной оценке и структурировании дисперсии, а не в устранении самой дисперсии.

Не существует «нормальных» распределений

Нормальные распределения, также известные как гауссовы, встречаются повсеместно как в учебниках по цепочке поставок, так и по физике. Однако, когда дело касается человеческих дел, почти ничего не распределено «нормально». Нормальные распределения по своей природе делают крупные отклонения (по сравнению со средними отклонениями) чрезвычайно редкими, до такой степени, что модель исключает их как практически невозможные – то есть вероятность меньше, чем один к миллиарду. Спрос, время выполнения заказа, возвраты – это многие закономерности, которые категорически не распределяются нормально. Единственное преимущество нормальных распределений заключается в том, что они хорошо подходят для создания учебных задач для студентов, поскольку позволяют получать явные аналитические решения.

Избирательный выбор вероятностей

При столкновении с распределением вероятностей возникает соблазн выбрать одну точку распределения, возможно, среднее или медиану, и действовать на основании этого значения. Этот процесс противоречит самой сути вероятностного аспекта прогноза. Вероятности не следует сводить к единой точечной оценке, поскольку независимо от того, какая точка выбрана, этот процесс приводит к огромной потере информации. Таким образом, несмотря на то, что это может показаться несколько тревожным, предполагается сохранять вероятности в исходном виде как можно дольше. Точка свёртывания обычно наступает при финальном решении в цепочке поставок, которое максимизирует доходы в условиях неопределённого будущего.

Удаление статистических выбросов

Большинство классических численных методов – твёрдо основанных на детерминистском подходе к прогнозированию (например, скользящие средние) – ведут себя крайне плохо при встрече со статистическими выбросами. Поэтому многие компании устанавливают процессы для ручного «очищения» исторических данных от этих выбросов. Однако необходимость такого процесса очистки лишь подчеркивает недостатки этих численных методов. Напротив, статистические выбросы являются важным компонентом вероятностного прогноза, поскольку они способствуют лучшему пониманию происходящего в хвосте распределения. Другими словами, эти выбросы являются ключом к количественной оценке вероятности появления новых выбросов.

Принести меч на перестрелку

Для работы с распределениями вероятностей требуются специализированные инструменты. Создание вероятностного прогноза – это лишь один из многих шагов, необходимых для предоставления реальной ценности компании. Многие специалисты по цепочке поставок в итоге отвергают вероятностные прогнозы из-за отсутствия подходящих инструментов для работы с ними. Многие корпоративные поставщики программного обеспечения присоединились к этой тенденции и теперь заявляют о поддержке «вероятностного прогнозирования» (наряду с «AI» и «blockchain»), но никогда не заходят дальше косметической реализации нескольких вероятностных моделей (см. раздел выше). Демонстрация модели вероятностного прогнозирования практически ничего не стоит без обширных инструментов для использования её числовых результатов.

Заметки