Обобщение (Прогнозирование)
Обобщение — это способность алгоритма генерировать модель, используя набор данных, которая хорошо работает на ранее невидимых данных. Обобщение имеет критическое значение для цепочки поставок, поскольку большинство решений основано на предвосхищении будущего. В контексте прогнозирования данные являются невидимыми, потому что модель предсказывает будущие события, которые нельзя наблюдать. Хотя с 1990-х годов достигнут значительный прогресс как в теоретическом, так и в практическом плане по проблеме обобщения, истинное обобщение до сих пор остаётся неуловимым. Полное разрешение проблемы обобщения может оказаться не сильно отличным от разрешения проблемы искусственного общего интеллекта. Более того, цепочка поставок добавляет множество своих запутанных проблем поверх основных сложностей обобщения.
Обзор парадокса
Создание модели, которая идеально работает на имеющихся данных, является простой задачей: достаточно полностью запомнить набор данных, а затем использовать сам набор данных для ответа на любой запрос о нём. Поскольку компьютеры хорошо умеют записывать большие наборы данных, разработка такой модели проста. Однако это обычно оказывается бессмысленным1, поскольку смысл наличия модели заключается в её способности предсказывать за пределами уже наблюденного.
Кажется, неизбежный парадокс заключается в следующем: хорошая модель — это та, которая хорошо работает на данных, которые в данный момент недоступны, но, по определению, если данные недоступны, то оценить её невозможно. Таким образом, термин «обобщение» относится к неуловимой способности некоторых моделей сохранять свою актуальность и качество за пределами наблюдений, доступных на момент создания модели.
Хотя запоминание наблюдений можно расценить как неадекватную стратегию моделирования, любая альтернативная стратегия создания модели потенциально подвержена той же проблеме. Независимо от того, как хорошо модель, похоже, работает на текущих доступных данных, всегда можно предположить, что это всего лишь случайность, или, что ещё хуже, дефект стратегии моделирования. То, что поначалу может показаться пограничным статистическим парадоксом, на самом деле является широко распространённой проблемой.
В качестве примерного свидетельства, в 1979 году Комиссия по ценным бумагам и биржам (SEC), американское агентство, ответственное за регулирование рынков капитала, ввело своё знаменитое Правило 156. Это правило требует от управляющих фондами информировать инвесторов о том, что прошлая производительность не является показателем будущих результатов. Прошлая производительность подразумевается как «модель», которой SEC предостерегает не доверять в отношении её способности к «обобщению», то есть её возможности что-либо предсказать о будущем.
Даже наука сама испытывает трудности с тем, что означает экстраполяция «истины» за пределы узкого круга наблюдений. Скандалы, связанные с «плохой наукой», разворачивавшиеся в 2000-х и 2010-х годах вокруг p-hacking, показывают, что целые области исследований вышли из строя и им нельзя доверять2. Хотя существуют случаи откровенного мошенничества, когда экспериментальные данные были явно подделаны, чаще всего суть проблемы кроется в моделях; то есть в интеллектуальном процессе, используемом для обобщения наблюдаемого.
В своей наиболее всеобъемлющей форме проблема обобщения неотличима от самой науки, а значит, она так же сложна, как и воспроизведение всей широты человеческой изобретательности и потенциала. Однако более узкое статистическое видение проблемы обобщения значительно проще для понимания, и именно эта перспектива будет использоваться в последующих разделах.
Появление новой науки
Обобщение возникло как статистическая парадигма на рубеже 20-го века, преимущественно через призму точности прогнозирования3, что представляет собой частный случай, тесно связанный с прогнозами для временных рядов. В начале 1900-х годов появление среднего класса, владеющего акциями, в США вызвало огромный интерес к методам, которые помогли бы людям обеспечить финансовую отдачу от их торговых активов. Как гадалки, так и экономические прогнозисты снисходительно пытались экстраполировать будущие события для публики, охотно за это платившей. Были как сделаны, так и потеряны состояния, но эти усилия почти не прояснили «правильного» подхода к решению проблемы.
В основном обобщение оставалось загадочной проблемой на протяжении большей части 20-го века. Даже не было ясно, принадлежит ли она к области естественных наук, управляемых наблюдениями и экспериментами, или к области философии и математики, управляемых логикой и внутренней согласованностью.
Ситуация продолжалась до судьбоносного момента в 1982 году, года первого публичного соревнования по прогнозированию — разговорно известного как соревнование M4. Принцип был прост: опубликовать набор данных из 1000 усечённых временных рядов, позволить участникам представить свои прогнозы, а затем опубликовать оставшуюся часть набора данных (усечённые хвосты) вместе с достигнутыми участниками точностями. Благодаря этому соревнованию обобщение, всё ещё рассматриваемое через призму точности прогнозирования, вошло в область естественных наук. В дальнейшем соревнования по прогнозированию стали проводиться всё чаще.
Несколько десятилетий спустя, в 2010 году, Kaggle добавил новое измерение в такие соревнования, создав платформу, посвящённую общим задачам прогнозирования (а не только временным рядам). По состоянию на февраль 2023 года5 платформа организовала 349 соревнования с денежными призами. Принцип остаётся тем же, что и у оригинального соревнования M: предоставляется усечённый набор данных, участники представляют свои ответы на заданные задачи прогнозирования, а затем публикуются рейтинги вместе с скрытой частью набора данных. Эти соревнования всё ещё считаются золотым стандартом для правильной оценки ошибки обобщения моделей.
Переобучение и недообучение
Переобучение, как и его антонимичное недообучение, является проблемой, которая часто возникает при создании модели на основе заданного набора данных, и подрывает способность модели к обобщению. Исторически6 переобучение зарекомендовало себя как первая хорошо понятная преграда на пути к обобщению.
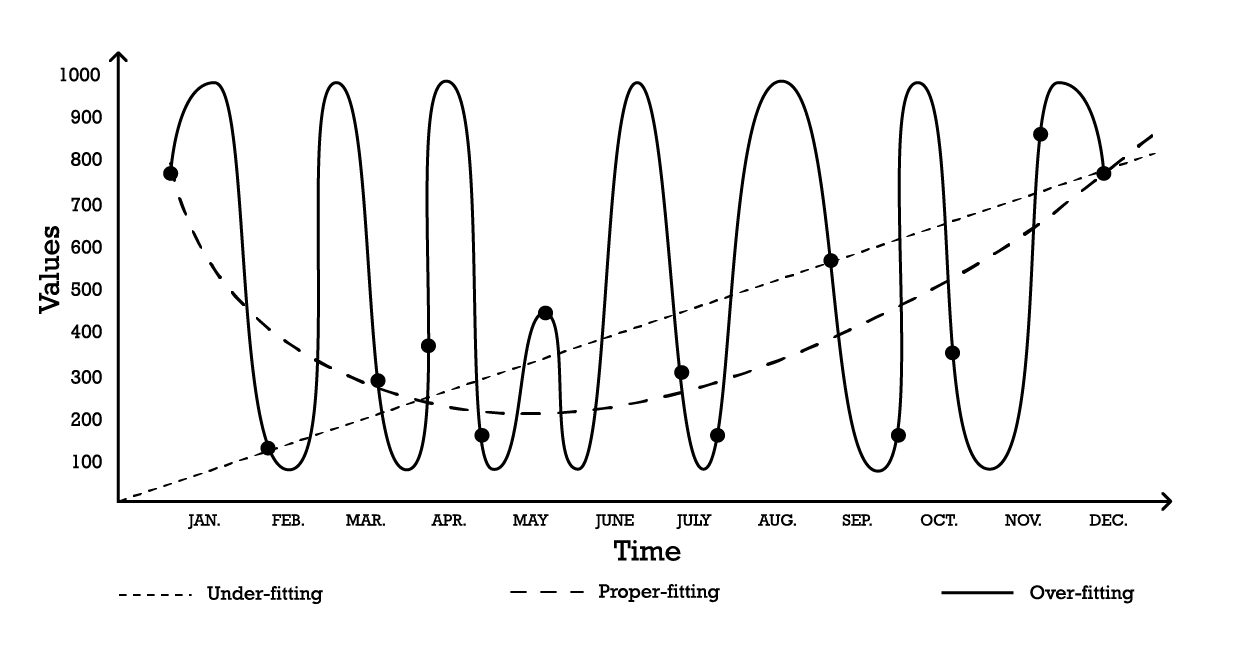
Визуализировать переобучение можно с помощью простой задачи моделирования временных рядов. Для целей этого примера предположим, что цель заключается в создании модели, которая отражает серию исторических наблюдений. Одним из самых простых вариантов моделирования этих наблюдений является линейная модель, как показано ниже (см. Рисунок 1).

Рисунок 1: Составной график, иллюстрирующий три различных попытки «подгона» серии наблюдений.
С двумя параметрами модель «недообучения» является устойчивой, но, как подсказывает название, она недообучает данные, поскольку явно не способна уловить общую форму распределения наблюдений. Этот линейный подход имеет высокое смещение, но низкую дисперсию. В этом контексте смещение следует понимать как присущее ограничение стратегии моделирования в умении уловить тонкости наблюдений, а дисперсию — как чувствительность к малым колебаниям, возможно, шуму, в наблюдениях.
Можно принять довольно сложную модель, как показано на кривой «переобучения» (Рисунок 1). Эта модель включает в себя множество параметров и точно подгоняет наблюдения. Такой подход имеет низкое смещение, но явно высокую дисперсию. В качестве альтернативы можно выбрать модель промежуточной сложности, как видно на кривой «правильного подгона» (Рисунок 1). Эта модель включает три параметра, имеет среднее смещение и среднюю дисперсию. Из этих трёх вариантов именно модель с правильным подбором всегда оказывается наилучшей с точки зрения обобщения.
Эти варианты моделирования отражают суть компромисса между смещением и дисперсией.7 8 Компромисс между смещением и дисперсией — это общий принцип, который гласит, что смещение можно уменьшить за счёт увеличения дисперсии. Ошибка обобщения минимизируется при нахождении правильного баланса между уровнем смещения и дисперсии.
Исторически, с начала 20-го века до начала 2010-х годов переобученную модель определяли9 как модель, содержащую больше параметров, чем это оправдано данными. Действительно, на первый взгляд, добавление слишком большого количества степеней свободы в модель кажется идеальным рецептом для проблем переобучения. Однако появление глубокого обучения доказало, что эта интуиция и определение переобучения вводят в заблуждение. Этот момент будет рассмотрен повторно в разделе о глубоком двойном спуске.
Кросс-валидация и ретроспективное тестирование
Кросс-валидация — это метод валидации модели, используемый для оценки того, насколько хорошо модель будет обобщаться за пределами исходного набора данных. Это метод подвыборки, который использует различные части данных для поочередного тестирования и обучения модели на разных итерациях. Кросс-валидация является основой современных практик прогнозирования, и практически все победители соревнований по прогнозированию широко используют кросс-валидацию.
Существует множество вариантов кросс-валидации. Наиболее популярным является k-кратная валидация, при которой исходная выборка случайным образом разбивается на k подвыборок. Каждая подвыборка используется один раз в качестве валидационных данных, в то время как остальные — все остальные подвыборки — используются в качестве тренировочных данных.
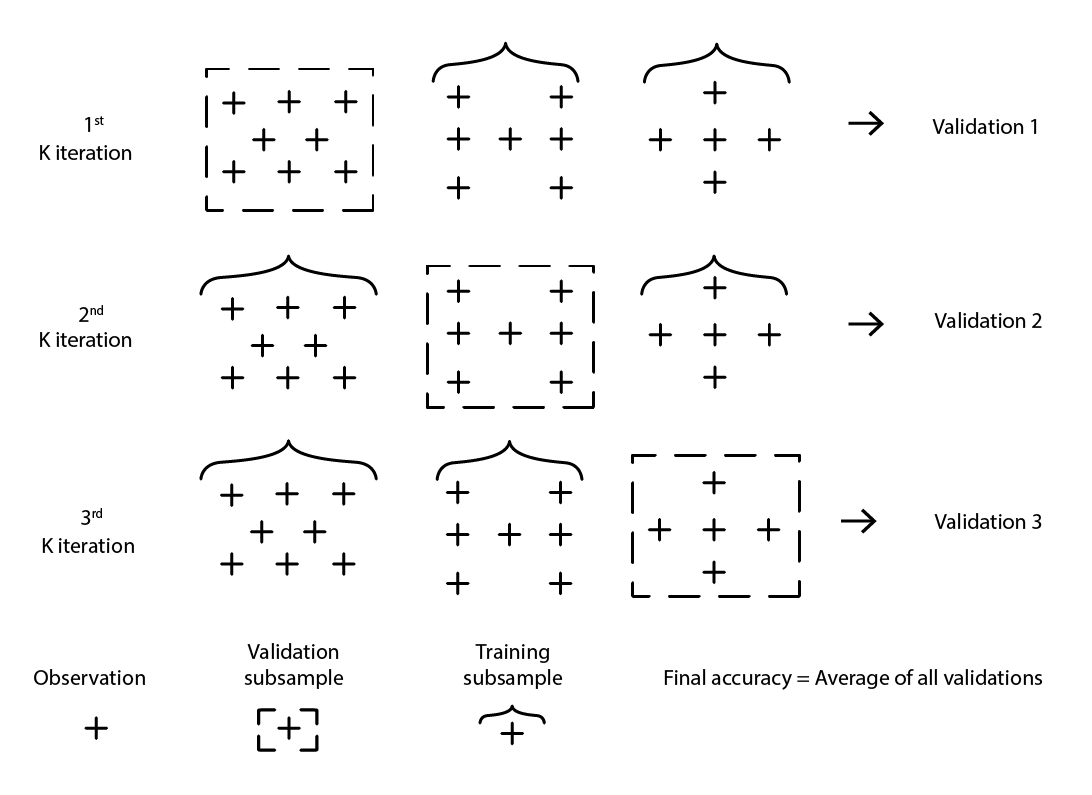
Рисунок 2: Пример k-кратной валидации. Все приведённые наблюдения взяты из одного и того же набора данных. Эта техника таким образом создает подвыборки данных для целей валидации и обучения.
Выбор значения k, количества подвыборок, представляет собой компромисс между маржинальным статистическим приростом и требованиями к вычислительным ресурсам. Действительно, при k-кратной валидации вычислительные ресурсы растут линейно с увеличением k, в то время как преимущества в снижении ошибки резко уменьшаются10. На практике выбор значения 10 или 20 для k обычно является «достаточно хорошим», так как статистический прирост при больших значениях не оправдывает дополнительные неудобства, связанные с увеличенными затратами вычислительных ресурсов.
Кросс-валидация предполагает, что набор данных можно разложить на серию независимых наблюдений. Однако в цепочке поставок это часто не так, поскольку набор данных обычно отражает некий исторический контекст, где присутствует зависимость от времени. При наличии временного компонента тренировочная подвыборка должна строго «предшествовать» валидационной. Иными словами, «будущее» относительно контрольной точки ресэмплинга не должно проникать в валидационную подвыборку.
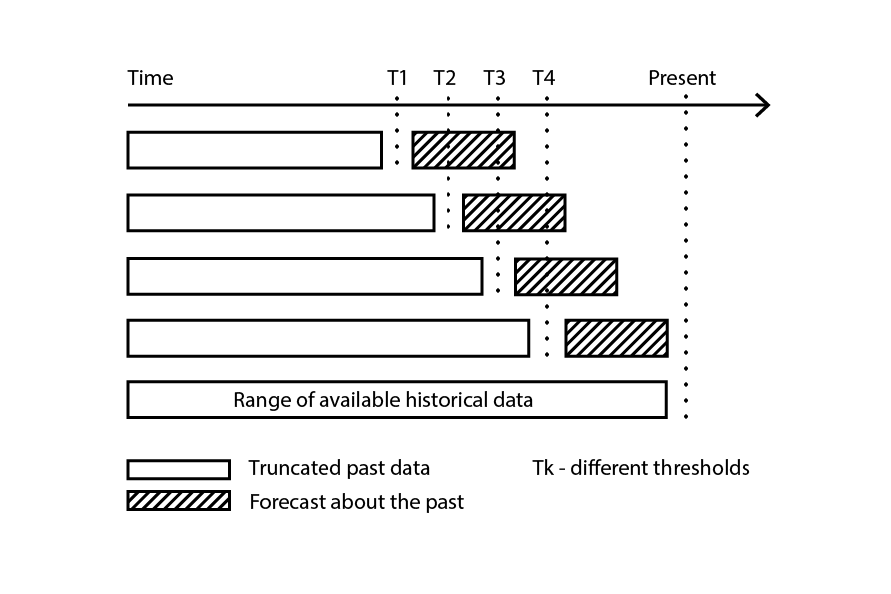
Рисунок 3: Пример процесса ретроспективного тестирования, создающего подвыборки данных для валидации и обучения.
Ретроспективное тестирование представляет собой разновидность кросс-валидации, которая напрямую учитывает зависимость от времени. Вместо случайных подвыборок для тренировочных и валидационных данных используется контрольная точка: наблюдения до контрольной точки относятся к тренировочным данным, а наблюдения после — к валидационным. Процесс повторяется с выбором ряда различных контрольных точек.
Метод ресэмплинга, лежащий в основе как кросс-валидации, так и ретроспективного тестирования, является мощным механизмом, направляющим процесс моделирования в сторону лучшей обобщаемости. Фактически, он настолько эффективен, что существует целый класс алгоритмов (машинного) обучения, в которых этот механизм занимает центральное место. Наиболее заметными из них являются случайные леса и градиентный бустинг деревьев.
Преодоление размерностного барьера
Совершенно естественно, чем больше данных, тем больше информации можно извлечь. Следовательно, при прочих равных условиях больше данных должно приводить к лучшим моделям, или, по крайней мере, к моделям, не уступающим своим предшественникам. В конце концов, если больше данных ухудшает модель, всегда можно в крайнем случае просто их проигнорировать. Однако из-за проблем переобучения отказ от данных оставался решением «наименьшего зла» до конца 1990-х годов. Именно суть проблемы «размерностного барьера». Эта ситуация была как озадачивающей, так и глубоко неудовлетворительной. Прорывы в 1990-х годах с потрясающими теоретическими и практическими озарениями разрушили размерностные барьеры. В результате эти прорывы на десятилетие вывели из строя всю область исследований, задержав появление её преемников, прежде всего методов глубокого обучения, обсуждаемых в следующем разделе.
Чтобы лучше понять, что раньше было не так с наличием большего количества данных, рассмотрим следующий сценарий: вымышленный производитель хочет прогнозировать количество незапланированных ремонтов в год для крупного промышленного оборудования. После тщательного анализа проблемы инженерная команда выявила три независимых фактора, которые, по-видимому, способствуют уровню отказов. Однако вклад каждого из факторов в общий уровень отказов остается неясным.
Таким образом, предлагается простая модель линейной регрессии с 3 входными переменными. Эта модель может быть записана как Y = a1 * X1 + a2 * X2 + a3 * X3, где
- Y — это выход модели линейной регрессии (уровень отказов, который инженеры хотят прогнозировать)
- X1, X2 и X3 — это три фактора (конкретные виды нагрузок, выраженные в часах работы), которые могут способствовать отказам
- a1, a2 и a3 — это три параметра модели, которые необходимо определить.
Количество наблюдений, необходимых для получения «достаточно хороших» оценок трёх параметров, во многом зависит от уровня шума в данных и от того, что считается «достаточно хорошим». Однако, интуитивно, для подгонки трёх параметров требуется как минимум две дюжины наблюдений, даже в самых благоприятных условиях. Когда инженерам удаётся собрать 100 наблюдений, они успешно оценивают 3 параметра, и полученная модель кажется «достаточно хорошей» для практического применения. Модель не учитывает многие аспекты этих 100 наблюдений, что делает её весьма приблизительной, но когда эту модель проверяют в других ситуациях через мысленные эксперименты, интуиция и опыт подсказывают инженерам, что модель ведёт себя вполне разумно.
Основываясь на первом успехе, инженеры решают провести более глубокое исследование. На этот раз они используют весь спектр электронных датчиков, встроенных в оборудование, и с помощью электронных записей, создаваемых этими датчиками, им удаётся увеличить набор входных факторов до 10 000. Изначально набор данных состоял из 100 наблюдений, каждое из которых характеризовалось 3 числами. Теперь набор данных расширен: это всё те же 100 наблюдений, но в каждом наблюдении содержится 10 000 чисел.
Однако, когда инженеры пытаются применить тот же подход к существенно обогащённому набору данных, линейная модель перестаёт работать. Поскольку имеется 10 000 измерений, линейная модель включает 10 000 параметров, а 100 наблюдений явно недостаточно для оценки такого числа параметров. Проблема не в том, что невозможно найти подходящие значения параметров, а наоборот: стало тривиально находить бесконечное множество наборов параметров, идеально соответствующих наблюдениям. Однако ни одна из этих «подогнанных» моделей не имеет практической пользы. Эти «большие» модели идеально описывают 100 наблюдений, но вне их модель становится бессмысленной.
Инженеры сталкиваются с проблемой размерности: казалось бы, число параметров должно оставаться небольшим по сравнению с числом наблюдений, иначе попытка моделирования разваливается. Эта проблема особенно досадна, поскольку «более крупный» набор данных с 10 000 измерениями, а не 3, явно содержит больше информации, чем меньший набор. Таким образом, адекватная статистическая модель должна быть способна учитывать эту дополнительную информацию, а не становиться нефункциональной при её наличии.
В середине 1990-х годов сообщество было потрясено двойным прорывом11 — как теоретическим, так и экспериментальным. Теоретическим прорывом стала теория Вапника–Червоненкиса (VC-тЕория)12. VC-теория доказала, что для определённых типов моделей реальную ошибку можно ограничить сверху суммой эмпирической ошибки и структурного риска, внутреннего свойства самой модели. В этом контексте «реальная ошибка» — это ошибка, наблюдаемая на данных, которых у вас нет, а «эмпирическая ошибка» — ошибка, наблюдаемая на данных, которые у вас есть. Минимизируя сумму эмпирической ошибки и структурного риска, можно минимизировать реальную ошибку, так как она оказывается «обособленной». Это стало одновременно поразительным результатом и, пожалуй, самым большим шагом к обобщению с момента выявления проблемы переобучения.
На экспериментальном фронте модели, впоследствии известные как опорные векторные машины (SVM), были представлены почти как учебное доказательство того, что VC-теория выявила в области обучения. Эти SVM стали первыми широко успешными моделями, способными эффективно использовать наборы данных, где число измерений превосходит число наблюдений.
Ограничив реальную ошибку — поистине удивительный теоретический результат — VC-теория сломала проблему размерности, которая оставалась неразрешённой почти на протяжении века. Это также открыло путь для моделей, способных использовать данные с высокой размерностью. Однако вскоре SVM были вытеснены альтернативными моделями, в первую очередь ансамблевыми методами (случайные леса13 и градиентный бустинг), которые в начале 2000-х доказали своё превосходство14 как в плане обобщения, так и в вычислительных требованиях. Как и замененные ими SVM, ансамблевые методы также обладают теоретическими гарантиями в отношении своей способности избегать переобучения. Все эти методы объединяет то, что они являются непараметрическими. Проблема размерности была преодолена благодаря моделям, которым не требовалось вводить один или более параметров для каждого измерения, таким образом обходя известный путь к проблемам переобучения.
Возвращаясь к проблеме незапланированных ремонтов, упомянутой ранее, в отличие от классических статистических моделей — таких как линейная регрессия, которая терпит неудачу при столкновении с проблемой размерности — ансамблевые методы смогли воспользоваться преимуществами большого набора данных и его 10 000 измерениями, несмотря на всего 100 наблюдений. Более того, ансамблевые методы практически сразу демонстрируют отличные результаты. Операционно это стало поистине замечательным развитием, поскольку устраняло необходимость кропотливо создавать модели, подбирая точно правильный набор входных измерений.
Влияние на более широкое сообщество, как в академической среде, так и за её пределами, оказалось огромным. Большая часть исследований в начале 2000-х годов была посвящена изучению этих непараметрических «поддерживаемых теорией» подходов. Однако успехи быстро угасали с течением времени. Фактически, спустя почти двадцать лет лучшие модели, относящиеся к перспективе статистического обучения, остаются прежними — просто с более производительными реализациями15.
Глубокий двойной спуск
До 2010 года общепринятое мнение гласило, что для избежания переобучения число параметров должно оставаться намного меньше числа наблюдений. Действительно, поскольку каждый параметр неявно представляет степень свободы, наличие такого же количества параметров, как наблюдений, гарантировало переобучение16. Ансамблевые методы обходили эту проблему, будучи непараметрическими. Однако это критическое предположение оказалось ошибочным, и весьма эффектным образом.
То, что позже стало известно как подход глубокого обучения, удивило почти всё сообщество гиперпараметрическими моделями. Эти модели не переобучаются, несмотря на то что содержат во много раз больше параметров, чем наблюдений.
Происхождение глубокого обучения является сложным и восходит к первым попыткам моделирования процессов мозга, а именно нейронных сетей. Детальный анализ этого происхождения выходит за рамки данного обсуждения, однако стоит отметить, что революция глубокого обучения в начале 2010-х годов началась как раз в тот момент, когда область отказалась от метафоры нейронных сетей в пользу механической симпатии. Реализации глубокого обучения заменили предыдущие модели намного более простыми вариантами. Эти новые модели использовали альтернативное вычислительное оборудование, в частности GPU (графические процессоры), которые, отчасти случайно, оказались хорошо приспособлены для операций линейной алгебры, характерных для моделей глубокого обучения17.
Понадобилось почти ещё пять лет, чтобы глубокое обучение было широко признано прорывом. Значительная часть скептицизма исходила от лагеря статистического обучения — иронично, именно от той части сообщества, которая два десятилетия назад успешно преодолела проблему размерности. Хотя объяснения этому скептицизму различны, очевидное противоречие между общепринятыми представлениями о переобучении и заявлениями о глубокому обучении, безусловно, способствовало значительному исходному уровню сомнений в отношении этого нового класса моделей.
Это противоречие оставалось практически неразрешённым до 2019 года, когда был выявлен глубокий двойной спуск18 — явление, характеризующее поведение определённых классов моделей. Для таких моделей увеличение числа параметров сначала ухудшает ошибку на тестовой выборке (из-за переобучения), пока число параметров не становится достаточно большим, чтобы изменить тенденцию и вновь улучшить тестовую ошибку. «Второй спуск» (ошибка на тестовой выборке) не был предсказан с точки зрения компромисса смещения и дисперсии.
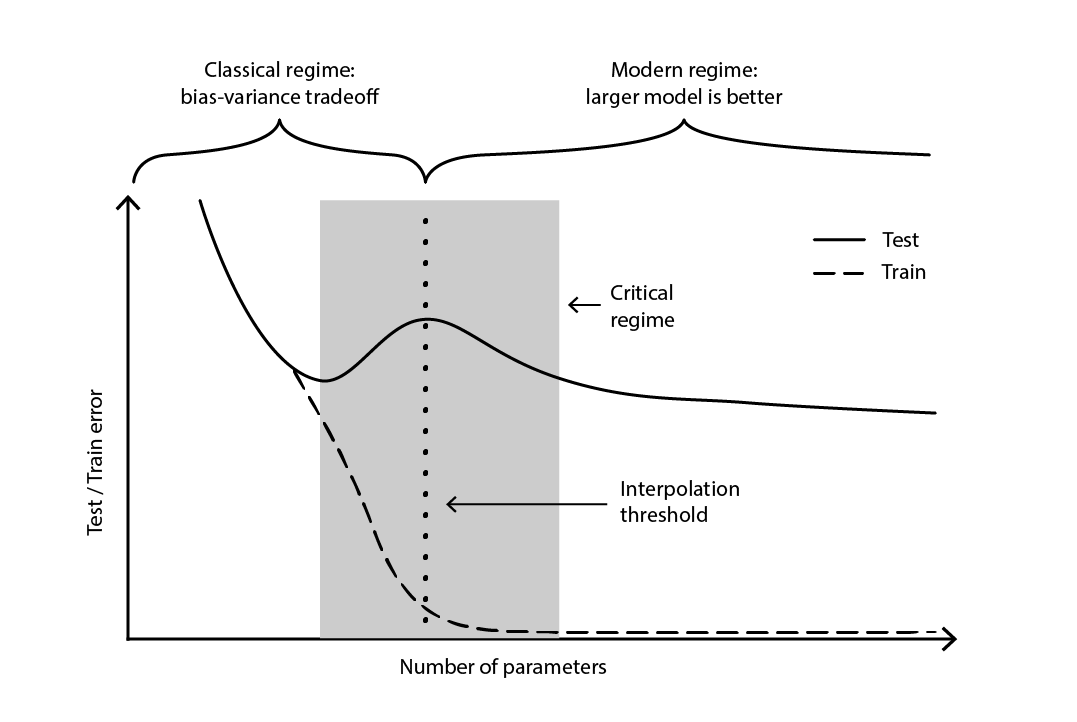
Рисунок 4. Глубокий двойной спуск.
Рисунок 4 иллюстрирует два последовательных режима, описанных выше. Первый режим — это классический компромисс между смещением и дисперсией, который, казалось бы, предполагает «оптимальное» число параметров. Однако этот минимум оказывается локальным. Существует второй режим, наблюдаемый при дальнейшем увеличении числа параметров, который демонстрирует асимптотическую сходимость к фактической оптимальной ошибке тестирования модели.
Глубокий двойной спуск не только примирил статистическую и глубокого обучения точки зрения, но и продемонстрировал, что обобщение остаётся относительно слабо понятным. Он доказал, что широко распространённые теории — доминировавшие до конца 2010-х — представляли искажённую картину обобщения. Однако глубокий двойной спуск пока не предоставляет рамок — или чего-то эквивалентного — которые могли бы предсказывать способность моделей к обобщению (или их неспособность) на основе их структуры. На сегодняшний день этот подход остаётся решительно эмпирическим.
Шипы цепочки поставок
Как было подробно рассмотрено, обобщение чрезвычайно сложно, а цепочки поставок добавляют свои уникальные особенности, ещё больше усугубляя ситуацию. Во-первых, данные, которые ищут специалисты по цепочке поставок, могут навсегда остаться недоступными; не просто частично невидимыми, а полностью необнаружимыми. Во-вторых, сам акт предсказания может изменить будущее, а достоверность предсказания, поскольку решения строятся на его основе, оказывается под вопросом. Таким образом, при решении проблемы обобщения в контексте цепочки поставок следует применять двухсторонний подход: с одной стороны — статистическая надежность модели, а с другой — высокоуровневое рассуждение, поддерживающее модель.
Кроме того, доступные данные не всегда совпадают с желательными данными. Рассмотрим производителя, который хочет прогнозировать спрос для определения объёма производства. Исторических данных о «спросе» не существует. Вместо этого исторические данные о продажах представляют собой лучший доступный показатель, отражающий исторический спрос. Однако исторические продажи искажены прошлым дефицитом товара. Нулевые продажи, вызванные дефицитом, не должны отождествляться с нулевым спросом. Хотя можно создать модель, способную преобразовать историю продаж в своего рода историю спроса, ошибка обобщения этой модели по своей природе ускользает, поскольку ни прошлое, ни будущее не содержат этих данных. Короче говоря, «спрос» — это необходимая, но неосязаемая концепция.
В терминологии машинного обучения моделирование спроса является задачей обучения без учителя, где выход модели никогда не наблюдается напрямую. Этот аспект обучения без учителя осложняет работу большинства алгоритмов обучения, а также большинство методов валидации моделей — по крайней мере, в их «наивном» варианте. Более того, он подрывает саму идею соревнования по прогнозированию, подразумевающего простой двухэтапный процесс, при котором исходный набор данных разбивается на публичную (тренировочную) и частную (валидационную) подвыборки. Сама валидация становится необходимым этапом моделирования.
Проще говоря, предсказание, сделанное производителем, так или иначе сформирует будущее, с которым он столкнется. Высокий прогнозируемый спрос означает, что производитель увеличит объёмы производства. Если бизнес управляется эффективно, в производственном процессе, скорее всего, будут достигнуты эффекты масштаба, что приведёт к снижению производственных затрат. В свою очередь, производитель, скорее всего, воспользуется этими новыми экономическими преимуществами для снижения цен, приобретая конкурентное преимущество перед соперниками. Рынок, стремящийся выбрать самый дешёвый вариант, может быстро принять этого производителя как наи конкурентоспособнейшего, что приведёт к всплеску спроса, значительно превышающему первоначальный прогноз.
Это явление известно как самосбывающееся пророчество — предсказание, которое сбывается благодаря вере участников в само предсказание. Нетрадиционная, но не совсем необоснованная точка зрения могла бы характеризовать цепочки поставок как гигантские самосбывающиеся устройства в стиле Руба Голдберга. На методологическом уровне это переплетение наблюдателя и наблюдения ещё больше усложняет ситуацию, поскольку обобщение связано с улавливанием стратегического намерения, лежащего в основе развития цепочки поставок.
На данном этапе задача обобщения, как она представлена в цепочке поставок, может показаться непреодолимой. Электронные таблицы, которые остаются повсеместными в цепочках поставок, безусловно, указывают на то, что это положение (пусть и неявное) является стандартным для большинства компаний. Однако таблица прежде всего является инструментом для отсрочки решения проблемы на основе разовых человеческих суждений, а не применения какой-либо систематической методики.
Хотя полагаться на человеческое суждение само по себе всегда является неправильным ответом, это также не удовлетворяет проблему. Наличие дефицита товаров не означает, что в отношении спроса действует принцип всё возможно. Конечно, если производитель поддерживал средний уровень сервиса выше 90% в течение последних трёх лет, маловероятно, что (наблюдаемый) спрос мог бы быть в 10 раз выше продаж. Таким образом, разумно ожидать, что можно разработать систематический метод для борьбы с такими искажениями. Аналогично, самосбывающееся пророчество также можно смоделировать, прежде всего через понятие политики, как его понимает теория управления.
Таким образом, при рассмотрении реальной цепочки поставок обобщение требует двухстороннего подхода. С одной стороны, модель должна быть статистически обоснованной в той мере, в какой позволяют обширные науки об обучении. Это включает не только теоретические подходы, такие как классическая статистика и статистическое обучение, но также и эмпирические методы, такие как машинное обучение и соревнования по прогнозированию. Возврат к статистике XIX века не является разумным предложением для управления цепями поставок.
Во-вторых, модель должна опираться на высокоуровневое рассуждение. Другими словами, для каждого компонента модели и каждого шага процесса моделирования должно быть обоснование, которое имеет смысл с точки зрения цепочки поставок. Без этого ингредиента практически гарантирован оперативный хаос19, обычно вызванный эволюцией самой цепочки поставок, её операционной экосистемы или лежащего в её основе ландшафта приложений. Суть высокоуровневого рассуждения не в том, чтобы модель сработала один раз, а в том, чтобы она эффективно функционировала в течение нескольких лет в постоянно меняющейся среде. Именно это рассуждение является не таким уж секретным ингредиентом, который помогает принять решение о том, что пришло время пересмотреть модель, когда её проект, каким бы он ни был, уже не соответствует реальности и/или бизнес-целям.
На первый взгляд это утверждение может показаться уязвимым для ранее высказанной критики в адрес электронных таблиц – критики против передачи сложной работы какому-то неуловимому «человеческому суждению». Хотя в этом утверждении оценка модели по-прежнему возлагается на человеческое суждение, исполнение модели предусмотрено как полностью автоматизированное. Таким образом, ежедневные операции должны выполняться полностью автоматически, даже если текущие инженерные усилия по дальнейшему совершенствованию числовых рецептов таковыми не являются.
Заметки
-
Существует важная алгоритмическая техника под названием «мемоизация», которая именно заменяет результат, который мог бы быть вычислен заново, на его предварительно вычисленную версию, тем самым обменяя дополнительные затраты памяти на меньшие вычислительные затраты. Однако эта техника не имеет отношения к данному обсуждению. ↩︎
-
Почему большинство опубликованных результатов исследований ошибочны, John P. A. Ioannidis, август 2005 ↩︎
-
С точки зрения прогнозирования временных рядов понятие обобщения рассматривается через призму «точности». Точность можно рассматривать как частный случай обобщения при анализе временных рядов. ↩︎
-
Makridakis, S.; Andersen, A.; Carbone, R.; Fildes, R.; Hibon, M.; Lewandowski, R.; Newton, J.; Parzen, E.; Winkler, R. (Апрель 1982). «Точность методов экстраполяции (временных рядов): результаты конкурса по прогнозированию». Journal of Forecasting. 1 (2): 111–153. doi:10.1002/for.3980010202. ↩︎
-
Kaggle in Numbers, Carl McBride Ellis, получено 8 февраля 2023, ↩︎
-
Отрывок 1935 года «Возможно, мы устарели, но для нас анализ с шестью переменными, основанный на тринадцати наблюдениях, кажется переобучением» из “The Quarterly Review of Biology” (сентябрь 1935, том 10, № 3, стр. 341–377) свидетельствует о том, что концепция переобучения в статистике была уже устоявшейся. ↩︎
-
Grenander, Ulf. Об эмпирическом спектральном анализе стохастических процессов. Ark. Mat., 1(6):503–531, 08 1952. ↩︎
-
Whittle, P. Тесты соответствия во временных рядах, том 39, № 3/4 (декабрь 1952), стр. 309-318] (10 страниц), Oxford University Press ↩︎
-
Everitt B.S., Skrondal A. (2010), Кембриджский словарь статистики, Cambridge University Press. ↩︎
-
Асимптотические преимущества использования больших значений k в k-кратной валидации можно вывести из центральной предельной теоремы. Этот вывод намекает, что, увеличивая k, мы можем приблизиться примерно на 1/sqrt(k) к исчерпанию всего потенциала улучшения, который изначально предлагал k-кратный метод. ↩︎
-
Сети опорных векторов, Corinna Cortes, Vladimir Vapnik, Machine Learning, том 20, стр. 273–297 (1995) ↩︎
-
Теория Vapnik–Chervonenkis (VC) была не единственным кандидатом для формализации понятия «обучения». Рамочная концепция PAC (probably approximately correct, вероятно, примерно правильная) Валянта 1984 года проложила путь для формальных подходов к обучению. Однако концепция PAC не обладала той огромной популярностью и операционными успехами, которыми пользовалась теория VC в период около тысячелетия. ↩︎
-
Случайные леса, Leo Breiman, Machine Learning, том 45, стр. 5–32 (2001) ↩︎
-
Одним из неприятных последствий того, что методы опорных векторов (SVM) были сильно вдохновлены математической теорией, является то, что эти модели обладают слабой «механической симпатией» к современному вычислительному оборудованию. Относительная неадекватность SVM для обработки больших наборов данных – включая миллионы наблюдений или более – по сравнению с альтернативами и предопределила упадок этих методов. ↩︎
-
XGBoost и LightGBM — две реализации ансамблевых методов с открытым исходным кодом, которые остаются широко популярными в кругах специалистов по машинному обучению. ↩︎
-
В целях краткости здесь происходит небольшое упрощение. Существует целая область исследований, посвящённая «регуляризации» статистических моделей. При наличии ограничений регуляризации количество параметров, даже в классической модели, такой как линейная регрессия, может с уверенностью превосходить число наблюдений. В условиях регуляризации ни одно значение параметра уже не представляет собой полную степень свободы, а лишь её долю. Таким образом, правильнее говорить о числе степеней свободы, а не о числе параметров. Поскольку эти косвенные соображения не меняют принципиально представленные здесь взгляды, упрощённой версии достаточно. ↩︎
-
На самом деле причинно-следственная связь обратная. Пионеры глубокого обучения сумели преобразовать свои исходные модели — нейронные сети — в более простые модели, основанные почти исключительно на линейной алгебре. Суть этого преобразования заключалась именно в том, чтобы сделать возможным запуск этих новых моделей на вычислительном оборудовании, которое обменивало универсальность на сырую мощность, а именно на GPU. ↩︎
-
Deep Double Descent: когда большие модели и большие объемы данных вредят, Preetum Nakkiran, Gal Kaplun, Yamini Bansal, Tristan Yang, Boaz Barak, Ilya Sutskever, декабрь 2019 ↩︎
-
Подавляющее большинство инициатив в области data science в цепочке поставок терпят неудачу. Мои случайные наблюдения свидетельствуют о том, что незнание специалистом по данным того, что заставляет цепочку поставок работать, является коренной причиной большинства этих неудач. Хотя для недавно обученного специалиста по данным чрезвычайно заманчиво использовать новейший и самый блестящий пакет машинного обучения с открытым исходным кодом, не все методы моделирования одинаково подходят для поддержки высокоуровневого рассуждения. На самом деле, большинство «основных» методов оказываются просто ужасными, когда речь заходит о процессе объяснения работы модели (whiteboxing). ↩︎