Непрерывный ранжированный вероятностный скор (CRPS)
Вероятностные прогнозы присваивают вероятность каждому возможному будущему. Однако не все вероятностные прогнозы одинаково точны, и требуются метрики для оценки точности различных вероятностных прогнозов. Простые метрики точности такие как MAE (средняя абсолютная ошибка) или MAPE (средняя абсолютная процентная ошибка) не применимы напрямую к вероятностным прогнозам. Непрерывный ранжированный вероятностный скор (CRPS) обобщает MAE для случая вероятностных прогнозов. Наряду с перекрестной энтропией CRPS является одной из наиболее широко используемых метрик точности, когда речь идет о вероятностных прогнозах.
Обзор
CRPS часто используется для оценки точности двух моделей вероятностного прогнозирования. В частности, эту метрику можно комбинировать с процессом ретроспективного тестирования, чтобы стабилизировать оценку точности путем использования множества измерений на одном и том же наборе данных.
Эта метрика существенно отличается от более простых метрик, таких как MAE, из-за своей асимметричной формы: в то время как прогнозы являются вероятностными, наблюдения детерминированы. В отличие от функции потерь пинбола, CRPS не сосредотачивается на какой-либо конкретной точке распределения вероятностей, а рассматривает распределение прогнозов в целом.
Формальное определение
Пусть $${X}$$ – случайная величина.
Пусть $${F}$$ – функция распределения (CDF) случайной величины $${X}$$, такая что $${F(y)=\mathbf{P}\left[X \leq y\right]}$$.
Пусть $${x}$$ – наблюдение, а $${F}$$ – функция распределения, связанная с эмпирическим вероятностным прогнозом.
CRPS между $${x}$$ и $${F}$$ определяется как:
где $${𝟙}$$ – функция Хевисайда, обозначающая ступенчатую функцию вдоль действительной оси, которая принимает следующие значения:
- значение 1, если действительный аргумент положительный или равен нулю,
- значение 0 в противном случае.
CRPS выражается в тех же единицах, что и наблюдаемая величина (например, если спрос на продукт прогнозируется в единицах, то и CRPS будет выражаться в единицах).
CRPS обобщает среднюю абсолютную ошибку (MAE). Более того, если прогноз детерминирован, он сводится к MAE. Этот момент иллюстрируется на диаграмме D ниже.
Известные свойства
Гнайтинг и Рафферти (2004) показывают, что непрерывный ранжированный вероятностный скор можно записать эквивалентно следующим образом:
где
- $${X}$$ и $${X^*}$$ – независимые копии линейной случайной величины,
- $${X}$$ – случайная величина, связанная с функцией распределения $${F}$$,
- $${\mathbf{E} }$$ – математическое ожидание $${X}$$.
Численный расчет
С числовой точки зрения, простой способ вычисления CRPS состоит в разбиении исходного интеграла на два интеграла с подобранными границами для упрощения функции Хевисайда, что дает:
На практике, поскольку $$F$$ является эмпирическим распределением, полученным с помощью модели прогнозирования, соответствующая случайная величина $${X}$$ имеет компактную область значений, что означает, что существует только конечное число точек, где $${\mathbf{P}[X = x] \gt 0}$$. Также все значения $$x$$ являются дискретными числами. Таким образом, интегралы можно заменить на дискретные конечные суммы, как иллюстрируется формулой ниже и диаграммой B в следующем разделе.
В формуле (4) индекс $$n$$ обозначает последний элемент правой хвостовой части распределения вероятностей (например, наивысшее значение спроса с ненулевой вероятностью).
Наконец, поскольку вычисление CRPS проводится для одной временной точки, для вычисления CRPS за определенный период оценки (например, для окна ответственности, которое представляет собой сумму срока поставки и периода пополнения запасов) следует взять среднее значение соответствующих расчетных CRPS за этот период.
Визуальная интуиция
Чтобы проиллюстрировать вычисление CRPS, рассмотрим следующий пример (см. диаграммы ниже):
A: Изначально мы построили вероятностный прогноз спроса, используя отрицательное биномиальное распределение и усекли его хвосты при вероятностях менее 0.1% (что представляет собой крайне маловероятные события, такие как те, что случаются примерно раз в три года). Прогнозируемые значения спроса с ненулевой вероятностью охватывали диапазон от 1 до 26 единиц. Позже оказалось, что фактический спрос составил 15 единиц (как показано вертикальной красной пунктирной линией).
B: Мы вычислили CRPS согласно формуле (4) выше (см. раздел “Численный расчет”). Полученное значение CRPS представляет собой сумму двух областей, залитых светло-красным цветом.
C: То же, что и диаграмма A, но с добавлением точечного прогноза для сравнения.
D: Применение вычисления CRPS к точечному прогнозу демонстрирует, что когда CRPS применяется к точечному прогнозу, результатом является метрика MAE. Действительно, точечные прогнозы являются тривиальной формой вероятностных прогнозов, где мы неявно назначаем 100% вероятность одному значению. Тогда график накопленной вероятности для CRPS будет представлен двумя ступенчатыми функциями – одной для точечных прогнозов и одной для фактического спроса. Это означает, что в зависимости от относительного положения точечного прогноза и фактического значения, одна из двух сумм в формуле CRPS (4) станет нулевой: первая сумма для переоценок и вторая для недооценок.
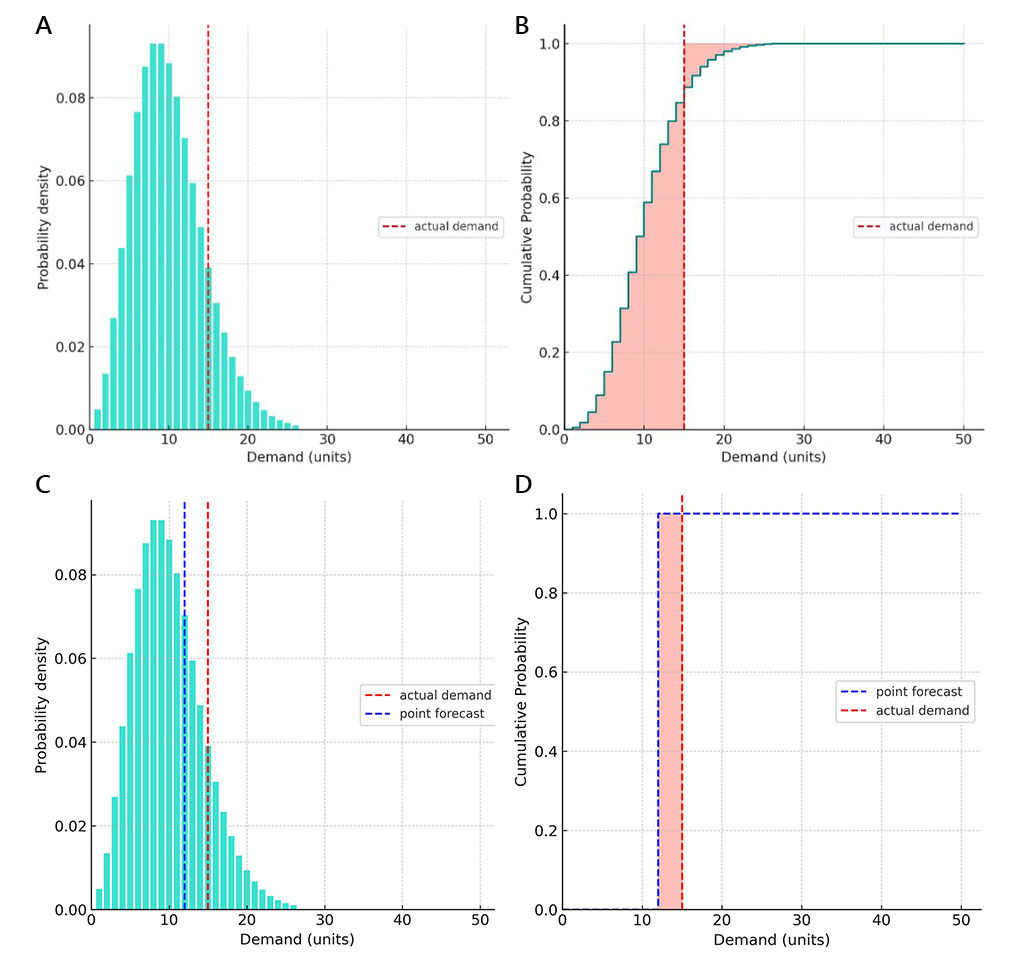
Для приведенного примера с этими 4 диаграммами полученные значения CRPS для вероятностного прогноза и точечного прогноза составляют 3.32 и 3 соответственно. Глядя на эти числа, можно было бы заключить, что точечный прогноз более точный, поскольку его метрика точности меньше (лучше), чем у вероятностного прогноза. Однако такое заключение неверно.
В приведенном примере мы рассмотрели только одно значение фактического спроса, однако когда вероятностный прогноз обучается на исторических данных, вероятности корректируются в соответствии с частотой появления соответствующих значений спроса (с учетом значений, доступных в обучающем наборе данных). Если они выбраны правильно, то среднее значение CRPS для тестового набора данных будет сопоставимо со значением для обучающего/валидационного набора, поскольку прогноз адекватно отразит частоту появления различных значений спроса в тестовых данных.
Ниже приведенная диаграмма демонстрирует превосходство вероятностных прогнозов по сравнению с точечными.
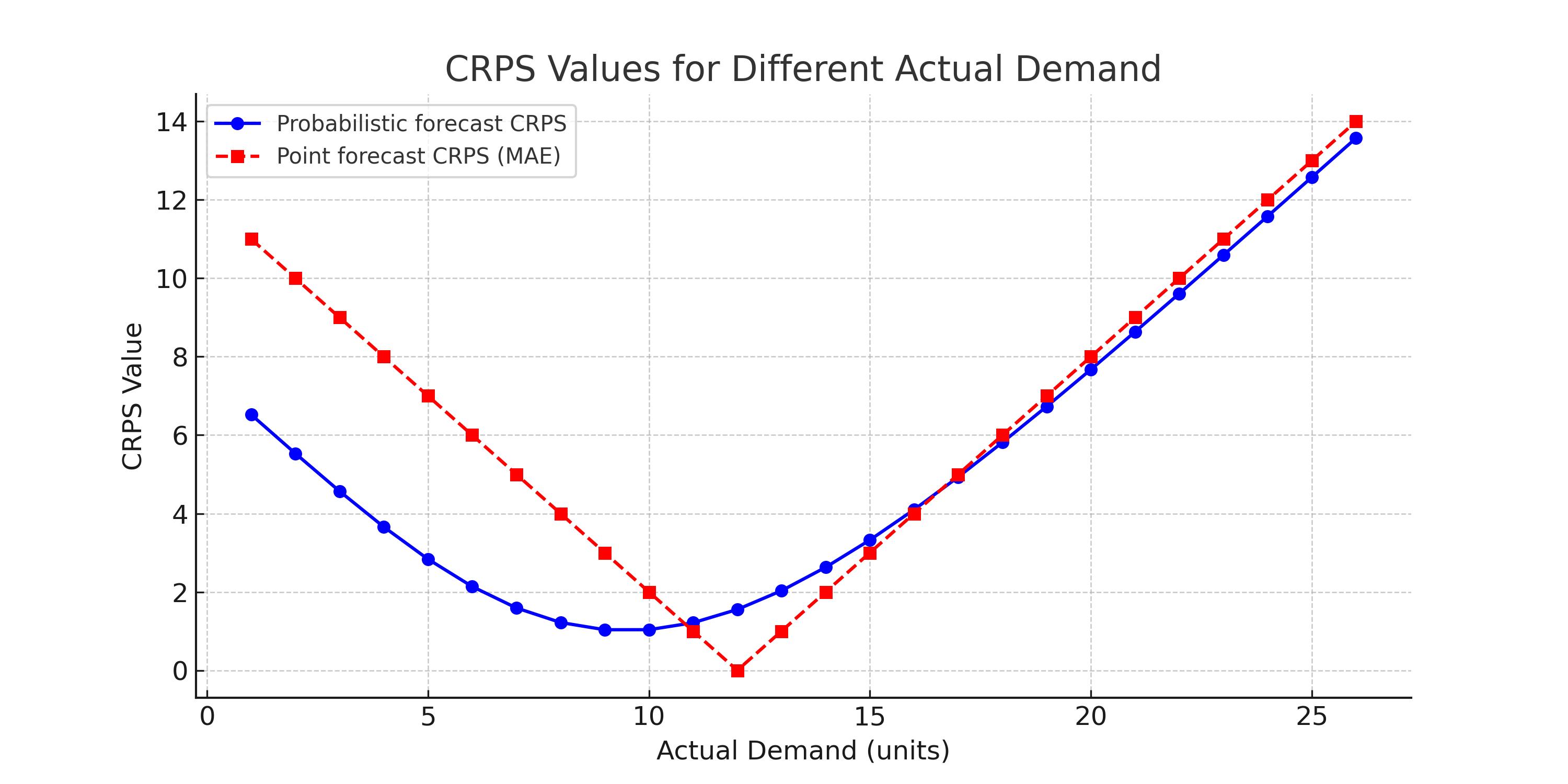
Обратите внимание, как плавно меняется CRPS в зависимости от различных фактических значений. Также отметьте, что за исключением небольшой области (где точечный прогноз очень близок к фактическому значению), во всех остальных случаях CRPS для вероятностных прогнозов меньше, чем для точечных прогнозов.
Если у нас было бы несколько различных точечных прогнозов, это наблюдение оставалось бы верным. Нужно было бы мысленно сдвигать красную кривую влево или вправо в зависимости от точечного предсказания, но превосходство вероятностного прогнозирования все равно оставалось бы подтвержденным.
Литература
Гнайтинг, Т. и Рафферти, А. Е. (2004). Строго корректные правила оценки, прогнозирование и оценка. Технический отчет №463, Кафедра статистики, Вашингтонский университет, Сиэтл, Вашингтон, США.