ピンボール損失関数

ピンボール損失関数、別名分位損失と呼ばれるものは、分位予測の精度を評価するための指標です。

分位予測の精度を評価することは、分位予測において微妙な問題です。実際、従来の予測では予測値を実測値にできるだけ近づけることが目的ですが、分位予測の場合、状況は意図的に_偏って_います。したがって、単純な実測値対予測値の比較は十分ではありません。ピンボール損失関数は、分位予測モデルの_精度_として解釈できる値を返します.

数式

目標の分位数を$${\tau}$$、実際の値を$${y}$$、分位予測を$${z}$$とすると、ピンボール損失関数$${L_\tau}$$は次のように表されます:

ダウンロード： pinball-loss-function.xlsx

このスプレッドシートは、Microsoft Excel内でピンボール損失関数を計算する方法を示しています。実際の数式は、MAPEなどの多くの精度指標と比べてもそれほど複雑ではありません.

図解

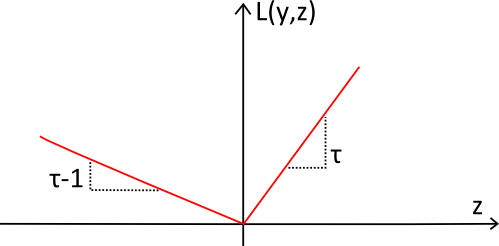
ピンボール損失関数（赤色）は、その形状がピンボールのボールの軌道に似ていることから名付けられました。この関数は常に正の値を取り、目標値$${y}$$から離れるほど、$${L_\tau(y,z)}$$の値は大きくなります。分位予測における希望する不均衡を反映するために、傾きが用いられます.

最適な分位モデルは最小のピンボール損失を示す

ピンボール損失関数に関連する最も重要な結果は、ピンボール損失が低ければ低いほど、より精度の高い分位予測となるという点です.

したがって、2つの分位モデル（たとえばLokadとその他）の精度を比較するには、統計的に有意な差があると確認できるだけの十分な数の時系列に対して各モデルの平均ピンボール損失を計算すれば十分です。実際、数百の時系列でどの分位モデルが最も精度が高いかを評価することが可能です.

Lokadの落とし穴

古典的な予測（すなわち平均予測）における精度という概念の単純さは、実際には過大評価されていると私たちは考えます。平均予測も分位予測も同様に、過剰適合の影響を受け、そのため予測モデルの比較が非常に複雑になります。しかし、ピンボール損失関数は、2つの分位予測モデルの相対的な精度を評価するための非常にシンプルな方法を提供します.

関連文献

• 時系列の逐次分位予測、2011年3月、Gerard Biau と Benoit Patra著、Information Theory, IEEE Transactions
• 連続ランク付け確率スコア (CRPS)、確率予測におけるピンボール損失関数の一般化