エクセルでの確率的予測を用いた優先順位付き在庫補充
不確実性は予測における本質的かつ解消不可能な側面です。しかし、20世紀には十分な数学モデルがあれば不確実性を排除できるとの希望の下、統計的予測が登場しました。その結果、初期のサプライチェーン理論では、不確実性が新しいまたは better forecasting 技術で解消されるか、もしくは重要でなくなると見做され、軽視または否定されました。善意であったものの、これらのアプローチは欠陥があり、統計モデリングの1世紀を経てもなお、不確実性は頑なに残っています。2012年、Lokadは代替の supply chain perspective を先駆けて提案し、不確実性を受け入れ定量化する手法を打ち出しました。このアプローチは、従来のポイントベースの予測ではなく、probabilistic forecasts を活用し、time-series の予測と比較されます。さらに、本ガイドおよび付属の Microsoft Excel スプレッドシートでは、在庫 replenishment 問題に対して確率的予測を適用しています。これにより、Excel を用いた優先順位付き在庫補充ポリシーが実現されます。我々の目的は、より高度なソフトウェアツールに不慣れな読者にもこのアプローチを普及させることと、不確実性を受け入れるためには洗練されたツールよりも特定の考え方が必要であることを示すことの二点にあります。
Download: probabilistic-inventory-replenishment.xlsx
1. 在庫補充問題
在庫補充問題は、企業の主要な財務的制約と目標を考慮に入れた最適な購入リストの特定に焦点を当てています。このリストを作成する手法は、投資した1ドルごとの投資収益率を最大化することを試みるため、予算の制約に関係なく同様に機能するはずです。問題は、すべての SKUs が同じ資金を巡って競合しているため、各SKUの在庫単位の財務的リターンを、他のすべてのSKUの追加単位と比較して定量化しランク付けする必要がある点にあります。
1.1 優先順位付き在庫補充ソリューション
上述の通り在庫のランク付けにはミクロな視点が必要です。購入リストにSKUの任意の単位を追加した際のリターンを比較するためには、確率的需要予測で示される販売確率 と 例えば粗利益率や購入価格などの economic drivers など、いくつかの要因を考慮する必要があります。各数量は、限られた warehouse 容量、ロット乗数、MOQ/MOVなどの内部および外部の制約と釣り合わされなければなりません。さらに、2つ以上の単位が同等の期待収益を示すエッジケースは、各製品の 相対的重要度 の評価を通じて在庫補充ポリシーに組み入れる必要があります。SKUは個別に捉えるのではなく、バスケットとして考慮すべきです。たとえば、単独では利益率が低い(牛乳など)SKUであっても、高利益率製品の販売を促進するためにより重要とされる場合があります。このように、他の販売を補助する低利益製品の service levels を維持するための財務的報酬は、別の要因(「stockout cover」)を表します。確率的予測を入力として活用する優先順位付き在庫補充(PIR)アプローチは、上記のすべての要因を考慮に入れます。
要するに、PIRソリューションは3つのステップに要約できます:
1. 確率的需要予測を構築する。
2. すべての実現可能な購買数量を一覧にする。
3. 経済的ドライバーを用いてすべての実現可能な購買数量をランク付けする。
1.2 エクセルでの優先順位付き在庫補充
前節で挙げた経済的ドライバーを含む架空の店舗の財務データを利用して、このExcelスプレッドシートは3つのSKU(ペン、キーボード、ブックケース)1の在庫補充ポリシーをモデル化します。SKUの追加単位ごとの財務的影響(注文した場合)とその販売確率は、Charts シートに示されています(図1参照)。図やチャートは、Control Tower シート(図2)の入力値やモデルの仮定(初期在庫水準、購入・販売価格など)に応じて更新されます。Micro purchasing decisions シート(図3)では、主要な入力値に基づいて実現可能な意思決定オプションの詳細な一覧が生成されます。これらの入力は、Distribution generators シート(図4)の確率的需要予測および Control Tower シートから得られます。最後に、期待される投資収益率に基づいてランク付けされた優先順位付き在庫補充の意思決定表がまとめられます(図5の Ranked purchasing decisions シート参照)。
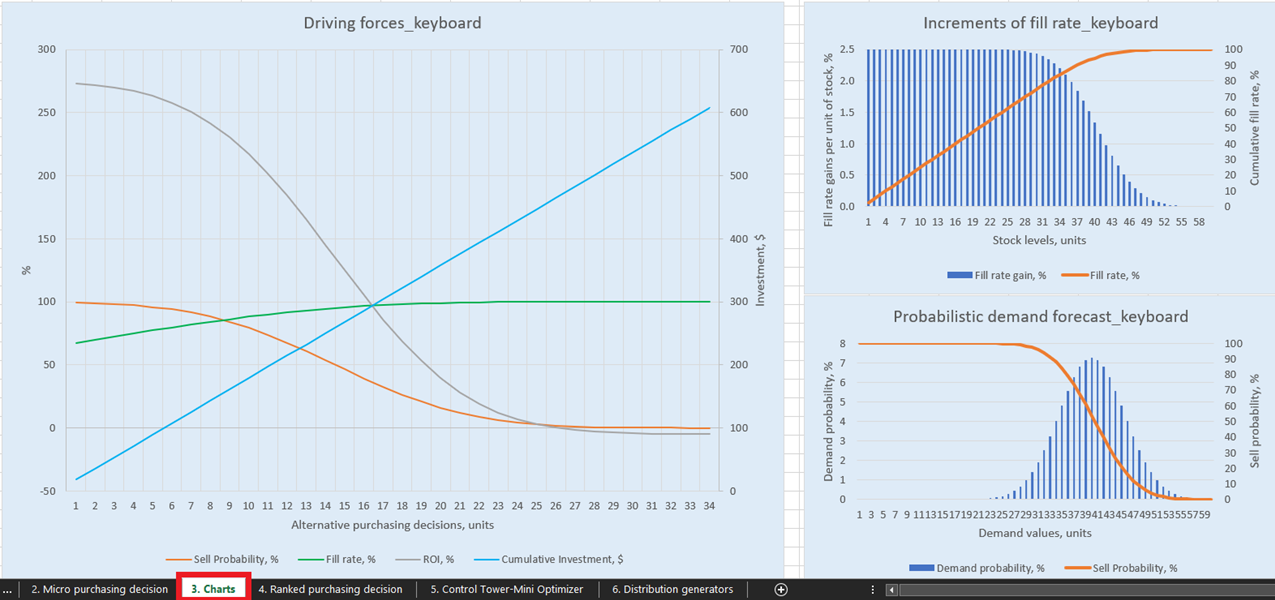
図 1. Charts 内の「Driving forces keyboard」の表示。該当箇所は赤でハイライトされています。
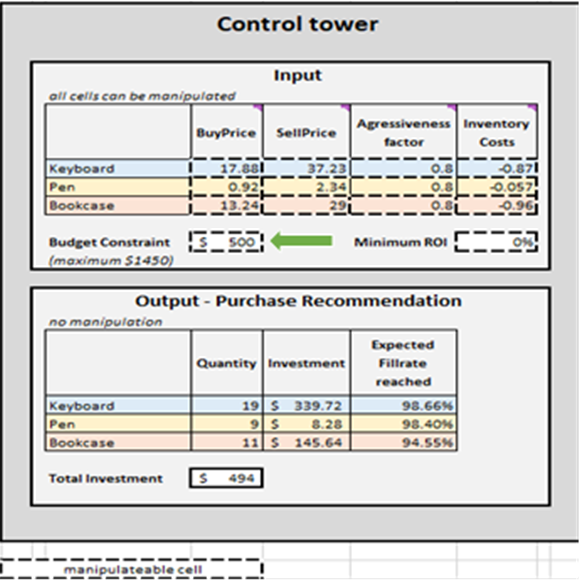
図 2. Control Tower 内に位置する「Control Tower」– Mini Optimizer(シート5)。「Budget Constraint」は$0から$1450の間で任意の値に編集可能です(緑の矢印参照)。
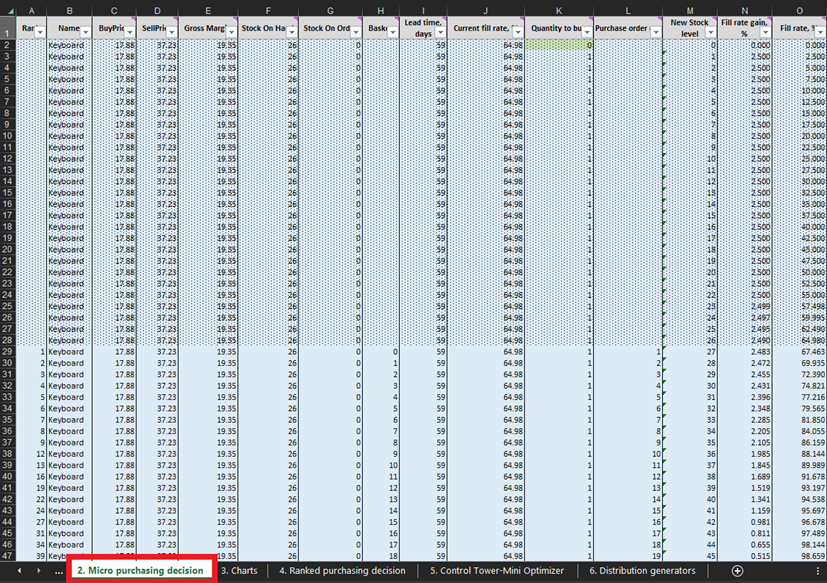
図 3. Excel内でのMicro purchasing decisions の配置場所(赤でハイライト)。条件付きの点線フォーマットで覆われた行は、過去のデータ(上記画像の28行目までを含む)を示しており、以前の購買決定を表しています。ここでは条件付きフォーマット以下の部分のみが対象です。同様の点線フォーマットがペンおよびブックケースのデータにも適用されています。
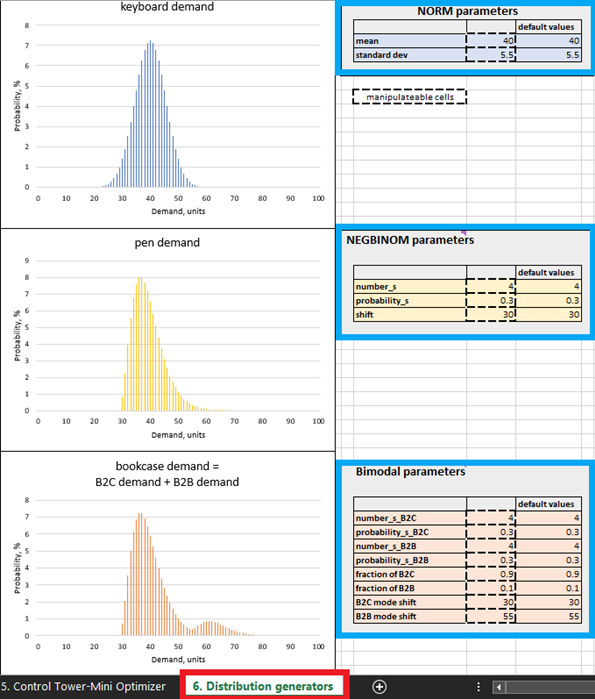
図 4. Excel内でのDistribution generators の配置場所(赤でハイライト)。製品コントロールパネルは青でハイライトされ、破線の輪郭があるセルは操作可能です。
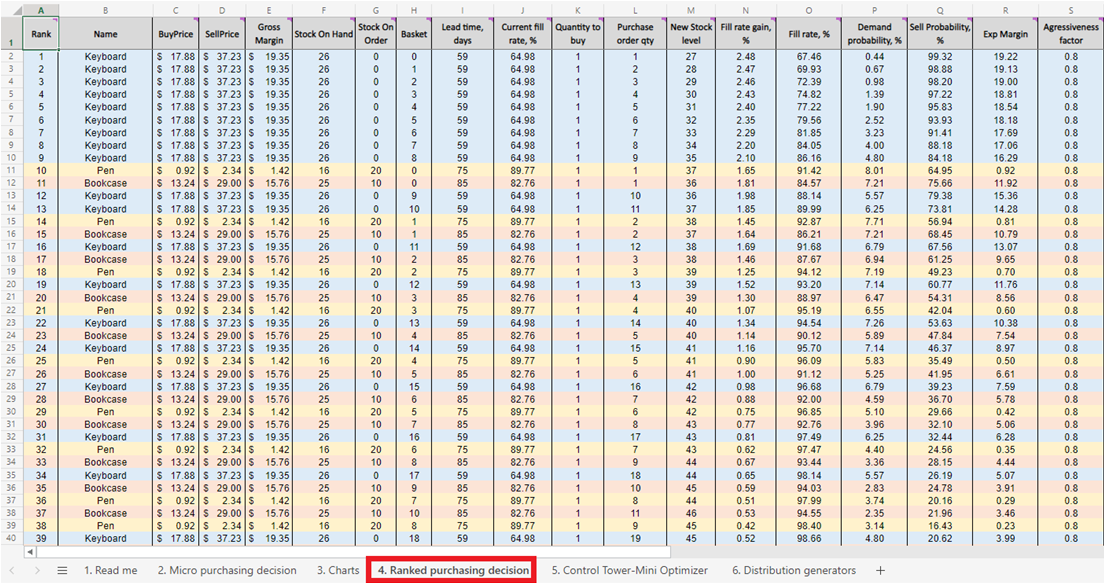
図 5. シート4に位置する、優先順位付き在庫補充のためのミクロ購買決定リスト。
2. 確率的需要予測
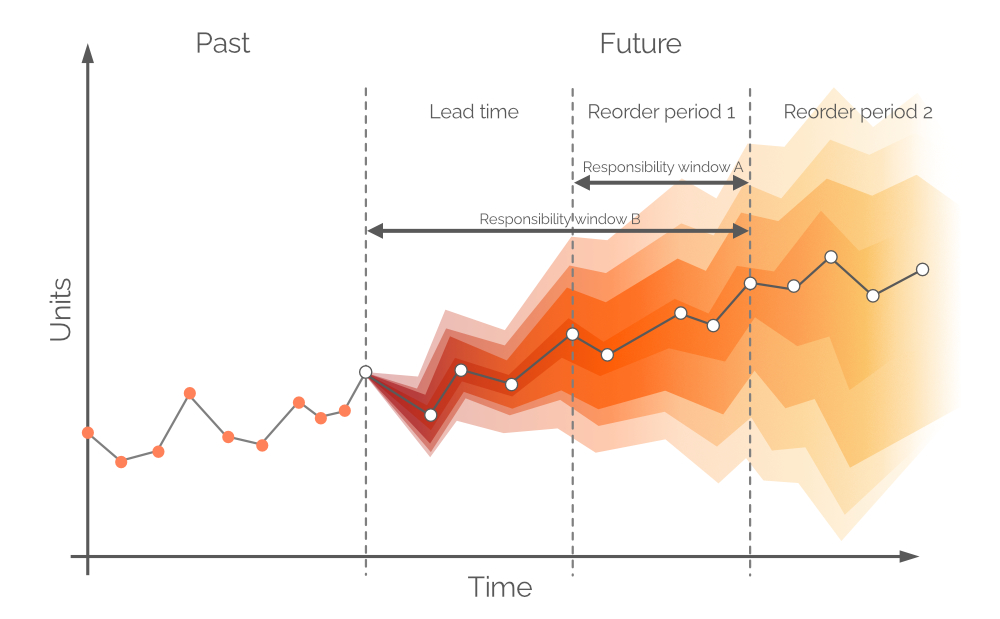
ここでいう確率的予測とは、将来の需要の 可能性のある 値とその確率の全体集合を意味します。これは将来需要の内在的な不確実性を受け入れ、任意の期間で構築することが可能です。従来の時系列予測と同様に、最も可能性の高い需要値(図6の白い点)が識別され、これらを結ぶ傾向線も描かれます。しかし、確率的予測は、あらゆる可能な(ただし同等の確率ではない)需要値を加えることで不確実性を統合しています。このアプローチは、異なる信頼区間が異なる確率の需要値を表す図6に示されています。
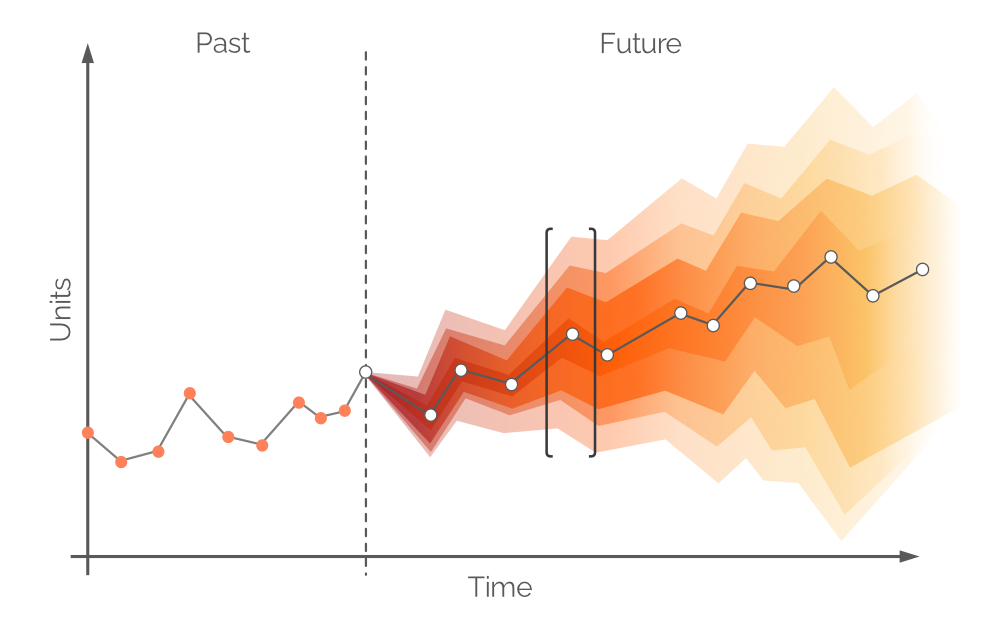
図 6. 確率的予測(y軸:需要、x軸:時間)。点線の垂直な灰色の線は現在の時刻(「now」)を示しています。時間は日単位で測定されていますが、任意の間隔にすることが可能です。黒い括弧で囲まれた領域については後述します。
図6の白い点は、一定の将来間隔における最も可能性の高い需要値を表しています。これに伴い、代替の将来需要値の範囲を示すカラーバンド(色による確率分布)が表示されます。白い点から離れるにつれて垂直方向に色が薄くなり、これは不確実性の増大および確率の低下を示しています。全体として、時間の経過(水平軸に沿って)と共にカラーバンドは薄れていきますが、それでも常に 最も可能性の高い 値が存在し、これが白い点で表現されます。ある時点での確率分布の例が図7に示されています。
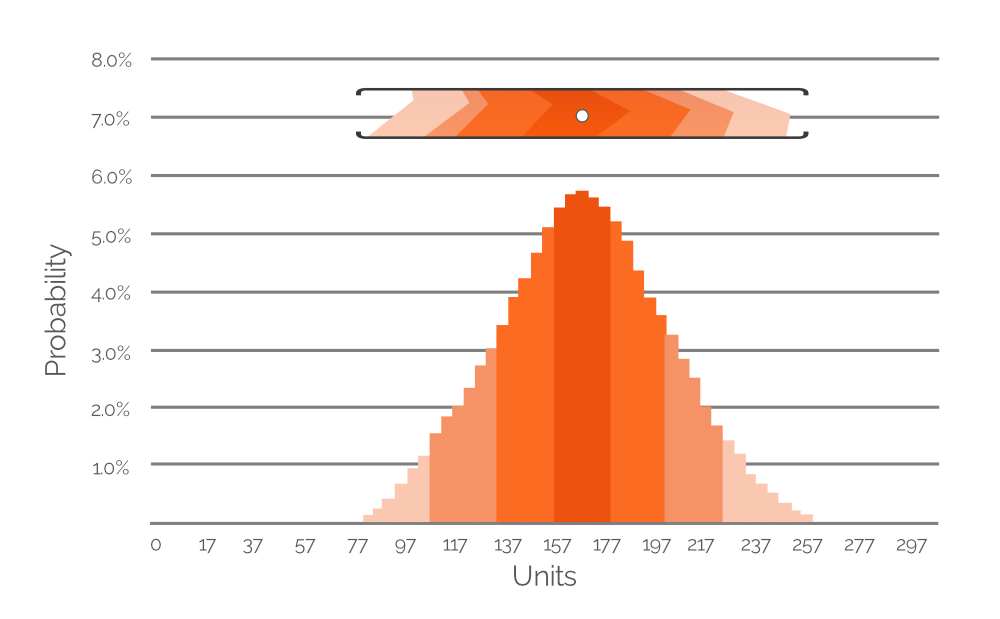
Figure 7. A histogram depicting the probability of several possible demand values (at 20-unit intervals). Y-axis is probability value; x-axis is demand in units. The histogram is a representation of the highlighted value range in Figure 6 (included here for reference purposes).
図7は、図6で強調されたデータを確率ヒストグラムとして表現しており、各需要値の確率を明確な数値で示しています。理解しやすさのためにカラーコーディングが保持されており(薄い色は確率が低く、濃い色は確率が高いことを示す)、この例では最も可能性の高い需要値がおよそ167単位(±)であるため、図6の切り抜かれた範囲の白い点がヒストグラムの最も高い棒の上に位置しています。しかし、非常に低い需要値および高い需要値(それぞれ約80単位と260単位、いずれも非常に薄いオレンジ色)にも確率が割り当てられており、これは確率的予測のデータの豊かさを示しています。同様のヒストグラムがExcelスプレッドシート内に各SKUごとに含まれており(図4参照)、これらのヒストグラムを用いることで、発生確率がゼロでない需要値(単位)を識別し、PIRに反映させることが可能となります。
2.1 確率的予測の構築
Excelで過去データを用いて 本物の 確率的予測を構築することは可能ですが、この目的にはExcelは最も適さないツールと言えます。生産グレードの確率的予測を構築する具体的な手法は本書の範囲外であるため、簡便さから合成確率的予測が採用されました。これらの合成予測のパラメータは、Distribution generators(図4参照)内で操作可能ですが、調整する前にまずデフォルト設定を確認することが推奨されます。
主流のサプライチェーン慣行では、需要は通常正規分布すると考えられていますが、実際にはほとんどのSKUが正規分布パターンから逸脱しています。この現実を踏まえ、わざと3種類の分布パターンを選定しました:正規分布(キーボード用)、負の二項分布(ペン用)および二峰性分布(ブックケース用―2つの負の二項分布の混合)。以下に、この仮定の根拠を示します。
例えば、ブックケースは個人と企業(例:学校)の両方に購入されると想定しているため、二峰性分布を使用します。デフォルトのブックケース設定では、個人からの需要が頻繁にあり、顧客1人あたり1〜2台が購入され、これが分布の第一峰を形成します(図4参照)。一方、企業は需要は低頻度ですが、個人以上の大口注文を行うため、企業からの需要が個人の需要に加算されると、分布の第二峰が現れます。この第二峰は右側(高い需要値を示す)にシフトし、発生頻度が低いため第一峰より明らかに小さくなります(図4参照)。また、ペンは個人が購入し、まれに高い需要が発生する(たとえば、試験前に学生が購入する場合など)と仮定しています。さらに、正規分布が 時折 生じることを反映するため、キーボードの売上は正規分布パターンに従います。
Distribution generators(図4参照)内では、操作可能なセルのパラメータを変更することで需要分布を編集できます。例えば、キーボードの平均値(図4内の「NORM parameters」参照)を40から50に引き上げると、分布が10単位右にシフトします。この平均需要の増加により、すべてのキーボード単位 の期待ROIが向上します。同様に、負の二項分布(ペン)および二峰性分布(ブックケース)のパラメータも変更可能です。
Excelはこの種の計算表現力に欠けるため、本デモでは製品ごとの修正を100単位に制限しています。たとえば、キーボードの平均を99に設定すると、Micro purchasing decisions シートで需要単位の約50%が計算に反映されなくなります。
2.2 確率的需要予測の期間設定
通常、予測は日次/週次/月次の区間に分けられますが、これらの離散的な期間は在庫補充の観点からは限定的な有用性しか持ちません。次の lead time 内の需要は、backorders が許可されない限り、今日の購買決定ではカバーできません。なぜなら、購入された単位はリードタイムと同等の期間後に到着するためです。したがって、需要は店舗の現有在庫および発注中在庫(図8参照)でカバーされるべきであり、発注中の単位が需要前に到着することが前提となります。従って、確率的予測は、再発注点間、すなわち Reorder period 1(図9参照)中の需要に関わり、より遠い将来の需要は将来の発注(図9中の Reorder period 2 参照)でカバーされます。

図8. 赤でハイライトされた手元在庫(列F)と発注在庫(列G)は、マイクロ購買判断内に配置されています。リードタイム(列I)は青でハイライトされています。
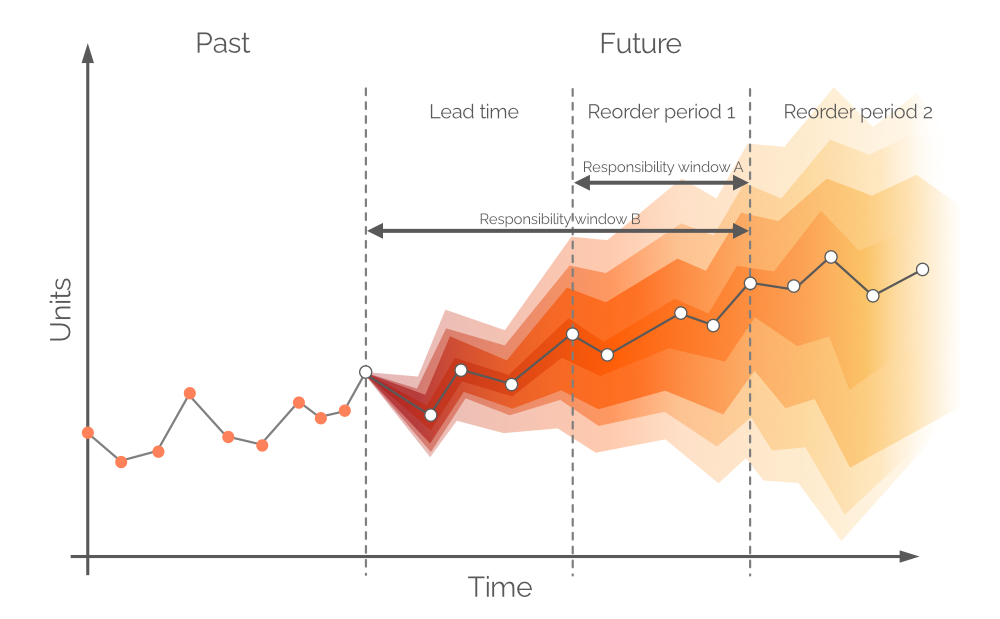
図9. 代替責任ウィンドウの視覚的表現。需要はY軸に、時間はX軸に配置され、左側の点線の縦グレー線が現在の時点(図6に示す「現在」)を示しています。本書の確率的予測は、責任ウィンドウ Bと同等の期間にわたる需要を対象としています。
理論上、確率的需要予測は リオーダー期間1 と同じ期間に基づいて構築されるべきであり、この期間は 責任ウィンドウ A と呼ばれます(図9参照)。これを行うためには、リードタイム終了時点での手元在庫および発注在庫の将来予測を行う必要があります。しかしながら、リードタイム中の需要は(前回の発注期間中に既に意思決定を行ったため)確率的であり、その結果、在庫レベル自体が確率分布となります2。バックオーダーを許容する(一部の業界では一般的な手法です)ことにより、確率的予測は、(リードタイムとリオーダー期間1の)連結期間(図9、別名 責任ウィンドウ B)にわたって構築することが 可能 となります。
リードタイム期間中は、現在の 手元在庫 および 発注在庫 の水準が需要を賄うものと仮定できます。もし品切れが発生した場合、その後の需要はバックオーダーで補われます。これらのバックオーダーは、本日行われたマイクロ購買判断によって対応されます。これにより、手元在庫 および 発注在庫 を、ランダムな値ではなく離散的な値として扱うことが可能となります3.
3. 実行可能な補充判断オプションの特定
実際の在庫補充シナリオでは、確率的予測から各製品ごとに最適な単一の判断(この場合は購入数量)に移行する明確な方法が存在しないため、すべての実行可能な判断オプションを概説する必要があります。単一の 完璧 な選択肢の代わりに、確率的アプローチは、実行可能性 の観点から考慮すべき一連の可能な判断を提示します。
実行可能性 とは、判断が直ちに実行可能であり、追加の計算やチェックなしにそのまま採用できることを意味します。例えば、判断が「実行可能」であるのは、利益が得られ、かつすべての制約(例: 最小発注量 (MOQ)、経済発注量 (EOQ)、ロットサイズ、完全なコンテナ出荷、その他サプライチェーン内の制約)を満たしている場合です4.
マイクロ購買判断 シート(図3および図10)の各行において、特定の製品の発注書に対して在庫を1単位追加することを検討しなければなりません5。この実験の「現在」(または1日目)は、現在の在庫水準を示す行29から始まります。これは、手元在庫と発注在庫の合計として計算されます。もし発注書に1単位を追加することを決定した場合、全体の購入数量は、これまでに購入対象として検討されたすべての単位の合計としてL列で算出されます(図10の注記参照)。
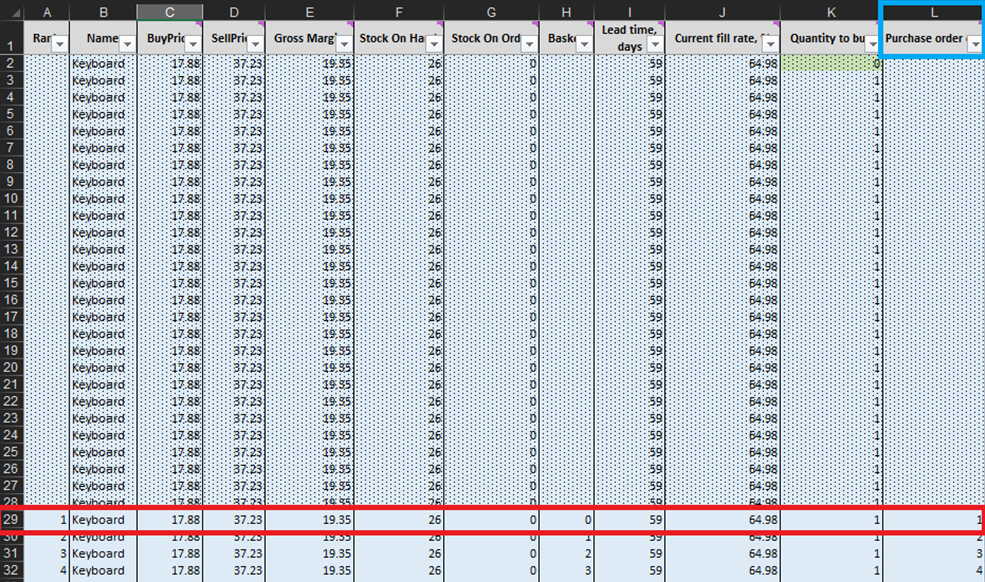
図10. マイクロ購買判断 シート内の表示。赤でハイライトされた行29が、実験開始点(キーボードの場合)です。発注書の列は青でハイライトされています。同じ原則が、行140(ペンの発注の場合)および行240(書棚の発注の場合)にも適用されます。
これらの実行可能な在庫判断が特定されたら、あらゆる購入の経済的報酬を計算し、ランク付けを行います。なお、現在 手元在庫 または 発注在庫 (図10のF列およびG列)に該当する単位に対しては、購入報酬の評価は行いません。既にこれらの単位を購入しているため、理論上の経済的報酬は以前に決定(かつランク付け)されていました。例えば、図10のキーボードデータを見ると、現在在庫は26単位です。したがって、行29から計算を開始し、追加在庫の最初の1単位を発注すべきかどうかを検討します(これにより在庫水準は26単位から27単位に上昇します)。
3.1 実行可能な購買判断の評価
各製品ごとに最適な購入数量を選択するためには、確率的予測で表される不確実な将来を考慮して、各製品のあらゆる実行可能な数量ごとに単位レベルで期待される金銭的リターンを計算する必要があります。これは、在庫意思決定の最も細かいレベルに適用された期待値概念です。
実際には、あらゆる実行可能な判断の期待リターンを計算する際に、あらゆる種類の経済ドライバーを考慮すべきです6。本デモンストレーションの目的のために、以下の要因を考慮します:
- 販売価格: 製品に対して顧客から請求する金額。
- 保管/保管コスト: 製品を保有するための費用。
- 仕入価格: 供給業者または卸売業者から製品を購入する際の費用。
- 品切れ補償: 以下で詳細に説明しますが、あまり知られていないものの重要なドライバーです7.
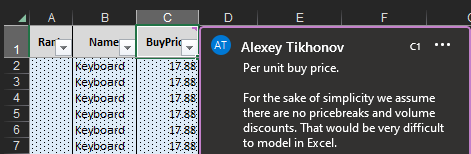
図11. 仕入価格 に関する説明ノート(列ヘッダーにマウスを乗せると表示されます)。Excelドキュメントの各シートには、各列の定義が記載されています。
品切れ補償 は、製品の1単位を在庫として保持するための金銭的インセンティブを表しますが、その目的は 明示的 に販売することではありません。この経済ドライバーは、他の製品に対する相対的な重要度をモデル化するために使用されます。直接的なマージン貢献によって重要性が低いと見なされる製品について、品切れイベントを回避するよう促すインセンティブとなり、これらの製品は間接的に利益率に大きく貢献する可能性があります。このため、むしろ 報酬ドライバー に類似しています8。このドライバーは曖昧なものですが、すべての重要製品(直接的なマージンドライバーでないものも含む)を特定することが極めて重要です。
3.2 各実行可能な判断のスコア計算
在庫補充判断の全体的な経済的結果(すなわち 購入報酬)は、期待マージン、期待在庫コスト および 品切れ補償 など、すべての経済ドライバーの合計です。保管コスト は、在庫補充判断のバランスを取るための逆作用として負のドライバーとして計算に含まれます。
以下は、マイクロ購買判断 シートの行29を例として、各列の数式がもたらす経済的影響の分析です(図12参照)。

図12. Excelシート2の マイクロ購買判断 の行29を使用した、主要な各列ごとのドライバーの内訳。一部の列は図を見やすくするために非表示とされています。
各判断の期待報酬を計算するためには、次のドライバーが必要です:
粗利益 (E列) = 販売価格 – 仕入価格.
販売確率 (Q列) = シート内の数式を参照9.
非販売確率 (列なし) = 100% - 販売確率
期待マージン (R列) = 粗利益 * 販売確率 / 100.
積極性係数 (S列) = 0から1の範囲。このツールでは0.8が選択されています.
品切れ補償 (T列) = 販売価格 * 積極性係数 * 販売確率
保管コスト (U列)
期待在庫コスト (V列) = 保管コスト * 非販売確率10.
以上のデータを使用して、各製品の各単位に対するマイクロレベルの在庫判断の 購入報酬 は以下のように計算されます:
購入報酬 (W列) = 期待マージン + 品切れ補償 + 期待在庫コスト.
購入報酬の見積もりが得られたら、それを用いて後で検討するすべての判断をランク付けするための最終スコアを計算できます。
スコア (Y列) = 購入報酬 / 投資(X列)11.
品切れ補償 は 直接的および間接的 なリターンの両方を含む曖昧なドライバーであるため、購入報酬 は在庫判断の単独での期待リターンを厳密に反映したものではありません。この種のリターンを計算したい場合は、この数式から 品切れ補償 を除外する必要があります12.
4. 実行可能な在庫補充判断のランク付け
各製品ごとのすべての実行可能な在庫購買判断のスコアが得られると、リストが作成され、ランク付けされた購買判断 において降順(高い順から低い順)に並べ替えられます(図13参照)。各実行可能な在庫判断は、正のROI%に基づいて並べ替えられ、各判断には序数順位(第1位、第2位、第3位など)も付与されます(同図のA列参照)。
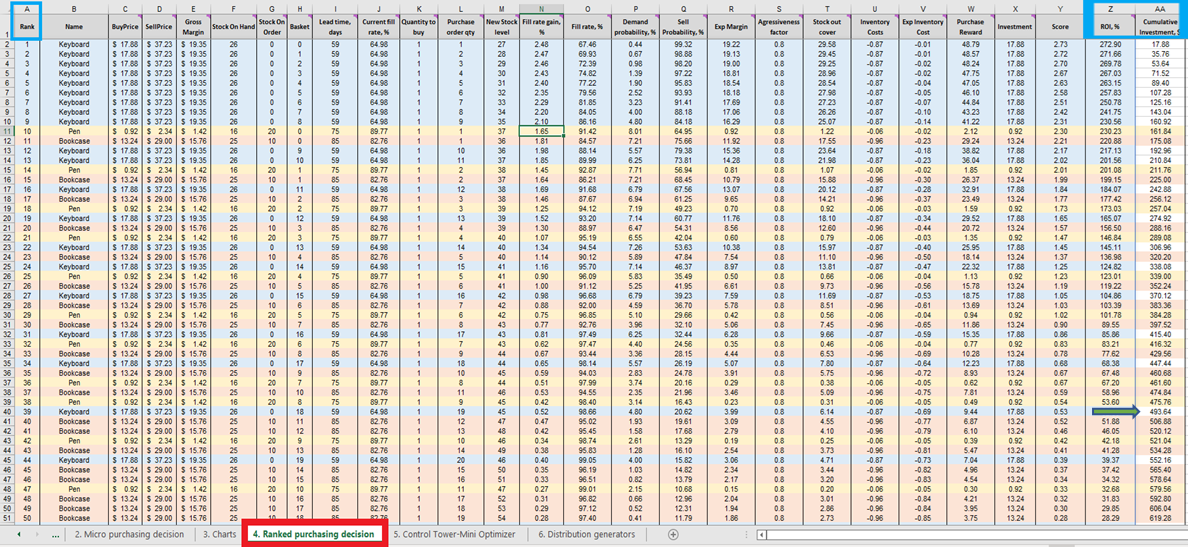
図13. ランク付けされた購買判断 の場所が赤でハイライトされています。A列、Z列、およびAA列は青でハイライトされています。セル40($500予算のカットオフポイント – スプレッドシートのデフォルト)が緑の矢印で示されています。
ランク付けされた購買判断 では、各製品(キーボード、ペン、書棚)ごとに色分けされた行が特徴となっており、ここでは 各製品の1単位の追加 が他のすべての製品の追加単位とどのように相互作用するかを示しています。これらの在庫判断は集合的にROIに影響を与えます。最後に、累積投資 の値が計算されます(図13のAA列)。これは、予算制約に照らして購入判断をどこで終了すべきかを示す指標として使用できますが、これはあくまで1つの終了指標に過ぎません13.
5. 終了基準の決定
終了点を選定する際(ランク付けされた購買判断 においても実際においても)、基準は多くの変数によって異なります。例えば、限られた予算の場合、非常に厳しい利幅のためにROIの最大化が困難になることがあります。また、全体的なサービスレベルの目標があり、その優先順位と利益率の最大化とのバランスを取らなければならない場合も考えられます。
より詳細に言えば、各製品またはカテゴリごとに 異なる サービスレベル目標とともに最大化されたROIを追求するという終了基準を採用することも可能です。したがって、終了基準は企業の包括的なビジネス目標について率直に検討した上で決定されるべき戦略的選択です。優先順位付き在庫補充(PIR)はこの点で非常に柔軟であり、各購買サイクルの終了基準は同じ全体的なランク付け手順を用いて調整可能です。
可能な在庫補充判断を明示的に可視化するために、Charts ダッシュボード(シート3、図14参照)には、各製品ごとに3種類のチャートおよびグラフが用意されています。特に注目すべきは「Driving forces_製品名」であり(図14では キーボード の例が使用されています)、単位レベルで異なる購入数量に応じたROIの推移を示しています。
チャートから明らかなように、購入数量を増加させるとROIが負になるポイントがあります。これは、一定のレベルにおいて、期待在庫コスト の増加により期待マージンが大幅に減少するため、これ以上の単位を購入する意味がなくなるためです。
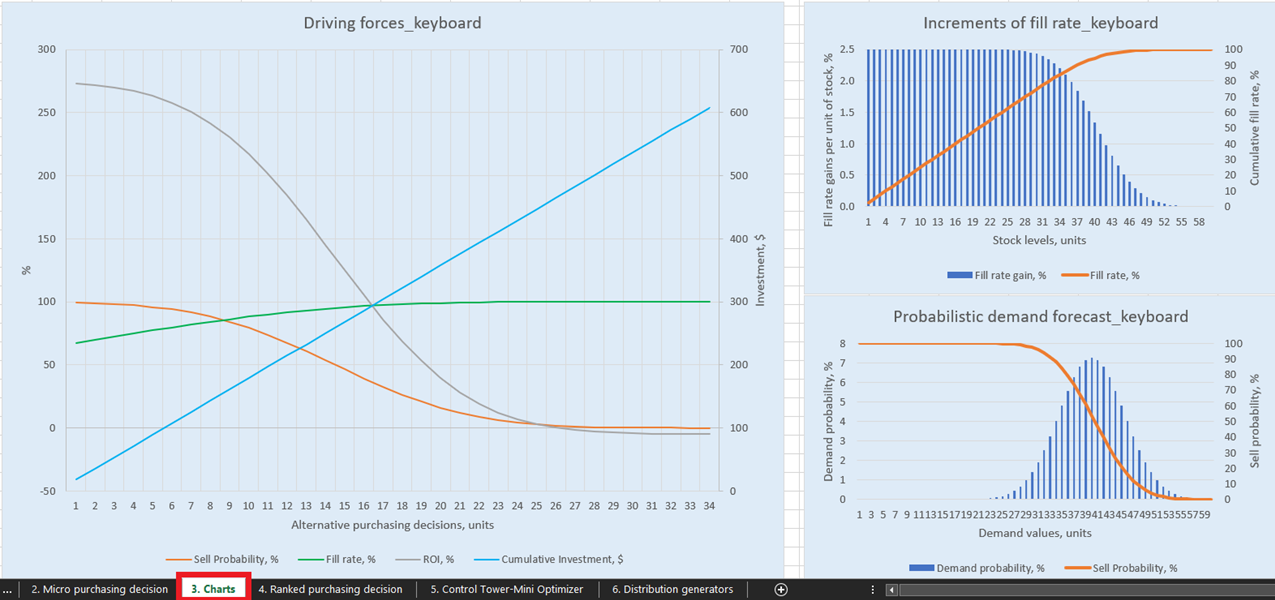
図14. Charts内の「Driving forces_keyboard」の表示。場所は赤でハイライトされています。
終了基準が決定されると、優先順位付き在庫補充判断はSKUごとに集約され、それにより各SKUの 数量、投資額、および Output-Purchase Recommendation において達成された期待フィルレート が更新されます(図15参照)。予算制約($0〜$1450)を変更することで、推奨購入リストも更新されます。便宜上、コントロールタワーには追加で2つのブロック、Base Case – hard copy と Changes to base scenario が設けられています。前者は静的で、Lokadが設計したデモンストレーションのデフォルト設定を表示し、後者はLokadのデフォルト設定と行われた変更との差異を表示します。
コントロールタワー 内の購入推奨リストは、このデモンストレーションの目的を示しています(図15参照)。
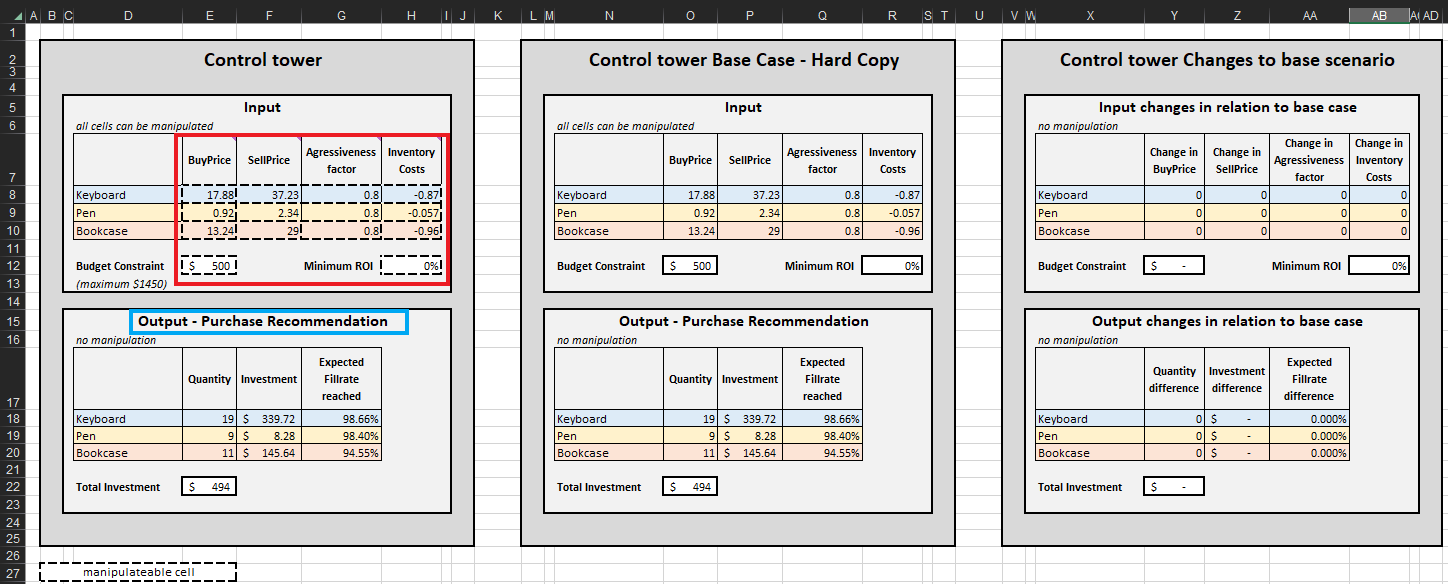
図15. コントロールタワー・ミニオプティマイザーの表示(シート5)。操作可能なセルは赤でハイライトされ、「購入推奨」は青でハイライトされ、優先順位付き在庫補充アプローチの目的を示しています。
6. 結論
従来の時系列予測は、将来の不確実性および制約やドライバーの全体像を反映した在庫補充判断に必要な詳細レベルを捉えることができません。これは、期待される将来の結果に対する確率値で表される明示的な不確実性の次元を欠いているためです。従来の時系列はこの種のデータに実質的に無関心であるため、安全在庫 のような従来の対応策は推測に過ぎず、十分でなければ利益を伴う販売機会(正の期待ROI)が失われ、過剰であればスプレッドシートで示されるように負の期待ROIをもたらす単位を在庫することになってしまいます。
確率的予測を活用した優先的な在庫補充は、この問題に対する我々の解決策です。 このアプローチは、在庫補充の選択肢を個別ではなく_組み合わせ_として考慮します。 その結果、各在庫補充選択肢の期待される財務上のリターンを完全に定量化し、明らかにすることが可能となります。 このアプローチの基礎は、不確実性を受け入れ、確率的予測入力を活用することにあります。 その結果、SKUごとにどのサービスレベルが実質的な財務報酬を生むかをより深く理解でき、恣意的な目標設定を回避することができます。
本書で示すPIR(優先在庫補充)アプローチは、合成データと狭いパラメータを用いて構築されました。 これらの選択は、一般的なツールであるExcelを、一般的でない目的(PIR)に適応させるために行われました。 その他の必要な妥協点として、SKUと単位数は処理時間を短縮するためにそれぞれ3および100に制限されました。なぜなら、全カタログのデータ(ましてや複数店舗のデータ)を処理するのは非常に手間がかかるからです。 さらに、サプライチェーンの制約は加えられていません。 重要な点は、Excelは_確率変数_の処理を目的として設計されていないため、確率的予測とPIRポリシーを生成する上で重要なステップにおいて制限があるということです。 これらの制限は、プロダクショングレードのPIRソリューションには適用されません。
Excelの限界を超えて成長したビジネスを展開するサプライチェーン担当者は、プロダクショングレードのPIRソリューションのデモンストレーションを手配するために、contact@lokad.comへご連絡ください。
7. Overview of the Spreadsheet
7.1 リードミー
このシートは、ユーザー向けのランディングページとして機能します。オンラインチュートリアル(現在お読みのもの)へのリンクが設置されています。
7.2 マイクロ購買意思決定
これは第2シートであり、すべての実行可能な補充意思決定オプションの詳細な財務分析に特化しています。 ここでは_手動によるデータ操作_は行われず、_Control Tower_および_Distribution generators_シートからの入力に基づく計算結果のみが表示されます。
主な特徴:
- 条件付き書式が適用された行は「過去の決定」とみなされ、変更することはできません。 Excelのブラウザ版はフォーマット面で信頼性に欠ける場合があるため、デスクトップアプリの使用を推奨します。
- 各列のヘッダーにカーソルを合わせると、有用な定義や注記が表示されます。
7.3 チャート
これは第3シートで、在庫補充の意思決定に影響を与える主要な要因を視覚化することに特化しています。 ここでは手動によるデータ操作は行われず、このシートは実務者がPIRプロセスの内部動作を視覚化し、より深く理解できるように設計されています。
主な特徴:
- SKUごとに3つのグラフ(キーボード、ペン、ブックケース)。
- 「駆動要因」チャートは、各SKUごとに各意思決定の主要な駆動要因を単位レベルで視覚化します。 そのため、x軸には注文されていないSKUのユニットのみが表示されます。
- 他の2つのチャート(「充足率の増分」と「確率的需要予測」)には、保有在庫と注文可能なユニットを含むすべての在庫が表示されます。
7.4 ランク付けされた購買意思決定
これは第4シートであり、実行可能な補充意思決定をROI/スコアの降順でリスト化することに特化しています。 このリストはシート2(マイクロ購買意思決定)のデータから自動的にソートされ、実行可能な意思決定は互いに関連して表示されます(下記「主な特徴」を参照)。 ここでは手動によるデータ操作は行われず、シート5および6の入力内容の変更に応じてこのリストは変動します。
主な特徴:
- 実行可能な在庫補充意思決定は、ROI/スコアに基づいて降順(高い順から低い順)にランク付けされます。
- ソートされた意思決定に対して累積投資額が計算されます(シート4のカラムAAを参照)。
- 各列のヘッダーにカーソルを合わせると、有用な定義や注記が表示されます。
7.5 コントロールタワー・ミニ最適化ツール
これは第5シートで、モデルの前提(入力)と推奨される意思決定(出力)を要約しています。 操作可能なセル内のデータは変更可能で、それによりモデルの前提および結果が変わります。
主な特徴:
- デモンストレーションを支援するための3つのブロックがあります。1つ目は入力を手動で操作する「Control tower」、2つ目はデフォルト設定を表示する「Base Case – Hard copy」、3つ目は更新後の設定とデフォルト設定の差分を表示する「Changes to base scenario」(シート5参照)。
- 「Control tower」の下に位置する第4のブロック(「Model Assumptions」)は、初期在庫前提の操作に特化しています(シート5参照)。
- 操作可能なセル内のデータのみが変更可能です。
7.6 分布生成器
これは第6シートで、確率的需要予測の生成に特化しています。 操作可能なセル内のパラメータは変更可能で、それにより分布が更新され、新たな確率的需要値が表示されます。
主な特徴:
- SKUごとに1つの分布グラフが表示されます。
- 各SKUにはそれぞれ異なる分布パターンがあり(理由はセクション2.1で説明されています)、
- 分布グラフの一連の左側には、分布のパラメータを操作するためのテーブルがあります。
- 操作可能なセル内のパラメータのみが変更可能です。
- テーブル内の各関連列ヘッダーにカーソルを合わせると、有用な定義や注記が表示されます。
注意事項
-
3つの製品で概念を説明するには十分であり、文書全体を簡潔かつ理解しやすく保つことができます。 ↩︎
-
在庫レベルは、在庫の離散値から確率的需要を差し引くことで確率的になり(離散値から確率分布を引くと別の確率分布が得られます)、Excelでは確率変数を用いた計算を行うのに適していないため、これらすべてを説明するのは非常に複雑になります(「需要確率分布」を考えてください)。 ↩︎
-
これらの妥協は、確率的アプローチの基本原則を示すために必要な措置です。 実際には、バックオーダーは常に使用されるわけではなく、リードタイムは確率的で変動する可能性があります。 ↩︎
-
シンプルさを保つために、サプライチェーンの制約は適用していません。 ↩︎
-
前述のとおり、マイクロ購買意思決定シート内のデータを編集する必要はありません。 すべてのデータ操作はシート5および6を通じて行われます。 ↩︎
-
このExcelシートでは、経済的要因はドルで表現されていますが、通貨自体は重要ではありません。 ↩︎
-
上記の経済的要因のリストは包括的ではなく、実際の在庫補充(およびサプライチェーン)のシナリオでは、ほぼ間違いなくさらに多くの要因が存在します。 これは、商品の生産や腐敗性の制約に直面する場合に特に当てはまります。 ↩︎
-
この要因はB2Cの文脈ではB2Bよりも曖昧です。 後者の場合、欠品イベントに伴う契約上の罰則など明確なペナルティがしばしば存在しますが、前者の場合は欠品イベントの悪影響を金銭的に定量化するのが難しいです。 一般に、SKUの直接的なマージン貢献に関係なく、企業の魅力に不釣り合いな悪影響を及ぼす製品では、この値が高くなります。 前述のように、牛乳はスーパーマーケットにとってマージンドライバーではありませんが、その戦略的な配置(通常は店内の奥)により、顧客は次々と他の高マージン製品が並ぶ通路を歩むことになります。 もしスーパーマーケットでこの主食製品の欠品イベントが発生すると(人々が非常に定期的に、かつまとめ買いする製品)、顧客は店舗を離れ、他店で買い物をし、場合によっては再来店しない可能性があります(これらの欠品イベントが頻発する場合)。 ↩︎
-
売却確率は、Distribution generators(シート6)で生成された確率分布から算出されます。 ↩︎
-
SKUの未販売品を保管し続けることによる継続的なコストです。 ↩︎
-
このシナリオでは、投資額は買付価格と同じですが、これは我々の購買意思決定がMOQやロット倍率に制約されていないためです。 ↩︎
-
これを行う最も簡単な方法は、攻撃性ファクター(図12のS列)をゼロに設定することです。 欠品イベントに悪影響がないと判断した場合に企業が行うかもしれませんが、参考までに申し上げると、実際には必ず悪影響があります。 ↩︎
-
例えば、我々のデフォルト予算は500ドルであり、セル41の値が506.88ドルと予算を超えているため、セル40で購買意思決定を終了します(図13参照)。 その後、製品ごとに数値を集計し、これが購買リスト(図2のControl Towerにおける出力 – 購買推奨)を構成します。 前述のように、設定済みの500ドルの予算は(図2の指示に従い)0ドルから1450ドルの間で任意に編集することができ、これにより異なる予算制約下で購買リストがどのように変化するかを示します。 財務制約に関係なく、ランク付けされた購買意思決定は、ROIの観点から、ランク1から終了点までのすべての行について、最適な在庫意思決定の組み合わせを識別します。 ↩︎