確率的予測（サプライチェーン）

A forecast is said to be probabilistic, instead of deterministic, if it contains a set of probabilities associated with all possible future outcomes, instead of pinpointing one particular outcome as “the” forecast. Probabilistic forecasts are important whenever uncertainty is irreducible, which is nearly always the case whenever complex systems are concerned. For supply chains, probabilistic forecasts are essential to produce robust decisions against uncertain future conditions. In particular, demand and lead time, two key aspects of the supply chain analysis, are both best addressed via probabilistic forecasting. The probabilistic perspective lends itself naturally to the economic prioritization of the decisions based on their expected but uncertain returns. A large variety of statistical models deliver probabilistic forecasts. Some are structurally close to their deterministic counterparts while others are very different. Assessing the accuracy of a probabilistic forecast requires specific metrics, which differ from their deterministic counterparts. The exploitation of probabilistic forecasts requires specialized tooling that diverges from its deterministic counterparts.

決定論的予測 vs. 確率的予測

The optimization of supply chains relies on the proper anticipation of future events. Numerically, these events are anticipated through forecasts, which encompass a large variety of numerical methods used to quantify these future events. From the 1970s onward, the most widely used form of forecast has been the deterministic time-series forecast: a quantity measured over time - for example the demand in units for a product - is projected into the future. The past section of the time-series is the historical data, the future section of the time-series is the forecast.

These time-series forecasts are said to be deterministic because for every point of time in the future, the forecast provides a single value that is expected to match the future outcome as closely as possible. Indeed, while the forecast is single valued, it is widely understood that the forecast has little chance to be perfectly correct. Future outcomes will diverge from the forecast. The adherence of the deterministic forecast to its future outcomes is quantitatively assessed through accuracy metrics, such as the mean square error (MSE) for example.

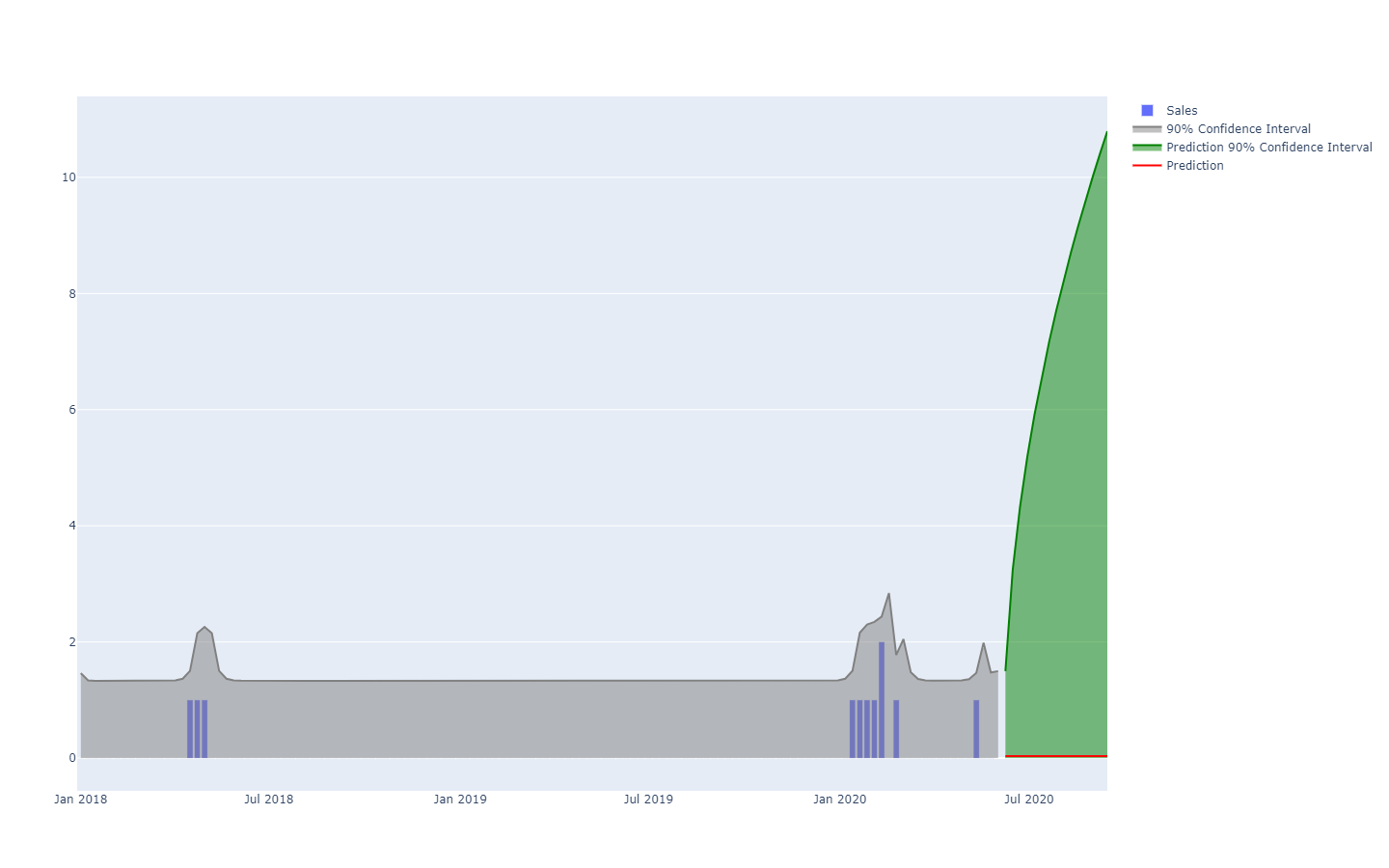
Probabilistic forecasts adopt a different perspective on the anticipation of future outcomes. Instead of producing one value as the “best” outcome, the probabilistic forecast consists of assigning a probability to every possible outcome. In other words, all future events remain possible, they are just not equally probable. Below is the visualization of a probabilistic time-series forecast exhibiting the “shotgun effect”, which is typically observed in most real-world situations. We will be revisiting this visualization in greater details in the following.

Time-series, a quantity measured over time, is probably the most widely-known and most widely-used data model. This data model can be forecast both through deterministic or probabilistic means. However, there are many alternative, typically richer, data models that also lend themselves to forecasts of both kinds. For example, a company that repairs jet engines may wish to anticipate the exact list of spare parts that will be needed for an upcoming maintenance operation. This anticipation can take the form of a forecast, but it won’t be a time-series forecast. The deterministic forecast associated with this operation is the exact list of parts and their quantities. Conversely, the probabilistic forecast is the probability for every combination of parts (quantities included) that this specific combination will be the one needed to perform the repairs.

Also, while the term “forecast” emphasizes an anticipation of some kind, the idea can be generalized to any kind of statistically inferred statement about a system, including for its past (but unknown) properties. The statistical forecasting practice emerged during the 20th century, before the advent of the more modern statistical learning perspective, which encompasses all the data-driven extrapolations that can be performed, irrespective of any temporal dimension. For the sake of clarity, we will keep using the term “forecast” in the following, even if the temporal aspect does always equate past with known and future with unknown. For example, a company may wish to estimate the sales that would have taken place for a product in a store if the product had not been out-of-stock this day. The estimation is useful to quantify the magnitude of the problem in terms of quality of service. However, as the event is past, the “real” sales figure will never be observed. Nevertheless, assuming it has not yet been trivially observed, the statistical estimation of the past demand is a problem that is very close to the estimation of the future demand.

Probabilistic forecasts are richer - information-wise - than their deterministic counterparts. While the deterministic forecast provides a “best guess” of the future outcome, it says nothing about the alternatives. In fact, it is always possible to convert a probabilistic forecast into its deterministic counterpart by taking the mean, the median, the mode, … of the probability distribution. Yet, the opposite does not hold true: it is not possible to recover a probabilistic forecast from a deterministic one.

Yet, while probabilistic forecasts are statistically superior to deterministic forecasts, they remain infrequently used in supply chain. However, their popularity has been steadily increasing over the last decade. Historically, probabilistic forecasts emerged later, as they require significantly more computing resources. Leveraging probabilistic forecasts for supply chain purposes also requires specialized software tools, which are also frequently unavailable.

サプライチェーンの活用事例

Optimizing a supply chain consists of taking the “right” decision - at the present point of time - which will most profitably address a future situation that is only imperfectly estimated. However, the uncertainty associated with future events is irreducible to a large extent. Thus, the company needs the decision to be robust if the anticipation of the future event - i.e. the forecast - is imperfect. This has been done minimally since the mid 20th century through the safety stock analysis. However, as we will see below, beside historical interest, there is no longer any reason to favor safety stocks over “native” probabilistic numerical recipes.

The probabilistic forecasting perspective takes a radical stance towards uncertainty: this approach attempts to quantify the uncertainty to the greatest extent. In supply chain, costs tend to be concentrated on the statistical extremes: it’s the unexpectedly high demand that creates the stockout, it’s the unexpectedly low demand that creates the inventory write-off. In between, the inventory rotates just fine. Probabilistic forecasts are - crudely put - an attempt at managing these low-frequency, high-cost situations that are ubiquitous in modern supply chains. Probabilistic forecasts can and should be seen as a core ingredient of any risk management practice within the supply chain.

Many aspects of supply chains are particularly suitable for probabilistic forecasting, such as:

• 需要: 衣料品、アクセサリー、スペアパーツなど、多くの製品は不規則または断続的な需要と関連しています。製品の発売は成功する場合もあれば失敗する場合もあります。競合他社のプロモーションは、市場シェアの大部分を一時的かつ不規則に奪うことがあります.
• リードタイム: 海外からの輸入では、生産、輸送、通関、受け取りなど、チェーンのあらゆる段階で一連の遅延が発生する可能性があります。地元のサプライヤーであっても、在庫切れに直面すれば稀に長いリードタイムが発生することがあります。リードタイムは「ファットテール」分布を示す傾向があります.
• 歩留まり（生鮮食品）: 多くの生鮮食品の生産量と品質は、企業が制御できない天候などの条件に依存します。確率的予測はこれらの要因をシーズン全体で定量化し、従来の天気予報の枠を超える見通しを提供します.
• 返品（eコマース）: 顧客が同じ製品を3サイズで注文した場合、そのうち2サイズが返品される可能性が高いです。一般的に地域間で大きな違いはあるものの、顧客は有利な返品ポリシーが存在するとその恩恵を受ける傾向があります。各注文に対する返品の確率は評価されるべきです.
• スクラップ（航空分野）: 修理可能な航空機部品（しばしばロタブルと呼ばれる）は、修理に失敗する場合があります。この場合、その部品は航空機に再搭載するには適さないため廃棄されます。部品が修理後に生存するか否かを事前に知ることは通常不可能ですが、スクラップとなる確率は推定されるべきです.
• 在庫（B2C小売）: 顧客は小売店から商品をずらしたり、損傷させたり、さらには盗んだりする可能性があります。したがって、電子的な在庫レベルは、顧客が認識する実際の棚上の在庫状況の概算に過ぎません。顧客が認識する在庫レベルは、確率的予測によって推定されるべきです.
• …

This short list illustrates that the angles eligible for a probabilistic forecast vastly exceed the sole traditional, “demand forecasting” angles. The well-engineered optimization of a supply chain requires to factor all the relevant sources of uncertainty. While it is sometimes possible to reduce the uncertainty - as emphasized by lean manufacturing - there are usually economic trade-offs involved, and as a result, some amount of uncertainty remains irreducible.

Forecasts, however, are merely educated opinions about the future. While probabilistic forecasts may be considered as remarkably fine-grained opinions, they are not fundamentally different from their deterministic counterparts in this regard. The value, supply chain wise, of the probabilistic forecasts is found in the way that this fine structure is exploited to deliver more profitable decisions. In particular, probabilistic forecasts are typically not expected to be more accurate than their deterministic counterparts if deterministic accuracy metrics are used to assess the quality of the forecasts.

変動性の擁護

Despite what many approaches to supply chain advocate, variability is here to stay - hence the need for probabilistic forecasts. The first misconception is that variability is necessarily a bad thing for a supply chain; it isn’t. The second misconception is that variability can be engineered away; it can’t.

Variability has positive implications for supply chains in multiple situations. For example, on the demand side, most verticals are driven by novelty, such as fashion, cultural products, soft and hard luxury - as are “hit or miss” businesses. Most new products aren’t successes (misses), but the ones that succeed (hits) yield massive returns. Extra variability is good because it increases the probability of outsized returns, while downsides remain capped (worst case, the whole inventory is written off). The neverending stream of new products pushed to market ensures the constant renewal of “hits”, while the old ones are waning.

On the supply side, a sourcing process that ensures highly variable pricing offers is superior - all things considered equal - to an alternative process that generates much more consistent (i.e. less variable) prices. Indeed, the lowest priced option is selected while the others are dismissed. It does not matter whether the “average” sourced price is low, what matters is uncovering lower priced sources. Thus, the good sourcing process should be engineered to increase variability, for example by emphasizing the routine exploration of new suppliers as opposed to restricting the sourcing process to the well-established ones.

Sometimes, variability may be beneficial for more subtle reasons. For example, if a brand is too predictable when it comes to its promotional operations, customers identify the pattern and start delaying their purchase as they know that a promotion is coming and when. Variability - erraticity even - of the promotional activities mitigates this behavior to some extent.

Another example is the presence of confusion factors within the supply chain itself. If new products are always launched with both a TV campaign and a radio campaign, it becomes statistically difficult to distinguish the respective impacts of the TV and of the radio. Adding variability to the respective campaign intensity depending on the channel ensures that more statistical information can be extracted from those operations afterward, which can be later on turned into insights for a better allocation of the marketing resources.

当然ながら、すべての変動が良いというわけではありません。リーン生産方式は、サプライチェーンの生産側において、変動が通常有害である、とりわけ遅延のばらつきに関しては特にそうであると強調しています。実際、LIFO（後入れ先出し）方式が偶然混入し、その結果、リードタイムのばらつきがさらに悪化することがあります。そのような状況では、偶発的な変動は、通常、より良いプロセスあるいは場合によってはより良い設備や施設によって取り除かれるべきです。

変動は、有害である場合でもしばしば本質的に低減不可能です。以下のセクションで見ていくように、サプライチェーンは小さな数の法則に従います。決定論的視点から店舗レベルを信頼性高く予測できると考えるのは幻想であり、実際、顧客自身も何を購入するか正確には分かっていません。より一般的には、変動の低減には常にコストが伴い（さらに低減すればなおさらコストがかかる）、変動の限界的な低減は収穫逓減に終始するため、経済的な要因から、変動を低減できたとしても完全に排除することはほとんど不可能です。

小さな数の法則

サプライチェーンにおける小さな数の法則は、「小さな数がチェーン全体に支配的である」と表現できます。この観察則は、規模の経済や、サプライチェーンの多くの構造的側面を駆動するその他の要因によって生じます:

• 一日あたり数万単位の材料を供給するサプライヤーは、発注を頻繁に行わせないための最小発注数量（MOQ）や価格優遇措置が設定されている可能性が高いです。結果として、あるサプライヤーに対して一日に発行される発注の数は、一桁に留まることがほとんどです。
• 一日あたり数万単位を生産する工場は、数千単位の大ロットでの運用を行っている可能性が高いです。生産された製品はパレット単位で梱包されることが一般的で、ある日のバッチ数はせいぜい二桁の小さな数にとどまります。
• 一日あたり数万単位を受け取る倉庫には、トラックによる納品が行われ、各トラックは貨物全体を一度に降ろします。非常に大きな倉庫であっても、一日のトラック納品の回数は二桁を超えることはほとんどありません。
• 数万単位の在庫を持つ小売店は、数千種類にも及ぶ異なる製品ラインナップを展開している可能性が高く、各製品ごとに保持される在庫数が一桁を超えることは非常に稀です。
• …

当然ながら、単位を変更すれば数値を大きく見せることは可能です。たとえば、パレットの数を数える代わりにパレットの_グラム_数や、米ドルのセント単位の金額を数えれば、大きな数字が現れます。しかし、小さな数の法則は、物事を合理的なサプライチェーンの視点で数えるという考え方の下で理解されるべきです。理論上はこの原則がかなり主観的に見えるかもしれませんが、近代サプライチェーンの明白な離散的実態（バンドル、箱、パレット、コンテナ、トラック…）によって、実際にはそうではありません。

この法則は、確率的予測の視点において非常に重要です。まず、サプライチェーンの状況では 離散的 な予測が支配的であり、予測（または決定）される結果は分数ではなく整数であることを示しています。確率的予測は、各離散的結果に対して確率を推定できるため、特に離散的な状況に適しています。これに対し、決定論的予測は離散的な結果の扱いに苦労します。たとえば、ある製品の日次売上が1.3単位で予測されるというのはどういう意味でしょうか？単位は分割して販売されるものではありません。この記述からはより合理的な「離散的」解釈が導かれるかもしれませんが、確率的対応、たとえば「需要が0単位となる確率27%、1単位が35%、2単位が23%…」という表現は、対象現象の離散性をそのまま受け入れており、はるかに明快です。

第二に、確率的予測は生の計算リソースという点で劇的に困難に見えるかもしれませんが、実際には小さな数の法則によりそうではありません。実際、前述の日次製品売上に戻ると、ある日需要が100を超える確率を数値で評価する意味はほとんどありません。これらの確率はゼロ、もしくは非常に僅かな任意の値に丸められ、その結果、サプライチェーンモデルの数値精度への影響は無視できるものとなります。一般的な目安として、確率的予測は決定論的予測に比べて約3桁分の計算リソースを必要とすると考えられます。しかし、このオーバーヘッドにもかかわらず、サプライチェーンパフォーマンステストの面から見れば、その利点は計算リソースのコストを大きく上回ります。

確率的予測の精度指標

いかなる状況でも、十分に設計された確率的予測は、この結果が発生する非ゼロの確率が実際に存在したことを示しています。一見すると、確率的予測があたかも現実から独立しているかのように思えるかもしれません―まるで未来予知者が、後になってその予言の正しい解釈方法を取り繕うかのようですが。しかし実際には、確率的予測の品質を定量的に評価する方法は多数存在します。その中には、決定論的予測の精度評価に使われる指標に似た_メトリクス_もあれば、決定論的視点とは一線を画す、より急進的で深遠な評価方法もあります。

ここでは、確率的予測の精度を評価するための4つの異なるアプローチを簡単に見ていきましょう:

• ピンボール損失関数
• 連続ランク付け確率スコア（CRPS）
• ベイジアン尤度
• 生成的敵対的視点

ピンボール損失関数は、確率的予測から導かれる分位点推定の精度指標を提供します。例えば、特定の製品について店舗の顧客需要を98%以上満たす在庫量を評価したい場合、この数量は需要が0単位、1単位…と確率を足し合わせ、初めて98%を超える地点で直接確率的予測から得ることができます。ピンボール損失関数は、この将来需要の偏った推定値の品質を直接測定する手段として機能し、確率的予測の累積密度関数の任意の点の品質評価ツールと見なすことができます。

連続ランク付け確率スコア（CRPS）は、観測された結果に全確率質量を移動させるために必要な「変位量」として解釈できる指標を提供します。これは、平均絶対誤差（MAE）の確率的視点への最も直接的な一般化であり、CRPSの値は結果そのものの単位と一致します。この視点は、「輸送理論」やモンジュ・カントロヴィッチ距離と呼ばれる手法を通じて、一次元に限らず任意の計量空間へと一般化することが可能ですが、これは本書の範囲を超えます。

尤度およびそのクロスエントロピーの類似物は、最小の驚き度 というベイジアン的視点を採用します。つまり、観測された結果の確率が高ければ高いほど良いという考え方です。例えば、確率的モデルAとBがあり、モデルAはある日需要が0単位となる確率を50%とし、モデルBは同じ条件で1%と主張するとします。3日間の観測結果が0, 0, 1であった場合、モデルAでは約10%の確率でこれらの結果が得られたのに対し、モデルBではおよそ0.01%に過ぎません。したがって、モデルBが正しいモデルである可能性は、モデルAに比べてはるかに低いのです。尤度は、意味のある_絶対的_な基準をもってモデルを評価する決定論的視点からは逸脱し、あくまでモデルの_比較_のための手段を提供しますが、数値的には比較以外の用途にはほとんど使えないという側面があります。

生成的敵対的視点は、この問題に対する最も現代的なアプローチです（Ian Goodfellow et al., 2014）。本質的には、この視点は、「最良」の確率的モデルとは、モンテカルロ方式で生成された結果が実際の結果と区別がつかないものであるモデルであると述べています。例えば、ある地域の大型スーパーマーケットにおける歴史的な取引記録を考え、過去の任意の時点でその記録を切り詰め、以降、確率的モデルを用いて偽ながらも現実的な取引を生成したとします。統計解析によって、データセットが「現実」から「偽」へと切り替わる時点が特定できなければ、そのモデルは「完璧」と見なされるでしょう。生成的敵対的アプローチの要旨は、あらゆる確率的モデルの欠陥を浮き彫りにする指標を「学習」することにあります。特定の指標に依存するのではなく、この視点は機械学習技術を再帰的に利用して、指標そのものを「学習」していきます。

確率的予測の品質にアクセスするより良い方法を模索することは、依然として活発な研究分野です。『より良い予測をどのように作るか？』と『予測がより良いかどうかをどのように判断するか？』という二つの問いの間に明確な境界はなく、近年の研究成果によりその境界は大幅に曖昧になっています。次なる突破口は、確率的予測が捉えられる方法自体の更なる変革を伴う可能性が高いでしょう。

極めて小さな確率と対数尤度

多次元の状況を確率的予測の視点から見ると、極めて小さな確率が自然に生じます。これらの小さな確率は、コンピュータが無限の精度で数値を処理できないため、厄介な問題となります。生の確率値は、数値精度の制限により「極めて」小さく、ゼロに丸められてしまうことがよくあります。この問題の解決策は、計算リソースの観点から非常に非効率な任意精度計算ソフトウェアにアップグレードすることではなく、乗算を加算法に変換する「対数トリック」を使用することです。この手法は、確率的予測を扱うほぼすべてのソフトウェアで何らかの形で活用されています。

ここでは、ある店舗で提供される$$n$$種類の異なる製品について、その日の需要を表す確率変数$$X_1, X_2, \ldots, X_n$$が存在すると仮定します。各製品について、日末に観測される実際の需要を$$\hat{x}_1, \hat{x}_2, \ldots, \hat{x}_n$$とします。最初の製品（$$X_1$$で表される）について、$$\hat{x}_1$$が観測される確率は$$P(X_1=\hat{x}_1)$$と書かれます。 . さて、わかりやすくするため、多少無理やりですが、すべての製品の需要が完全に独立であると仮定しましょう。$$\hat{x}_1, \hat{x}_2, \ldots, \hat{x}_n$$が同時に観測される確率は、

もし$$P(X_k=\hat{x}_k) \approx \tfrac{1}{2}$$（大雑把な近似）で、かつ$$n=10000$$であれば、上記の同時確率は$$\tfrac{1}{{2^{10000}}} \approx 5 \times 10^{-3011}$$程度となり、非常に小さな値となります。この値は、64ビット浮動小数点数など、科学計算で一般的に使用される数値表現の限界を下回ってしまいます。

「対数トリック」とは、式の対数を用いる方法、すなわち、

対数を取ることで、乗算の連続が加算の連続に変換され、これにより乗算の連続よりもはるかに数値的に安定した計算が可能となります。

確率的予測が関与する場合、常に「対数トリック」が使用されます。_対数尤度_とは、まさに（前述の）尤度の対数であり、生の尤度は一般的な浮動小数点数では数値的に表現不可能であるためです。

確率的予測のアルゴリズム的アプローチ

確率的予測のコンピュータによる生成の問題は、機械学習そのものの分野と同じくらい広大です。これら二つの分野の境界が存在するとしても、それは主に主観的な選択の問題です。それにもかかわらず、このセクションでは、確率的予測を得るために利用できる注目すべきアルゴリズム的アプローチの、選択的なリストを示します。

20世紀初頭、あるいは19世紀後半に、需要の不確実性を正規分布に基づいてモデル化するという考えに基づく安全在庫の概念が登場しました。他の科学分野、特に物理学ではすでに正規分布の事前計算済みの表が確立されていたため、安全在庫の適用は、既存の表から引き出された「安全在庫」係数と需要レベルの乗算を行うだけで済みました。逸話的には、1990年代までに書かれた多くのサプライチェーンの教科書には、付録に正規分布の表が掲載されていました。しかし、このアプローチの主な欠点は、正規分布がサプライチェーンにおいて合理的な前提ではないという点にあります。まず、サプライチェーンに関しては、_何も_が_通常_分布するとは言えません。次に、正規分布は連続分布であり、サプライチェーンイベントの離散的な性質（上記「小さな数の法則」を参照）と矛盾します。したがって、技術的には「安全在庫」には確率的要素があるものの、その根底にある方法論や数値レシピは、決定論的視点に基づいています。本書では、明確化のためにこのアプローチを列挙しています。

2000年代初頭に話を進めると、アンサンブル学習法 ― その代表例としてはおそらくランダムフォレストや勾配ブースティングツリーが挙げられる ― は、その決定論的な起源から確率論的な視点へと拡張するのが比較的容易になりました。アンサンブル学習の基本的な考え方は、決定木などの弱い決定論的予測器を多数組み合わせ、より優れた決定論的予測器を作ることにあります。しかし、混合のプロセスを調整して単一の集約値ではなく確率を得ることが可能であり、結果としてアンサンブル学習法は確率論的な 予測方法 へと転換されます。これらの手法はノンパラメトリックであり、サプライチェーンで一般的に見られる裾の重い分布や多峰性分布に適合する能力を持っています。これらの手法には2つの顕著な欠点があります。まず、構造上、このクラスのモデルが生成する確率密度関数は多くのゼロを含む傾向があり、そのため対数尤度指標を活用する試みが妨げられます。より一般的には、これらのモデルはベイズ的視点に合致せず、新たな観測がしばしば「不可能」（すなわちゼロ確率）と宣言されるためです。しかし、この問題は正則化手法によって解決可能です¹。第二に、モデルは入力データセットのかなりの部分と同等の大きさになる傾向があり、「予測」操作は「学習」操作とほぼ同程度の計算コストを要します。

2010年代に爆発的に台頭した「ディープラーニング」と総称されるハイパーパラメトリック手法は、ほぼ 偶然にも 確率論的な性質を持っていました。実際、ディープラーニングが真価を発揮するタスク（例えば画像分類など）では決定論的予測にのみ焦点が当てられる一方で、上記で述べた対数尤度の変種であるクロスエントロピー指標は非常に急峻な勾配を示し、確率的勾配降下法（SGD）に非常によく適合することが判明しました。したがって、ディープラーニングモデルが確率論的に設計されるのは、確率そのものに関心があったからではなく、損失関数が確率論的予測を反映することで勾配降下が速く収束するためです。このように、ディープラーニングに関しては、他の多くのユースケースが確率分布を平均、中央値または最頻値に単純に集約するのに対し、サプライチェーンはディープラーニングモデルの実際の確率論的出力に関心を示しているのが特徴です。Mixture Density Networksは、複雑な確率分布の学習を目指したディープラーニングネットワークの一種です。その結果はパラメトリックな分布であり、おそらくガウス分布の組み合わせで構成されます。しかし、セーフティストックとは異なり、複数のガウス分布の混合は実際にはサプライチェーンで観察される裾の重い挙動を反映する可能性があります。ディープラーニング手法は最先端とみなされることが多いものの、特に密度混合が関与する場合に数値的安定性を達成することは、いまだに「暗黒の技術」ともいえる側面があります。

微分可能プログラミングは、2010年代後半に人気を博したディープラーニングの子孫です。技術的な属性の多くをディープラーニングと共有していますが、焦点は大きく異なります。ディープラーニングが多数の単純な関数（例：畳み込み層）を積み重ねることで任意の複雑な関数（例：囲碁のプレイなど）を学習することに注力するのに対し、微分可能プログラミングは学習プロセスの細部構造に焦点を当てています。最も細かく、表現力豊かな構造は、文字通りプログラムとして形式化でき、そこには分岐、ループ、関数呼び出しなどが含まれます。微分可能プログラミングは、問題が高度に構造化された形で現れ、その構造が専門家に知られているため²、サプライチェーン分野で非常に注目されています。例えば、あるシャツの販売は別の色のシャツによって食い合わされることはあっても、サイズが3違うシャツの販売によっては食い合わされません。このような構造的事前知識は高いデータ効率を実現する鍵となります。実際、サプライチェーンの観点ではデータ量が非常に限られている（小さい数の法則を参照）ため、問題を構造的に「枠組み化」することで、限られたデータ下でも望ましい統計パターンが学習されることが保証されます。さらに、構造的事前知識は数値的安定性の問題にも対処するのに役立ちます。一方、アンサンブル手法と比較すると、構造的事前知識は特徴量エンジニアリングに比べて手間がかからず、モデルの保守も簡素化されるのです。ただし、微分可能プログラミングは今日に至るまでまだかなり新しいアプローチと言えます。

モンテカルロの視点（1930年代～1940年代）は、確率論的予測に別の角度からアプローチするために利用できます。これまでに議論されたモデルは明示的な確率密度関数（PDF）を提供しています。しかし、モンテカルロの視点からは、モデルは生成器、すなわちサンプラーに置き換えられ、可能な結果（時に「偏差」とも呼ばれる）をランダムに生成します。生成器の結果を平均することでPDFが再構築されますが、計算資源の要求を削減するためにPDF自体を省略することもよくあります。実際、生成器はそれが表現するPDFに比べ、データ面で非常にコンパクトになるよう設計されることが多いのです。確率論的予測に直接取り組むために挙げた多くの機械学習手法は、生成器の学習に寄与することができます。生成器は、低次元のパラメトリックモデル（例：状態空間モデル）やハイパーパラメトリックモデル（例：ディープラーニングにおけるLSTMやGRUモデル）の形を取ることができます。アンサンブル手法は、その「予測」操作にかかる計算コストが高いため、生成プロセスを支援するために用いられることはほとんどありません。

確率論的予測の取り扱い

確率論的予測から有用な洞察や意思決定を導き出すには、専用の数値ツールが必要です。決定論的予測では数値そのものが示されるのに対し、確率論的予測は明示的な確率密度関数またはモンテカルロ生成器として表現されます。実際、確率論的ツールの品質は、確率論的予測自体の品質と同じくらい重要です。このツールがなければ、確率論的予測の活用は決定論的プロセスに陥ってしまいます（詳細は下記の「アンチパターン」セクションを参照）。

例えば、ツールは以下のようなタスクを実行できなければなりません：

• 不確実な生産リードタイムと不確実な輸送リードタイムを組み合わせ、「全体の」不確実なリードタイムを算出する。
• 不確実な需要と不確実なリードタイムを組み合わせ、発注予定の在庫でカバーすべき「全体の」不確実な需要を算出する。
• 不確実な注文返品（eコマース）と、輸送中のサプライヤー注文の不確実な到着日を組み合わせ、不確実な顧客リードタイムを算出する。
• 統計的手法で作成された需要予測に、パンデミックのように履歴データに反映されない高次の文脈から手動で導出されたテールリスクを補完する。
• 不確実な需要と、賞味期限に関する在庫の不確実な状態（食品小売）を組み合わせ、日終了時の不確実な在庫残量を算出する。
• …

すべての確率論的予測 ― 需要予測に限らず ― が適切に組み合わされれば、サプライチェーンの意思決定の最適化が行われるべきです。これは、制約条件およびスコア関数に対して確率論的な視点を取り入れることを意味します。しかし、このツールに関する詳細は本書の範囲外です。

確率論的予測に取り組むためのツールは大きく2種類に分けられます。1つは確率変数に関する代数であり、もう1つは確率プログラミングです。これらの2つの手法は、それぞれ利点と欠点が異なるため、相互に補完し合います。

確率変数の代数は通常、明示的な確率密度関数を対象とします。この代数は、加算、減算、乗算などの通常の算術演算を、確率論的な対応物に置き換えて扱い、しばしば確率変数を統計的に独立であると仮定します。この代数は、単なる数値で表される決定論的手法に匹敵する数値的安定性を提供します。さらに、すべての中間結果を後で利用するために保持できるため、データ抽出パイプラインの整理やトラブルシューティングに非常に役立ちます。一方で、これらの代数の表現力は限定的であり、確率変数間に存在する微妙な条件付き依存関係すべてを表現することは通常不可能です。

確率プログラミングは、モンテカルロの視点を問題に適用します。論理は一度記述され、通常は完全に決定論的な視点に基づいていますが、目的の統計を収集するためにツール（すなわちモンテカルロプロセス）を通じて何度も実行されます。最大限の表現力は「プログラム的」な構造によって達成され、確率変数間の任意かつ複雑な依存関係をモデル化することが可能です。確率プログラミングによる論理の記述は、単なる数値のみを扱うため、確率変数の代数と比べるとやや容易である傾向にあります。一方で、数値的安定性（反復回数が増えるほど精度が向上する）と計算資源（反復回数の増加はコストの増大を招く）との間には常にトレードオフがあります。さらに、中間結果は計算資源への負担を軽減するため、一時的なものとしてしか存在しないため、容易にアクセスすることはできません。

近年のディープラーニングの研究は、上述の2つの手法以外にもさらなるアプローチが存在することを示唆しています。例えば、変分オートエンコーダーは、潜在空間 上での操作を行う視点を提供し、データに対して非常に複雑な変換を追求しながらも印象的な成果を上げています（例：写真のポートレートから自動的に眼鏡を除去する）。これらの手法は概念的には非常に興味深いものの、サプライチェーン問題に取り組む上では現時点であまり実用的な関連性を示していません。

確率論的予測の可視化

離散的な確率分布を可視化する最も簡単な方法はヒストグラムであり、縦軸は確率、横軸は対象となる確率変数の値を示します。例えば、リードタイムの確率論的予測は次のように表示できます：

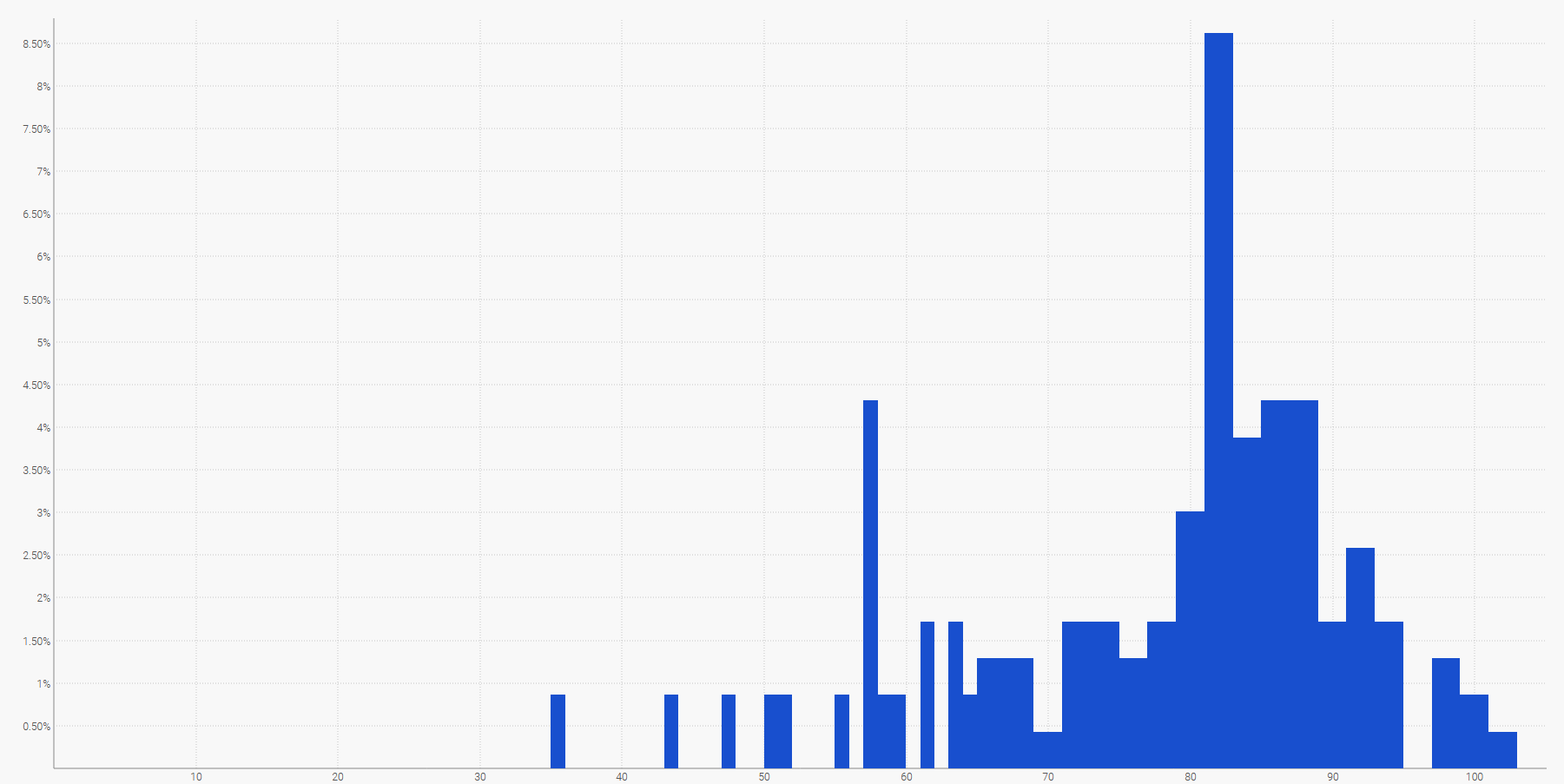
特定の期間にわたって合計された将来の需要もまたヒストグラムで表現することができます。より一般的には、ヒストグラムは相対整数の集合である $${ℤ}$$ 上のすべての一次元確率変数に適しています。

等間隔の時系列、すなわち等しい長さの離散的な時間期間にわたって変動する量の確率論的同等物の可視化は、既に非常に困難です。実際、一次元の確率変数とは異なり、そのような分布の標準的な可視化方法は存在しません。期間が互いに独立であると仮定できないことに注意してください。したがって、各期間ごとに1つずつヒストグラムを並べて「確率論的」時系列を表現することは可能ですが、この表現はサプライチェーンにおける事象の展開の仕方を著しく誤って伝えることになります。

例えば、新たに発売された製品が好調に推移し、高い売上高（ヒット）を記録する可能性はそれほど低くはありません。同様に、同じ新製品が失敗して低い売上高（ミス）に終わる可能性もそれほど低くはありません。しかし、ヒットとミスの間で日々大幅な変動が生じることは極めて考えにくいです。

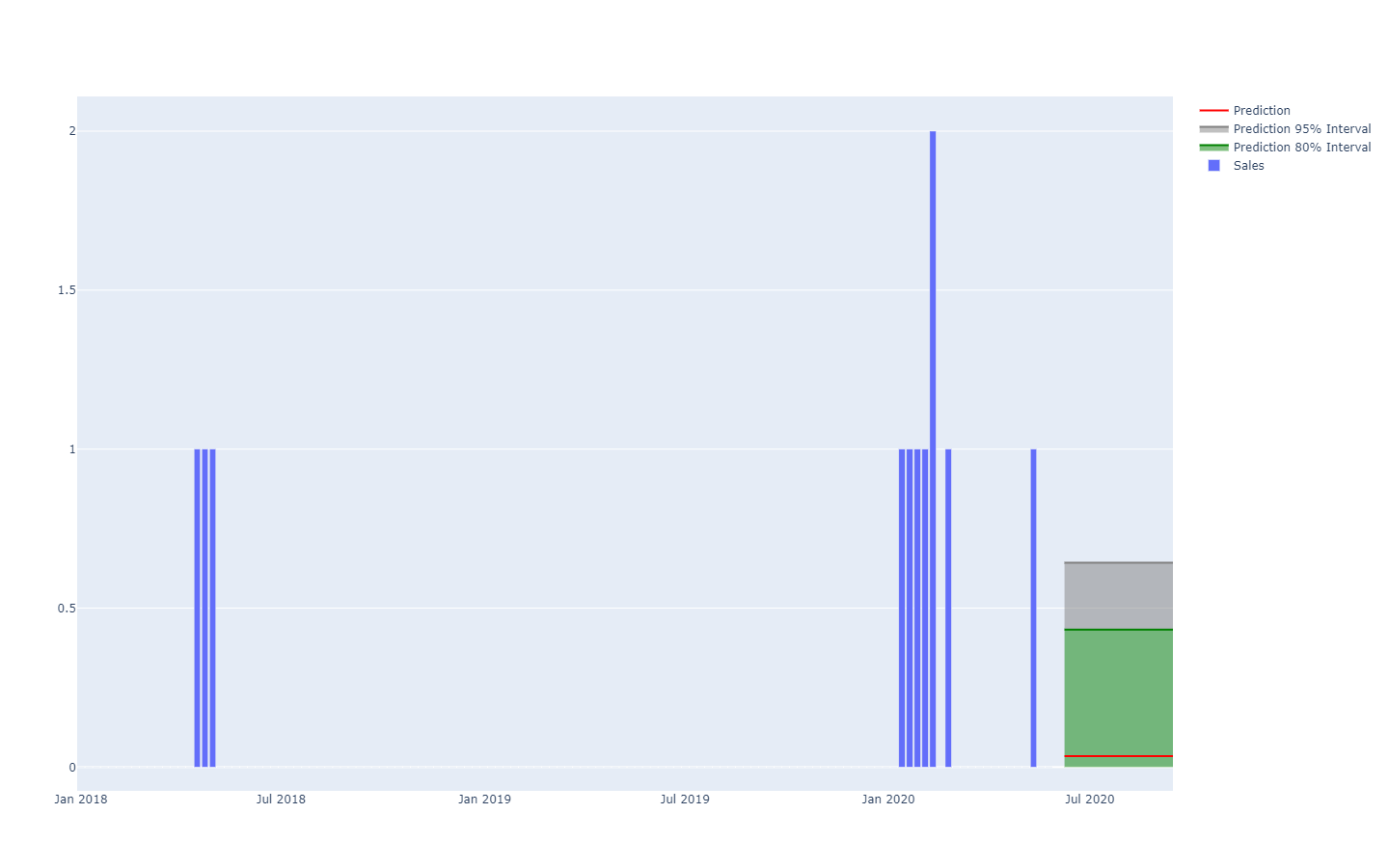
サプライチェーン文献で一般的に見られる予測区間は、やや誤解を招く恐れがあります。これらは実際のサプライチェーン状況を代表しない、不確実性の低い状況を強調しがちです；

これらの予測区間が、特定の分位点しきい値を示すための配色スキームと並べられた確率分布そのものであることに注目してください。

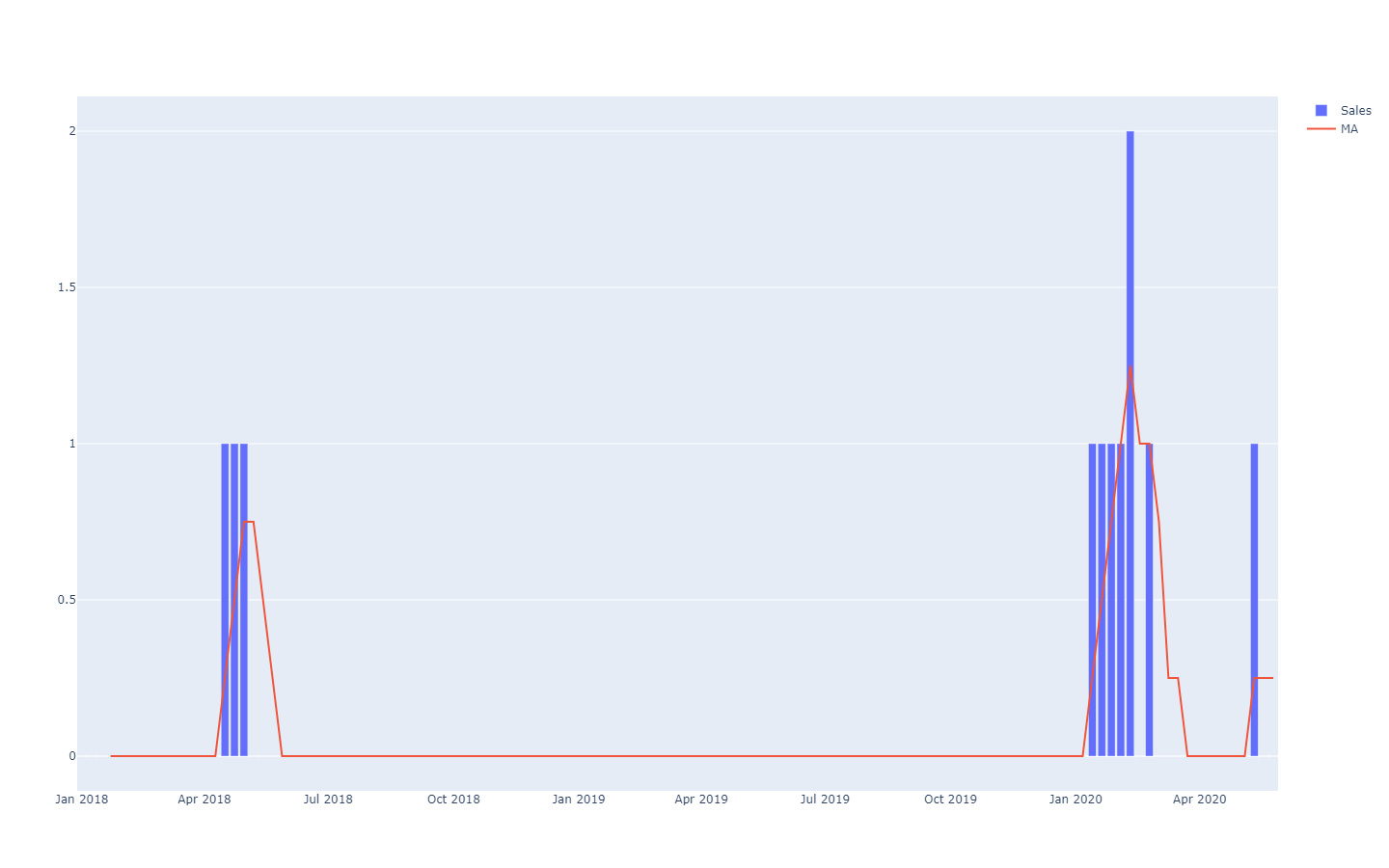
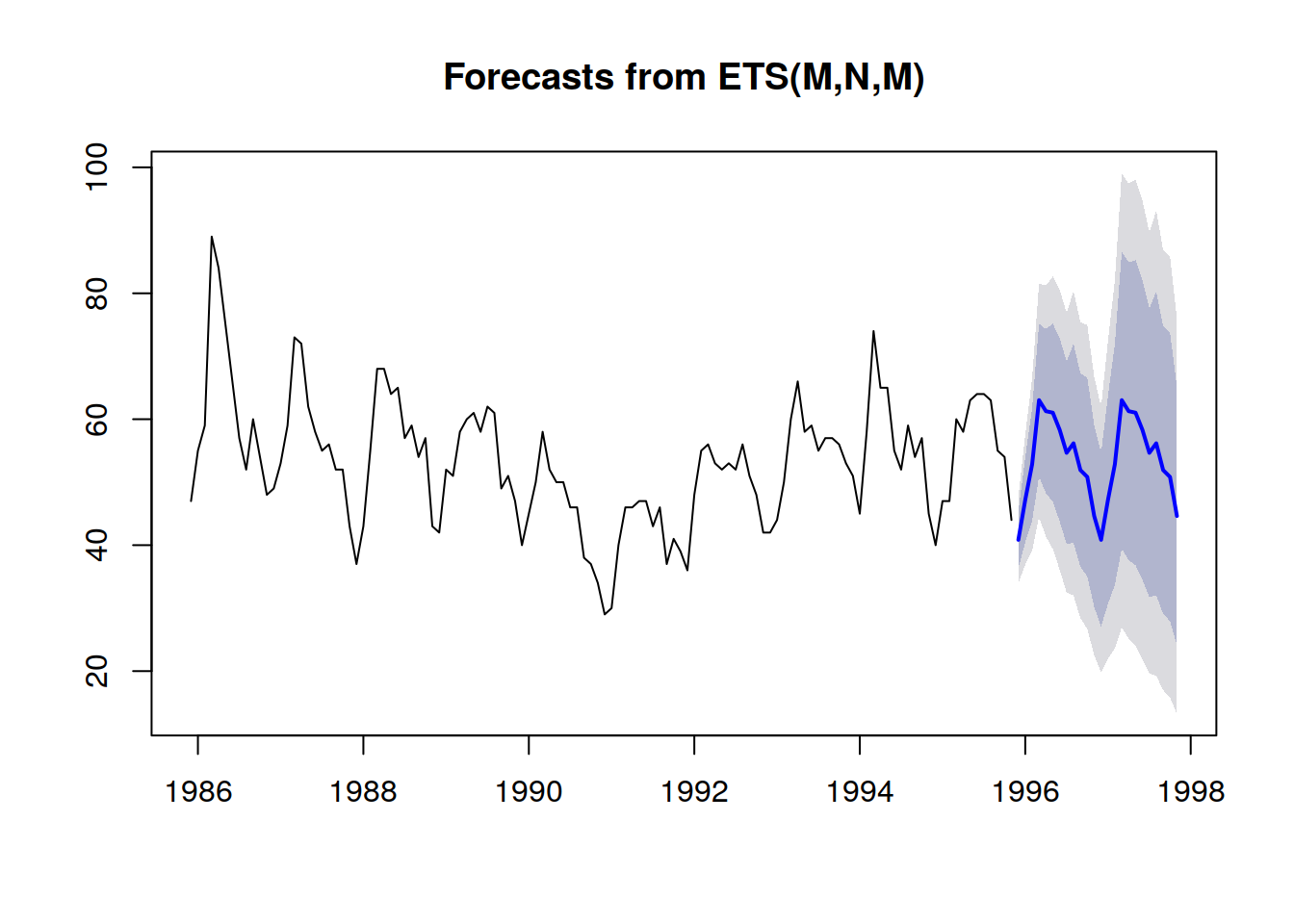
より良い表現、すなわち期間間の強い依存性を壊さない表現は、時間経過による累積値を参照し、それらの分位点を取り、さらに微分して各期間の増分を再現する方法です（本記事冒頭の確率論的予測の最初の図を参照）。可視化自体は同じですが、その根底にある意味は異なります。ここではシナリオごとの分位数を見て、非常に好ましい（または好ましくない）シナリオを示しています。

確率論的予測のアンチパターン

確率論的予測は、多くの人々が未来を「直感的に」考える方法に挑戦します。このセクションでは、確率論的予測に関して最も誤解されがちな側面のいくつかを取り上げます。

『予測不可能』な出来事というものは存在しない

決定論的な視点からは、宝くじの結果を予測することは不可能とされ、その理由は当たる確率が「100万分の1」であるからです。しかし、確率論的な視点からは、この問題は取るに足らないものです。すべてのチケットは「100万分の1」の勝率を持っています。結果の非常に高い分散は、現象そのものの「未知性」と混同されるべきではなく、宝くじの場合のように完全に理解可能です。確率論的予測は、分散を排除するのではなく、数量化し構造化することに関するものです。

『正規』分布というものは存在しない

正規分布（ガウス分布とも呼ばれる）は、サプライチェーンや物理学の教科書に遍在している。しかし、人間の事柄に関しては、ほとんど「通常分布」しているとは言えない。正規分布は、その設計上、平均から大きく逸脱する値を極めて稀なものとし、モデル上はありえない（すなわち十億分の一未満の確率）と見なされる。需要、リードタイム、返品などは、明確に正規分布していないパターンである。正規分布の唯一の利点は、学生向けの教科書問題として扱いやすく、明示的な解析解が得られる点にある。

確率のチェリーピッキング

確率分布に直面すると、その分布の一部分、例えば平均値や中央値を取り出して、それを基準に進めたくなる。しかし、このプロセスは、予測が本来持つ確率的側面の本質に反する。どの点を選んだとしても、それによって得られるのは莫大な情報の損失であるため、確率を単一の点推定に集約すべきではない。したがって、多少不都合ではあっても、確率は可能な限りそのまま保持されるべきである。なお、その集約の時点は、通常、将来の不確実性に直面しながらもリターンを最大化する最終的なサプライチェーンの意思決定時である。

統計的外れ値の除去

ほとんどの古典的な数値手法は—予測の決定論的観点に堅牢に基づいている（例：移動平均法）—統計的外れ値に遭遇すると著しく誤作動する。そのため、多くの企業は、過去のデータからこれらの外れ値を手動で「クリーン」するプロセスを確立している。しかし、このようなクレンジングプロセスの必要性は、むしろそれらの数値手法の欠点を浮き彫りにするに過ぎない。逆に、統計的外れ値は、分布のテール部で何が起こっているかをより正確に把握するための、確率的予測において不可欠な要素である。言い換えれば、これらの外れ値こそが、さらなる外れ値の発生確率を定量化する鍵となる。

銃撃戦に剣を持ち込む

確率分布を操作するには、専門のツールが必要である。確率的予測の作成は、企業に実際の価値を届けるための多くのステップの一つに過ぎない。適切なツールが欠如しているため、多くのサプライチェーン実務者は確率的予測を軽視してしまう。多くの企業向けソフトウェアベンダーもこの流れに乗り、「確率的予測」（「AI」や「ブロックチェーン」と併せて）をサポートしていると主張しているが、実際には数種類の確率モデルを化粧的に実装する程度にとどまっている（前述のセクション参照）。それらの数値結果を十分に活用するための大規模なツールがなければ、確率的予測モデルを提示してもほとんど意味がない。

注記